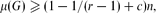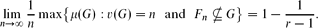Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
He, Bian
Jin, Ya-Lei
and
Zhang, Xiao-Dong
2013.
Sharp bounds for the signless Laplacian spectral radius in terms of clique number.
Linear Algebra and its Applications,
Vol. 438,
Issue. 10,
p.
3851.
Zhang, Minjie
and
Li, Shuchao
2015.
On the signless Laplacian spectra of k-trees.
Linear Algebra and its Applications,
Vol. 467,
Issue. ,
p.
136.
Li, Shuchao
and
Hu, Shuna
2016.
On the spectral moment of graphs with given clique number.
Rocky Mountain Journal of Mathematics,
Vol. 46,
Issue. 1,
Zhang, Minjie
and
Li, Shuchao
2016.
Extremal Halin graphs with respect to the signless Laplacian spectra.
Discrete Applied Mathematics,
Vol. 213,
Issue. ,
p.
207.
Zhang, Huihui
and
Li, Shuchao
2017.
On the Laplacian spectral radius of bipartite graphs with fixed order and size.
Discrete Applied Mathematics,
Vol. 229,
Issue. ,
p.
139.
Li, Binlong
and
Ning, Bo
2017.
Spectral analogues of Moon–Moser's theorem on Hamilton paths in bipartite graphs.
Linear Algebra and its Applications,
Vol. 515,
Issue. ,
p.
180.
Tait, Michael
and
Tobin, Josh
2017.
Three conjectures in extremal spectral graph theory.
Journal of Combinatorial Theory, Series B,
Vol. 126,
Issue. ,
p.
137.
Jin, Ya-Lei
and
Zhang, Xiao-Dong
2018.
The number of maximal cliques and spectral radius of graphs with certain forbidden subgraphs.
Discrete Mathematics, Algorithms and Applications,
Vol. 10,
Issue. 06,
p.
1850071.
Chen, Ming-Zhu
Liu, A-Ming
and
Zhang, Xiao-Dong
2019.
Spectral Extremal Results with Forbidding Linear Forests.
Graphs and Combinatorics,
Vol. 35,
Issue. 1,
p.
335.
Li, Yongtao
and
Peng, Yuejian
2022.
The spectral radius of graphs with no intersecting odd cycles.
Discrete Mathematics,
Vol. 345,
Issue. 8,
p.
112907.
Desai, Dheer Noal
Kang, Liying
Li, Yongtao
Ni, Zhenyu
Tait, Michael
and
Wang, Jing
2022.
Spectral extremal graphs for intersecting cliques.
Linear Algebra and its Applications,
Vol. 644,
Issue. ,
p.
234.
Gerbner, Dániel
and
Palmer, Cory
2022.
Some exact results for generalized Turán problems.
European Journal of Combinatorics,
Vol. 103,
Issue. ,
p.
103519.
Zhai, Mingqing
and
Lin, Huiqiu
2023.
A strengthening of the spectral chromatic critical edge theorem: Books and theta graphs.
Journal of Graph Theory,
Vol. 102,
Issue. 3,
p.
502.
Ai, Jiangdong
Im, Seonghyuk
Kim, Jaehoon
Lee, Hyunwoo
O, Suil
and
Zhang, Liwen
2024.
On the spectral radius of graphs with given maximum degree and girth.
Linear Algebra and its Applications,
Vol. 691,
Issue. ,
p.
182.
Li, Yongtao
Lu, Lu
and
Peng, Yuejian
2024.
A spectral Erdős-Rademacher theorem.
Advances in Applied Mathematics,
Vol. 158,
Issue. ,
p.
102720.
Chen, Ming-Zhu
Jin, Ya-Lei
and
Zhang, Peng-Li
2025.
The signless Laplacian spectral radius of book-free graphs.
Discrete Mathematics,
Vol. 348,
Issue. 7,
p.
114448.