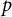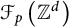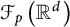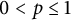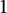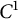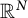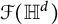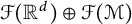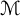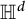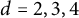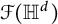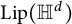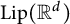1 Introduction
Given a metric space M with a distinguished point
![]() $0_M\in M$
, the Lipschitz-free space
$0_M\in M$
, the Lipschitz-free space
![]() $\mathcal {F}(M)$
, together with an isometric mapping
$\mathcal {F}(M)$
, together with an isometric mapping
![]() $\delta \colon M \to \mathcal {F}(M)$
, is the uniquely determined (up to linear isometry) Banach space with the following universal property: for every Lipschitz mapping
$\delta \colon M \to \mathcal {F}(M)$
, is the uniquely determined (up to linear isometry) Banach space with the following universal property: for every Lipschitz mapping
![]() $f\colon M \to X$
to a Banach space X with
$f\colon M \to X$
to a Banach space X with
![]() $f(0_M)=0$
, there is a unique bounded linear operator
$f(0_M)=0$
, there is a unique bounded linear operator
![]() $F\colon \mathcal {F}(M) \to X$
with
$F\colon \mathcal {F}(M) \to X$
with
![]() $\|F\| = \mathrm {Lip} (f)$
such that the diagram
$\|F\| = \mathrm {Lip} (f)$
such that the diagram

commutes. See, for instance, [Reference García-Sánchez, de Hevia and Tradacete26] for an approach to Lipschitz-free spaces via the universal property. The dual space of
![]() $\mathcal {F}(M)$
is the space
$\mathcal {F}(M)$
is the space
![]() $\mathrm {Lip}_0(M)$
of Lipschitz functions
$\mathrm {Lip}_0(M)$
of Lipschitz functions
![]() $f\colon M \to \mathbb {R}$
with
$f\colon M \to \mathbb {R}$
with
![]() $f(0_M)=0$
equipped with the Lipschitz constant as norm, (i.e.,
$f(0_M)=0$
equipped with the Lipschitz constant as norm, (i.e.,
![]() $\|f\|:=\mathrm {Lip} (f)$
). Note that the condition
$\|f\|:=\mathrm {Lip} (f)$
). Note that the condition
![]() $f(0_M)=0$
eliminates the constant functions and hence ensures that the Lipschitz constant is indeed a norm.
$f(0_M)=0$
eliminates the constant functions and hence ensures that the Lipschitz constant is indeed a norm.
The name Lipschitz-free spaces was introduced by G. Godefroy and N.J. Kalton in [Reference Godefroy and Kalton31] where, among others, these spaces are used to construct canonical examples of nonseparable Banach spaces which are bi-Lipschitz equivalent but not linearly isomorphic. Such spaces have been studied by several authors in different contexts and with different terminology, and we refer to [Reference Weaver47] and [Reference Ostrovska and Ostrovskii40, Section 1.6] for some terminological and historical remarks. The appearance of [Reference Godefroy and Kalton31] resulted in a new impetus to their study – in particular, in connection with nonlinear functional analysis, metric geometry, and theoretical computer science; let us refer to [Reference Albiac, Ansorena, Cúth and Doucha1, Reference Albiac, Ansorena, Cúth and Doucha2, Reference Aliaga, Gartland, Petitjean and Procházka4, Reference Aliaga, Pernecká, Petitjean and Procházka5, Reference Doucha and Kaufmann23, Reference Freeman and Gartland25, Reference Veeorg43, Reference Weaver46] for a nonexhaustive list of some recent results. Let us also refer to [Reference Godefroy29] for a recent nice survey on some aspects of the theory of Lipschitz-free spaces. A detailed exposition of the spaces
![]() $\mathrm {Lip}_0(M)$
and
$\mathrm {Lip}_0(M)$
and
![]() $\mathcal {F}(M)$
can also be found in N. Weaver’s book [Reference Weaver47]. There, in addition to the Banach space
$\mathcal {F}(M)$
can also be found in N. Weaver’s book [Reference Weaver47]. There, in addition to the Banach space
![]() $\mathrm {Lip}_0(M)$
, also the Banach space
$\mathrm {Lip}_0(M)$
, also the Banach space
![]() $\mathrm {Lip}(M)$
of bounded real-valued Lipschitz functions is introduced and studied in detail. This space has the additional important property to be a Banach algebra.
$\mathrm {Lip}(M)$
of bounded real-valued Lipschitz functions is introduced and studied in detail. This space has the additional important property to be a Banach algebra.
In metric geometry, up to dimension and a scaling of the metric, there only exist three model spaces (see, for example, [Reference Bridson and Haefliger14, Chapter I.2]): the sphere
![]() $\mathbb {S}^d$
with the intrinsic (geodesic) metric, the Euclidean space
$\mathbb {S}^d$
with the intrinsic (geodesic) metric, the Euclidean space
![]() $\mathbb {R}^d$
, and the hyperbolic space
$\mathbb {R}^d$
, and the hyperbolic space
![]() ${\mathbb {H}}^d$
. The structure of
${\mathbb {H}}^d$
. The structure of
![]() $\mathcal {F}(\mathbb {R}^d)$
is well studied, both from the isometric [Reference Cúth, Kalenda and Kaplický21] and from the isomorphic point of view [Reference Albiac, Ansorena, Cúth and Doucha3, Reference Borel-Mathurin13, Reference Cúth, Doucha and Wojtaszczyk20, Reference Hájek and Pernecká33, Reference Pernecká and Smith41]. Quite recently, it was proved that the spaces
$\mathcal {F}(\mathbb {R}^d)$
is well studied, both from the isometric [Reference Cúth, Kalenda and Kaplický21] and from the isomorphic point of view [Reference Albiac, Ansorena, Cúth and Doucha3, Reference Borel-Mathurin13, Reference Cúth, Doucha and Wojtaszczyk20, Reference Hájek and Pernecká33, Reference Pernecká and Smith41]. Quite recently, it was proved that the spaces
![]() $\mathcal {F}(\mathbb {S}^d)$
and
$\mathcal {F}(\mathbb {S}^d)$
and
![]() $\mathcal {F}(\mathbb {R}^d)$
are isomorphic, [Reference Albiac, Ansorena, Cúth and Doucha1, Theorem 4.21] (see also [Reference Freeman and Gartland25] for a more general result). However, much less seems to be known about the structure of the space
$\mathcal {F}(\mathbb {R}^d)$
are isomorphic, [Reference Albiac, Ansorena, Cúth and Doucha1, Theorem 4.21] (see also [Reference Freeman and Gartland25] for a more general result). However, much less seems to be known about the structure of the space
![]() $\mathcal {F}({\mathbb {H}}^d)$
and its dual space
$\mathcal {F}({\mathbb {H}}^d)$
and its dual space
![]() $\mathrm {Lip}_0({\mathbb {H}}^d)$
; some results concerning
$\mathrm {Lip}_0({\mathbb {H}}^d)$
; some results concerning
![]() $\mathcal {F}({\mathbb {H}}^d)$
can be found in [Reference Doucha and Kaufmann23] where, among others, the authors pose the questions of whether
$\mathcal {F}({\mathbb {H}}^d)$
can be found in [Reference Doucha and Kaufmann23] where, among others, the authors pose the questions of whether
![]() $\mathcal {F}(\mathbb {H}^{d})$
has a Schauder basis and whether it is isomorphic to
$\mathcal {F}(\mathbb {H}^{d})$
has a Schauder basis and whether it is isomorphic to
![]() $\mathcal {F}(\mathbb {R}^{d})$
. While our work was under review, the preprint [Reference Gartland27] by C. Gartland actually gave a positive answer to the latter question.
$\mathcal {F}(\mathbb {R}^{d})$
. While our work was under review, the preprint [Reference Gartland27] by C. Gartland actually gave a positive answer to the latter question.
The aim of this paper is to explain how the local structure of
![]() $\mathbb {H}^d$
for
$\mathbb {H}^d$
for
![]() $d=2,3,4$
together with a macroscopic view of
$d=2,3,4$
together with a macroscopic view of
![]() $\mathbb {H}^d$
determine the Banach space structure of
$\mathbb {H}^d$
determine the Banach space structure of
![]() $\mathcal {F}(\mathbb {H}^d)$
and
$\mathcal {F}(\mathbb {H}^d)$
and
![]() $\mathrm {Lip}_0(\mathbb {H}^d)$
. Since the space
$\mathrm {Lip}_0(\mathbb {H}^d)$
. Since the space
![]() $\mathrm {Lip}_0(\mathbb {H}^d)$
is more tangible than
$\mathrm {Lip}_0(\mathbb {H}^d)$
is more tangible than
![]() $\mathcal {F}(\mathbb {H}^d)$
, it will be more convenient for us to work with the space
$\mathcal {F}(\mathbb {H}^d)$
, it will be more convenient for us to work with the space
![]() $\mathrm {Lip}_0(\mathbb {H}^d)$
and then transfer the results to the predual. More precisely, we construct an (almost) explicit isomorphism
$\mathrm {Lip}_0(\mathbb {H}^d)$
and then transfer the results to the predual. More precisely, we construct an (almost) explicit isomorphism
where P is a polytope (with nonempty interior) in
![]() $\mathbb {R}^d$
and
$\mathbb {R}^d$
and
![]() $\mathcal {N}$
is a suitable net in
$\mathcal {N}$
is a suitable net in
![]() $\mathbb {H}^d$
. In particular, we build an explicit isomorphism between
$\mathbb {H}^d$
. In particular, we build an explicit isomorphism between
![]() $\mathrm {Lip}_0({\mathbb {H}}^d)$
and
$\mathrm {Lip}_0({\mathbb {H}}^d)$
and
![]() $Z \oplus \mathrm {Lip}_0(\mathcal {N})$
, where Z is a direct sum of certain subspaces of
$Z \oplus \mathrm {Lip}_0(\mathcal {N})$
, where Z is a direct sum of certain subspaces of
![]() $\mathrm {Lip}_0(P)$
. This gives us an explicit procedure to reduce the study of
$\mathrm {Lip}_0(P)$
. This gives us an explicit procedure to reduce the study of
![]() $\mathrm {Lip}_0({\mathbb {H}}^d)$
to the discrete case of
$\mathrm {Lip}_0({\mathbb {H}}^d)$
to the discrete case of
![]() $\mathrm {Lip}_0(\mathcal {N})$
and to a space of Lipschitz functions on
$\mathrm {Lip}_0(\mathcal {N})$
and to a space of Lipschitz functions on
![]() $\mathbb {R}^d$
. Since our main focus is on the hyperbolic case, we allow ourselves to use nonexplicit arguments, such as Lee–Naor extension results [Reference Lee and Naor39] and Pełczyński decomposition method, in the proof that Z is isomorphic to
$\mathbb {R}^d$
. Since our main focus is on the hyperbolic case, we allow ourselves to use nonexplicit arguments, such as Lee–Naor extension results [Reference Lee and Naor39] and Pełczyński decomposition method, in the proof that Z is isomorphic to
![]() $\mathrm {Lip}_0(P)$
(in Section 4). Let us, however, point out that this part of the argument could also be made entirely explicit by using a variant of the arguments from Section 5.
$\mathrm {Lip}_0(P)$
(in Section 4). Let us, however, point out that this part of the argument could also be made entirely explicit by using a variant of the arguments from Section 5.
Since
![]() $\Phi $
is weak
$\Phi $
is weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous, it is the adjoint of an isomorphism
$^*$
continuous, it is the adjoint of an isomorphism
Moreover, by the results of [Reference Cúth, Kalenda and Kaplický21],
![]() $\mathcal {F}(P)$
is isomorphic to
$\mathcal {F}(P)$
is isomorphic to
![]() $\mathcal {F}(\mathbb {R}^{d})$
, which yields
$\mathcal {F}(\mathbb {R}^{d})$
, which yields
for
![]() $d=2,3,4$
. Since both the space
$d=2,3,4$
. Since both the space
![]() $\mathcal {F}(\mathbb {R}^d)$
and
$\mathcal {F}(\mathbb {R}^d)$
and
![]() $\mathcal {F}(\mathcal {N})$
have a Schauder basis, the former result being due to P. Hájek and E. Pernecká in [Reference Hájek and Pernecká33] and the latter to M. Doucha and P. Kaufmann in [Reference Doucha and Kaufmann23], we conclude that, for
$\mathcal {F}(\mathcal {N})$
have a Schauder basis, the former result being due to P. Hájek and E. Pernecká in [Reference Hájek and Pernecká33] and the latter to M. Doucha and P. Kaufmann in [Reference Doucha and Kaufmann23], we conclude that, for
![]() $d=2,3,4$
,
$d=2,3,4$
,
![]() $\mathcal {F}({\mathbb {H}}^d)$
also admits a Schauder basis, thereby giving a partial positive answer to the first question mentioned above. Let us recall that if one is aiming for weaker structural properties, such as the bounded approximation property, or the
$\mathcal {F}({\mathbb {H}}^d)$
also admits a Schauder basis, thereby giving a partial positive answer to the first question mentioned above. Let us recall that if one is aiming for weaker structural properties, such as the bounded approximation property, or the
![]() $(\pi )$
-property, then more general results are available; see, for instance, [Reference Godefroy30, Reference Lancien and Pernecká37] and the references therein.
$(\pi )$
-property, then more general results are available; see, for instance, [Reference Godefroy30, Reference Lancien and Pernecká37] and the references therein.
Using the same methods, we also show that the space
![]() $\mathrm {Lip}(\mathbb {H}^d)$
is isomorphic to
$\mathrm {Lip}(\mathbb {H}^d)$
is isomorphic to
![]() $\mathrm {Lip}(\mathbb {R}^d)$
, this time by giving an entirely explicit isomorphism (Remark 5.11). Combining this result with standard arguments, in Remark 5.12, we conclude that
$\mathrm {Lip}(\mathbb {R}^d)$
, this time by giving an entirely explicit isomorphism (Remark 5.11). Combining this result with standard arguments, in Remark 5.12, we conclude that
(i.e., the spaces of bounded Lipschitz functions on the model spaces of metric geometry are all isomorphic).
At the core of our argument, we have to decompose a Lipschitz function on
![]() $\mathbb {H}^d$
into a Lipschitz function on a net
$\mathbb {H}^d$
into a Lipschitz function on a net
![]() $\mathcal {N}$
and a sequence of Lipschitz functions on a convex subset of
$\mathcal {N}$
and a sequence of Lipschitz functions on a convex subset of
![]() $\mathbb {H}^d$
. In order to do this, we consider a suitable tiling of
$\mathbb {H}^d$
. In order to do this, we consider a suitable tiling of
![]() $\mathbb {H}^d$
by polytopes; the existence of such tilings depends upon classical results from the theory of reflection groups; see, for example, [Reference Davis22, Chapter 6] or [Reference Vinberg and Shvartsman45, Chapter 5]. More precisely, given a right-angled polytope P (namely, such that all dihedral angles are exactly
$\mathbb {H}^d$
by polytopes; the existence of such tilings depends upon classical results from the theory of reflection groups; see, for example, [Reference Davis22, Chapter 6] or [Reference Vinberg and Shvartsman45, Chapter 5]. More precisely, given a right-angled polytope P (namely, such that all dihedral angles are exactly
![]() $\pi /2$
), by reflecting across the faces of P, we obtain a tessellation of
$\pi /2$
), by reflecting across the faces of P, we obtain a tessellation of
![]() $\mathbb {H}^d$
by isometric copies of P. In [Reference Vinberg44] (see also [Reference Potyagailo and Vinberg42, Section 2]), the author shows that such right-angled polytopes exist only if
$\mathbb {H}^d$
by isometric copies of P. In [Reference Vinberg44] (see also [Reference Potyagailo and Vinberg42, Section 2]), the author shows that such right-angled polytopes exist only if
![]() $d\leqslant 4$
; explicit constructions in dimensions
$d\leqslant 4$
; explicit constructions in dimensions
![]() $d=2,3,4$
were already known to exist (see Section 3.1). This justifies why we are able to prove our results only in dimension
$d=2,3,4$
were already known to exist (see Section 3.1). This justifies why we are able to prove our results only in dimension
![]() $d=2,3,4$
. In order to emphasize the subtlety of hyperbolic tilings results, let us mention two more results: in dimension
$d=2,3,4$
. In order to emphasize the subtlety of hyperbolic tilings results, let us mention two more results: in dimension
![]() $d\geqslant 6$
, there exists no regular tiling of
$d\geqslant 6$
, there exists no regular tiling of
![]() ${\mathbb {H}}^d$
[Reference Coxeter19, p. 206], and, more generally, for
${\mathbb {H}}^d$
[Reference Coxeter19, p. 206], and, more generally, for
![]() $d\geqslant 30$
, there are no hyperbolic reflection groups at all (see, for example, [Reference Davis22, Theorem 6.11.8]).
$d\geqslant 30$
, there are no hyperbolic reflection groups at all (see, for example, [Reference Davis22, Theorem 6.11.8]).
Given a tiling of
![]() ${\mathbb {H}}^d$
by right-angled polytopes, we first use an extension operator from the net, given by choosing a distinguished point inside the polytope, to decompose a
${\mathbb {H}}^d$
by right-angled polytopes, we first use an extension operator from the net, given by choosing a distinguished point inside the polytope, to decompose a
![]() $\mathrm {Lip}_0$
-function on
$\mathrm {Lip}_0$
-function on
![]() ${\mathbb {H}}^d$
into a function on the net and a bounded Lipschitz function on
${\mathbb {H}}^d$
into a function on the net and a bounded Lipschitz function on
![]() ${\mathbb {H}}^d$
. Then, using an extension operator for Lipschitz functions on P, we decompose the bounded Lipschitz function in a bounded sequence of Lipschitz functions on P. The latter construction is inspired by a decomposition method for (
${\mathbb {H}}^d$
. Then, using an extension operator for Lipschitz functions on P, we decompose the bounded Lipschitz function in a bounded sequence of Lipschitz functions on P. The latter construction is inspired by a decomposition method for (
![]() $C^\infty $
-)smooth functions on
$C^\infty $
-)smooth functions on
![]() $\mathbb {R}^d$
into sequences of functions on the unit cube in [Reference Bargetz8] and [Reference Bargetz9].
$\mathbb {R}^d$
into sequences of functions on the unit cube in [Reference Bargetz8] and [Reference Bargetz9].
Let us close this section with a brief description of the structure of the paper. In Section 2, we recall basic notions on Lipschitz-free spaces and metric geometry. A self-contained revision of hyperbolic geometry is the content of Section 3; in particular, we explain the properties of the tilings that we need in Section 3.1. As we mentioned already, Section 4 is dedicated to the local problem, and we study the space
![]() $\mathrm {Lip}_0(P)$
, for a polytope P in
$\mathrm {Lip}_0(P)$
, for a polytope P in
![]() $\mathbb {R}^d$
. Finally, the core of our paper with the proof of the main results is Section 5.
$\mathbb {R}^d$
. Finally, the core of our paper with the proof of the main results is Section 5.
2 Preliminary material
Given a pointed metric space
![]() $(M,d)$
with distinguished point
$(M,d)$
with distinguished point
![]() $0_M\in M$
, we consider the Banach space
$0_M\in M$
, we consider the Banach space
![]() $\mathrm {Lip}_0(M)$
of all Lipschitz functions
$\mathrm {Lip}_0(M)$
of all Lipschitz functions
![]() $f\colon M\to \mathbb {R}$
such that
$f\colon M\to \mathbb {R}$
such that
![]() $f(0_M)=0$
, endowed with the norm
$f(0_M)=0$
, endowed with the norm

Moreover, when
![]() $(M,d)$
is a metric space, we consider the vector space of all bounded Lipschitz functions
$(M,d)$
is a metric space, we consider the vector space of all bounded Lipschitz functions
![]() $f\colon M\to \mathbb {R}$
that, following [Reference Weaver47, Chapter 2], we denote by
$f\colon M\to \mathbb {R}$
that, following [Reference Weaver47, Chapter 2], we denote by
![]() $\mathrm {Lip}(M)$
.
$\mathrm {Lip}(M)$
.
![]() $\mathrm {Lip}(M)$
becomes a Banach space when equipped with the norm
$\mathrm {Lip}(M)$
becomes a Banach space when equipped with the norm
The pointwise multiplication induces an algebra structure on
![]() $\mathrm {Lip}(M)$
due to the basic inequality
$\mathrm {Lip}(M)$
due to the basic inequality
When M is bounded, the same product also gives an algebra structure on
![]() $\mathrm {Lip}_0(M)$
because
$\mathrm {Lip}_0(M)$
because
![]() $\|f\|_\infty \leqslant \operatorname {diam}(M) \|f\|_{\mathrm {Lip}_0}$
. Actually, a different product turns every
$\|f\|_\infty \leqslant \operatorname {diam}(M) \|f\|_{\mathrm {Lip}_0}$
. Actually, a different product turns every
![]() $\mathrm {Lip}_0(M)$
into a Banach algebra, [Reference Albiac, Ansorena, Cúth and Doucha2].
$\mathrm {Lip}_0(M)$
into a Banach algebra, [Reference Albiac, Ansorena, Cúth and Doucha2].
For
![]() $p\in M$
, the evaluation functional
$p\in M$
, the evaluation functional
![]() $\delta _p\in \mathrm {Lip}_0(M)^*$
is defined by
$\delta _p\in \mathrm {Lip}_0(M)^*$
is defined by ![]() . It is easy to see that
. It is easy to see that
![]() $\|\delta _p\|= d(p,0_M)$
. Then one can define
$\|\delta _p\|= d(p,0_M)$
. Then one can define ![]() and verify that
and verify that
![]() $\mathcal {F}(M)$
satisfies the universal property stated in the Introduction. In particular,
$\mathcal {F}(M)$
satisfies the universal property stated in the Introduction. In particular,
![]() $\mathcal {F}(M)^*=\mathrm {Lip}_0(M)$
.
$\mathcal {F}(M)^*=\mathrm {Lip}_0(M)$
.
As mentioned in the Introduction, our argument will proceed in
![]() $\mathrm {Lip}_0(M)$
, and only at the very end, we will pass to preduals and deduce results for
$\mathrm {Lip}_0(M)$
, and only at the very end, we will pass to preduals and deduce results for
![]() $\mathcal {F}(M)$
. Therefore, we need information on the weak
$\mathcal {F}(M)$
. Therefore, we need information on the weak
![]() $^*$
topology of
$^*$
topology of
![]() $\mathrm {Lip}_0(M)$
induced by the predual
$\mathrm {Lip}_0(M)$
induced by the predual
![]() $\mathcal {F}(M)$
. By definition, the set
$\mathcal {F}(M)$
. By definition, the set
![]() $\{\delta _p\colon p\in M\}$
of elementary molecules is linearly dense in
$\{\delta _p\colon p\in M\}$
of elementary molecules is linearly dense in
![]() $\mathcal {F}(M)$
. Thus, on bounded sets, the weak
$\mathcal {F}(M)$
. Thus, on bounded sets, the weak
![]() $^*$
topology coincides with the weak topology induced by the functionals
$^*$
topology coincides with the weak topology induced by the functionals
![]() $\{\delta _p \colon p\in M\}$
. In other words, it agrees with the topology of pointwise convergence on M. When combined with the Banach–Dieudonné theorem, this fact has important consequences. First, a subspace
$\{\delta _p \colon p\in M\}$
. In other words, it agrees with the topology of pointwise convergence on M. When combined with the Banach–Dieudonné theorem, this fact has important consequences. First, a subspace
![]() $X\subset \mathrm {Lip}_0(M)$
is weak
$X\subset \mathrm {Lip}_0(M)$
is weak
![]() $^*$
closed if and only if it is pointwise closed. Second, a bounded operator
$^*$
closed if and only if it is pointwise closed. Second, a bounded operator
![]() $L\colon \mathrm {Lip}_0(M)\to \mathrm {Lip}_0(N)$
is weak
$L\colon \mathrm {Lip}_0(M)\to \mathrm {Lip}_0(N)$
is weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous if and only if it is pointwise-to-pointwise continuous (see, for example. [Reference Fabian, Habala, Hájek, Montesinos Santalucía and Zizler24, Exercise 3.65] or [Reference Weaver47, Corollary 2.33]). These facts will be freely used multiple times in our arguments. Moreover, if X is a weak
$^*$
continuous if and only if it is pointwise-to-pointwise continuous (see, for example. [Reference Fabian, Habala, Hájek, Montesinos Santalucía and Zizler24, Exercise 3.65] or [Reference Weaver47, Corollary 2.33]). These facts will be freely used multiple times in our arguments. Moreover, if X is a weak
![]() $^*$
closed subspace of
$^*$
closed subspace of
![]() $\mathrm {Lip}_0(M)$
, then it is the dual to some quotient Z of
$\mathrm {Lip}_0(M)$
, then it is the dual to some quotient Z of
![]() $\mathcal {F}(M)$
, and the weak
$\mathcal {F}(M)$
, and the weak
![]() $^*$
topology of X induced by Z coincides with the restriction to X of the weak
$^*$
topology of X induced by Z coincides with the restriction to X of the weak
![]() $^*$
topology of
$^*$
topology of
![]() $\mathrm {Lip}_0(M)$
; see, for example, [Reference Conway18, Corollary V.2.2].
$\mathrm {Lip}_0(M)$
; see, for example, [Reference Conway18, Corollary V.2.2].
A ubiquitous role in our proofs will be played by linear extension operators. If N is a subset of M with
![]() $0_M\in N$
, a linear extension operator
$0_M\in N$
, a linear extension operator
![]() $E\colon \mathrm {Lip}_0(N)\to \mathrm {Lip}_0(M)$
is a linear operator such that
$E\colon \mathrm {Lip}_0(N)\to \mathrm {Lip}_0(M)$
is a linear operator such that
![]() $Ef$
is an extension of f for every
$Ef$
is an extension of f for every
![]() $f\in \mathrm {Lip}_0(N)$
. Plainly, the restriction operator
$f\in \mathrm {Lip}_0(N)$
. Plainly, the restriction operator
![]() $f\mapsto f|_N$
is a left-inverse to E. Thus, E defines an isomorphic embedding of
$f\mapsto f|_N$
is a left-inverse to E. Thus, E defines an isomorphic embedding of
![]() $\mathrm {Lip}_0(N)$
as a complemented subspace of
$\mathrm {Lip}_0(N)$
as a complemented subspace of
![]() $\mathrm {Lip}_0(M)$
. Moreover, if E is pointwise-to-pointwise continuous, both the isomorphic embedding and the projection are weak
$\mathrm {Lip}_0(M)$
. Moreover, if E is pointwise-to-pointwise continuous, both the isomorphic embedding and the projection are weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous. The construction of linear extension operators for Lipschitz functions has been a topic of great interest in recent years; see, for example, [Reference Albiac, Ansorena, Cúth and Doucha1, Reference Ambrosio and Puglisi6, Reference Brudnyi and Brudnyi15, Reference Bruè, Di Marino and Stra16, Reference Godefroy28, Reference Johnson, Lindenstrauss and Schechtman35, Reference Lee and Naor39].
$^*$
continuous. The construction of linear extension operators for Lipschitz functions has been a topic of great interest in recent years; see, for example, [Reference Albiac, Ansorena, Cúth and Doucha1, Reference Ambrosio and Puglisi6, Reference Brudnyi and Brudnyi15, Reference Bruè, Di Marino and Stra16, Reference Godefroy28, Reference Johnson, Lindenstrauss and Schechtman35, Reference Lee and Naor39].
In most cases, our extensions operators will be based on direct and explicit constructions. However, in one place we shall use the following deep extension result due to Lee and Naor [Reference Lee and Naor39]: there is a universal constant C such that for every pointed metric space
![]() $(M,d)$
and every subspace N with
$(M,d)$
and every subspace N with
![]() $0_M\in N$
that is
$0_M\in N$
that is
![]() $\lambda $
-doubling, there is a linear extension operator
$\lambda $
-doubling, there is a linear extension operator
![]() $E\colon \mathrm {Lip}_0(N)\to \mathrm {Lip}_0(M)$
with
$E\colon \mathrm {Lip}_0(N)\to \mathrm {Lip}_0(M)$
with
![]() $\|E\|\leqslant C\log (\lambda )$
. For a more recent simpler proof, see [Reference Bruè, Di Marino and Stra16, Theorem 4.1]; importantly, the operator E is also weak
$\|E\|\leqslant C\log (\lambda )$
. For a more recent simpler proof, see [Reference Bruè, Di Marino and Stra16, Theorem 4.1]; importantly, the operator E is also weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous, as it is explained for example in [Reference Lancien and Pernecká37].
$^*$
continuous, as it is explained for example in [Reference Lancien and Pernecká37].
Next, we need to mention some basics on metric geometry. Recall that a metric space
![]() $(M,d)$
is geodesic if for every two points
$(M,d)$
is geodesic if for every two points
![]() $x,y\in M$
, there is an isometry
$x,y\in M$
, there is an isometry
![]() $\gamma \colon [0,d(x,y)]\to M$
such that
$\gamma \colon [0,d(x,y)]\to M$
such that
![]() $\gamma (0)=x$
and
$\gamma (0)=x$
and
![]() $\gamma (d(x,y))=y$
. In case such an isometry
$\gamma (d(x,y))=y$
. In case such an isometry
![]() $\gamma $
is unique,
$\gamma $
is unique,
![]() $(M,d)$
is said to be uniquely geodesic. Intuitively speaking, geodesics are the metric analogue of segments. Accordingly, the image
$(M,d)$
is said to be uniquely geodesic. Intuitively speaking, geodesics are the metric analogue of segments. Accordingly, the image
![]() $\gamma ([0,d(x,y)])$
of a geodesic connecting x to y is sometimes called metric segment and denoted
$\gamma ([0,d(x,y)])$
of a geodesic connecting x to y is sometimes called metric segment and denoted
![]() $[xy]$
. Moreover, we say that a subset C of M is (geodesically) convex if every metric segment
$[xy]$
. Moreover, we say that a subset C of M is (geodesically) convex if every metric segment
![]() $[xy]$
with
$[xy]$
with
![]() $x,y\in C$
is entirely contained in C. Let us refer, for example, to [Reference Bridson and Haefliger14] for more on geodesic metric spaces.
$x,y\in C$
is entirely contained in C. Let us refer, for example, to [Reference Bridson and Haefliger14] for more on geodesic metric spaces.
An important property of geodesic metric spaces is that the Lipschitz condition becomes a local property, in the sense of the following lemma. For convex subsets of Banach spaces, it is due to D. J. Ives and D. Preiss in [Reference Ives and Preiss34].
Lemma 2.1 [Reference Bargetz, Reich and Thimm10, Lemma 2.1]
Let M be a geodesic space, N a metric space, and
![]() $\{Z_i\}_{i=1}^{\infty }$
a countable family of sets covering M. Let
$\{Z_i\}_{i=1}^{\infty }$
a countable family of sets covering M. Let
![]() $f\colon M\to N$
be a continuous mapping whose restrictions to the sets
$f\colon M\to N$
be a continuous mapping whose restrictions to the sets
![]() $Z_i$
are Lipschitz and satisfy
$Z_i$
are Lipschitz and satisfy
![]() $\mathrm {Lip}(f|_{Z_i})\leqslant L$
for some
$\mathrm {Lip}(f|_{Z_i})\leqslant L$
for some
![]() $L>0$
. Then f is Lipschitz with
$L>0$
. Then f is Lipschitz with
![]() $\mathrm {Lip}(f) \leqslant L$
.
$\mathrm {Lip}(f) \leqslant L$
.
3 Hyperbolic geometry
This section is dedicated to a brief introduction to the hyperbolic d-space
![]() ${\mathbb {H}}^d$
. The shortest way to introduce it is to define
${\mathbb {H}}^d$
. The shortest way to introduce it is to define
![]() ${\mathbb {H}}^d$
as the unique complete, simply-connected Riemannian d-manifold with constant sectional curvature
${\mathbb {H}}^d$
as the unique complete, simply-connected Riemannian d-manifold with constant sectional curvature
![]() $-1$
. The uniqueness of a Riemannian d-manifold with such properties is a consequence of the Killing–Hopf theorem; see, for example, [Reference Lee38, Theorem 12.4]. However, for our purposes, it will be more convenient to have an explicit description of a model for
$-1$
. The uniqueness of a Riemannian d-manifold with such properties is a consequence of the Killing–Hopf theorem; see, for example, [Reference Lee38, Theorem 12.4]. However, for our purposes, it will be more convenient to have an explicit description of a model for
![]() ${\mathbb {H}}^d$
; we shall now recall two such models and later use whichever model is more convenient for our purpose.
${\mathbb {H}}^d$
; we shall now recall two such models and later use whichever model is more convenient for our purpose.
Let us start by recalling the hyperboloid model: consider the non-degenerate bilinear form

on
![]() $\mathbb {R}^{d+1}$
and define
$\mathbb {R}^{d+1}$
and define
A metric on
![]() ${\mathbb {H}}^d$
can be defined by
${\mathbb {H}}^d$
can be defined by
As it turns out,
![]() $\langle \cdot ,\cdot \rangle $
is positive definite on the tangent bundle of
$\langle \cdot ,\cdot \rangle $
is positive definite on the tangent bundle of
![]() ${\mathbb {H}}^d$
and
${\mathbb {H}}^d$
and
![]() $\rho $
is exactly the Riemannian distance induced by the Riemannian metric
$\rho $
is exactly the Riemannian distance induced by the Riemannian metric
![]() $\langle \cdot ,\cdot \rangle $
on
$\langle \cdot ,\cdot \rangle $
on
![]() ${\mathbb {H}}^d$
. Geodesic lines are defined as the intersections of
${\mathbb {H}}^d$
. Geodesic lines are defined as the intersections of
![]() ${\mathbb {H}}^d$
with
${\mathbb {H}}^d$
with
![]() $2$
-dimensional subspaces of
$2$
-dimensional subspaces of
![]() $\mathbb {R}^{d+1}$
. In particular,
$\mathbb {R}^{d+1}$
. In particular,
![]() ${\mathbb {H}}^d$
is uniquely geodesic, and every geodesic can be uniquely extended to a geodesic line. Angles are also defined in terms of
${\mathbb {H}}^d$
is uniquely geodesic, and every geodesic can be uniquely extended to a geodesic line. Angles are also defined in terms of
![]() $\langle \cdot ,\cdot \rangle $
: given two geodesics that meet at a point
$\langle \cdot ,\cdot \rangle $
: given two geodesics that meet at a point
![]() $\xi \in {\mathbb {H}}^d$
, one takes unit tangent vectors u and v to the geodesics at
$\xi \in {\mathbb {H}}^d$
, one takes unit tangent vectors u and v to the geodesics at
![]() $\xi $
and defines the angle between the geodesics as the unique
$\xi $
and defines the angle between the geodesics as the unique
![]() $\alpha \in [0,\pi ]$
such that
$\alpha \in [0,\pi ]$
such that
![]() $\cos \alpha = \langle u,v\rangle $
. Note that, in particular, if the point in question is the origin, then
$\cos \alpha = \langle u,v\rangle $
. Note that, in particular, if the point in question is the origin, then
![]() $u_{d+1}v_{d+1}=0$
; thus,
$u_{d+1}v_{d+1}=0$
; thus,
![]() $\langle u,v\rangle _{{\mathbb {H}}^d}=\langle u,v\rangle _{\mathbb {R}^{d+1}}$
, and hence, the angle is the Euclidean one. For the same reason, if any geodesic subspace containing the origin meets a geodesic at an orthogonal angle in
$\langle u,v\rangle _{{\mathbb {H}}^d}=\langle u,v\rangle _{\mathbb {R}^{d+1}}$
, and hence, the angle is the Euclidean one. For the same reason, if any geodesic subspace containing the origin meets a geodesic at an orthogonal angle in
![]() $\mathbb {R}^{d+1}$
, then the (two possible) tangent vectors u of said geodesic will satisfy
$\mathbb {R}^{d+1}$
, then the (two possible) tangent vectors u of said geodesic will satisfy
![]() $u_{d+1}=0$
, and the hyperbolic angle will be orthogonal as well.
$u_{d+1}=0$
, and the hyperbolic angle will be orthogonal as well.
An isometry of
![]() ${\mathbb {H}}^d$
is a bijection of
${\mathbb {H}}^d$
is a bijection of
![]() ${\mathbb {H}}^d$
that preserves the distance
${\mathbb {H}}^d$
that preserves the distance
![]() $\rho $
; it then follows that such isometries also preserve angles. Let us recall that the group of isometries acts transitively on
$\rho $
; it then follows that such isometries also preserve angles. Let us recall that the group of isometries acts transitively on
![]() ${\mathbb {H}}^d$
; moreover, each isometry of
${\mathbb {H}}^d$
; moreover, each isometry of
![]() ${\mathbb {H}}^d$
can be obtained as a composition of at most
${\mathbb {H}}^d$
can be obtained as a composition of at most
![]() $d+1$
reflections through hyperplanes. More on isometries of
$d+1$
reflections through hyperplanes. More on isometries of
![]() ${\mathbb {H}}^d$
can be found in [Reference Berger11, Chapter 19], [Reference Bridson and Haefliger14, Chapter I.2], or [Reference Cannon, Floyd, Kenyon and Parry17, Section 10].
${\mathbb {H}}^d$
can be found in [Reference Berger11, Chapter 19], [Reference Bridson and Haefliger14, Chapter I.2], or [Reference Cannon, Floyd, Kenyon and Parry17, Section 10].
We next briefly describe the Beltrami–Klein model. It is represented by points in the Euclidean open unit ball ![]() . Geodesics are simply intersections of Euclidean lines with
. Geodesics are simply intersections of Euclidean lines with
![]() $\mathbb {B}^d$
. Likewise, hyperplanes are intersections of Euclidean hyperplanes with
$\mathbb {B}^d$
. Likewise, hyperplanes are intersections of Euclidean hyperplanes with
![]() $\mathbb {B}^d$
. The metric for
$\mathbb {B}^d$
. The metric for
![]() ${\mathbb {H}}^d_{BK}$
can be defined as follows: given points x and y in
${\mathbb {H}}^d_{BK}$
can be defined as follows: given points x and y in
![]() $\mathbb {B}^d$
, let
$\mathbb {B}^d$
, let
![]() $x_\infty $
and
$x_\infty $
and
![]() $y_\infty $
be the intersections of the line through x and y with the boundary of
$y_\infty $
be the intersections of the line through x and y with the boundary of
![]() $\mathbb {B}^d$
(arranged so that
$\mathbb {B}^d$
(arranged so that
![]() $x_\infty ,x,y,y_\infty $
appear in order). Then
$x_\infty ,x,y,y_\infty $
appear in order). Then

Further information on this and more models can be found in [Reference Berger11, Chapter 19], or [Reference Bridson and Haefliger14, Chapter I.6]. Let us notice that, by the Killing–Hopf theorem, all such models are mutually isometric. More importantly, simple and explicit isometries between the models are available, thus allowing explicit transfer of properties; see, for example, [Reference Berger11, Chapter 19], or [Reference Lee38, Theorem 3.7]. Finally, for a gentle and elementary introduction to hyperbolic geometry, mainly in the plane, we refer the interested reader to [Reference Anderson7].
The last result we require is a particular case of the well-known fact from Riemannian geometry that differentiable maps between Riemannian manifolds are locally Lipschitz. A direct, computational proof of this particular case can be given by using the explicit formula for the metric.
Lemma 3.1 Let
![]() ${\mathbb {H}}^d_{BK}$
be the Beltrami-Klein model of
${\mathbb {H}}^d_{BK}$
be the Beltrami-Klein model of
![]() ${\mathbb {H}}^d$
and let
${\mathbb {H}}^d$
and let
![]() $\mathbb {B}^d$
be the Euclidean open unit ball in
$\mathbb {B}^d$
be the Euclidean open unit ball in
![]() $\mathbb {R}^d$
. Then the identity function
$\mathbb {R}^d$
. Then the identity function
![]() $\mathrm {id}\colon {\mathbb {H}}^d_{BK} \to \mathbb {B}^d$
is locally bi-Lipschitz.
$\mathrm {id}\colon {\mathbb {H}}^d_{BK} \to \mathbb {B}^d$
is locally bi-Lipschitz.
3.1 Tilings of
 ${\mathbb {H}}^d$
${\mathbb {H}}^d$
We call a subset of
![]() $\mathbb {R}^d$
or
$\mathbb {R}^d$
or
![]() ${\mathbb {H}}^d$
a polyhedron if it is a finite intersection of closed half-spaces. A bounded (or equivalently compact) polyhedron is called a polytope. Note that polyhedra are convex sets, as is, for example, obvious in the Beltrami–Klein model. Hence, the nearest point projection – namely, the mapping which assigns to a point x the point in the polyhedron which minimizes the distance to x – is well defined and
${\mathbb {H}}^d$
a polyhedron if it is a finite intersection of closed half-spaces. A bounded (or equivalently compact) polyhedron is called a polytope. Note that polyhedra are convex sets, as is, for example, obvious in the Beltrami–Klein model. Hence, the nearest point projection – namely, the mapping which assigns to a point x the point in the polyhedron which minimizes the distance to x – is well defined and
![]() $1$
-Lipschitz; see Proposition 2.4 in [Reference Bridson and Haefliger14, p. 176]. In particular, polyhedra are
$1$
-Lipschitz; see Proposition 2.4 in [Reference Bridson and Haefliger14, p. 176]. In particular, polyhedra are
![]() $1$
-Lipschitz retracts of both
$1$
-Lipschitz retracts of both
![]() $\mathbb {R}^d$
and
$\mathbb {R}^d$
and
![]() ${\mathbb {H}}^d$
.
${\mathbb {H}}^d$
.
In order to investigate the local and global structure of the Lipschitz functions on
![]() ${\mathbb {H}}^d$
separately, we will need a suitable tiling of the hyperbolic space
${\mathbb {H}}^d$
separately, we will need a suitable tiling of the hyperbolic space
![]() ${\mathbb {H}}^d$
. A sequence
${\mathbb {H}}^d$
. A sequence
![]() $(P_n)_{n\in \mathbb {N}}$
of polytopes is a tiling, or tessellation, of
$(P_n)_{n\in \mathbb {N}}$
of polytopes is a tiling, or tessellation, of
![]() ${\mathbb {H}}^d$
if
${\mathbb {H}}^d$
if
![]() $\bigcup _{n\in \mathbb {N}}P_n= {\mathbb {H}}^d$
, and the intersection of any two distinct polytopes is either empty or a face of both polytopes (in particular, the interiors of the polytopes
$\bigcup _{n\in \mathbb {N}}P_n= {\mathbb {H}}^d$
, and the intersection of any two distinct polytopes is either empty or a face of both polytopes (in particular, the interiors of the polytopes
![]() $P_n$
are mutually disjoint).
$P_n$
are mutually disjoint).
In our arguments, we will use the existence in
![]() ${\mathbb {H}}^d$
for
${\mathbb {H}}^d$
for
![]() $d=2,3,4$
of a regular orthogonal tiling – namely, a tiling
$d=2,3,4$
of a regular orthogonal tiling – namely, a tiling
![]() $(P_n)_{n\in \mathbb {N}}$
consisting of mutually isometric polytopes and where each
$(P_n)_{n\in \mathbb {N}}$
consisting of mutually isometric polytopes and where each
![]() $P_n$
satisfies the following definitions (see, for example, [Reference Davis22, Chapter 6] for more details):
$P_n$
satisfies the following definitions (see, for example, [Reference Davis22, Chapter 6] for more details):
-
(T1) A polytope P in
 ${\mathbb {H}}^d$
is regular if the group of isometries of P is flag-transitive. More precisely, a flag in P is a chain
${\mathbb {H}}^d$
is regular if the group of isometries of P is flag-transitive. More precisely, a flag in P is a chain
 $F_0\subset F_1\subset \dots \subset F_{d-1}$
, where
$F_0\subset F_1\subset \dots \subset F_{d-1}$
, where
 $F_0$
is a vertex of P and each
$F_0$
is a vertex of P and each
 $F_k$
is a k-dimensional face of P. Then P is regular if for every two flags
$F_k$
is a k-dimensional face of P. Then P is regular if for every two flags
 $F_0\subset F_1\subset \dots \subset F_{d-1}$
and
$F_0\subset F_1\subset \dots \subset F_{d-1}$
and
 $F^{\prime }_0\subset F^{\prime }_1\subset \dots \subset F^{\prime }_{d-1}$
, there is an isometry of P that maps one flag onto the other.
$F^{\prime }_0\subset F^{\prime }_1\subset \dots \subset F^{\prime }_{d-1}$
, there is an isometry of P that maps one flag onto the other. -
(T2) A polytope is right-angled, or orthogonal, if all dihedral angles are exactly
 $\pi /2$
.
$\pi /2$
.
Before passing to the explanation of the existence of the tiling, let us mention two more properties that follow from (T1) and (T2) (two further properties will be proved in Lemma 3.2 and Lemma 3.3 below).
-
(T3) Every polytope
 $P_n$
has an inscribed circle, whose center we denote by
$P_n$
has an inscribed circle, whose center we denote by
 $p_n$
and whose radius is by definition the in-radius of
$p_n$
and whose radius is by definition the in-radius of
 $P_n$
.
$P_n$
.Indeed, every regular polytope P admits a center, whose existence can be shown as follows. If F is a maximal face of P, then
 $x\mapsto \operatorname {dist}(x,F)$
is a convex function (as follows easily from Proposition 2.2 in [Reference Bridson and Haefliger14, p. 176]). Thus, letting
$x\mapsto \operatorname {dist}(x,F)$
is a convex function (as follows easily from Proposition 2.2 in [Reference Bridson and Haefliger14, p. 176]). Thus, letting
 $\{F_1,\dots ,F_k\}$
be the maximal faces of P, the map
$\{F_1,\dots ,F_k\}$
be the maximal faces of P, the map
 $x\mapsto \operatorname {dist}(x,F_1)^2 +\dots + \operatorname {dist}(x,F_k)^2$
is strictly convex and hence has a unique minimum p. Since the above map is defined only by metric properties, every isometry of P must fix p. Finally, by regularity, p has the same distance to all maximal faces. For further details, we refer to [Reference Bridson and Haefliger14, pp. 178–179].
$x\mapsto \operatorname {dist}(x,F_1)^2 +\dots + \operatorname {dist}(x,F_k)^2$
is strictly convex and hence has a unique minimum p. Since the above map is defined only by metric properties, every isometry of P must fix p. Finally, by regularity, p has the same distance to all maximal faces. For further details, we refer to [Reference Bridson and Haefliger14, pp. 178–179]. -
(T4) There is a number
 $N(d)$
such that every
$N(d)$
such that every
 $P_n$
intersects at most
$P_n$
intersects at most
 $N(d)$
polytopes from the tiling.
$N(d)$
polytopes from the tiling.
Figure 1: The first seventeen isometric octagons tiling the hyperbolic plane.
Indeed, at each vertex of
 $P_n$
, there are exactly
$P_n$
, there are exactly
 $2^d$
polytopes intersecting
$2^d$
polytopes intersecting
 $P_n$
, by the right-angle property. So a (rough) upper bound for
$P_n$
, by the right-angle property. So a (rough) upper bound for
 $N(d)$
is
$N(d)$
is
 $2^d$
times the number of vertices of
$2^d$
times the number of vertices of
 $P_n$
(such a number of vertices is independent of n, as the polytopes are mutually isometric).
$P_n$
(such a number of vertices is independent of n, as the polytopes are mutually isometric).
We now pass to explaining the existence of regular orthogonal tilings
![]() $(P_n)_{n\in \mathbb {N}}$
for
$(P_n)_{n\in \mathbb {N}}$
for
![]() $d=2,3,4$
. By Proposition 6.3.2 and 6.3.9 in [Reference Davis22], every polytope P whose dihedral angles are of the form
$d=2,3,4$
. By Proposition 6.3.2 and 6.3.9 in [Reference Davis22], every polytope P whose dihedral angles are of the form
![]() $\pi /m$
for some integer
$\pi /m$
for some integer
![]() $m\geqslant 2$
(these polytopes are sometimes called Coxeter polytopes) is simple. Hence, by Theorem 6.4.3 in [Reference Davis22], P is a strict fundamental domain of the reflection group generated by reflections across the faces of P. In other words, P intersects every orbit in exactly one point. This implies in particular that the images of P by the elements of the reflection group tessellate
$m\geqslant 2$
(these polytopes are sometimes called Coxeter polytopes) is simple. Hence, by Theorem 6.4.3 in [Reference Davis22], P is a strict fundamental domain of the reflection group generated by reflections across the faces of P. In other words, P intersects every orbit in exactly one point. This implies in particular that the images of P by the elements of the reflection group tessellate
![]() ${\mathbb {H}}^d$
. Thus, every element of the reflection group maps the faces of a polytope
${\mathbb {H}}^d$
. Thus, every element of the reflection group maps the faces of a polytope
![]() $P_n$
to the faces of some other polytope of the tiling.
$P_n$
to the faces of some other polytope of the tiling.
If we restrict our attention to right-angled polytopes, by the above observations, the existence of a right-angled polytope P directly implies that there is a tessellation of
![]() ${\mathbb {H}}^d$
by isometric copies of P. Several explicit constructions of such polytopes for dimensions
${\mathbb {H}}^d$
by isometric copies of P. Several explicit constructions of such polytopes for dimensions
![]() $d=2,3,4$
are available in the literature, and we mention a few of them in the next paragraph. On the other hand, E. B. Vinberg proved in [Reference Vinberg44] that there is no right-angled polytope in
$d=2,3,4$
are available in the literature, and we mention a few of them in the next paragraph. On the other hand, E. B. Vinberg proved in [Reference Vinberg44] that there is no right-angled polytope in
![]() ${\mathbb {H}}^d$
when
${\mathbb {H}}^d$
when
![]() $d\geqslant 5$
; a short proof of this fact can also be found in [Reference Potyagailo and Vinberg42, Section 2]. Consequently, an orthogonal tiling of
$d\geqslant 5$
; a short proof of this fact can also be found in [Reference Potyagailo and Vinberg42, Section 2]. Consequently, an orthogonal tiling of
![]() ${\mathbb {H}}^d$
exists precisely for dimensions
${\mathbb {H}}^d$
exists precisely for dimensions
![]() $d=2,3,4$
.
$d=2,3,4$
.
As it turns out, in dimension
![]() $d=2,3,4$
, an orthogonal tiling can be constructed that is additionally regular. In dimension
$d=2,3,4$
, an orthogonal tiling can be constructed that is additionally regular. In dimension
![]() $d=2$
, there are infinitely many regular orthogonal tilings, one for each integer
$d=2$
, there are infinitely many regular orthogonal tilings, one for each integer
![]() $p\geqslant 5$
. They are obtained by taking a regular right-angled p-gon in
$p\geqslant 5$
. They are obtained by taking a regular right-angled p-gon in
![]() ${\mathbb {H}}^2$
and gluing together
${\mathbb {H}}^2$
and gluing together
![]() $4$
of them at each vertex; by means of the so-called Schläfli symbol, such a configuration is denoted by
$4$
of them at each vertex; by means of the so-called Schläfli symbol, such a configuration is denoted by
![]() $\{p,4\}$
. For instance,
$\{p,4\}$
. For instance,
![]() $\{8, 4\}$
is a tiling via four regular octagons meeting at each vertex, illustrated in Figure 1. In dimension
$\{8, 4\}$
is a tiling via four regular octagons meeting at each vertex, illustrated in Figure 1. In dimension
![]() $d=3$
, a tiling exists described by
$d=3$
, a tiling exists described by
![]() $\{5,3,4\}$
, which is to be read as follows: start with a regular right-angled pentagon in
$\{5,3,4\}$
, which is to be read as follows: start with a regular right-angled pentagon in
![]() ${\mathbb {H}}^2$
and glue three of them at each vertex. This gives a (hyperbolic) dodecahedron
${\mathbb {H}}^2$
and glue three of them at each vertex. This gives a (hyperbolic) dodecahedron
![]() $\{5,3\}$
and gluing
$\{5,3\}$
and gluing
![]() $4$
on each edge gives the tiling. In dimension
$4$
on each edge gives the tiling. In dimension
![]() $d=4$
, instead, one glues together
$d=4$
, instead, one glues together
![]() $3$
dodecahedra on each edge to obtain a
$3$
dodecahedra on each edge to obtain a
![]() $4$
-dimensional polytope
$4$
-dimensional polytope
![]() $\{5,3,3\}$
whose maximal faces are the dodecahedra
$\{5,3,3\}$
whose maximal faces are the dodecahedra
![]() $\{5,3\}$
. Then, gluing
$\{5,3\}$
. Then, gluing
![]() $4$
such polytopes at each
$4$
such polytopes at each
![]() $2$
-dimensional face, one gets the tiling
$2$
-dimensional face, one gets the tiling
![]() $\{5,3,3,4\}$
. A list of all regular tilings of
$\{5,3,3,4\}$
. A list of all regular tilings of
![]() ${\mathbb {H}}^d$
can be found in [Reference Vinberg and Shvartsman45, Section 5.3.3] or [Reference Coxeter19, Sections 2–4] (the orthogonal ones among them are exactly those with
${\mathbb {H}}^d$
can be found in [Reference Vinberg and Shvartsman45, Section 5.3.3] or [Reference Coxeter19, Sections 2–4] (the orthogonal ones among them are exactly those with
![]() $4$
as the last number in their Schläfli symbol).
$4$
as the last number in their Schläfli symbol).
One notable feature of orthogonal tilings, which we will use in the next lemma as well as Section 5, is the following:
Lemma 3.2 Whenever two hyperplanes
![]() $H_1, H_2\subset {\mathbb {H}}^d$
meet orthogonally, the reflections
$H_1, H_2\subset {\mathbb {H}}^d$
meet orthogonally, the reflections
![]() $R_{H_1}$
and
$R_{H_1}$
and
![]() $R_{H_2}$
across them commute and
$R_{H_2}$
across them commute and
![]() $R_{H_1} R_{H_2}= R_{H_2} R_{H_1}= R_{H_1\cap H_2}$
. Further,
$R_{H_1} R_{H_2}= R_{H_2} R_{H_1}= R_{H_1\cap H_2}$
. Further,
![]() $R_{H_2}[H_1] =H_1$
and
$R_{H_2}[H_1] =H_1$
and
![]() $R_{H_2}$
preserves the two half-spaces defined by
$R_{H_2}$
preserves the two half-spaces defined by
![]() $H_1$
.
$H_1$
.
Proof We will prove this statement using the hyperboloid model of
![]() ${\mathbb {H}}^d$
. Since for every point in
${\mathbb {H}}^d$
. Since for every point in
![]() ${\mathbb {H}}^d$
, there exists an automorphism mapping it to the origin, we can assume that
${\mathbb {H}}^d$
, there exists an automorphism mapping it to the origin, we can assume that
![]() $0\in H_1\cap H_2$
. Moreover, up to a rotation around
$0\in H_1\cap H_2$
. Moreover, up to a rotation around
![]() $0$
of
$0$
of
![]() ${\mathbb {H}}^d$
(i.e., a rotation of
${\mathbb {H}}^d$
(i.e., a rotation of
![]() $\mathbb {R}^{d+1}$
around the
$\mathbb {R}^{d+1}$
around the
![]() $x_{d+1}$
axis), we may assume that
$x_{d+1}$
axis), we may assume that
![]() $H_1=\{y\in {\mathbb {H}}^d\colon y_1=0\}$
and
$H_1=\{y\in {\mathbb {H}}^d\colon y_1=0\}$
and
![]() $H_2=\{y\in {\mathbb {H}}^d\colon y_2=0\}$
(recall that angles at the origin
$H_2=\{y\in {\mathbb {H}}^d\colon y_2=0\}$
(recall that angles at the origin
![]() $0_{{\mathbb {H}}^d}$
are Euclidean angles).
$0_{{\mathbb {H}}^d}$
are Euclidean angles).
Then it follows that
![]() $R_{H_1}(x) = (-x_1,x_2,\dots ,x_{d+1})$
and
$R_{H_1}(x) = (-x_1,x_2,\dots ,x_{d+1})$
and
![]() $R_{H_2}(x)=(x_1,-x_2,\dots ,x_{d+1})$
for
$R_{H_2}(x)=(x_1,-x_2,\dots ,x_{d+1})$
for
![]() $x\in {\mathbb {H}}^d$
. Clearly, these two mappings commute, and their composition is the mapping
$x\in {\mathbb {H}}^d$
. Clearly, these two mappings commute, and their composition is the mapping
![]() $x\mapsto (-x_1,-x_2,x_3,\dots ,x_{d+1})$
, which is the reflection across
$x\mapsto (-x_1,-x_2,x_3,\dots ,x_{d+1})$
, which is the reflection across
![]() $H_1\cap H_2$
. The last clause also follows directly from these formulas.
$H_1\cap H_2$
. The last clause also follows directly from these formulas.
As one can already glean from Figure 1, the edges of the octagons combine into geodesic lines, and this is true in general for any regular orthogonal tiling.
Lemma 3.3 Let
![]() $\mathcal {P}=(P_n)_{n\in \mathbb {N}}$
be a regular orthogonal tiling of
$\mathcal {P}=(P_n)_{n\in \mathbb {N}}$
be a regular orthogonal tiling of
![]() ${\mathbb {H}}^d$
,
${\mathbb {H}}^d$
,
![]() $d\leqslant 4$
. Then, there exists a sequence
$d\leqslant 4$
. Then, there exists a sequence
![]() $(H_k)_{k\in \mathbb {N}}$
of hyperplanes in
$(H_k)_{k\in \mathbb {N}}$
of hyperplanes in
![]() ${\mathbb {H}}^d$
such that
${\mathbb {H}}^d$
such that
These
![]() $H_k$
are exactly all the supporting hyperplanes for any maximal face of any
$H_k$
are exactly all the supporting hyperplanes for any maximal face of any
![]() $P_n$
. As a consequence, if R is a reflection across some maximal face,
$P_n$
. As a consequence, if R is a reflection across some maximal face,
 $$\begin{align*}R\left[ \bigcup_{k\in\mathbb{N}}H_k \right]= \bigcup_{k\in\mathbb{N}}H_k. \end{align*}$$
$$\begin{align*}R\left[ \bigcup_{k\in\mathbb{N}}H_k \right]= \bigcup_{k\in\mathbb{N}}H_k. \end{align*}$$
Proof Let
![]() $(H_k)_{k\in \mathbb {N}}$
be the sequence listing all the supporting hyperplanes for any maximal face of any polytope
$(H_k)_{k\in \mathbb {N}}$
be the sequence listing all the supporting hyperplanes for any maximal face of any polytope
![]() $P_n$
. Then the validity of the ‘
$P_n$
. Then the validity of the ‘
![]() $\subset $
’ inclusion is clear.
$\subset $
’ inclusion is clear.
For the converse inclusion, take a hyperplane
![]() $H\in \{H_k\}_{k\in \mathbb {N}}$
. By definition, there is a polytope
$H\in \{H_k\}_{k\in \mathbb {N}}$
. By definition, there is a polytope
![]() $P\in \mathcal {P}$
such that
$P\in \mathcal {P}$
such that ![]() is a maximal face of P. Then M is a regular right-angled polytope in H (which is isometric to
is a maximal face of P. Then M is a regular right-angled polytope in H (which is isometric to
![]() ${\mathbb {H}}^{d-1}$
); hence, the reflection group generated by reflections across the maximal faces of M induces a tiling of H, by copies of M. However, a reflection across a maximal face of M is the restriction to H of a reflection across a hyperplane
${\mathbb {H}}^{d-1}$
); hence, the reflection group generated by reflections across the maximal faces of M induces a tiling of H, by copies of M. However, a reflection across a maximal face of M is the restriction to H of a reflection across a hyperplane
![]() $\tilde {H}$
in
$\tilde {H}$
in
![]() ${\mathbb {H}}^d$
, orthogonal to H (in fact, the reflection across
${\mathbb {H}}^d$
, orthogonal to H (in fact, the reflection across
![]() $\tilde {H}$
maps H to H, by Lemma 3.2). Moreover,
$\tilde {H}$
maps H to H, by Lemma 3.2). Moreover,
![]() $\tilde {H}$
supports a maximal face of P, as P is right-angled. Therefore, the images of M under the reflection group of M are images of maximal faces of P under the reflection group of P. Hence,
$\tilde {H}$
supports a maximal face of P, as P is right-angled. Therefore, the images of M under the reflection group of M are images of maximal faces of P under the reflection group of P. Hence,
![]() $H\subset \bigcup _{n\in \mathbb {N}}\partial P_n$
, as desired.
$H\subset \bigcup _{n\in \mathbb {N}}\partial P_n$
, as desired.
Finally, the last claim follows because R preserves the set
![]() $\bigcup _{n\in \mathbb {N}}\partial P_n$
of faces.
$\bigcup _{n\in \mathbb {N}}\partial P_n$
of faces.
4 Lipschitz functions on polytopes
This section is dedicated to the local part of our construction, where we study the Banach space of Lipschitz functions on a single polytope. The result we prove in this section asserts that the space of all Lipschitz functions that vanish on certain subsets of the boundary of a polytope P is weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
isomorphic to
$^*$
isomorphic to
![]() $\mathrm {Lip}_0(P)$
. Since
$\mathrm {Lip}_0(P)$
. Since
![]() ${\mathbb {H}}^d$
is locally bi-Lipschitz equivalent to
${\mathbb {H}}^d$
is locally bi-Lipschitz equivalent to
![]() $\mathbb {R}^d$
by Lemma 2.1, it is irrelevant if we consider Euclidean or hyperbolic polytopes; therefore, in all the section, we consider polytopes in
$\mathbb {R}^d$
by Lemma 2.1, it is irrelevant if we consider Euclidean or hyperbolic polytopes; therefore, in all the section, we consider polytopes in
![]() $\mathbb {R}^d$
. As we explained in the Introduction, our focus being on the hyperbolic case, we treat the Euclidean case as a black-box; this explains why in this section we will use nonexplicit arguments and we do not have an explicit formula for the isomorphism.
$\mathbb {R}^d$
. As we explained in the Introduction, our focus being on the hyperbolic case, we treat the Euclidean case as a black-box; this explains why in this section we will use nonexplicit arguments and we do not have an explicit formula for the isomorphism.
We begin by introducing the following notation.
Definition 4.1 If S is a subset of a pointed metric space M, we denote by
the space of all Lipschitz functions on M vanishing on S (in addition to vanishing on
![]() $0_M$
).
$0_M$
).
It is easy to see that
![]() $\mathrm {Lip}_{0,S}(M)$
is pointwise closed, and hence weak
$\mathrm {Lip}_{0,S}(M)$
is pointwise closed, and hence weak
![]() $^*$
closed as well. Thus,
$^*$
closed as well. Thus,
![]() $\mathrm {Lip}_{0,S}(M)$
is the dual of a quotient of
$\mathrm {Lip}_{0,S}(M)$
is the dual of a quotient of
![]() $\mathcal {F}(M)$
, and the corresponding weak
$\mathcal {F}(M)$
, and the corresponding weak
![]() $^*$
topology is the restriction of the weak
$^*$
topology is the restriction of the weak
![]() $^*$
topology of
$^*$
topology of
![]() $\mathrm {Lip}_0(M)$
; hence, on bounded sets, it coincides with the pointwise one.
$\mathrm {Lip}_0(M)$
; hence, on bounded sets, it coincides with the pointwise one.
Before the main result of the section, we collect in the following lemma a basic construction of a linear extension operator.
Lemma 4.2 Let
![]() $(M,d)$
be a pointed metric space and
$(M,d)$
be a pointed metric space and
![]() $N\subset M$
be a bounded Lipschitz retract of M with
$N\subset M$
be a bounded Lipschitz retract of M with
![]() $0_M\in N$
. Then for every
$0_M\in N$
. Then for every
![]() $\varepsilon>0$
, there is a bounded, weak
$\varepsilon>0$
, there is a bounded, weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous, linear extension operator
$^*$
continuous, linear extension operator
such that, for every
![]() $f\in \mathrm {Lip}_0(N)$
, the support of
$f\in \mathrm {Lip}_0(N)$
, the support of
![]() $E_{N,\varepsilon }f$
is contained in the set
$E_{N,\varepsilon }f$
is contained in the set
![]() $\overline {B}(N,\varepsilon )=\{x\in M\colon \mathrm {dist}(x,N)\leqslant \varepsilon \}$
.
$\overline {B}(N,\varepsilon )=\{x\in M\colon \mathrm {dist}(x,N)\leqslant \varepsilon \}$
.
Proof Fix a Lipschitz retraction r of M onto N and define the mapping
![]() $\lambda \colon M\to [0,1]$
by
$\lambda \colon M\to [0,1]$
by
![]() $\lambda (x) = \max \{1-\frac { \mathrm {dist}(x,N)}{\varepsilon }, 0\}$
.
$\lambda (x) = \max \{1-\frac { \mathrm {dist}(x,N)}{\varepsilon }, 0\}$
.
![]() $\lambda $
is clearly
$\lambda $
is clearly
![]() $1/\varepsilon $
-Lipschitz and vanishes outside
$1/\varepsilon $
-Lipschitz and vanishes outside
![]() $\overline {B}(N,\varepsilon )$
. Then the mapping
$\overline {B}(N,\varepsilon )$
. Then the mapping
is well defined and bounded since
 $$ \begin{align*} \mathrm{Lip}\left( (f\circ r)\lambda \right) &\leqslant \mathrm{Lip}(f\circ r) \|\lambda\|_\infty + \mathrm{Lip}(\lambda) \|f\circ r\|_\infty\\ &\leqslant \mathrm{Lip}(f)\mathrm{Lip}(r) +\frac{1}{\varepsilon} \|f\|_\infty \leqslant \left(\mathrm{Lip}(r) + \frac{\operatorname{diam} (N)}{\varepsilon}\right) \|f\|_{\mathrm{Lip}_0}. \end{align*} $$
$$ \begin{align*} \mathrm{Lip}\left( (f\circ r)\lambda \right) &\leqslant \mathrm{Lip}(f\circ r) \|\lambda\|_\infty + \mathrm{Lip}(\lambda) \|f\circ r\|_\infty\\ &\leqslant \mathrm{Lip}(f)\mathrm{Lip}(r) +\frac{1}{\varepsilon} \|f\|_\infty \leqslant \left(\mathrm{Lip}(r) + \frac{\operatorname{diam} (N)}{\varepsilon}\right) \|f\|_{\mathrm{Lip}_0}. \end{align*} $$
Finally, the pointwise-to-pointwise continuity of
![]() $E_{N,\varepsilon }$
is clear from the definition.
$E_{N,\varepsilon }$
is clear from the definition.
Proposition 4.3 Let P be a polygon in
![]() $\mathbb {R}^d$
with
$\mathbb {R}^d$
with
![]() $0\in \mathrm {int}(P)$
and let
$0\in \mathrm {int}(P)$
and let
![]() $S\subset \partial P$
be the union of one or more faces (of any dimension) of P. Then,
$S\subset \partial P$
be the union of one or more faces (of any dimension) of P. Then,
Moreover, the isomorphism is weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous.
$^*$
continuous.
Proof Let us first prove that
![]() $\mathrm {Lip}_0(P)$
is weak
$\mathrm {Lip}_0(P)$
is weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
isomorphic to a weak
$^*$
isomorphic to a weak
![]() $^*$
-complemented subspace of
$^*$
-complemented subspace of
![]() $\mathrm {Lip}_{0,S}(P)$
. For this, note that, for
$\mathrm {Lip}_{0,S}(P)$
. For this, note that, for
![]() $\alpha \in (0,1)$
,
$\alpha \in (0,1)$
,
![]() $\mathrm {Lip}_0(P)$
and
$\mathrm {Lip}_0(P)$
and
![]() $\mathrm {Lip}_0(\alpha P)$
are weak
$\mathrm {Lip}_0(\alpha P)$
are weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
isomorphic (P and
$^*$
isomorphic (P and
![]() $\alpha P$
are bi-Lipschitz equivalent). Hence, it is enough to prove that
$\alpha P$
are bi-Lipschitz equivalent). Hence, it is enough to prove that
![]() $\mathrm {Lip}_0(\alpha P)$
is weak
$\mathrm {Lip}_0(\alpha P)$
is weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
isomorphic to a weak
$^*$
isomorphic to a weak
![]() $^*$
-complemented subspace of
$^*$
-complemented subspace of
![]() $\mathrm {Lip}_{0,S}(P)$
. Now,
$\mathrm {Lip}_{0,S}(P)$
. Now,
![]() $\alpha P$
is a Lipschitz retract of P (via the nearest point projection), and it has positive distance to the boundary
$\alpha P$
is a Lipschitz retract of P (via the nearest point projection), and it has positive distance to the boundary
![]() $\partial P$
of P. So, by Lemma 4.2 for
$\partial P$
of P. So, by Lemma 4.2 for
![]() $\varepsilon =\mathrm {dist} (\partial P,\alpha P)/2>0$
, there is a bounded, weak
$\varepsilon =\mathrm {dist} (\partial P,\alpha P)/2>0$
, there is a bounded, weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous, linear extension operator
$^*$
continuous, linear extension operator
such that
![]() $E_{\alpha P,\varepsilon } f(x)=0$
for all
$E_{\alpha P,\varepsilon } f(x)=0$
for all
![]() $x\in \partial P$
(so the image of
$x\in \partial P$
(so the image of
![]() $E_{\alpha P,\varepsilon }$
is contained in
$E_{\alpha P,\varepsilon }$
is contained in
![]() $\mathrm {Lip}_{0,S}(P)$
). As we observed in Section 2, this gives the desired embedding of
$\mathrm {Lip}_{0,S}(P)$
). As we observed in Section 2, this gives the desired embedding of
![]() $\mathrm {Lip}_0(\alpha P)$
into
$\mathrm {Lip}_0(\alpha P)$
into
![]() $\mathrm {Lip}_{0,S}(P)$
.
$\mathrm {Lip}_{0,S}(P)$
.
Next, we show that
![]() $\mathrm {Lip}_{0,S}(P)$
is a weak
$\mathrm {Lip}_{0,S}(P)$
is a weak
![]() $^*$
-complemented subspace of
$^*$
-complemented subspace of
![]() $\mathrm {Lip}_0(P)$
. Consider the subset
$\mathrm {Lip}_0(P)$
. Consider the subset
![]() $S\cup \{0\}$
of P and observe that P is a doubling metric space (as the doubling property passes to subspaces and
$S\cup \{0\}$
of P and observe that P is a doubling metric space (as the doubling property passes to subspaces and
![]() $\mathbb {R}^d$
is doubling). Therefore, we can apply Lee’s and Naor’s extension result [Reference Lee and Naor39] (see Section 2) and find a weak
$\mathbb {R}^d$
is doubling). Therefore, we can apply Lee’s and Naor’s extension result [Reference Lee and Naor39] (see Section 2) and find a weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous linear extension operator
$^*$
continuous linear extension operator
![]() $E\colon \mathrm {Lip}_0(S\cup \{0\})\to \mathrm {Lip}_0(P)$
. Then the map
$E\colon \mathrm {Lip}_0(S\cup \{0\})\to \mathrm {Lip}_0(P)$
. Then the map
is a linear projection onto
![]() $\mathrm {Lip}_{0,S}(P)$
since by definition,
$\mathrm {Lip}_{0,S}(P)$
since by definition,
![]() $Qf$
vanishes on S and for each
$Qf$
vanishes on S and for each
![]() $f\in \mathrm {Lip}_{0,S}(P)$
,
$f\in \mathrm {Lip}_{0,S}(P)$
,
![]() $E(f|_{S\cup \{0\}})=0$
. Hence,
$E(f|_{S\cup \{0\}})=0$
. Hence,
![]() $\mathrm {Lip}_{0,S}(P)$
is a complemented subspace of
$\mathrm {Lip}_{0,S}(P)$
is a complemented subspace of
![]() $\mathrm {Lip}_0(P)$
. In addition, Q is weak
$\mathrm {Lip}_0(P)$
. In addition, Q is weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous since E is.
$^*$
continuous since E is.
Finally, by standard duality, the assertions proved in the previous paragraphs yield that
![]() $\mathrm {Lip}_{0,S}(P)$
is the dual to a complemented subspace Z of
$\mathrm {Lip}_{0,S}(P)$
is the dual to a complemented subspace Z of
![]() $\mathcal {F}(P)$
and
$\mathcal {F}(P)$
and
![]() $\mathcal {F}(P)$
is isomorphic to a complemented subspace of Z. Moreover, P has nonempty interior in
$\mathcal {F}(P)$
is isomorphic to a complemented subspace of Z. Moreover, P has nonempty interior in
![]() $\mathbb {R}^d$
; hence, combining [Reference Kaufmann36, Corollary 3.5] and [Reference Kaufmann36, Theorem 3.1], we obtain that
$\mathbb {R}^d$
; hence, combining [Reference Kaufmann36, Corollary 3.5] and [Reference Kaufmann36, Theorem 3.1], we obtain that
![]() $\mathcal {F}(P)$
is isomorphic to its
$\mathcal {F}(P)$
is isomorphic to its
![]() $\ell _1$
-sum. Therefore, Pełczyński decomposition method assures us that
$\ell _1$
-sum. Therefore, Pełczyński decomposition method assures us that
![]() $\mathcal {F}(P)$
is isomorphic to Z and passing to the duals we reach the sought conclusion.
$\mathcal {F}(P)$
is isomorphic to Z and passing to the duals we reach the sought conclusion.
5 Extension operators and proof of the main result
In this section, we construct a number of extension operators which are the central tools for the proof of the main result. We are using a regular orthogonal tiling, and hence, we consider
![]() ${\mathbb {H}}^d$
only for
${\mathbb {H}}^d$
only for
![]() $d=2,3,4$
. Given a regular orthogonal tiling
$d=2,3,4$
. Given a regular orthogonal tiling
![]() $\mathcal P:=(P_n)_{n\in \mathbb {N}}$
by isometric copies of a single polytope, we denote by
$\mathcal P:=(P_n)_{n\in \mathbb {N}}$
by isometric copies of a single polytope, we denote by
![]() $p_n$
the center point of
$p_n$
the center point of
![]() $P_n$
in the sense of (T3) of Section 3.1 and consider the net
$P_n$
in the sense of (T3) of Section 3.1 and consider the net
![]() $\mathcal {N}:=\{p_n\colon n\in \mathbb {N}\}$
. For the space
$\mathcal {N}:=\{p_n\colon n\in \mathbb {N}\}$
. For the space
![]() $\mathrm {Lip}_0(P_n)$
, we use
$\mathrm {Lip}_0(P_n)$
, we use
![]() $p_n$
as the distinguished point, and for the sake of simplicity, we assume that
$p_n$
as the distinguished point, and for the sake of simplicity, we assume that
![]() $p_1=0$
.
$p_1=0$
.
Using these data, we use the following strategy to prove the main result: In Section 5.1, we use an extension operator from the net
![]() $\mathcal {N}$
to decompose Lipschitz functions on
$\mathcal {N}$
to decompose Lipschitz functions on
![]() ${\mathbb {H}}^d$
into Lipschitz functions on
${\mathbb {H}}^d$
into Lipschitz functions on
![]() $\mathcal {N}$
and (bounded) Lipschitz functions vanishing on
$\mathcal {N}$
and (bounded) Lipschitz functions vanishing on
![]() $\mathcal {N}$
. In Section 5.2, we decompose the latter functions into a sequence of Lipschitz functions on the tiles. In Section 5.3, we use extension operators from the tiles to construct the inverse operator of this decomposition operator. Finally, in Section 5.4, we combine these arguments to finish the proof and state some consequences.
$\mathcal {N}$
. In Section 5.2, we decompose the latter functions into a sequence of Lipschitz functions on the tiles. In Section 5.3, we use extension operators from the tiles to construct the inverse operator of this decomposition operator. Finally, in Section 5.4, we combine these arguments to finish the proof and state some consequences.
5.1 Extension from the net
 $\mathcal N$
$\mathcal N$
In this part, we construct a bounded, weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous linear extension operator from the net
$^*$
continuous linear extension operator from the net
![]() $\mathcal {N}$
to
$\mathcal {N}$
to
![]() ${\mathbb {H}}^d$
. In order to achieve this, we will exploit a Lipschitz partition of unity in the spirit of [Reference Albiac, Ansorena, Cúth and Doucha1, Reference Bruè, Di Marino and Stra16, Reference Johnson, Lindenstrauss and Schechtman35]. Notice that said results cannot be applied directly because
${\mathbb {H}}^d$
. In order to achieve this, we will exploit a Lipschitz partition of unity in the spirit of [Reference Albiac, Ansorena, Cúth and Doucha1, Reference Bruè, Di Marino and Stra16, Reference Johnson, Lindenstrauss and Schechtman35]. Notice that said results cannot be applied directly because
![]() ${\mathbb {H}}^d$
is not a doubling metric space. However, the specific shape of the net, inherited from the tiling, allows a very simple construction of the partition of unity.
${\mathbb {H}}^d$
is not a doubling metric space. However, the specific shape of the net, inherited from the tiling, allows a very simple construction of the partition of unity.
Since the polytopes
![]() $P_n$
are mutually isometric, the in-radius
$P_n$
are mutually isometric, the in-radius
![]() $\mathrm {dist}(p_n, \partial P_n)$
of
$\mathrm {dist}(p_n, \partial P_n)$
of
![]() $P_n$
is the same for all n; thus, we can set
$P_n$
is the same for all n; thus, we can set ![]() . Therefore, when
. Therefore, when
![]() $k\neq n$
,
$k\neq n$
,
![]() $\mathrm {dist}(p_k,P_n)\geqslant \delta $
. Define functions
$\mathrm {dist}(p_k,P_n)\geqslant \delta $
. Define functions
![]() $\varrho _n\colon {\mathbb {H}}^d \to \mathbb {R}$
by
$\varrho _n\colon {\mathbb {H}}^d \to \mathbb {R}$
by ![]() . Then
. Then
![]() $\varrho _n(p_k)= \delta _{k,n}$
and
$\varrho _n(p_k)= \delta _{k,n}$
and
![]() $\varrho _n$
is
$\varrho _n$
is
![]() $1/\delta $
-Lipschitz. Moreover, the restriction of
$1/\delta $
-Lipschitz. Moreover, the restriction of
![]() $\varrho _n$
to
$\varrho _n$
to
![]() $P_k$
is nonzero only when
$P_k$
is nonzero only when
![]() $P_k$
intersects
$P_k$
intersects
![]() $P_n$
. Hence, by (T4), the series
$P_n$
. Hence, by (T4), the series
![]() $\sum _{n=1}^\infty \varrho _n$
is locally a sum of at most
$\sum _{n=1}^\infty \varrho _n$
is locally a sum of at most
![]() $N(d)$
terms, and therefore, it defines a bounded Lipschitz function. Additionally, we have
$N(d)$
terms, and therefore, it defines a bounded Lipschitz function. Additionally, we have
![]() $\sum _{n=1}^\infty \varrho _n(x)\geqslant 1$
for all
$\sum _{n=1}^\infty \varrho _n(x)\geqslant 1$
for all
![]() $x\in {\mathbb {H}}^d$
, as
$x\in {\mathbb {H}}^d$
, as
![]() $\varrho _n$
equals
$\varrho _n$
equals
![]() $1$
on
$1$
on
![]() $P_n$
. Consequently, the functions
$P_n$
. Consequently, the functions
are uniformly Lipschitz, with constant, say,
![]() $L_{\mathcal {N}}$
. Clearly,
$L_{\mathcal {N}}$
. Clearly,
![]() $(\varphi _n)_{n=1}^\infty $
is the desired partition of unity and
$(\varphi _n)_{n=1}^\infty $
is the desired partition of unity and
![]() $\varphi _n(p_k)=\delta _{k,n}$
. We can now proceed to the construction of the extension operator from the net
$\varphi _n(p_k)=\delta _{k,n}$
. We can now proceed to the construction of the extension operator from the net
![]() $\mathcal {N}$
.
$\mathcal {N}$
.
Lemma 5.1 The operator
![]() $E_{\mathcal N}$
defined as
$E_{\mathcal N}$
defined as
is a bounded linear extension operator from the net
![]() $\mathcal N$
to
$\mathcal N$
to
![]() ${\mathbb {H}}^d$
which is weak
${\mathbb {H}}^d$
which is weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous.
$^*$
continuous.
Proof The sum defining
![]() $E_{\mathcal N}f$
is locally finite; thus,
$E_{\mathcal N}f$
is locally finite; thus,
![]() $E_{\mathcal N}$
is clearly a well-defined linear extension operator, and
$E_{\mathcal N}$
is clearly a well-defined linear extension operator, and
![]() $E_{\mathcal {N}}f$
is continuous. In order to bound the Lipschitz constant of
$E_{\mathcal {N}}f$
is continuous. In order to bound the Lipschitz constant of
![]() $E_{\mathcal N}f$
, we use Lemma 2.1. Thus, fix
$E_{\mathcal N}f$
, we use Lemma 2.1. Thus, fix
![]() $f\in \mathrm {Lip}_0(\mathcal N)$
and
$f\in \mathrm {Lip}_0(\mathcal N)$
and
![]() $x,y\in P_n$
, for some
$x,y\in P_n$
, for some
![]() $n\in \mathbb {N}$
. Let
$n\in \mathbb {N}$
. Let
![]() $\{n_1,\dots , n_{N(d)}\}$
be the set of indices corresponding to the polytopes
$\{n_1,\dots , n_{N(d)}\}$
be the set of indices corresponding to the polytopes
![]() $P_k$
that intersect
$P_k$
that intersect
![]() $P_n$
. Hence, we have
$P_n$
. Hence, we have
 $$ \begin{align*} |E_{\mathcal{N}}f(x) - E_{\mathcal{N}}f(y)| =& \left|\sum_{j=1}^{N(d)} \big(\varphi_{n_j}(x) - \varphi_{n_j}(y)\big) f(p_{n_j})\right|\\ =& \left|\sum_{j=1}^{N(d)} \big(\varphi_{n_j}(x) - \varphi_{n_j}(y)\big) \big(f(p_{n_j})-f(p_n)\big)\right|\\ \leqslant& \sum_{j=1}^{N(d)} L_{\mathcal{N}}\ \rho(x,y)\ \mathrm{Lip}(f)\ \rho(p_{n_j},p_n)\leqslant C\ \mathrm{Lip}(f)\ \rho(x,y). \end{align*} $$
$$ \begin{align*} |E_{\mathcal{N}}f(x) - E_{\mathcal{N}}f(y)| =& \left|\sum_{j=1}^{N(d)} \big(\varphi_{n_j}(x) - \varphi_{n_j}(y)\big) f(p_{n_j})\right|\\ =& \left|\sum_{j=1}^{N(d)} \big(\varphi_{n_j}(x) - \varphi_{n_j}(y)\big) \big(f(p_{n_j})-f(p_n)\big)\right|\\ \leqslant& \sum_{j=1}^{N(d)} L_{\mathcal{N}}\ \rho(x,y)\ \mathrm{Lip}(f)\ \rho(p_{n_j},p_n)\leqslant C\ \mathrm{Lip}(f)\ \rho(x,y). \end{align*} $$
Here,
![]() $C= 2\operatorname {diam}(P_n)\ L_{\mathcal {N}}\ N(d)$
, and we used the fact that
$C= 2\operatorname {diam}(P_n)\ L_{\mathcal {N}}\ N(d)$
, and we used the fact that
![]() $\rho (p_{n_j},p_n)\leqslant 2\operatorname {diam}(P_n)$
, since
$\rho (p_{n_j},p_n)\leqslant 2\operatorname {diam}(P_n)$
, since
![]() $P_{n_j}\cap P_n\neq \emptyset $
. According to Lemma 2.1, this inequality proves that
$P_{n_j}\cap P_n\neq \emptyset $
. According to Lemma 2.1, this inequality proves that
![]() $\mathrm {Lip}(E_{\mathcal {N}}f)\leqslant C\mathrm {Lip} (f)$
, whence the boundedness of
$\mathrm {Lip}(E_{\mathcal {N}}f)\leqslant C\mathrm {Lip} (f)$
, whence the boundedness of
![]() $E_{\mathcal {N}}$
.
$E_{\mathcal {N}}$
.
Lastly, to prove weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuity, we need only show pointwise-to-pointwise continuity. So assume that
$^*$
continuity, we need only show pointwise-to-pointwise continuity. So assume that
![]() $(f_k)_{k\in \mathbb {N}}$
is a sequence of Lipschitz functions converging pointwise to some function
$(f_k)_{k\in \mathbb {N}}$
is a sequence of Lipschitz functions converging pointwise to some function
![]() $f\in \mathrm {Lip}_0(\mathcal N)$
. Then, using again local finiteness of the sum,
$f\in \mathrm {Lip}_0(\mathcal N)$
. Then, using again local finiteness of the sum,
5.2 Decomposition into functions on tiles
The aim of this section is to decompose a Lipschitz function on
![]() ${\mathbb {H}}^d$
into a sequence of functions defined on the tiles of our tiling. As a first step, we use the results of the previous section to remove the part of the function defined on the net
${\mathbb {H}}^d$
into a sequence of functions defined on the tiles of our tiling. As a first step, we use the results of the previous section to remove the part of the function defined on the net
![]() $\mathcal {N}$
. More precisely, Lemma 5.1 implies that the mapping
$\mathcal {N}$
. More precisely, Lemma 5.1 implies that the mapping
is a weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous isomorphism (with inverse
$^*$
continuous isomorphism (with inverse
![]() $(g,h)\mapsto E_{\mathcal {N}}(g) + h$
).
$(g,h)\mapsto E_{\mathcal {N}}(g) + h$
).
Hence, our goal now is to decompose a function in
![]() $\mathrm {Lip}_{0,\mathcal {N}}({\mathbb {H}}^d)$
into a sequence of functions defined on the tiles. We start with some geometric preliminaries.
$\mathrm {Lip}_{0,\mathcal {N}}({\mathbb {H}}^d)$
into a sequence of functions defined on the tiles. We start with some geometric preliminaries.
Definition 5.2 Let H be a hyperplane in
![]() ${\mathbb {H}}^d$
not containing the origin
${\mathbb {H}}^d$
not containing the origin
![]() $0$
. The two connected components of
$0$
. The two connected components of
![]() ${\mathbb {H}}^d\setminus H$
are called the open half-spaces defined by H. We denote their closures by
${\mathbb {H}}^d\setminus H$
are called the open half-spaces defined by H. We denote their closures by
![]() $H^+$
and
$H^+$
and
![]() $H^-$
, where
$H^-$
, where
![]() $H^+$
is chosen so that
$H^+$
is chosen so that
![]() $0$
is in the interior of
$0$
is in the interior of
![]() $H^+$
.
$H^+$
.
Let us now fix some notation and parameters. Let
![]() $\mathcal P$
be our tiling of
$\mathcal P$
be our tiling of
![]() ${\mathbb {H}}^d$
and
${\mathbb {H}}^d$
and
![]() $(H_m)_{m\in \mathbb {N}}$
be the sequence of hyperplanes supporting the faces of the tiles
$(H_m)_{m\in \mathbb {N}}$
be the sequence of hyperplanes supporting the faces of the tiles
![]() $P_n$
as in Lemma 3.3. Let
$P_n$
as in Lemma 3.3. Let
![]() $\varepsilon>0$
be a fixed number which is smaller than the in-radius of
$\varepsilon>0$
be a fixed number which is smaller than the in-radius of
![]() $P_m$
and smaller than half of the minimal distance of nonadjacent faces of
$P_m$
and smaller than half of the minimal distance of nonadjacent faces of
![]() $P_m$
. For the hyperplane
$P_m$
. For the hyperplane
![]() $H_m$
, we denote by
$H_m$
, we denote by
![]() $R_m\colon {\mathbb {H}}^d\to {\mathbb {H}}^d$
the reflection across
$R_m\colon {\mathbb {H}}^d\to {\mathbb {H}}^d$
the reflection across
![]() $H_m$
.
$H_m$
.
In order to start the construction of the decomposition, for each hyperplane
![]() $H_n$
, we define a cutoff function
$H_n$
, we define a cutoff function
 $$\begin{align*}\psi_n\colon {\mathbb{H}}^d\to [0,1]\colon \qquad x\mapsto \max\left\{1-\frac{ \mathrm{dist}(x,H_n)}{\varepsilon},0\right\}, \end{align*}$$
$$\begin{align*}\psi_n\colon {\mathbb{H}}^d\to [0,1]\colon \qquad x\mapsto \max\left\{1-\frac{ \mathrm{dist}(x,H_n)}{\varepsilon},0\right\}, \end{align*}$$
which clearly satisfies
![]() $\mathrm {Lip}(\psi _n)\leqslant 1/\varepsilon $
,
$\mathrm {Lip}(\psi _n)\leqslant 1/\varepsilon $
,
![]() $\psi _n(x)=1$
if and only if
$\psi _n(x)=1$
if and only if
![]() $x\in H_n$
, and
$x\in H_n$
, and
![]() $\psi _n(x)=0$
if and only if
$\psi _n(x)=0$
if and only if
![]() $\operatorname {dist}(x,H_n)\geqslant \varepsilon $
.
$\operatorname {dist}(x,H_n)\geqslant \varepsilon $
.
We now construct operators on the space
![]() $(\bigoplus _{m\in \mathbb {N}}\mathrm {Lip}_0(P_m))_{\ell _\infty }$
. In order to simplify the notation, we often interpret this sum as the space of all functions g defined on
$(\bigoplus _{m\in \mathbb {N}}\mathrm {Lip}_0(P_m))_{\ell _\infty }$
. In order to simplify the notation, we often interpret this sum as the space of all functions g defined on
![]() $\bigcup _{m\in \mathbb {N}} \mathrm {int}(P_m)\subset {\mathbb {H}}^d$
which are Lipschitz on every
$\bigcup _{m\in \mathbb {N}} \mathrm {int}(P_m)\subset {\mathbb {H}}^d$
which are Lipschitz on every
![]() $\mathrm {int}(P_m)$
with
$\mathrm {int}(P_m)$
with
![]() $\sup _{m\in \mathbb {N}} \mathrm {Lip}(g|_{P_m})< \infty $
and that vanish on the net
$\sup _{m\in \mathbb {N}} \mathrm {Lip}(g|_{P_m})< \infty $
and that vanish on the net
![]() $\mathcal {N}$
. More precisely, to a sequence
$\mathcal {N}$
. More precisely, to a sequence
![]() $(g_m)_{m\in \mathbb {N}}$
, we associate the function g defined to be equal to
$(g_m)_{m\in \mathbb {N}}$
, we associate the function g defined to be equal to
![]() $g_m$
on
$g_m$
on
![]() $\mathrm {int}(P_m)$
, for every
$\mathrm {int}(P_m)$
, for every
![]() $m\in \mathbb {N}$
; vice versa, to a function g, we associate the sequence
$m\in \mathbb {N}$
; vice versa, to a function g, we associate the sequence
![]() $(g_m)_{m\in \mathbb {N}}$
, where
$(g_m)_{m\in \mathbb {N}}$
, where
![]() $g_m$
is the unique continuous extension of
$g_m$
is the unique continuous extension of
![]() $g|_{\mathrm {int} (P_m)}$
to
$g|_{\mathrm {int} (P_m)}$
to
![]() $P_m$
. The important advantage of this interpretation is that we do not consider values on the boundaries of the tiles, which simplifies several formulas. As a first instance of this, this interpretation allows us to identify
$P_m$
. The important advantage of this interpretation is that we do not consider values on the boundaries of the tiles, which simplifies several formulas. As a first instance of this, this interpretation allows us to identify
![]() $\mathrm {Lip}_{0,\mathcal {N}}({\mathbb {H}}^d)$
with the subspace of all functions admitting a continuous extension to
$\mathrm {Lip}_{0,\mathcal {N}}({\mathbb {H}}^d)$
with the subspace of all functions admitting a continuous extension to
![]() ${\mathbb {H}}^d$
.
${\mathbb {H}}^d$
.
With these preparations, we are now able to define the operator
by setting
 $$\begin{align*}(\chi_n g)(x) = \begin{cases} g(x) & \text{for}\;x\in H_n^{-}, \\ g(x) - \psi_n(x) g(R_n(x)) &\text{for}\; x\in H_n^+. \end{cases} \end{align*}$$
$$\begin{align*}(\chi_n g)(x) = \begin{cases} g(x) & \text{for}\;x\in H_n^{-}, \\ g(x) - \psi_n(x) g(R_n(x)) &\text{for}\; x\in H_n^+. \end{cases} \end{align*}$$
Notice that in the definition of
![]() $\chi _n$
, we used the interpretation explained above. Also, according to Lemma 3.3,
$\chi _n$
, we used the interpretation explained above. Also, according to Lemma 3.3,
![]() $R_n$
maps
$R_n$
maps
![]() $\bigcup _{m\in \mathbb {N}} \mathrm {int}(P_m)$
to itself; thus, we can legitimately evaluate g at the point
$\bigcup _{m\in \mathbb {N}} \mathrm {int}(P_m)$
to itself; thus, we can legitimately evaluate g at the point
![]() $R_n(x)$
.
$R_n(x)$
.
Since reflections are isometries and g is bounded, the operator
![]() $\chi _n$
is bounded and it is clearly also weak
$\chi _n$
is bounded and it is clearly also weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous. Also note that since
$^*$
continuous. Also note that since
![]() $\chi _n$
does not change, the values of g on
$\chi _n$
does not change, the values of g on
![]() $H_n^-$
and
$H_n^-$
and
![]() $R_n(x)\in H_n^-$
whenever
$R_n(x)\in H_n^-$
whenever
![]() $x\in H_n^+$
, its inverse is the operator defined by
$x\in H_n^+$
, its inverse is the operator defined by
 $$\begin{align*}(\chi_n^{-1} g)(x) = \begin{cases} g(x) & \text{for}\;x\in H_n^{-}, \\ g(x) + \psi_n(x) g(R_n(x)) &\text{for}\; x\in H_n^+. \end{cases} \end{align*}$$
$$\begin{align*}(\chi_n^{-1} g)(x) = \begin{cases} g(x) & \text{for}\;x\in H_n^{-}, \\ g(x) + \psi_n(x) g(R_n(x)) &\text{for}\; x\in H_n^+. \end{cases} \end{align*}$$
We denote by
![]() $\chi _{1,\ldots ,n}:=\chi _n\circ \cdots \circ \chi _1$
the composition of
$\chi _{1,\ldots ,n}:=\chi _n\circ \cdots \circ \chi _1$
the composition of
![]() $\chi _1,\ldots , \chi _n$
and note that it satisfies
$\chi _1,\ldots , \chi _n$
and note that it satisfies
![]() $\chi _{1,\ldots ,n}^{-1} = \chi _1^{-1}\circ \cdots \circ \chi _n^{-1}$
.
$\chi _{1,\ldots ,n}^{-1} = \chi _1^{-1}\circ \cdots \circ \chi _n^{-1}$
.
Given a function
![]() $g\in \mathrm {Lip}_{0,\mathcal N}({\mathbb {H}}^d)$
, we define a function
$g\in \mathrm {Lip}_{0,\mathcal N}({\mathbb {H}}^d)$
, we define a function
![]() $g_m\colon P_m\to \mathbb {R}$
by
$g_m\colon P_m\to \mathbb {R}$
by
Note that for each m, there is an
![]() $N_m$
such that
$N_m$
such that
![]() $\chi _{1,\ldots ,n}(g)(x)$
does not change for
$\chi _{1,\ldots ,n}(g)(x)$
does not change for
![]() $n\geqslant N_m$
. Hence, the above limit exists since the sequence is eventually constant, and the index where it becomes constant only depends on
$n\geqslant N_m$
. Hence, the above limit exists since the sequence is eventually constant, and the index where it becomes constant only depends on
![]() $P_m$
and not on the individual point
$P_m$
and not on the individual point
![]() $x\in P_m$
.
$x\in P_m$
.
Let us now consider the linear mapping
which will eventually be the main ingredient for our isomorphism. Since it is not surjective between the above spaces, we have to determine a suitable codomain. With this in mind, for each
![]() $m\in \mathbb {N}$
, we define
$m\in \mathbb {N}$
, we define
 $$ \begin{align} S_m:=\bigcup_{\substack{n\in\mathbb{N}\\P_m\subset H_n^+}}H_n\cap P_m. \end{align} $$
$$ \begin{align} S_m:=\bigcup_{\substack{n\in\mathbb{N}\\P_m\subset H_n^+}}H_n\cap P_m. \end{align} $$
Now we are able to define the desired operator
and start checking that it has the desired properties.
Lemma 5.3 The linear operator
![]() $\Phi $
maps
$\Phi $
maps
![]() $\mathrm {Lip}_{0,\mathcal N}({\mathbb {H}}^d)$
into
$\mathrm {Lip}_{0,\mathcal N}({\mathbb {H}}^d)$
into
![]() $\big (\bigoplus _{m\in \mathbb {N}}\mathrm {Lip}_{0,S_m}(P_m)\big )_{\ell _\infty }$
. Moreover, it is bounded and weak
$\big (\bigoplus _{m\in \mathbb {N}}\mathrm {Lip}_{0,S_m}(P_m)\big )_{\ell _\infty }$
. Moreover, it is bounded and weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous.
$^*$
continuous.
Proof We first check that
![]() $\Phi (g)$
is a sequence of Lipschitz functions whose Lipschitz constants are bounded by a multiple of the Lipschitz constant of g. Since
$\Phi (g)$
is a sequence of Lipschitz functions whose Lipschitz constants are bounded by a multiple of the Lipschitz constant of g. Since
![]() $g\circ R_n$
and
$g\circ R_n$
and
![]() $\psi _n$
are Lipschitz and bounded, the standard product formula gives us that
$\psi _n$
are Lipschitz and bounded, the standard product formula gives us that
![]() $\chi _n$
is bounded with
$\chi _n$
is bounded with
![]() $\|\chi _n\|= \|\chi _1\|$
for all n. Moreover,
$\|\chi _n\|= \|\chi _1\|$
for all n. Moreover,
![]() $\chi _n$
only changes its argument on an
$\chi _n$
only changes its argument on an
![]() $\varepsilon $
-neighborhood of
$\varepsilon $
-neighborhood of
![]() $H_n$
, and
$H_n$
, and
![]() $P_m$
intersects said neighborhood if and only if
$P_m$
intersects said neighborhood if and only if
![]() $H_n$
supports a face of
$H_n$
supports a face of
![]() $P_m$
. Hence, the number of faces
$P_m$
. Hence, the number of faces
![]() $N(d)$
of the polytopes
$N(d)$
of the polytopes
![]() $P_m$
gives us the number of times the function g can at most be changed on that tile during the limit process that produces
$P_m$
gives us the number of times the function g can at most be changed on that tile during the limit process that produces
![]() $\Phi (g)$
. Thus, the Lipschitz constant of
$\Phi (g)$
. Thus, the Lipschitz constant of
![]() $\Phi (g)_m$
is at most
$\Phi (g)_m$
is at most
Also,
![]() $\Phi (g)(p_m)=g(p_m)=0$
because
$\Phi (g)(p_m)=g(p_m)=0$
because
![]() $p_m\in \mathcal N$
and the center-point
$p_m\in \mathcal N$
and the center-point
![]() $p_m$
of any
$p_m$
of any
![]() $P_m$
is not in an
$P_m$
is not in an
![]() $\varepsilon $
-neighborhood of any
$\varepsilon $
-neighborhood of any
![]() $H_n$
. It follows that
$H_n$
. It follows that
![]() $\Phi (g)_m\in \mathrm {Lip}_0(P_m)$
. Note that the above inequality also shows the boundedness of
$\Phi (g)_m\in \mathrm {Lip}_0(P_m)$
. Note that the above inequality also shows the boundedness of
![]() $\Phi $
. By the same reason, the weak
$\Phi $
. By the same reason, the weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuity of
$^*$
continuity of
![]() $\chi _n$
implies that
$\chi _n$
implies that
![]() $\Phi $
is also weak
$\Phi $
is also weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous.
$^*$
continuous.
To conclude, we need to check that
![]() $(\Phi (g))_m$
vanishes on
$(\Phi (g))_m$
vanishes on
![]() $S_m$
. For this aim, assume
$S_m$
. For this aim, assume
![]() $x\in P_m\cap H_n$
and
$x\in P_m\cap H_n$
and
![]() $P_m\subset H_n^+$
and observe that
$P_m\subset H_n^+$
and observe that
 $$\begin{align*}\chi_{1,\ldots,n}(g)(x)= \chi_{1,\ldots,n-1}(g)(x) - \underset{=1}{\underbrace{\psi_n(x)}}(\chi_{1,\ldots,n-1}(g)(x))(\underset{=x}{\underbrace{R_nx}}) = 0. \end{align*}$$
$$\begin{align*}\chi_{1,\ldots,n}(g)(x)= \chi_{1,\ldots,n-1}(g)(x) - \underset{=1}{\underbrace{\psi_n(x)}}(\chi_{1,\ldots,n-1}(g)(x))(\underset{=x}{\underbrace{R_nx}}) = 0. \end{align*}$$
So at the n-th step of our limit process, the values of our function
![]() $\chi _{1,\dots ,n}g$
are set to zero everywhere along
$\chi _{1,\dots ,n}g$
are set to zero everywhere along
![]() $H_n$
on the tiles that lie within
$H_n$
on the tiles that lie within
![]() $H_n^+$
. To express this briefly, we say that
$H_n^+$
. To express this briefly, we say that
![]() $\chi _{1,\dots ,n}g$
vanishes on
$\chi _{1,\dots ,n}g$
vanishes on
![]() $\partial H_n^+$
. We now have to show that this value of zero is retained by all the subsequent functions
$\partial H_n^+$
. We now have to show that this value of zero is retained by all the subsequent functions
![]() $\chi _{1,\dots ,k}g$
,
$\chi _{1,\dots ,k}g$
,
![]() $k>n$
. We will do this by induction.
$k>n$
. We will do this by induction.
So fix
![]() $k>n$
and assume that
$k>n$
and assume that
![]() $\chi _{1,\dots ,k-1}g(x)=0$
for
$\chi _{1,\dots ,k-1}g(x)=0$
for
![]() $x\in \partial H_n^+$
. To show that
$x\in \partial H_n^+$
. To show that
![]() $\chi _{1,\dots ,k}g(x)=0$
as well, we distinguish two cases. If
$\chi _{1,\dots ,k}g(x)=0$
as well, we distinguish two cases. If
![]() $H_k$
and
$H_k$
and
![]() $H_n$
are not orthogonal, it follows from our choice of
$H_n$
are not orthogonal, it follows from our choice of
![]() $\varepsilon $
that
$\varepsilon $
that
![]() $\psi _k$
is zero on
$\psi _k$
is zero on
![]() $H_n$
. Hence,
$H_n$
. Hence,
![]() $\chi _{1,\dots ,k}g(x)=\chi _{1,\dots ,k-1}g(x)=0$
for
$\chi _{1,\dots ,k}g(x)=\chi _{1,\dots ,k-1}g(x)=0$
for
![]() $x\in \partial H_n^+$
. However, if
$x\in \partial H_n^+$
. However, if
![]() $H_k$
is orthogonal to
$H_k$
is orthogonal to
![]() $H_n$
, Lemma 3.2 implies that
$H_n$
, Lemma 3.2 implies that
![]() $R_k[H_n]=H_n$
and
$R_k[H_n]=H_n$
and
![]() $R_k[H_n^+]= H_n^+$
. Therefore,
$R_k[H_n^+]= H_n^+$
. Therefore,
![]() $\chi _{1,\dots ,k-1}g(R_k x)=0$
when
$\chi _{1,\dots ,k-1}g(R_k x)=0$
when
![]() $x\in \partial H_n^+$
. As before, it follows that
$x\in \partial H_n^+$
. As before, it follows that
![]() $\chi _{1,\dots ,k}g$
vanishes on
$\chi _{1,\dots ,k}g$
vanishes on
![]() $\partial H_n^+$
, which finishes the proof.
$\partial H_n^+$
, which finishes the proof.
In the following subsection, we will construct an inverse operator for
![]() $\Phi $
, thus showing that
$\Phi $
, thus showing that
![]() $\Phi $
is an isomorphism.
$\Phi $
is an isomorphism.
5.3 Extension operators from the tiles and inverse of
 $\Phi $
$\Phi $
The goal of this section is to construct a linear extension operator from
![]() $\mathrm {Lip}_{0,S_m}(P_m)$
to
$\mathrm {Lip}_{0,S_m}(P_m)$
to
![]() $\mathrm {Lip}_{0,\mathcal {N}}({\mathbb {H}}^d)$
which works well with the decomposition considered in the previous section and allows us to show that the operator
$\mathrm {Lip}_{0,\mathcal {N}}({\mathbb {H}}^d)$
which works well with the decomposition considered in the previous section and allows us to show that the operator
![]() $\Phi $
is an isomorphism. The interpretation of
$\Phi $
is an isomorphism. The interpretation of
![]() $(\bigoplus _{k\in \mathbb {N}}\mathrm {Lip}_{0}(P_k))_{\ell _\infty }$
and its subspace
$(\bigoplus _{k\in \mathbb {N}}\mathrm {Lip}_{0}(P_k))_{\ell _\infty }$
and its subspace
![]() $(\bigoplus _{k\in \mathbb {N}}\mathrm {Lip}_{0,S_k}(P_k))_{\ell _\infty }$
considered in the previous section allows us to view the space
$(\bigoplus _{k\in \mathbb {N}}\mathrm {Lip}_{0,S_k}(P_k))_{\ell _\infty }$
considered in the previous section allows us to view the space
![]() $\mathrm {Lip}_{0,S_m}(P_m)$
as a subset of
$\mathrm {Lip}_{0,S_m}(P_m)$
as a subset of
![]() $(\bigoplus _{k\in \mathbb {N}}\mathrm {Lip}_{0,S_k}(P_k))_{\ell _\infty }$
, by setting the function equal to zero outside of
$(\bigoplus _{k\in \mathbb {N}}\mathrm {Lip}_{0,S_k}(P_k))_{\ell _\infty }$
, by setting the function equal to zero outside of
![]() $P_m$
.
$P_m$
.
For the construction of the extension operator for
![]() $\mathrm {Lip}_{0,S_m}(P_m)$
, let
$\mathrm {Lip}_{0,S_m}(P_m)$
, let
![]() $n_1>\dotsb >n_s$
be the natural numbers such that the hyperplane
$n_1>\dotsb >n_s$
be the natural numbers such that the hyperplane
![]() $H_{n_j}$
supports a face of
$H_{n_j}$
supports a face of
![]() $P_m$
which is not contained in
$P_m$
which is not contained in
![]() $S_m$
. As a first step, we define the operator
$S_m$
. As a first step, we define the operator
 $$\begin{align*}\mathrm{Lip}_{0,S_m}(P_m)\to\left(\bigoplus_{m\in\mathbb{N}}\mathrm{Lip}_{0}(P_m)\right)_{\ell_\infty}\colon \qquad h \mapsto(\chi_{n_s}^{-1}\circ \dots\circ \chi_{n_1}^{-1})(h). \end{align*}$$
$$\begin{align*}\mathrm{Lip}_{0,S_m}(P_m)\to\left(\bigoplus_{m\in\mathbb{N}}\mathrm{Lip}_{0}(P_m)\right)_{\ell_\infty}\colon \qquad h \mapsto(\chi_{n_s}^{-1}\circ \dots\circ \chi_{n_1}^{-1})(h). \end{align*}$$
The next lemma shows that
![]() $(\chi _{n_s}^{-1}\circ \dots \circ \chi _{n_1}^{-1})(h)$
admits a continuous extension to
$(\chi _{n_s}^{-1}\circ \dots \circ \chi _{n_1}^{-1})(h)$
admits a continuous extension to
![]() ${\mathbb {H}}^d$
, and hence, we may define the extension operator
${\mathbb {H}}^d$
, and hence, we may define the extension operator
where
![]() $E_mh$
is the unique continuous extension of
$E_mh$
is the unique continuous extension of
![]() $(\chi _{n_s}^{-1}\circ \dots \circ \chi _{n_1}^{-1})(h)$
to
$(\chi _{n_s}^{-1}\circ \dots \circ \chi _{n_1}^{-1})(h)$
to
![]() ${\mathbb {H}}^d$
.
${\mathbb {H}}^d$
.
Lemma 5.4 The operator
![]() $E_m$
is well defined, bounded, linear, and weak
$E_m$
is well defined, bounded, linear, and weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous. Moreover,
$^*$
continuous. Moreover,
![]() $\|E_m\|$
is bounded by a constant depending only on
$\|E_m\|$
is bounded by a constant depending only on
![]() $\varepsilon $
, the number of faces of
$\varepsilon $
, the number of faces of
![]() $P_m$
and the diameter of
$P_m$
and the diameter of
![]() $P_m$
.
$P_m$
.
Proof In order to show that
![]() $E_m$
is well defined, we have to show that
$E_m$
is well defined, we have to show that
![]() $g:=(\chi _{n_s}^{-1}\dots \chi _{n_1}^{-1})(h)$
admits a continuous extension to
$g:=(\chi _{n_s}^{-1}\dots \chi _{n_1}^{-1})(h)$
admits a continuous extension to
![]() ${\mathbb {H}}^d$
. We show this in an inductive manner. Note that no hyperplane
${\mathbb {H}}^d$
. We show this in an inductive manner. Note that no hyperplane
![]() $H_n$
intersects the interior of
$H_n$
intersects the interior of
![]() $P_m$
and, by definition of
$P_m$
and, by definition of
![]() $S_m$
(see (5.1)),
$S_m$
(see (5.1)),
![]() $H_{n_j}^{+}$
is the half-space separated from
$H_{n_j}^{+}$
is the half-space separated from
![]() $P_m$
by
$P_m$
by
![]() $H_{n_j}$
(otherwise,
$H_{n_j}$
(otherwise,
![]() $H_{n_j}$
would support a face contained in
$H_{n_j}$
would support a face contained in
![]() $S_m$
, which it does not by definition of
$S_m$
, which it does not by definition of
![]() $n_1,\dots ,n_s$
).
$n_1,\dots ,n_s$
).
Since we think of
![]() $C_k:=\bigcup _{j=k+1}^{s} \mathrm {int}(H_{n_j}^{+})$
as the set to where we have not yet extended our function in the k-th step, we now show that
$C_k:=\bigcup _{j=k+1}^{s} \mathrm {int}(H_{n_j}^{+})$
as the set to where we have not yet extended our function in the k-th step, we now show that
![]() $g_k:=(\chi _{n_{k}}^{-1}\circ \dots \circ \chi _{n_{1}}^{-1})(h)$
has an extension to
$g_k:=(\chi _{n_{k}}^{-1}\circ \dots \circ \chi _{n_{1}}^{-1})(h)$
has an extension to
![]() ${\mathbb {H}}^d$
which is zero on
${\mathbb {H}}^d$
which is zero on
![]() $C_k$
and continuous on
$C_k$
and continuous on
![]() ${\mathbb {H}}^d\setminus C_k$
. Since
${\mathbb {H}}^d\setminus C_k$
. Since
![]() $g=g_s$
and
$g=g_s$
and
![]() $C_s=\emptyset $
this will prove our claim.
$C_s=\emptyset $
this will prove our claim.
The function
![]() $g_0=h$
is zero outside of
$g_0=h$
is zero outside of
![]() $P_m$
and hence on
$P_m$
and hence on
![]() $C_0$
and
$C_0$
and
![]() $({\mathbb {H}}^d\setminus C_0)\setminus P_m$
. Since the (relative) boundary of
$({\mathbb {H}}^d\setminus C_0)\setminus P_m$
. Since the (relative) boundary of
![]() $P_m$
in the set
$P_m$
in the set
![]() ${\mathbb {H}}^d\setminus C_0$
is precisely
${\mathbb {H}}^d\setminus C_0$
is precisely
![]() $S_m$
and
$S_m$
and
![]() $h_m$
vanishes there,
$h_m$
vanishes there,
![]() $g_0$
has a continuous extension to
$g_0$
has a continuous extension to
![]() ${\mathbb {H}}^d\setminus C_0$
.
${\mathbb {H}}^d\setminus C_0$
.
Let us assume now that we have already shown that
![]() $g_{k-1}$
has an extension to
$g_{k-1}$
has an extension to
![]() ${\mathbb {H}}^d$
which is zero on
${\mathbb {H}}^d$
which is zero on
![]() $C_{k-1}$
and continuous on
$C_{k-1}$
and continuous on
![]() ${\mathbb {H}}^d\setminus C_{k-1}$
. By abuse of notation, we call this extension
${\mathbb {H}}^d\setminus C_{k-1}$
. By abuse of notation, we call this extension
![]() $g_{k-1}$
as well. We now have to check that
$g_{k-1}$
as well. We now have to check that
![]() $g_{k}$
also has the desired properties.
$g_{k}$
also has the desired properties.
We first check that
![]() $g_k$
vanishes on
$g_k$
vanishes on
![]() $C_k$
and recall that
$C_k$
and recall that
![]() $g_k(x)=g_{k-1}(x)$
for
$g_k(x)=g_{k-1}(x)$
for
![]() $x\in H_{n_k}^{-}$
and
$x\in H_{n_k}^{-}$
and
![]() $g_{k}(x) = g_{k-1}(x) + \psi _n(x) g_{k-1}(R_{n_k}x)$
for
$g_{k}(x) = g_{k-1}(x) + \psi _n(x) g_{k-1}(R_{n_k}x)$
for
![]() $x\in H_{n_k}^+$
. We distinguish between two cases: If for
$x\in H_{n_k}^+$
. We distinguish between two cases: If for
![]() $j>k$
we have
$j>k$
we have
![]() $H_{n_j}\cap H_{n_{k}}\neq \emptyset $
, these hyperplanes are orthogonal, and hence,
$H_{n_j}\cap H_{n_{k}}\neq \emptyset $
, these hyperplanes are orthogonal, and hence,
![]() $x\in H_{n_j}^+$
if and only if
$x\in H_{n_j}^+$
if and only if
![]() $R_{n_{k}}x \in H_{n_j}^+$
, and hence,
$R_{n_{k}}x \in H_{n_j}^+$
, and hence,
![]() $g_k(x)=0$
for
$g_k(x)=0$
for
![]() $x\in \mathrm {int}\,(H_{n_j}^+)$
. For the other case, note that
$x\in \mathrm {int}\,(H_{n_j}^+)$
. For the other case, note that
![]() $H_{n_{k}}$
cannot be in
$H_{n_{k}}$
cannot be in
![]() $H_{n_j}^+$
since otherwise the face of
$H_{n_j}^+$
since otherwise the face of
![]() $P_m$
contained in
$P_m$
contained in
![]() $H_{n_{k}}$
would have to be in
$H_{n_{k}}$
would have to be in
![]() $H_{n_j}^+$
, which is only possible if it was in
$H_{n_j}^+$
, which is only possible if it was in
![]() $H_{n_j}$
, which contradicts
$H_{n_j}$
, which contradicts
![]() $H_{n_{k}}\cap H_{n_j}=\emptyset $
. Hence, we have
$H_{n_{k}}\cap H_{n_j}=\emptyset $
. Hence, we have
![]() $\mathrm {dist}\,(H_{n_j}^+, H_{n_{k}})>2\varepsilon $
, and therefore,
$\mathrm {dist}\,(H_{n_j}^+, H_{n_{k}})>2\varepsilon $
, and therefore,
![]() $g_k(x) = g_{k-1}(x)=0$
for
$g_k(x) = g_{k-1}(x)=0$
for
![]() $x\in H_{n_{s-k+1}}$
.
$x\in H_{n_{s-k+1}}$
.
In order to show that
![]() $g_k$
has a continuous extension to
$g_k$
has a continuous extension to
![]() ${\mathbb {H}}^d\setminus C_k$
, let
${\mathbb {H}}^d\setminus C_k$
, let
![]() $z\in H_{n_k}\setminus C_k$
and note that
$z\in H_{n_k}\setminus C_k$
and note that
![]() $g_{k-1}(x)=0$
for
$g_{k-1}(x)=0$
for
![]() $x\in \mathrm {int}(H_{n_k}^{-})$
. Hence,
$x\in \mathrm {int}(H_{n_k}^{-})$
. Hence,
where x converges to z in the interior of
![]() $H_{n_k}^{-}$
since
$H_{n_k}^{-}$
since
![]() $\psi _{n_k}(z)=1$
and
$\psi _{n_k}(z)=1$
and
![]() $R_{n_k}(z)=z$
. This finishes the proof of the well-definedness of
$R_{n_k}(z)=z$
. This finishes the proof of the well-definedness of
![]() $E_m$
.
$E_m$
.
Linearity and pointwise-to-pointwise continuity are clear. Since
![]() $\chi _{n_s}^{-1}\dots \chi _{n_1}^{-1}$
is the composition of bounded operators on
$\chi _{n_s}^{-1}\dots \chi _{n_1}^{-1}$
is the composition of bounded operators on
![]() $(\bigoplus _{m\in \mathbb {N}}\mathrm {Lip}_{0}(P_m))_{\ell _\infty }$
and
$(\bigoplus _{m\in \mathbb {N}}\mathrm {Lip}_{0}(P_m))_{\ell _\infty }$
and
![]() $E_mh_m$
is continuous, boundedness of
$E_mh_m$
is continuous, boundedness of
![]() $E_m$
follows from Lemma 2.1 and
$E_m$
follows from Lemma 2.1 and
![]() $\|E_m\|\leqslant \|\chi _{n_s}^{-1}\circ \dots \circ \chi _{n_1}^{-1}\|$
. Finally, note that this norm only depends on
$\|E_m\|\leqslant \|\chi _{n_s}^{-1}\circ \dots \circ \chi _{n_1}^{-1}\|$
. Finally, note that this norm only depends on
![]() $\varepsilon $
, s, and the diameter of
$\varepsilon $
, s, and the diameter of
![]() $P_m$
and that s is at most the number of faces of
$P_m$
and that s is at most the number of faces of
![]() $P_m$
.
$P_m$
.
Remark 5.5 Note that applying
![]() $\chi _{n}^{-1}$
for n distinct from
$\chi _{n}^{-1}$
for n distinct from
![]() $n_1,\ldots ,n_s$
in definition of
$n_1,\ldots ,n_s$
in definition of
![]() $E_m$
does not change anything, as the function we are working with is zero on the interior of
$E_m$
does not change anything, as the function we are working with is zero on the interior of
![]() $H_n^{-}$
, so instead of using
$H_n^{-}$
, so instead of using
![]() $\chi _{n_s}^{-1}\circ \cdots \circ \chi _{n_1}^{-1}$
, we can also use
$\chi _{n_s}^{-1}\circ \cdots \circ \chi _{n_1}^{-1}$
, we can also use
![]() $\chi _{1,\ldots ,n_1}^{-1}$
or even
$\chi _{1,\ldots ,n_1}^{-1}$
or even
![]() $\chi _{1,\ldots ,k}^{-1}$
for every
$\chi _{1,\ldots ,k}^{-1}$
for every
![]() $k\geqslant n_1$
.
$k\geqslant n_1$
.
We are now in position to define the operator
(where the sum is meant to be taken pointwise) and show that it is the inverse of
![]() $\Phi $
.
$\Phi $
.
Proposition 5.6
![]() $\Psi $
is well defined, linear, bounded, weak
$\Psi $
is well defined, linear, bounded, weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous, and the inverse of
$^*$
continuous, and the inverse of
![]() $\Phi $
.
$\Phi $
.
Proof The sum in the definition of
![]() $\Psi $
is locally finite with a uniform bound
$\Psi $
is locally finite with a uniform bound
![]() $N(d)$
on the number of summands; thus,
$N(d)$
on the number of summands; thus,
![]() $\Psi $
is a bounded linear operator by Lemma 5.4. Since weak
$\Psi $
is a bounded linear operator by Lemma 5.4. Since weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuity of
$^*$
continuity of
![]() $\Psi $
is easy to see, we are left to show that
$\Psi $
is easy to see, we are left to show that
![]() $\Psi $
is the inverse of
$\Psi $
is the inverse of
![]() $\Phi $
.
$\Phi $
.
We start by showing that
![]() $\Phi \circ \Psi = \mathrm {Id}$
. For this, let
$\Phi \circ \Psi = \mathrm {Id}$
. For this, let
![]() $(h_m)_{m\in \mathbb {N}} \in (\bigoplus _{m\in \mathbb {N}} \mathrm {Lip}_{0,S_m}(P_m))_{\ell _\infty }$
and fix an arbitrary
$(h_m)_{m\in \mathbb {N}} \in (\bigoplus _{m\in \mathbb {N}} \mathrm {Lip}_{0,S_m}(P_m))_{\ell _\infty }$
and fix an arbitrary
![]() $k\in \mathbb {N}$
. It is enough to check that
$k\in \mathbb {N}$
. It is enough to check that
![]() $(\Phi (\Psi ((h_m)_{m\in \mathbb {N}})))_k(x) = h_k(x)$
for x in the interior of
$(\Phi (\Psi ((h_m)_{m\in \mathbb {N}})))_k(x) = h_k(x)$
for x in the interior of
![]() $P_k$
. Recall that in Section 5.2, we observed that there is an index
$P_k$
. Recall that in Section 5.2, we observed that there is an index
![]() $N_k\in \mathbb {N}$
such that
$N_k\in \mathbb {N}$
such that
![]() $(\chi _{1,\ldots ,n}g)(x)=(\chi _{1,\dots ,N_k}g)(x)$
for
$(\chi _{1,\ldots ,n}g)(x)=(\chi _{1,\dots ,N_k}g)(x)$
for
![]() $n\geqslant N_k$
, every
$n\geqslant N_k$
, every
![]() $g\in \mathrm {Lip}_{0,\mathcal {N}}({\mathbb {H}}^d)$
, and all
$g\in \mathrm {Lip}_{0,\mathcal {N}}({\mathbb {H}}^d)$
, and all
![]() $x\in P_k$
. Using this observation together with the definition of these operators and Remark 5.5, we have
$x\in P_k$
. Using this observation together with the definition of these operators and Remark 5.5, we have
 $$ \begin{align*} (\Phi(\Psi((h_m)_{m\in\mathbb{N}})))_k(x) &= \Big(\Phi\Big(\sum_{m\in\mathbb{N}} E_mh_m\Big)\Big)_k(x) = \sum_{m\in\mathbb{N}}\chi_{1,\ldots,N_k}(E_mh_m)(x) \\ &= \sum_{m\in\mathbb{N}} (\chi_{1,\ldots,N_k} (\chi_{1,\ldots,N_k}^{-1}(h_m))) (x) = \sum_{m\in\mathbb{N}} h_m(x) = h_k(x) \end{align*} $$
$$ \begin{align*} (\Phi(\Psi((h_m)_{m\in\mathbb{N}})))_k(x) &= \Big(\Phi\Big(\sum_{m\in\mathbb{N}} E_mh_m\Big)\Big)_k(x) = \sum_{m\in\mathbb{N}}\chi_{1,\ldots,N_k}(E_mh_m)(x) \\ &= \sum_{m\in\mathbb{N}} (\chi_{1,\ldots,N_k} (\chi_{1,\ldots,N_k}^{-1}(h_m))) (x) = \sum_{m\in\mathbb{N}} h_m(x) = h_k(x) \end{align*} $$
for all
![]() $x\in \mathrm {int}\,(P_k)$
(i.e.
$x\in \mathrm {int}\,(P_k)$
(i.e.
![]() $(\Phi (\Psi ((h_m)_{m\in \mathbb {N}})))_k=h_k$
).
$(\Phi (\Psi ((h_m)_{m\in \mathbb {N}})))_k=h_k$
).
In order to show that
![]() $\Psi \circ \Phi = \mathrm {Id}$
, let
$\Psi \circ \Phi = \mathrm {Id}$
, let
![]() $g\in \mathrm {Lip}_{0,\mathcal {N}}({\mathbb {H}}^d)$
be given. It is enough to check that
$g\in \mathrm {Lip}_{0,\mathcal {N}}({\mathbb {H}}^d)$
be given. It is enough to check that
![]() $\Psi \circ \Phi (g)(x)= g(x)$
for all x in the interior of
$\Psi \circ \Phi (g)(x)= g(x)$
for all x in the interior of
![]() $P_k$
and for all k. Since
$P_k$
and for all k. Since
![]() $\chi _n^{-1}((\Phi (g))_k)(x)$
for
$\chi _n^{-1}((\Phi (g))_k)(x)$
for
![]() $k\neq n$
is only nonzero if
$k\neq n$
is only nonzero if
![]() $x\in H_{n}^+$
and within
$x\in H_{n}^+$
and within
![]() $\varepsilon $
-distance of
$\varepsilon $
-distance of
![]() $H_n$
and there are at most d hyperplanes
$H_n$
and there are at most d hyperplanes
![]() $H_{n_1},\ldots , H_{n_d}$
with this property, there are numbers
$H_{n_1},\ldots , H_{n_d}$
with this property, there are numbers
![]() $M,N\in \mathbb {N}$
such that
$M,N\in \mathbb {N}$
such that

since we may interpret the sum ![]() locally around x as a representation of
locally around x as a representation of
![]() $\chi _{1,\ldots ,N}(g)$
as a function similar to the previous sections, and the operator
$\chi _{1,\ldots ,N}(g)$
as a function similar to the previous sections, and the operator
![]() $\chi _{1,\ldots , N}$
and its inverse are defined pointwise and only depend on “nearby” values of the function.
$\chi _{1,\ldots , N}$
and its inverse are defined pointwise and only depend on “nearby” values of the function.
5.4 Conclusion of the proof and consequences
In this section, we use the arguments of the previous sections and combine them with the results of Section 4 to prove our main result. Moreover, we state a number of direct consequences of the main result and compare it to the case of the space of bounded Lipschitz functions
![]() $\mathrm {Lip}({\mathbb {H}}^d)$
.
$\mathrm {Lip}({\mathbb {H}}^d)$
.
Theorem 5.7 For
![]() $d=2,3,4$
, we have
$d=2,3,4$
, we have
and
Proof We consider the mapping
which by Lemma 5.1, Lemma 5.3, and Proposition 5.6 is a weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous isomorphism. By Lemma 3.1,
$^*$
continuous isomorphism. By Lemma 3.1,
![]() $P_m$
is bi-Lipschitz equivalent to the same polytope
$P_m$
is bi-Lipschitz equivalent to the same polytope
![]() $P_m'$
considered in
$P_m'$
considered in
![]() $\mathbb {R}^d$
. Combining this with Proposition 4.3 implies that
$\mathbb {R}^d$
. Combining this with Proposition 4.3 implies that
![]() $\mathrm {Lip}_{0,S_m}(P_m)$
and
$\mathrm {Lip}_{0,S_m}(P_m)$
and
![]() $\mathrm {Lip}_0(P_m)$
are weak
$\mathrm {Lip}_0(P_m)$
are weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
isomorphic, with a uniform bound on the distortion (because the polytopes
$^*$
isomorphic, with a uniform bound on the distortion (because the polytopes
![]() $P_m$
are mutually isometric). This gives the first of the claims above and shows that the isomorphisms are also weak
$P_m$
are mutually isometric). This gives the first of the claims above and shows that the isomorphisms are also weak
![]() $^*$
-to-weak
$^*$
-to-weak
![]() $^*$
continuous. Hence, we may pass to the preduals and arrive at the second claim.
$^*$
continuous. Hence, we may pass to the preduals and arrive at the second claim.
Corollary 5.8 Let
![]() $d=2,3,4$
and
$d=2,3,4$
and
![]() $\mathcal {M}$
be any net in
$\mathcal {M}$
be any net in
![]() ${\mathbb {H}}^d$
. Then
${\mathbb {H}}^d$
. Then
![]() $\mathcal {F}({\mathbb {H}}^d)$
is isomorphic to
$\mathcal {F}({\mathbb {H}}^d)$
is isomorphic to
![]() $\mathcal {F}(\mathcal {M})\oplus \mathcal {F}(\mathbb {R}^d)$
.
$\mathcal {F}(\mathcal {M})\oplus \mathcal {F}(\mathbb {R}^d)$
.
Proof As proved by Bogopolskii in [Reference Bogopolskii12], all nets in
![]() ${\mathbb {H}}^d$
are bi-Lipschitz equivalent; thus
${\mathbb {H}}^d$
are bi-Lipschitz equivalent; thus
![]() $\mathcal {F}(\mathcal M)\simeq \mathcal {F}(\mathcal N)$
, where
$\mathcal {F}(\mathcal M)\simeq \mathcal {F}(\mathcal N)$
, where
![]() $\mathcal N$
is the net from the above theorem. Moreover, by Lemma 3.1,
$\mathcal N$
is the net from the above theorem. Moreover, by Lemma 3.1,
![]() $P_1$
is bi-Lipschitz equivalent to a polytope in
$P_1$
is bi-Lipschitz equivalent to a polytope in
![]() $\mathbb {R}^d$
(with nonempty interior), so
$\mathbb {R}^d$
(with nonempty interior), so
![]() $\mathcal {F}(P_1)\simeq \mathcal {F}(\mathbb {R}^d)$
due to [Reference Kaufmann36, Corollary 3.5]. Finally, each
$\mathcal {F}(P_1)\simeq \mathcal {F}(\mathbb {R}^d)$
due to [Reference Kaufmann36, Corollary 3.5]. Finally, each
![]() $\mathcal {F}(P_n)$
is isometric to
$\mathcal {F}(P_n)$
is isometric to
![]() $\mathcal {F}(P_1)$
; thus,
$\mathcal {F}(P_1)$
; thus,
![]() $(\bigoplus _n \mathcal {F}(P_n))_{\ell _1} \simeq (\bigoplus _n \mathcal {F}(\mathbb {R}^d))_{\ell _1} \simeq F(\mathbb {R}^d)$
, where the last isomorphism follows from [Reference Kaufmann36, Theorem 3.1].
$(\bigoplus _n \mathcal {F}(P_n))_{\ell _1} \simeq (\bigoplus _n \mathcal {F}(\mathbb {R}^d))_{\ell _1} \simeq F(\mathbb {R}^d)$
, where the last isomorphism follows from [Reference Kaufmann36, Theorem 3.1].
Remark 5.9 Alternatively, instead of [Reference Bogopolskii12], we could have used the following result from [Reference Hájek and Novotný32]: if
![]() $\mathcal {N}$
and
$\mathcal {N}$
and
![]() $\mathcal {M}$
are nets in a metric space, both of cardinality the density of the metric space, then
$\mathcal {M}$
are nets in a metric space, both of cardinality the density of the metric space, then
![]() $\mathcal {F}(\mathcal {N})\simeq \mathcal {F}(\mathcal {M})$
.
$\mathcal {F}(\mathcal {N})\simeq \mathcal {F}(\mathcal {M})$
.
Corollary 5.10 For
![]() $d=2,3,4$
,
$d=2,3,4$
,
![]() $\mathcal {F}({\mathbb {H}}^d)$
has a Schauder basis.
$\mathcal {F}({\mathbb {H}}^d)$
has a Schauder basis.
Proof We will show that
![]() $\mathcal {F}(\mathcal {N})\oplus \mathcal {F}(\mathbb {R}^d)$
has a Schauder basis.
$\mathcal {F}(\mathcal {N})\oplus \mathcal {F}(\mathbb {R}^d)$
has a Schauder basis.
![]() $\mathcal {F}(\mathcal {N})$
does as proved by Doucha and Kaufmann in [Reference Doucha and Kaufmann23], whereas
$\mathcal {F}(\mathcal {N})$
does as proved by Doucha and Kaufmann in [Reference Doucha and Kaufmann23], whereas
![]() $\mathcal {F}(\mathbb {R}^d)$
does by [Reference Hájek and Pernecká33]. Thus, their direct sum has a Schauder basis as well.
$\mathcal {F}(\mathbb {R}^d)$
does by [Reference Hájek and Pernecká33]. Thus, their direct sum has a Schauder basis as well.
Remark 5.11 Note that a similar construction using a tessellation with cubes works in
![]() $\mathbb {R}^d$
. Additionally, if we look at the spaces of bounded Lipschitz functions
$\mathbb {R}^d$
. Additionally, if we look at the spaces of bounded Lipschitz functions
![]() $\mathrm {Lip}(\mathbb {R}^d)$
and
$\mathrm {Lip}(\mathbb {R}^d)$
and
![]() $\mathrm {Lip}({\mathbb {H}}^d)$
rather than the ones which are zero at a given base point, then we can use an analogous construction to the one we employ in Section 5.2 and Section 5.3 to decompose any function
$\mathrm {Lip}({\mathbb {H}}^d)$
rather than the ones which are zero at a given base point, then we can use an analogous construction to the one we employ in Section 5.2 and Section 5.3 to decompose any function
![]() $f\in \mathrm {Lip}({\mathbb {H}}^d)$
and any
$f\in \mathrm {Lip}({\mathbb {H}}^d)$
and any
![]() $g\in \mathrm {Lip}(\mathbb {R}^d)$
into a sequence of bounded Lipschitz functions
$g\in \mathrm {Lip}(\mathbb {R}^d)$
into a sequence of bounded Lipschitz functions
![]() $(f_n)_{n\in \mathbb {N}}$
and
$(f_n)_{n\in \mathbb {N}}$
and
![]() $(g_n)_{n\in \mathbb {N}}$
on the tiles
$(g_n)_{n\in \mathbb {N}}$
on the tiles
![]() $(P_n)_{n\in \mathbb {N}}$
tessellating
$(P_n)_{n\in \mathbb {N}}$
tessellating
![]() ${\mathbb {H}}^d$
and the cubes
${\mathbb {H}}^d$
and the cubes
![]() $(Q_n)_{n\in \mathbb {N}}$
tesselating
$(Q_n)_{n\in \mathbb {N}}$
tesselating
![]() $\mathbb {R}^d$
, respectively. Since the functions in
$\mathbb {R}^d$
, respectively. Since the functions in
![]() $\mathrm {Lip}(\mathbb {R}^{d})$
and
$\mathrm {Lip}(\mathbb {R}^{d})$
and
![]() $\mathrm {Lip}(\mathbb {H}^d)$
are already bounded and functions in
$\mathrm {Lip}(\mathbb {H}^d)$
are already bounded and functions in
![]() $\mathrm {Lip}(M)$
do not require a base point within the domain on which they are zero, removing the values on a net is not needed in this case. Thus, for
$\mathrm {Lip}(M)$
do not require a base point within the domain on which they are zero, removing the values on a net is not needed in this case. Thus, for
![]() $d=2,3,4$
,
$d=2,3,4$
,
where
![]() $S_n$
is defined as in Definition 5.1 and
$S_n$
is defined as in Definition 5.1 and
![]() $T_n$
, analogously, is the union of all boundary (hyper-)surfaces of the (hyper-)cubes
$T_n$
, analogously, is the union of all boundary (hyper-)surfaces of the (hyper-)cubes
![]() $Q_n$
which are supported by a hyperplane which does not separate
$Q_n$
which are supported by a hyperplane which does not separate
![]() $Q_n$
from the origin
$Q_n$
from the origin
![]() $0_{\mathbb {R}^d}$
. Equivalently, the union of all faces of
$0_{\mathbb {R}^d}$
. Equivalently, the union of all faces of
![]() $Q_n$
which contain the point(s) of
$Q_n$
which contain the point(s) of
![]() $Q_n$
that is (are) furthest from the origin.
$Q_n$
that is (are) furthest from the origin.
From this, we are able to obtain that
![]() $\mathrm {Lip}(\mathbb {H}^d)\simeq \mathrm {Lip}(\mathbb {R}^d)$
– this time, in a completely explicit manner.
$\mathrm {Lip}(\mathbb {H}^d)\simeq \mathrm {Lip}(\mathbb {R}^d)$
– this time, in a completely explicit manner.
Indeed, since
![]() $S_n$
is the part of the boundary of
$S_n$
is the part of the boundary of
![]() $P_n$
which is invisible from the origin (i.e., the geodesics connecting a point from
$P_n$
which is invisible from the origin (i.e., the geodesics connecting a point from
![]() $S_n$
with the origin intersect the polytope in other points) an elementary geometric argument shows that it is simply connected. Similarly,
$S_n$
with the origin intersect the polytope in other points) an elementary geometric argument shows that it is simply connected. Similarly,
![]() $T_n$
is a simply connected subset of
$T_n$
is a simply connected subset of
![]() $Q_n$
. It follows that one can find explicit bi-Lipschitz mappings between any pair
$Q_n$
. It follows that one can find explicit bi-Lipschitz mappings between any pair
![]() $(P_n,S_n)$
and
$(P_n,S_n)$
and
![]() $(Q_m,T_m)$
. The only two tiles for which this is not true are the two tiles
$(Q_m,T_m)$
. The only two tiles for which this is not true are the two tiles
![]() $P_1\subset {\mathbb {H}}^d$
and
$P_1\subset {\mathbb {H}}^d$
and
![]() $Q_1\subset \mathbb {R}^d$
which contain their spaces’ respective base points
$Q_1\subset \mathbb {R}^d$
which contain their spaces’ respective base points
![]() $0$
, since those are the only two tiles whose “boundary condition”
$0$
, since those are the only two tiles whose “boundary condition”
![]() $S_n$
is the entire boundary
$S_n$
is the entire boundary
![]() $\partial P_1$
and
$\partial P_1$
and
![]() $\partial Q_1$
, respectively. However, this simply means that we map
$\partial Q_1$
, respectively. However, this simply means that we map
![]() $P_1$
to
$P_1$
to
![]() $Q_1$
in a bi-Lipschitz way, and then carry on with the rest of the sequence arbitrarily since any other
$Q_1$
in a bi-Lipschitz way, and then carry on with the rest of the sequence arbitrarily since any other
![]() $(P_n,S_n)$
can be bi-Lipschitz mapped to any, say,
$(P_n,S_n)$
can be bi-Lipschitz mapped to any, say,
![]() $(Q_m,T_m)$
.
$(Q_m,T_m)$
.
Finally, there are only finitely many different pairs
![]() $(P_n,S_n)$
, which are not pairwise congruent (and similarly, finitely many pairs
$(P_n,S_n)$
, which are not pairwise congruent (and similarly, finitely many pairs
![]() $(Q_m,T_m)$
). Therefore, these bi-Lipschitz maps have uniformly bounded distortion and hence induce and isomorphism
$(Q_m,T_m)$
). Therefore, these bi-Lipschitz maps have uniformly bounded distortion and hence induce and isomorphism
![]() $\mathrm {Lip}(\mathbb {H}^d)\simeq \mathrm {Lip}(\mathbb {R}^d)$
.
$\mathrm {Lip}(\mathbb {H}^d)\simeq \mathrm {Lip}(\mathbb {R}^d)$
.
Remark 5.12 The isomorphism
![]() $\mathrm {Lip}(\mathbb {S}^d)\simeq \mathrm {Lip}(\mathbb {R}^d)$
can be deduced from the corresponding isomorphism for the
$\mathrm {Lip}(\mathbb {S}^d)\simeq \mathrm {Lip}(\mathbb {R}^d)$
can be deduced from the corresponding isomorphism for the
![]() $\mathrm {Lip}_0$
-spaces. First note that since
$\mathrm {Lip}_0$
-spaces. First note that since
![]() $\mathbb {S}^d$
has a finite diameter, the space
$\mathbb {S}^d$
has a finite diameter, the space
![]() $\mathrm {Lip}_0(\mathbb {S}^{d})$
is a hyperplane in
$\mathrm {Lip}_0(\mathbb {S}^{d})$
is a hyperplane in
![]() $\mathrm {Lip}(\mathbb {S}^d)$
. Moreover, we have
$\mathrm {Lip}(\mathbb {S}^d)$
. Moreover, we have
by [Reference Albiac, Ansorena, Cúth and Doucha1] or [Reference Freeman and Gartland25]. As for the sphere, the space
![]() $\mathrm {Lip}_0([0,1]^d)$
is a hyperplane in
$\mathrm {Lip}_0([0,1]^d)$
is a hyperplane in
![]() $\mathrm {Lip}([0,1]^d)$
. By [Reference Cúth, Doucha and Wojtaszczyk20, Theorem 5] all the
$\mathrm {Lip}([0,1]^d)$
. By [Reference Cúth, Doucha and Wojtaszczyk20, Theorem 5] all the
![]() $\mathrm {Lip}_0$
-spaces above and hence also all spaces of bounded Lipschitz functions contain a (complemented) copy of
$\mathrm {Lip}_0$
-spaces above and hence also all spaces of bounded Lipschitz functions contain a (complemented) copy of
![]() $\ell _\infty $
; hence, they are isomorphic to their hyperplanes. Therefore, we may conclude that
$\ell _\infty $
; hence, they are isomorphic to their hyperplanes. Therefore, we may conclude that
![]() $\mathrm {Lip}(\mathbb {S}^{d}) \simeq \mathrm {Lip}([0,1]^d)$
. Using Proposition 4.3 together with an argument similar to the one in Remark 5.11, we obtain that
$\mathrm {Lip}(\mathbb {S}^{d}) \simeq \mathrm {Lip}([0,1]^d)$
. Using Proposition 4.3 together with an argument similar to the one in Remark 5.11, we obtain that
![]() $\mathrm {Lip}(\mathbb {S}^{d})\simeq \mathrm {Lip}(\mathbb {R}^d)$
. In contrast to the case of the hyperbolic space, this argument works for arbitrary d.
$\mathrm {Lip}(\mathbb {S}^{d})\simeq \mathrm {Lip}(\mathbb {R}^d)$
. In contrast to the case of the hyperbolic space, this argument works for arbitrary d.
Acknowledgements
The authors wish to thank Professors Martin Pfurner and Hans-Peter Schröcker for interesting discussions on geometric aspects of this article. We are also grateful to the anonymous referee for the helpful report. The research of C. Bargetz and F. Luggin was supported by the Austrian Science Fund (FWF): I 4570-N. F. Luggin gratefully acknowledges the support by the Vice-Rectorate for Research at the University of Innsbruck in the form of a PhD scholarship.