Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T01:01:53.687Z Has data issue: false hasContentIssue false
  • English
  • Français

Sublinearity and Other Spectral Conditions on a Semigroup

Published online by Cambridge University Press:  20 November 2018

Heydar Radjavi
Heydar Radjavi*
Affiliation:
Dalhousie University, Halifax, Nova Scotia, B3H 3J5
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Subadditivity, sublinearity, submultiplicativity, and other conditions are considered for spectra of pairs of operators on a Hilbert space. Sublinearity, for example, is a weakening of the well-known property 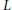$L$ and means 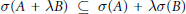$\sigma (A\,+\,\lambda B)\,\subseteq \,\sigma (A)\,+\,\lambda \sigma (B)$ for all scalars 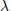$\lambda$. The effect of these conditions is examined on commutativity, reducibility, and triangularizability of multiplicative semigroups of operators. A sample result is that sublinearity of spectra implies simultaneous triangularizability for a semigroup of compact operators.

Keywords

47A1547D0315A3020A2047A1047B10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 1 , 01 February 2000 , pp. 197 - 224
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Frobenius, G., Über vertauschbare Matrizen. Preuss. Akad. Wiss. Sitzungsber (1896), 601–604.Google Scholar
[2] Guralnick, R. M., Triangularization of sets of matrices. Linear and Multilinear Algebra 9 (1980), 133–140.Google Scholar
[3] Hadwin, H., Nordgren, E., Radjabalipour, M., Radjavi, H. and Rosenthal, P., A nil algebra of bounded operators on Hilbert space with semisimple norm closure. Integral Equations Operator Theory 9 (1986), 239–243.Google Scholar
[4] Kaplansky, I., Completely continuous normal operators with property L. Pacific J. Math. 3 (1953), 721–724.Google Scholar
[5] Lambrou, M., Longstaff, W. and Radjavi, H., Spectral conditions and reducibility of operator semigroups. Indiana University Math. J. 41 (1992), 449–464.Google Scholar
[6] Laurie, C., Nordgren, E., Radjavi, H. and Rosenthal, P., On triangularization of algebras of operators. J. Reine Angew Math. 327 (1981), 143–155.Google Scholar
[7] Levitzki, J., Ü ber nilpotente Unterringe.Math. Ann. 105 (1931), 620–627.Google Scholar
[8] Lomonosov, V. I., Invariant subspaces of operators commuting with compact operators. Functional Anal. Appl. 7 (1973), 213–214.Google Scholar
[9] Mc Coy, N. H., On the characteristic roots of matrix polynomials. Bull. Amer. Math. Soc. 42 (1936), 592–600.Google Scholar
[10] Motzkin, T. S. and Taussky, O., Pairs of matrices with property L. Trans. Amer. Math. Soc. 73 (1952), 108–114.Google Scholar
[11] Motzkin, T. S. and Taussky, O., On representations of finite groups. Nederl. Akad. Wetensch. Proc. Ser. A 55 —Indagationes Math. 14 (1952), 511–512.Google Scholar
[12] Nordgren, E., Radjavi, H. and Rosenthal, P., Triangularizing semigroups of compact operators. Indiana University Math. J. 33 (1984), 271–275.Google Scholar
[13] Radjabalipour, M. and Radjavi, H., A finiteness lemma, Brauer's theorem and other irreducibility results. Comm. Algebra 27 (1999), 301–319.Google Scholar
[14] Radjavi, H., A trace condition equivalent to simultaneous triangularizability. Canad. J. Math. 38 (1986), 376–386.Google Scholar
[15] Radjavi, H., On reducibility of semigroups of compact operators. Indiana University Math. J. 39 (1990), 499–515.Google Scholar
[16] Radjavi, H. and Rosenthal, P., From local to global triangularization. J. Funct. Anal. 147 (1997), 443–456.Google Scholar
[17] Radjavi, H., Rosenthal, P. and Shulman, V., Operator semigroups with nilpotent commutators. Proc. Amer. Math. Soc., to appear.Google Scholar
[18] Ringrose, J. R., Super-diagonal forms for compact linear operators. Proc. London Math. Soc. 12 (1962), 367–384.Google Scholar
[19] Schmidt, O. J., Über Gruppen, deren s ämtliche Teiler spezielle Gruppen sind. Math. Sbornik 31 (1924), 366–372.Google Scholar
[20] Serre, J. P., Linear Representations of Finite Groups. Springer-Verlag, New York, 1977.Google Scholar
[21] Turovskii, Yu. V., Volterra semigroups have invariant subspaces. J. Funct. Anal. 162 (1999), 313–322.Google Scholar
[22] Wales, D. B. and Zassenhaus, H. J., On L-groups. Math. Ann. 198 (1972), 1–12.Google Scholar
[23] Wiegmann, N. A., A note on pairs of normal matrices with property L. Proc. Amer. Math. Soc. 4 (1953), 35–36.Google Scholar
[24] Wielandt, W., Lineare Scharen von Matrizen mit reellen Eigenwerten. Math. Zeit. 53 (1950), 219–225.Google Scholar
[25] Zaussenhaus, H. J., On L-semigroups. Math. Ann. 198 (1972), 13–22.Google Scholar