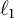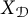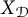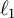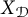1 Introduction
In Banach space theory, an asymptotic notion refers to a concept describing the behavior of the norm of linear combinations of vectors sampled in a specified asymptotic fashion from a certain type of structure. For example, the seminal notion of a spreading model of a bounded sequence
![]() $(x_n)_{n=1}^\infty $
is defined as the unit vector basis
$(x_n)_{n=1}^\infty $
is defined as the unit vector basis
![]() $(e_i)_{i=1}^\infty $
of
$(e_i)_{i=1}^\infty $
of
![]() $c_{00}$
with the seminorm given by
$c_{00}$
with the seminorm given by
 $$\begin{align*}\Big|\sum_{i=1}^na_i e_i\Big| = \lim_{k_1\to\infty}\lim_{k_{2}\to\infty}\cdots\lim_{k_n\to\infty}\Big\|\sum_{i=1}^na_ix_{k_i}\Big\|,\end{align*}$$
$$\begin{align*}\Big|\sum_{i=1}^na_i e_i\Big| = \lim_{k_1\to\infty}\lim_{k_{2}\to\infty}\cdots\lim_{k_n\to\infty}\Big\|\sum_{i=1}^na_ix_{k_i}\Big\|,\end{align*}$$
provided that this iterated limit exists for all choices of coefficients
![]() $a_1,\ldots ,a_n$
. Here, the structure in question is a bounded sequence of vectors in a Banach space, and vectors are sampled over a sparse set of sufficiently large indices. Using Ramsey’s Theorem, Brunel and Sucheston proved in [Reference Brunel and Sucheston9] that every bounded sequence in a Banach space has a subsequence generating some spreading model. Similar notions about different types of structures have been introduced and studied over the years. One such example is the notion of asymptotic models, introduced by Odell and Halbeisen in [Reference Halbeisen and Odell13], concerning the norm of linear combinations of vectors sampled from an array of sequences. A different type of such a notion is asymptotic spaces, introduced by Maurey, Milman, and Tomczak-Jaegerman in [Reference Maurey, Milman and Tomczak-Jaegermann17], concerning the norm of linear combinations of vectors picked in a finite-round two-player game between a vector chooser and a finite-codimensional subspace chooser. The different types of asymptotic notions are relevant to the study of many subjects in Banach space theory, such as the distortion problem in [Reference Milman and Tomczak-Jaegermann18] using asymptotic spaces, the invariant subspace problem in reflexive Banach spaces in [Reference Argyros and Motakis4] using spreading models, the uniform approximation properties of bounded linear operators in [Reference Argyros, Georgiou, Lagos and Motakis2] using joint spreading models, the coarse geometry of Banach spaces in [Reference Baudier, Lancien, Motakis and Schlumprecht7] using asymptotic models, unique maximal ideals in the operators of stopping time-type Banach spaces in [Reference Kania and Lechner16] using spreading models, and quotients algebras of operator spaces in [Reference Motakis and Pelczar-Barwacz20] using asymptotic versions. The wide applicability of these tools has led to an independent study of their uniqueness properties and a desire to better understand their interconnections. Among the most outspoken promoters of this program was Odell, who in this context posed several questions of the following type (see [Reference Odell22], [Reference Odell23], and [Reference Junge, Kutzarova and Odell15]): Let P, Q be properties of Banach spaces that are stable under passing to closed subspaces and assume that P implies Q. If a Banach space X satisfies Q, must it have an infinite-dimensional closed subspace satisfying P? For such P and Q, if there exists a Banach space X satisfying Q and all infinite-dimensional subspaces of which fail P, then we say that P is completely separated from Q. For a detailed discussion on positive and negative results in this context, we refer the reader to [Reference Argyros and Motakis5]. We prove such a complete separation theorem for P the Lebesgue property and Q the property of admitting a unique
$a_1,\ldots ,a_n$
. Here, the structure in question is a bounded sequence of vectors in a Banach space, and vectors are sampled over a sparse set of sufficiently large indices. Using Ramsey’s Theorem, Brunel and Sucheston proved in [Reference Brunel and Sucheston9] that every bounded sequence in a Banach space has a subsequence generating some spreading model. Similar notions about different types of structures have been introduced and studied over the years. One such example is the notion of asymptotic models, introduced by Odell and Halbeisen in [Reference Halbeisen and Odell13], concerning the norm of linear combinations of vectors sampled from an array of sequences. A different type of such a notion is asymptotic spaces, introduced by Maurey, Milman, and Tomczak-Jaegerman in [Reference Maurey, Milman and Tomczak-Jaegermann17], concerning the norm of linear combinations of vectors picked in a finite-round two-player game between a vector chooser and a finite-codimensional subspace chooser. The different types of asymptotic notions are relevant to the study of many subjects in Banach space theory, such as the distortion problem in [Reference Milman and Tomczak-Jaegermann18] using asymptotic spaces, the invariant subspace problem in reflexive Banach spaces in [Reference Argyros and Motakis4] using spreading models, the uniform approximation properties of bounded linear operators in [Reference Argyros, Georgiou, Lagos and Motakis2] using joint spreading models, the coarse geometry of Banach spaces in [Reference Baudier, Lancien, Motakis and Schlumprecht7] using asymptotic models, unique maximal ideals in the operators of stopping time-type Banach spaces in [Reference Kania and Lechner16] using spreading models, and quotients algebras of operator spaces in [Reference Motakis and Pelczar-Barwacz20] using asymptotic versions. The wide applicability of these tools has led to an independent study of their uniqueness properties and a desire to better understand their interconnections. Among the most outspoken promoters of this program was Odell, who in this context posed several questions of the following type (see [Reference Odell22], [Reference Odell23], and [Reference Junge, Kutzarova and Odell15]): Let P, Q be properties of Banach spaces that are stable under passing to closed subspaces and assume that P implies Q. If a Banach space X satisfies Q, must it have an infinite-dimensional closed subspace satisfying P? For such P and Q, if there exists a Banach space X satisfying Q and all infinite-dimensional subspaces of which fail P, then we say that P is completely separated from Q. For a detailed discussion on positive and negative results in this context, we refer the reader to [Reference Argyros and Motakis5]. We prove such a complete separation theorem for P the Lebesgue property and Q the property of admitting a unique
![]() $\ell _1$
spreading model.
$\ell _1$
spreading model.
Let X be a Banach space. A function
![]() $f:[0,1]\to X$
is Riemann-integrable if it is bounded and continuous up to a set of Lebesgue measure zero (see, for example, [Reference Gordon12, Theorem 18] or [Reference Gaebler10, Theorem. 2.1.3.]). However, the converse statement is false in general. Indeed, it is easy to check that the function which maps the rationals in
$f:[0,1]\to X$
is Riemann-integrable if it is bounded and continuous up to a set of Lebesgue measure zero (see, for example, [Reference Gordon12, Theorem 18] or [Reference Gaebler10, Theorem. 2.1.3.]). However, the converse statement is false in general. Indeed, it is easy to check that the function which maps the rationals in
![]() $[0,1]$
to the unit vector basis of
$[0,1]$
to the unit vector basis of
![]() $c_{0}$
is Riemann-integrable. A Banach space X is therefore said to have the Lebesgue property if every Riemann-integrable function
$c_{0}$
is Riemann-integrable. A Banach space X is therefore said to have the Lebesgue property if every Riemann-integrable function
![]() $f:[0,1]\to X$
is continuous up to a set of Lebesgue measure zero. The first and third named authors recently in [Reference Gaebler and Sari11] characterized the Lebesgue property in terms of a new asymptotic notion. In particular, a Banach space X has the Lebesgue property if and only if every normalized basic sequence in X is Haar-
$f:[0,1]\to X$
is continuous up to a set of Lebesgue measure zero. The first and third named authors recently in [Reference Gaebler and Sari11] characterized the Lebesgue property in terms of a new asymptotic notion. In particular, a Banach space X has the Lebesgue property if and only if every normalized basic sequence in X is Haar-
![]() $\ell _{1}^{+}$
(see [Reference Gaebler and Sari11] or Section 2 of this paper for the precise definition of Haar-
$\ell _{1}^{+}$
(see [Reference Gaebler and Sari11] or Section 2 of this paper for the precise definition of Haar-
![]() $\ell _{1}^{+}$
). It is also proved in [Reference Gaebler and Sari11] that for the properties
$\ell _{1}^{+}$
). It is also proved in [Reference Gaebler and Sari11] that for the properties
-
(P1) every asymptotic model of X is equivalent to the unit vector basis of
 $\ell _{1}$
,
$\ell _{1}$
, -
(P2) X satisfies the Lebesgue property,
-
(P3) every spreading model of X is equivalent to the unit vector basis of
 $\ell _{1}$
$\ell _{1}$
the implications (P1)
![]() $\implies $
(P2)
$\implies $
(P2)
![]() $\implies $
(P3) are true. However, (P2)
$\implies $
(P3) are true. However, (P2)![]() (P1) because the Tsirelson sum of Tsirelson spaces,
(P1) because the Tsirelson sum of Tsirelson spaces,
![]() $(T\oplus T\oplus \ldots )_{T}$
, has the Lebesgue property but no unique asymptotic model (see, for example, [Reference Gaebler and Sari11]) and (P3)
$(T\oplus T\oplus \ldots )_{T}$
, has the Lebesgue property but no unique asymptotic model (see, for example, [Reference Gaebler and Sari11]) and (P3)![]() (P2) because there exist Schur spaces that do not have the Lebesgue property (e.g. [Reference Haydon14],[Reference Naralenkov21]) and Schur spaces satisfy (P3). The complete separation of (P1) from (P2) was proved in [Reference Gaebler and Sari11] by showing that the Banach space
(P2) because there exist Schur spaces that do not have the Lebesgue property (e.g. [Reference Haydon14],[Reference Naralenkov21]) and Schur spaces satisfy (P3). The complete separation of (P1) from (P2) was proved in [Reference Gaebler and Sari11] by showing that the Banach space
![]() $X_{iw}$
constructed in [Reference Argyros and Motakis5] has the Lebesgue property, and yet, every subspace of
$X_{iw}$
constructed in [Reference Argyros and Motakis5] has the Lebesgue property, and yet, every subspace of
![]() $X_{iw}$
contains a
$X_{iw}$
contains a
![]() $c_{0}$
-asymptotic model. The complete separation of (P2) from (P3) was not attempted in [Reference Gaebler and Sari11], and it is the purpose of the present article. By carrying out a substantial modification of the construction in [Reference Argyros and Motakis5], we are able to achieve this new result. We construct a Banach space
$c_{0}$
-asymptotic model. The complete separation of (P2) from (P3) was not attempted in [Reference Gaebler and Sari11], and it is the purpose of the present article. By carrying out a substantial modification of the construction in [Reference Argyros and Motakis5], we are able to achieve this new result. We construct a Banach space
![]() $X_{\mathcal {D}}$
with an unconditional basis such that every spreading model of
$X_{\mathcal {D}}$
with an unconditional basis such that every spreading model of
![]() $X_{\mathcal {D}}$
is uniformly equivalent to the unit vector basis of
$X_{\mathcal {D}}$
is uniformly equivalent to the unit vector basis of
![]() $\ell _{1}$
and such that every subspace of
$\ell _{1}$
and such that every subspace of
![]() $X_{\mathcal {D}}$
fails the Lebesgue property.
$X_{\mathcal {D}}$
fails the Lebesgue property.
Let us explain the main properties of
![]() $X_{\mathcal {D}}$
. Denote by
$X_{\mathcal {D}}$
. Denote by
![]() $\mathcal {D}$
the binary tree
$\mathcal {D}$
the binary tree
![]() $\cup _{n=0}^\infty \{0,1\}^n$
. Following standard convention,
$\cup _{n=0}^\infty \{0,1\}^n$
. Following standard convention,
![]() $\{0,1\}^0$
is a singleton containing the empty sequence. For
$\{0,1\}^0$
is a singleton containing the empty sequence. For
![]() $n\in \mathbb {N}\cup \{0\}$
and
$n\in \mathbb {N}\cup \{0\}$
and
![]() $\lambda \in \{0,1\}^n$
, we write
$\lambda \in \{0,1\}^n$
, we write
![]() $|\lambda | = n$
and say
$|\lambda | = n$
and say
![]() $\lambda $
has height n. We consider
$\lambda $
has height n. We consider
![]() $\mathcal {D}$
with the usual partial order with minimum the empty sequence, and, otherwise,
$\mathcal {D}$
with the usual partial order with minimum the empty sequence, and, otherwise,
![]() $\lambda \leq \mu $
means
$\lambda \leq \mu $
means
![]() $|\lambda |\leq |\mu |$
and
$|\lambda |\leq |\mu |$
and
![]() $\lambda (i) = \mu (i)$
, for
$\lambda (i) = \mu (i)$
, for
![]() $1\leq i\leq |\lambda |$
. The characterization of the Lebesgue property in terms of Haar-
$1\leq i\leq |\lambda |$
. The characterization of the Lebesgue property in terms of Haar-
![]() $\ell _1^+$
sequences from [Reference Gaebler and Sari11] easily yields the following (see Remark 2.2): a Banach space X has the Lebesgue property if and only if, for every collection
$\ell _1^+$
sequences from [Reference Gaebler and Sari11] easily yields the following (see Remark 2.2): a Banach space X has the Lebesgue property if and only if, for every collection
![]() $(x_\lambda )_{\lambda \in \mathcal {D}}$
of norm-one vectors in X, there exists a constant
$(x_\lambda )_{\lambda \in \mathcal {D}}$
of norm-one vectors in X, there exists a constant
![]() $\theta>0$
such that, for every
$\theta>0$
such that, for every
![]() $n\in \mathbb {N}$
, there exists a subset
$n\in \mathbb {N}$
, there exists a subset
![]() $V\subset \{0,1\}^{n}$
such that
$V\subset \{0,1\}^{n}$
such that
 $$ \begin{align*}\theta\leq \frac{1}{2^{n}}\left\Vert\sum_{\lambda\in V} x_{\mu_{\lambda}}\right\Vert \end{align*} $$
$$ \begin{align*}\theta\leq \frac{1}{2^{n}}\left\Vert\sum_{\lambda\in V} x_{\mu_{\lambda}}\right\Vert \end{align*} $$
for some choice of nodes
![]() $(\mu _{\lambda })_{\lambda \in V}$
with
$(\mu _{\lambda })_{\lambda \in V}$
with
![]() $\mu _{\lambda }\geq \lambda $
. In the space
$\mu _{\lambda }\geq \lambda $
. In the space
![]() $X_{\mathcal {D}}$
, every infinite-dimensional subspace contains a lexicographically block collection
$X_{\mathcal {D}}$
, every infinite-dimensional subspace contains a lexicographically block collection
![]() $(x_\lambda )_{{\lambda \in \mathcal {D}}}$
of norm-one vectors such that for any
$(x_\lambda )_{{\lambda \in \mathcal {D}}}$
of norm-one vectors such that for any
![]() $n\in \mathbb {N}$
and collection
$n\in \mathbb {N}$
and collection
![]() $(\mu _\lambda )_{\lambda \in \{0,1\}^n}$
in
$(\mu _\lambda )_{\lambda \in \{0,1\}^n}$
in
![]() $\mathcal {D}$
such that
$\mathcal {D}$
such that
![]() $\mu _\lambda \geq \lambda $
,
$\mu _\lambda \geq \lambda $
,
![]() $\lambda \in \{0,1\}^n$
,
$\lambda \in \{0,1\}^n$
,
for any scalars
![]() $(a_\lambda )_{{\lambda \in \{0,1\}^n}}$
. Therefore,
$(a_\lambda )_{{\lambda \in \{0,1\}^n}}$
. Therefore,
![]() $X_{\mathcal {D}}$
fails the Lebesgue property. At the same time, every normalized weakly null sequence in
$X_{\mathcal {D}}$
fails the Lebesgue property. At the same time, every normalized weakly null sequence in
![]() $X_{\mathcal {D}}$
has a subsequence generating a spreading model that is
$X_{\mathcal {D}}$
has a subsequence generating a spreading model that is
![]() $102$
-equivalent to the unit vector basis of
$102$
-equivalent to the unit vector basis of
![]() $\ell _1$
. In particular, it follows from James’s characterization of reflexivity for spaces with an unconditional basis that
$\ell _1$
. In particular, it follows from James’s characterization of reflexivity for spaces with an unconditional basis that
![]() $X_{\mathcal {D}}$
is reflexive.
$X_{\mathcal {D}}$
is reflexive.
Our construction relies on the method of saturation under constraints with increasing weights, also employed in [Reference Argyros and Motakis5]. The major difference lies in the involvement of an additional metric constraint. A distantly related version of this constraint was also present in [Reference Motakis19], but its application and role were significantly different as it produced an operator-algebraic outcome (see [Reference Motakis19, Section 2]). The earliest form of saturation under constraints is due to Odell and Schlumprecht (see [Reference Odell and Schlumprecht24] and [Reference Odell and Schlumprecht25]). It has since been extensively developed – for example, in the papers [Reference Argyros and Motakis4], [Reference Beanland, Freeman and Motakis8], [Reference Argyros and Motakis5], and many others. Let us elaborate on the main ingredients of our construction. The norm of the space
![]() $X_{\mathcal {D}}$
is defined via a norming set; that is, there is a subset W of
$X_{\mathcal {D}}$
is defined via a norming set; that is, there is a subset W of
![]() $c_{00}$
containing the unit vector basis
$c_{00}$
containing the unit vector basis
![]() $(e_i^*)_{i=1}^\infty $
such that, for
$(e_i^*)_{i=1}^\infty $
such that, for
![]() $x\in c_{00}$
,
$x\in c_{00}$
,
![]() $\|x\| = \sup \{|\langle f,x\rangle |:f\in W\}$
, where
$\|x\| = \sup \{|\langle f,x\rangle |:f\in W\}$
, where
![]() $\langle \cdot ,\cdot \rangle $
denotes the standard duality pairing of
$\langle \cdot ,\cdot \rangle $
denotes the standard duality pairing of
![]() $c_{00}\times c_{00}$
. The space
$c_{00}\times c_{00}$
. The space
![]() $X_{\mathcal {D}}$
is the completion of
$X_{\mathcal {D}}$
is the completion of
![]() $c_{00}$
under this norm. We fix a pair of lacunary sequences
$c_{00}$
under this norm. We fix a pair of lacunary sequences
![]() $m_j$
,
$m_j$
,
![]() $n_j$
,
$n_j$
,
![]() $j\in \mathbb {N}$
, of natural numbers. The first sequence is used to define a collection of weights
$j\in \mathbb {N}$
, of natural numbers. The first sequence is used to define a collection of weights
![]() $\{\prod _{i=1}^\ell m_{j_i}:j_1,\ldots ,j_\ell \in \mathbb {N}\}$
, which is closed under multiplication. To each weight
$\{\prod _{i=1}^\ell m_{j_i}:j_1,\ldots ,j_\ell \in \mathbb {N}\}$
, which is closed under multiplication. To each weight
![]() $\prod _{i=1}^\ell m_{j_i}$
, we associate a Schreier family
$\prod _{i=1}^\ell m_{j_i}$
, we associate a Schreier family
![]() $\mathcal {S}_{n_{j_1}+n_{j_2}+\cdots +n_{j_\ell }}$
. This is a compact collection of finite subsets of
$\mathcal {S}_{n_{j_1}+n_{j_2}+\cdots +n_{j_\ell }}$
. This is a compact collection of finite subsets of
![]() $\mathbb {N}$
recalled in Section 2. Every f in W satisfies
$\mathbb {N}$
recalled in Section 2. Every f in W satisfies
![]() $\|f\|_\infty \leq 1$
, and it is either of the form
$\|f\|_\infty \leq 1$
, and it is either of the form
![]() $\pm e_i^*$
or
$\pm e_i^*$
or
 $$ \begin{align} f = \frac{1}{w(f)}\sum_{q=1}^d f_q, \end{align} $$
$$ \begin{align} f = \frac{1}{w(f)}\sum_{q=1}^d f_q, \end{align} $$
where
![]() $w(f) = \prod _{i=1}^\ell m_{j_i}$
and
$w(f) = \prod _{i=1}^\ell m_{j_i}$
and
![]() $f_1,\ldots ,f_d$
are successively supported vectors such that the set
$f_1,\ldots ,f_d$
are successively supported vectors such that the set
![]() $\{\min \mathrm {supp}(f_q):1\leq q\leq d\}$
is in the collection
$\{\min \mathrm {supp}(f_q):1\leq q\leq d\}$
is in the collection
![]() $\mathcal {S}_{n_{j_1}+n_{j_2}+\cdots +n_{j_d}}$
. A Banach space defined by a norming set on which only the aforementioned restrictions are imposed is asymptotic-
$\mathcal {S}_{n_{j_1}+n_{j_2}+\cdots +n_{j_d}}$
. A Banach space defined by a norming set on which only the aforementioned restrictions are imposed is asymptotic-
![]() $\ell _1$
(see, for example, [Reference Argyros and Deliyanni1]), an asymptotic property implying having a unique
$\ell _1$
(see, for example, [Reference Argyros and Deliyanni1]), an asymptotic property implying having a unique
![]() $\ell _1$
asymptotic model and thus also the Lebesgue property. To avoid this without compromising the uniform uniqueness of
$\ell _1$
asymptotic model and thus also the Lebesgue property. To avoid this without compromising the uniform uniqueness of
![]() $\ell _1$
spreading models, just as in [Reference Argyros and Motakis5], we additionally demand that for f in W as in (1.2), the sequence
$\ell _1$
spreading models, just as in [Reference Argyros and Motakis5], we additionally demand that for f in W as in (1.2), the sequence
![]() $w(f_1),\ldots ,w(f_d)$
is increasing sufficiently rapidly in relation to the supports of
$w(f_1),\ldots ,w(f_d)$
is increasing sufficiently rapidly in relation to the supports of
![]() $f_1$
,…,
$f_1$
,…,
![]() $f_d$
. Imposing these additional restrictions on W yields a Banach space with a uniformly unique
$f_d$
. Imposing these additional restrictions on W yields a Banach space with a uniformly unique
![]() $\ell _1$
spreading model and no asymptotic-
$\ell _1$
spreading model and no asymptotic-
![]() $\ell _1$
subspace; however, as it was proved in [Reference Gaebler and Sari11], it still satisfies the Lebesgue property. The intuitive explanation for this is the following: despite the imposed restrictions on W, there are sufficiently many functionals yielding the required
$\ell _1$
subspace; however, as it was proved in [Reference Gaebler and Sari11], it still satisfies the Lebesgue property. The intuitive explanation for this is the following: despite the imposed restrictions on W, there are sufficiently many functionals yielding the required
![]() $\ell _1^+$
estimates on normalized collections
$\ell _1^+$
estimates on normalized collections
![]() $(x_\lambda )_{\lambda \in \mathcal {D}}$
in the defined Banach space.
$(x_\lambda )_{\lambda \in \mathcal {D}}$
in the defined Banach space.
To address this, we impose an additional metric constraint on W. Recall that
![]() $\mathcal {D}$
is a totally bounded metric space with the metric
$\mathcal {D}$
is a totally bounded metric space with the metric
![]() $d(\lambda ,\mu ) = 2^{-n}$
, where, if
$d(\lambda ,\mu ) = 2^{-n}$
, where, if
![]() $\lambda \neq \mu $
,
$\lambda \neq \mu $
,
![]() $n\in \mathbb {N}\cup \{0\}$
is the maximum height for which there exists
$n\in \mathbb {N}\cup \{0\}$
is the maximum height for which there exists
![]() $\nu \in \{0,1\}^n$
with
$\nu \in \{0,1\}^n$
with
![]() $\nu \leq \lambda $
and
$\nu \leq \lambda $
and
![]() $\nu \leq \mu $
. We fix a bijection
$\nu \leq \mu $
. We fix a bijection
![]() $\phi :\{m_j:j\in \mathbb {N}\}\to \mathcal {D}$
, and to every
$\phi :\{m_j:j\in \mathbb {N}\}\to \mathcal {D}$
, and to every
![]() $f\in W$
of weight
$f\in W$
of weight
![]() $\prod _{i=1}^\ell m_{j_i}$
, we associate the node
$\prod _{i=1}^\ell m_{j_i}$
, we associate the node
![]() $\lambda = \phi (m(f))$
, where
$\lambda = \phi (m(f))$
, where
![]() $m(f)$
is the maximum of
$m(f)$
is the maximum of
![]() $m_{j_1},\ldots ,m_{j_\ell }$
. We then impose on W the restriction that for every f as in (1.2), the nodes
$m_{j_1},\ldots ,m_{j_\ell }$
. We then impose on W the restriction that for every f as in (1.2), the nodes
![]() $\phi (m(f_1)),\ldots ,\phi (m(f_d))$
approximate some
$\phi (m(f_1)),\ldots ,\phi (m(f_d))$
approximate some
![]() $\lambda $
in the completion of
$\lambda $
in the completion of
![]() $\mathcal {D}$
, and the quantification of the approximation depends on the tuple
$\mathcal {D}$
, and the quantification of the approximation depends on the tuple
![]() $(n_{j_1},\ldots , n_{j_\ell })$
and the supports of the
$(n_{j_1},\ldots , n_{j_\ell })$
and the supports of the
![]() $f_q$
,
$f_q$
,
![]() $1\leq q\leq d$
. Modulo some subtle but significant details, the construction of the space
$1\leq q\leq d$
. Modulo some subtle but significant details, the construction of the space
![]() $X_{\mathcal {D}}$
is complete.
$X_{\mathcal {D}}$
is complete.
Using a standard technique, in every block-subspace Y of
![]() $X_{\mathcal {D}}$
, we build a collection of vectors
$X_{\mathcal {D}}$
, we build a collection of vectors
![]() $(x_{m_j})_{j\in \mathbb {N}}$
such that, for every
$(x_{m_j})_{j\in \mathbb {N}}$
such that, for every
![]() $j\in \mathbb {N}$
, the norm of
$j\in \mathbb {N}$
, the norm of
![]() $x_{m_j}$
can only be effectively estimated by functionals of weight
$x_{m_j}$
can only be effectively estimated by functionals of weight
![]() $w(f) = m_j$
; that is,
$w(f) = m_j$
; that is,
![]() $x_{m_j}$
is an exact vector. We then consider the
$x_{m_j}$
is an exact vector. We then consider the
![]() $\mathcal {D}$
-indexed collection
$\mathcal {D}$
-indexed collection
![]() $(x_{\phi ^{-1}(\lambda )})_{\lambda \in \mathcal {D}}$
. This witnesses the failure of the Lebesgue property in Y. Indeed, for
$(x_{\phi ^{-1}(\lambda )})_{\lambda \in \mathcal {D}}$
. This witnesses the failure of the Lebesgue property in Y. Indeed, for
![]() $n\in \mathbb {N}$
, denote
$n\in \mathbb {N}$
, denote
![]() $\{0,1\}^n = \{\lambda _1,\ldots ,\lambda _{2^n}\}$
and let
$\{0,1\}^n = \{\lambda _1,\ldots ,\lambda _{2^n}\}$
and let
![]() $m_{j_1}$
,…,
$m_{j_1}$
,…,
![]() $m_{j_{2^n}}$
such that
$m_{j_{2^n}}$
such that
![]() $\phi (m_{j_1}) \geq \lambda _1$
,…,
$\phi (m_{j_1}) \geq \lambda _1$
,…,
![]() $\phi (m_{j_{2^n}})\geq \lambda _{2^n}$
. Then the nodes
$\phi (m_{j_{2^n}})\geq \lambda _{2^n}$
. Then the nodes
![]() $\phi (m_{j_1})$
,…
$\phi (m_{j_1})$
,…
![]() $\phi (m_{j_{2^n}})$
form a
$\phi (m_{j_{2^n}})$
form a
![]() $2^{-n}$
separated set in
$2^{-n}$
separated set in
![]() $\mathcal {D}$
. For every
$\mathcal {D}$
. For every
![]() $f\in W$
as in (1.2),
$f\in W$
as in (1.2),
![]() $\phi (m(f_1))$
,…,
$\phi (m(f_1))$
,…,
![]() $\phi (m(f_d))$
approximate a
$\phi (m(f_d))$
approximate a
![]() $\lambda $
in the completion of
$\lambda $
in the completion of
![]() $\mathcal {D}$
, and thus, roughly speaking, the components of f only contribute to the norm of very few of the
$\mathcal {D}$
, and thus, roughly speaking, the components of f only contribute to the norm of very few of the
![]() $x_{m_{j_i}}$
,
$x_{m_{j_i}}$
,
![]() $1\leq i\leq 2^n$
, yielding the
$1\leq i\leq 2^n$
, yielding the
![]() $\ell _\infty $
-estimate (1.1).
$\ell _\infty $
-estimate (1.1).
Our paper is organized as follows. In Section 2, we recall the required terminology surrounding Schreier families and special convex combinations. We also recall the definition of a Haar-
![]() $\ell _1^+$
sequence and remark on the formulation of the Lebesgue property in terms of normalized collections
$\ell _1^+$
sequence and remark on the formulation of the Lebesgue property in terms of normalized collections
![]() $(x_\lambda )_{\lambda \in \mathcal {D}}$
. In Section 3, we define the space
$(x_\lambda )_{\lambda \in \mathcal {D}}$
. In Section 3, we define the space
![]() $X_{\mathcal {D}}$
and prove the uniform uniqueness of
$X_{\mathcal {D}}$
and prove the uniform uniqueness of
![]() $\ell _1$
spreading models. In Section 4, we define an auxiliary Banach space
$\ell _1$
spreading models. In Section 4, we define an auxiliary Banach space
![]() $X_{\mathcal {D}}^{\mathrm {aux},\delta }$
and prove
$X_{\mathcal {D}}^{\mathrm {aux},\delta }$
and prove
![]() $\ell _\infty $
-type estimates for linear combinations of “simple” vectors in this space. In Section 5, we define and study rapidly increasing sequences (RISs) and the basic inequality. The former comprise a special class of sequences in
$\ell _\infty $
-type estimates for linear combinations of “simple” vectors in this space. In Section 5, we define and study rapidly increasing sequences (RISs) and the basic inequality. The former comprise a special class of sequences in
![]() $X_{\mathcal {D}}$
, and the latter provides bounds for their linear combinations in terms of linear combinations of basis vectors in the auxiliary space. In Section 6, we combine all ingredients prepared in Sections 4 and 5 to construct in every infinite-dimensional closed subspace of
$X_{\mathcal {D}}$
, and the latter provides bounds for their linear combinations in terms of linear combinations of basis vectors in the auxiliary space. In Section 6, we combine all ingredients prepared in Sections 4 and 5 to construct in every infinite-dimensional closed subspace of
![]() $X_{\mathcal {D}}$
a normalized collection
$X_{\mathcal {D}}$
a normalized collection
![]() $(x_\lambda )_{\lambda \in \mathcal {D}}$
witnessing the failure of the Lebesgue property.
$(x_\lambda )_{\lambda \in \mathcal {D}}$
witnessing the failure of the Lebesgue property.
2 Preliminary information
Let
![]() $A,B\subset \mathbb {N}$
. If
$A,B\subset \mathbb {N}$
. If
![]() $\max (A)<\min (B)$
, then we write
$\max (A)<\min (B)$
, then we write
![]() $A<B$
. We also write
$A<B$
. We also write
![]() $n\leq A$
if
$n\leq A$
if
![]() $n\in \mathbb {N}$
is at most
$n\in \mathbb {N}$
is at most
![]() $\min (A)$
and, by convention,
$\min (A)$
and, by convention,
![]() $\emptyset <A$
and
$\emptyset <A$
and
![]() $A<\emptyset $
for every
$A<\emptyset $
for every
![]() $A\subset \mathbb {N}$
. We denote by
$A\subset \mathbb {N}$
. We denote by
![]() $c_{00}$
the vector space that consists of sequences of real numbers that have at most finitely-many nonzero terms, and we let
$c_{00}$
the vector space that consists of sequences of real numbers that have at most finitely-many nonzero terms, and we let
![]() $(e_{i})$
be the unit vector basis of
$(e_{i})$
be the unit vector basis of
![]() $c_{00}$
. Note that the members of the norming set W are themselves members of
$c_{00}$
. Note that the members of the norming set W are themselves members of
![]() $c_{00}$
and, in particular, that
$c_{00}$
and, in particular, that
![]() $\{\pm e_{i}\}_{i=1}^{\infty }\subset W$
. For this reason, we write
$\{\pm e_{i}\}_{i=1}^{\infty }\subset W$
. For this reason, we write
![]() $e^{*}_{i}\in c_{00}$
when referring to
$e^{*}_{i}\in c_{00}$
when referring to
![]() $e_{i}$
as a norming functional. The support of
$e_{i}$
as a norming functional. The support of
![]() $x=(c_{i})\in c_{00}$
is the set
$x=(c_{i})\in c_{00}$
is the set
![]() $\text {supp}(x)=\{i\in \mathbb {N} \mid c_{i}\neq 0\}$
, and we say that vectors
$\text {supp}(x)=\{i\in \mathbb {N} \mid c_{i}\neq 0\}$
, and we say that vectors
![]() $x_{1},\ldots ,x_{n}\in c_{00}$
are successive if
$x_{1},\ldots ,x_{n}\in c_{00}$
are successive if
![]() $\text {supp}(x_{i-1})<\text {supp}(x_{i})$
for
$\text {supp}(x_{i-1})<\text {supp}(x_{i})$
for
![]() $2\leq i\leq n$
. In this case, we use the shorthand notation
$2\leq i\leq n$
. In this case, we use the shorthand notation
![]() $x_{1}<\ldots <x_{n}$
, and we also write
$x_{1}<\ldots <x_{n}$
, and we also write
![]() $n\leq x$
if
$n\leq x$
if
![]() $n\leq \min \text {supp}(x)$
. A finite or infinite sequence of successive vectors in
$n\leq \min \text {supp}(x)$
. A finite or infinite sequence of successive vectors in
![]() $c_{00}$
is said to be a block sequence of
$c_{00}$
is said to be a block sequence of
![]() $(e_{i})$
.
$(e_{i})$
.
The Schreier sets are an increasing sequence of sets of finite subsets of
![]() $\mathbb {N}$
. These sets are defined inductively as follows:
$\mathbb {N}$
. These sets are defined inductively as follows:
and we write that
once
![]() $S_{n}$
has been defined. We also define the set
$S_{n}$
has been defined. We also define the set
![]() $\mathcal {A}_{3}=\{ F\subset \mathbb {N} \mid \text {card}(F)\leq 3\}$
, and we will be interested in sets of the form
$\mathcal {A}_{3}=\{ F\subset \mathbb {N} \mid \text {card}(F)\leq 3\}$
, and we will be interested in sets of the form
It is easy to see that
![]() $F\in S_{n}\ast \mathcal {A}_{3}$
is the union of at most three sets in
$F\in S_{n}\ast \mathcal {A}_{3}$
is the union of at most three sets in
![]() $S_{n}$
. A block sequence
$S_{n}$
. A block sequence
![]() $x_{1}<\ldots <x_{k}\in c_{00}$
is said to be
$x_{1}<\ldots <x_{k}\in c_{00}$
is said to be
![]() $S_{n}$
-admissible (resp.
$S_{n}$
-admissible (resp.
![]() $S_{n}\ast \mathcal {A}_{3}$
-admissible) if
$S_{n}\ast \mathcal {A}_{3}$
-admissible) if
![]() $\{\min \text {supp}(x_{i})\}_{i=1}^{k}\in S_{n}$
(resp.
$\{\min \text {supp}(x_{i})\}_{i=1}^{k}\in S_{n}$
(resp.
![]() $\{\min \text {supp}(x_{i})\}_{i=1}^{k}\in S_{n}\ast \mathcal {A}_{3}$
).
$\{\min \text {supp}(x_{i})\}_{i=1}^{k}\in S_{n}\ast \mathcal {A}_{3}$
).
Let
![]() $n\in \mathbb {N}$
and let
$n\in \mathbb {N}$
and let
![]() $\varepsilon>0$
. Then, the vector
$\varepsilon>0$
. Then, the vector
![]() $x=\sum _{i\in F}c_{i}e_{i}\in c_{00}$
is said to be an
$x=\sum _{i\in F}c_{i}e_{i}\in c_{00}$
is said to be an
![]() $(n,\varepsilon )$
-basic special convex combination (
$(n,\varepsilon )$
-basic special convex combination (
![]() $(n,\varepsilon )$
-basic scc) if
$(n,\varepsilon )$
-basic scc) if
-
(1)
 $F\in S_{n}$
,
$F\in S_{n}$
,
 $c_{i}\geq 0$
for each
$c_{i}\geq 0$
for each
 $i\in F$
, and
$i\in F$
, and
 $\sum _{i\in F}c_{i}=1$
,
$\sum _{i\in F}c_{i}=1$
, -
(2) For every
 $G\subset F$
with
$G\subset F$
with
 $G\in S_{n-1}$
, we have that
$G\in S_{n-1}$
, we have that
 $\sum _{i\in G}c_{i}<\varepsilon $
,
$\sum _{i\in G}c_{i}<\varepsilon $
,
and we refer the reader to [Reference Argyros and Deliyanni1], [Reference Argyros, Godefroy and Rosenthal3], or [Reference Argyros and Tolias6] for more information. In particular, note that
![]() $\sum _{i\in G}c_{i}<3\varepsilon $
if
$\sum _{i\in G}c_{i}<3\varepsilon $
if
![]() $G\subset F$
with
$G\subset F$
with
![]() $G\in S_{k}\ast \mathcal {A}_{3}$
for
$G\in S_{k}\ast \mathcal {A}_{3}$
for
![]() $k<n$
, and there is also the following useful result which is Proposition 2.3 of [Reference Argyros and Tolias6].
$k<n$
, and there is also the following useful result which is Proposition 2.3 of [Reference Argyros and Tolias6].
Proposition 2.1 Let
![]() $n\in \mathbb {N}$
. Then, for every infinite subset
$n\in \mathbb {N}$
. Then, for every infinite subset
![]() $M\subset \mathbb {N}$
and for every
$M\subset \mathbb {N}$
and for every
![]() $F\subset M$
such that
$F\subset M$
such that
![]() $F\in S_{n}$
is maximal with respect to inclusion, there exist real numbers
$F\in S_{n}$
is maximal with respect to inclusion, there exist real numbers
![]() $(c_{i})_{i\in F}$
so that the vector
$(c_{i})_{i\in F}$
so that the vector
![]() $x=\sum _{i\in F}c_{i}e_{i}\in c_{00}$
is an
$x=\sum _{i\in F}c_{i}e_{i}\in c_{00}$
is an
![]() $(n,3/\min (F))$
-basic scc.
$(n,3/\min (F))$
-basic scc.
Similarly, if
![]() $x_{1}<\ldots <x_{d}\in c_{00}$
and if
$x_{1}<\ldots <x_{d}\in c_{00}$
and if
![]() $s_{i}=\min \text {supp}(x_{i})$
for each
$s_{i}=\min \text {supp}(x_{i})$
for each
![]() $1\leq i\leq d$
, then the vector
$1\leq i\leq d$
, then the vector
![]() $x=\sum _{i=1}^{d}c_{i}x_{i}$
is said to be an
$x=\sum _{i=1}^{d}c_{i}x_{i}$
is said to be an
![]() $(n,\varepsilon )$
-special convex combination (
$(n,\varepsilon )$
-special convex combination (
![]() $(n,\varepsilon )$
-scc) if
$(n,\varepsilon )$
-scc) if
![]() $\sum _{i=1}^{d}c_{i}e_{s_{i}}$
is an
$\sum _{i=1}^{d}c_{i}e_{s_{i}}$
is an
![]() $(n,\varepsilon )$
-basic scc. It follows in this case that
$(n,\varepsilon )$
-basic scc. It follows in this case that
![]() $\sum _{i=1}^{d}c_{i}e_{t_{i}}$
is an
$\sum _{i=1}^{d}c_{i}e_{t_{i}}$
is an
![]() $(n,2\varepsilon )$
-basic scc as well where
$(n,2\varepsilon )$
-basic scc as well where
![]() $t_{i}=\max \text {supp}(x_{i})$
for each
$t_{i}=\max \text {supp}(x_{i})$
for each
![]() $1\leq i\leq d$
because
$1\leq i\leq d$
because
if
![]() $G\subset \{t_{i}\}_{i=1}^{d}$
is
$G\subset \{t_{i}\}_{i=1}^{d}$
is
![]() $S_{n-1}$
-admissible and is therefore a translation to the right of at most two sets
$S_{n-1}$
-admissible and is therefore a translation to the right of at most two sets
![]() $G_{1},G_{2}\subset \{s_{i}\}_{i=1}^{d}$
with
$G_{1},G_{2}\subset \{s_{i}\}_{i=1}^{d}$
with
![]() $G_{1},G_{2}\in S_{n-1}$
.
$G_{1},G_{2}\in S_{n-1}$
.
Finally, two specific asymptotic structures appear in this paper. The first is that of a spreading model from [Reference Brunel and Sucheston9], recalled in page 2. It is a consequence of Ramsey’s theorem that every normalized basic sequence
![]() $(x_{i})$
in a Banach space X has a subsequence that generates a spreading model of X. We now define the notion of a Haar-
$(x_{i})$
in a Banach space X has a subsequence that generates a spreading model of X. We now define the notion of a Haar-
![]() $\ell _{1}^{+}$
sequence, and we need first the definition of a Haar system of partitions of
$\ell _{1}^{+}$
sequence, and we need first the definition of a Haar system of partitions of
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
Definition 2.1 A collection
![]() $(A^{n}_{j})_{j=0,n\in \mathbb {N}}^{2^{n}-1}$
of infinite subsets of
$(A^{n}_{j})_{j=0,n\in \mathbb {N}}^{2^{n}-1}$
of infinite subsets of
![]() $\mathbb {N}$
is said to be a Haar system of partitions of
$\mathbb {N}$
is said to be a Haar system of partitions of
![]() $\mathbb {N}$
if the following two conditions are satisfied:
$\mathbb {N}$
if the following two conditions are satisfied:
-
(1) For every
 $n\in \mathbb {N}$
, we have that
$n\in \mathbb {N}$
, we have that
 $\cup _{j=0}^{2^{n}-1}A^{n}_{j}=\mathbb {N}$
and
$\cup _{j=0}^{2^{n}-1}A^{n}_{j}=\mathbb {N}$
and
 $A^{n}_{j}\cap A^{n}_{j'}=\emptyset $
if
$A^{n}_{j}\cap A^{n}_{j'}=\emptyset $
if
 $j\neq j'$
.
$j\neq j'$
. -
(2) For every
 $n\in \mathbb {N}$
and for every
$n\in \mathbb {N}$
and for every
 $0\leq j\leq 2^{n}-1$
, we have that
$0\leq j\leq 2^{n}-1$
, we have that
 $A^{n}_{j}= A^{n+1}_{2j}\cup A^{n+1}_{2j+1}$
.
$A^{n}_{j}= A^{n+1}_{2j}\cup A^{n+1}_{2j+1}$
.
The connection between the Haar-
![]() $\ell _{1}^{+}$
condition (defined below) and Riemann integrability is due to the fact that the infinite set
$\ell _{1}^{+}$
condition (defined below) and Riemann integrability is due to the fact that the infinite set
![]() $A^{n}_{j}$
of the Haar system of partitions of
$A^{n}_{j}$
of the Haar system of partitions of
![]() $\mathbb {N}$
corresponds to the dyadic rational numbers in the dyadic interval
$\mathbb {N}$
corresponds to the dyadic rational numbers in the dyadic interval
![]() $\left (\frac {j}{2^{n}},\frac {j+1}{2^{n}}\right )$
(see, for example, [Reference Gaebler and Sari11, Theorem 3.1]).
$\left (\frac {j}{2^{n}},\frac {j+1}{2^{n}}\right )$
(see, for example, [Reference Gaebler and Sari11, Theorem 3.1]).
Definition 2.2 A normalized basic sequence
![]() $(x_{i})$
in X is said to be Haar-
$(x_{i})$
in X is said to be Haar-
![]() $\ell _{1}^{+}$
if, for every Haar system of partitions
$\ell _{1}^{+}$
if, for every Haar system of partitions
![]() $(A^{n}_{j})_{j=0,n\in \mathbb {N}}^{2^{n}-1}$
of
$(A^{n}_{j})_{j=0,n\in \mathbb {N}}^{2^{n}-1}$
of
![]() $\mathbb {N}$
, there exists a constant
$\mathbb {N}$
, there exists a constant
![]() $C>0$
such that
$C>0$
such that
 $$ \begin{align*} C\leq \lim_{n\to\infty}\sup\left\{ \frac{1}{2^{m}}\left\Vert \sum_{j=0}^{2^{m}-1}x_{i_{j}}\right\Vert \;\middle\vert\; m\geq n \text{ and } 2^{m}\leq i_{j}\in A^{m}_{j}\right\}.\end{align*} $$
$$ \begin{align*} C\leq \lim_{n\to\infty}\sup\left\{ \frac{1}{2^{m}}\left\Vert \sum_{j=0}^{2^{m}-1}x_{i_{j}}\right\Vert \;\middle\vert\; m\geq n \text{ and } 2^{m}\leq i_{j}\in A^{m}_{j}\right\}.\end{align*} $$
Remark 2.2 For a Banach space X, the following are equivalent.
-
(1) X has the Lebesgue property.
-
(2) Every normalized basic sequence in X is Haar-
 $\ell _{1}^{+}$
.
$\ell _{1}^{+}$
. -
(3) For every collection
 $(x_\lambda )_{\lambda \in \mathcal {D}}$
of norm-one vectors in X, there exists a constant
$(x_\lambda )_{\lambda \in \mathcal {D}}$
of norm-one vectors in X, there exists a constant
 $\theta>0$
such that, for every
$\theta>0$
such that, for every
 $n\in \mathbb {N}$
, there exists a subset
$n\in \mathbb {N}$
, there exists a subset
 $V\subset \{0,1\}^{n}$
such that for some choice of nodes
$V\subset \{0,1\}^{n}$
such that for some choice of nodes $$ \begin{align*}\theta\leq \frac{1}{2^{n}}\left\Vert\sum_{\lambda\in V} x_{\mu_{\lambda}}\right\Vert \end{align*} $$
$$ \begin{align*}\theta\leq \frac{1}{2^{n}}\left\Vert\sum_{\lambda\in V} x_{\mu_{\lambda}}\right\Vert \end{align*} $$
 $(\mu _{\lambda })_{\lambda \in V}$
with
$(\mu _{\lambda })_{\lambda \in V}$
with
 $\mu _{\lambda }\geq \lambda $
.
$\mu _{\lambda }\geq \lambda $
.
Indeed, the assertion
![]() $(1)\iff (2)$
is established in [Reference Gaebler and Sari11]. In addition, it is easy to see that
$(1)\iff (2)$
is established in [Reference Gaebler and Sari11]. In addition, it is easy to see that
![]() $(1)\implies (3)$
as collection witnessing the negation of (3) can be easily used to construct a Dirichlet-type function with Riemann integral zero. Lastly, for
$(1)\implies (3)$
as collection witnessing the negation of (3) can be easily used to construct a Dirichlet-type function with Riemann integral zero. Lastly, for
![]() $(3)\implies (2)$
, if there exists a normalized basic sequence
$(3)\implies (2)$
, if there exists a normalized basic sequence
![]() $(x_i)$
in X that is not Haar-
$(x_i)$
in X that is not Haar-
![]() $\ell _{1}^{+}$
, then it is easy to construct a collection
$\ell _{1}^{+}$
, then it is easy to construct a collection
![]() $(x_{\lambda })_{\lambda \in \mathcal {D}}$
of norm-one vectors for which the claim of
$(x_{\lambda })_{\lambda \in \mathcal {D}}$
of norm-one vectors for which the claim of
![]() $(3)$
does not hold as follows. Fix an order-preserving bijection
$(3)$
does not hold as follows. Fix an order-preserving bijection
![]() $\mathcal {D}\to \{A^n_j\mid n\in \mathbb {N}, 0\leq j\leq 2^n-1\}$
such that, for every
$\mathcal {D}\to \{A^n_j\mid n\in \mathbb {N}, 0\leq j\leq 2^n-1\}$
such that, for every
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $\lambda \mapsto A^{|\lambda |}_{j_\lambda }$
, for some
$\lambda \mapsto A^{|\lambda |}_{j_\lambda }$
, for some
![]() $0\leq j_\lambda \leq 2^{|\lambda |}-1$
. Then, for every
$0\leq j_\lambda \leq 2^{|\lambda |}-1$
. Then, for every
![]() $\lambda \in \mathcal {D}$
, choose
$\lambda \in \mathcal {D}$
, choose
![]() $i_\lambda \in A^{|\lambda |}_{j_\lambda }$
such that
$i_\lambda \in A^{|\lambda |}_{j_\lambda }$
such that
![]() $i_\lambda \geq 2^{|\lambda |}$
and put
$i_\lambda \geq 2^{|\lambda |}$
and put
![]() $x_\lambda = x_{i_\lambda }$
. Note that
$x_\lambda = x_{i_\lambda }$
. Note that
![]() $(x_\lambda )_{\lambda \in \mathcal {D}}$
can be chosen Schauder basic in the lexicographical oder of
$(x_\lambda )_{\lambda \in \mathcal {D}}$
can be chosen Schauder basic in the lexicographical oder of
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
3 Construction of
 $X_{\mathcal {D}}$
and uniformly unique
$X_{\mathcal {D}}$
and uniformly unique
 $\ell _{1}$
spreading model
$\ell _{1}$
spreading model
In this section, we define the norming set W inducing the Banach space
![]() $X_{\mathcal {D}}$
. It is defined as an increasing union
$X_{\mathcal {D}}$
. It is defined as an increasing union
![]() $W = \cup _{k=0}^\infty W_k$
, where
$W = \cup _{k=0}^\infty W_k$
, where
![]() $W_0 = \{\pm e_i^*\}_{i=1}^\infty $
, and, in each step, having defined
$W_0 = \{\pm e_i^*\}_{i=1}^\infty $
, and, in each step, having defined
![]() $W_k$
, we formulate the operations and constraints that are used to produce
$W_k$
, we formulate the operations and constraints that are used to produce
![]() $W_{k+1}$
. The quantification of the metric constraints discussed in the introduction is defined inductively and carries a certain complexity; this is necessary to balance the uniform uniqueness of
$W_{k+1}$
. The quantification of the metric constraints discussed in the introduction is defined inductively and carries a certain complexity; this is necessary to balance the uniform uniqueness of
![]() $\ell _1$
spreading models with the
$\ell _1$
spreading models with the
![]() $\ell _\infty $
estimates on tree-indexed collection. At the end of this section, we prove that every normalized weakly null sequence in
$\ell _\infty $
estimates on tree-indexed collection. At the end of this section, we prove that every normalized weakly null sequence in
![]() $X_{\mathcal {D}}$
has a subsequence generating a spreading model that is 102-equivalent to the unit vector basis of
$X_{\mathcal {D}}$
has a subsequence generating a spreading model that is 102-equivalent to the unit vector basis of
![]() $\ell _1$
.
$\ell _1$
.
Fix a pair of strictly increasing sequences
![]() $(m_{j})$
and
$(m_{j})$
and
![]() $(n_{j})$
of positive integers such that
$(n_{j})$
of positive integers such that
![]() $m_{1}=100$
,
$m_{1}=100$
,
![]() $n_{1}=1$
,
$n_{1}=1$
,
-
(1)
 $m_{j+1}\geq j^2m_j^2$
, for every
$m_{j+1}\geq j^2m_j^2$
, for every
 $j\in \mathbb {N}$
,
$j\in \mathbb {N}$
, -
(2)
 $n_{j+1}>\frac {4}{\log (100)}n_{j}\log (m_{j+1})$
.
$n_{j+1}>\frac {4}{\log (100)}n_{j}\log (m_{j+1})$
.
Let
![]() $\mathcal {D} = \cup _{n=0}^\infty \{0,1\}^n$
with the partial order and metric d defined in the introduction. We note that the completion
$\mathcal {D} = \cup _{n=0}^\infty \{0,1\}^n$
with the partial order and metric d defined in the introduction. We note that the completion
![]() $\overline {\mathcal {D}}$
of
$\overline {\mathcal {D}}$
of
![]() $\mathcal {D}$
is a compact metric space. Denote
$\mathcal {D}$
is a compact metric space. Denote
![]() $\mathcal {M} = \{\infty \}\cup \{m_j:j\in \mathbb {N}\}$
and let
$\mathcal {M} = \{\infty \}\cup \{m_j:j\in \mathbb {N}\}$
and let
![]() $\phi :\mathcal {M}\to \mathcal {D}$
be a bijection so that the nodes of
$\phi :\mathcal {M}\to \mathcal {D}$
be a bijection so that the nodes of
![]() $\mathcal {D}$
are ordered lexicographically with respect to
$\mathcal {D}$
are ordered lexicographically with respect to
![]() $\mathcal {M}$
; that is,
$\mathcal {M}$
; that is,
![]() $\phi (\infty ) = \emptyset $
,
$\phi (\infty ) = \emptyset $
,
![]() $\phi (m_{1}) = (0)$
,
$\phi (m_{1}) = (0)$
,
![]() $\phi (m_{2})=(1)$
,
$\phi (m_{2})=(1)$
,
![]() $\phi (m_{3}) = (0,0)$
, and so on. Lastly, as a matter of notational convenience, we always write
$\phi (m_{3}) = (0,0)$
, and so on. Lastly, as a matter of notational convenience, we always write
![]() $d(m_{j},\cdot )$
instead of the formally correct
$d(m_{j},\cdot )$
instead of the formally correct
![]() $d(\phi (m_{j}),\cdot )$
.
$d(\phi (m_{j}),\cdot )$
.
Now, let
![]() $W_{0}=\{\pm e_{i}^{*}\}_{i=1}^{\infty }\subset c_{00}$
and write
$W_{0}=\{\pm e_{i}^{*}\}_{i=1}^{\infty }\subset c_{00}$
and write
![]() $w(\pm e^{*}_{i})=m(\pm e^{*}_{i})=\infty $
for each
$w(\pm e^{*}_{i})=m(\pm e^{*}_{i})=\infty $
for each
![]() $i\in \mathbb {N}$
. Then, define the set
$i\in \mathbb {N}$
. Then, define the set
 $$ \begin{align*} W_{1}=W_{0}\cup\left\{\frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{k=1}^{d}e^{*}_{i_{k}} \;\middle\vert\; \substack{ e^{*}_{i_{1}}<\ldots<e^{*}_{i_{d}} \text{ are } \\ S_{n_{j_{1}}+\cdots+n_{j_{l}}}\text{-admissible}} \right\}, \end{align*} $$
$$ \begin{align*} W_{1}=W_{0}\cup\left\{\frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{k=1}^{d}e^{*}_{i_{k}} \;\middle\vert\; \substack{ e^{*}_{i_{1}}<\ldots<e^{*}_{i_{d}} \text{ are } \\ S_{n_{j_{1}}+\cdots+n_{j_{l}}}\text{-admissible}} \right\}, \end{align*} $$
where
![]() $w(f)=m_{j_{1}}\cdots m_{j_{l}}$
,
$w(f)=m_{j_{1}}\cdots m_{j_{l}}$
,
![]() $\vec w(f) = (m_{j_1},\ldots ,m_{j_\ell })$
, and
$\vec w(f) = (m_{j_1},\ldots ,m_{j_\ell })$
, and
![]() $m(f)=\max _{1\leq z\leq l}m_{j_{z}}$
for
$m(f)=\max _{1\leq z\leq l}m_{j_{z}}$
for
![]() $f\in W_{1}\setminus W_{0}$
. For f in
$f\in W_{1}\setminus W_{0}$
. For f in
![]() $W_1\setminus W_0$
,
$W_1\setminus W_0$
,
![]() $\vec w(f)$
may not be uniquely defined, and thus neither are
$\vec w(f)$
may not be uniquely defined, and thus neither are
![]() $w(f)$
and
$w(f)$
and
![]() $m(f)$
. The notation
$m(f)$
. The notation
![]() $\vec w(f) = (m_{j_1},\ldots ,m_{j_\ell })$
means that f admits a representation as above, and it is fixed while working with f. This will also apply to
$\vec w(f) = (m_{j_1},\ldots ,m_{j_\ell })$
means that f admits a representation as above, and it is fixed while working with f. This will also apply to
![]() $f\in W_k$
,
$f\in W_k$
,
![]() $k>1$
. This is common in this type of construction and does not pose a problem. In fact, insisting on uniquely defining the weight may interfere with constructing functionals that are used to prove the properties of the space. We next define the following notion of proximity with respect to
$k>1$
. This is common in this type of construction and does not pose a problem. In fact, insisting on uniquely defining the weight may interfere with constructing functionals that are used to prove the properties of the space. We next define the following notion of proximity with respect to
![]() $\overline {\mathcal {D}}$
for functionals in
$\overline {\mathcal {D}}$
for functionals in
![]() $W_{1}$
.
$W_{1}$
.
Definition 3.1 The functionals
![]() $f_{1}<\ldots <f_{d}$
in
$f_{1}<\ldots <f_{d}$
in
![]() $W_{1}$
are said to be
$W_{1}$
are said to be
![]() $(n,\lambda )$
-packed for some
$(n,\lambda )$
-packed for some
![]() $\lambda \in \overline {\mathcal {D}}$
if the following conditions are satisfied:
$\lambda \in \overline {\mathcal {D}}$
if the following conditions are satisfied:
-
(1)
 $f_{1}<\ldots <f_{d}$
are
$f_{1}<\ldots <f_{d}$
are
 $S_{n}$
-admissible,
$S_{n}$
-admissible, -
(2)
 $w(f_{i})\geq 2^{\max \text {supp}(f_{i-1})}$
for
$w(f_{i})\geq 2^{\max \text {supp}(f_{i-1})}$
for
 $2\leq i\leq d$
,
$2\leq i\leq d$
, -
(3)
 $d(m(f_{i}),\lambda )\leq 2^{-\max \text {supp}(f_{i-1})}$
for
$d(m(f_{i}),\lambda )\leq 2^{-\max \text {supp}(f_{i-1})}$
for
 $2\leq i\leq d$
,
$2\leq i\leq d$
,
and if, in addition, we have that
![]() $\max _{1\leq i\leq d}d(m(f_{i}),\lambda )\leq \eta $
. Then
$\max _{1\leq i\leq d}d(m(f_{i}),\lambda )\leq \eta $
. Then
![]() $f_{1}<\ldots <f_{d}$
are said to be
$f_{1}<\ldots <f_{d}$
are said to be
![]() $(n,\lambda ,\eta )$
-packed.
$(n,\lambda ,\eta )$
-packed.
This definition allows for the following inductive definition as well.
Definition 3.2 The functionals
![]() $f_{1}<\ldots <f_{d}$
in
$f_{1}<\ldots <f_{d}$
in
![]() $W_{1}$
are said to be
$W_{1}$
are said to be
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},\lambda )$
-packed for some
$(n_{j_{1}},\ldots ,n_{j_{l}},\lambda )$
-packed for some
![]() $\lambda \in \overline {\mathcal {D}}$
if the following claims hold:
$\lambda \in \overline {\mathcal {D}}$
if the following claims hold:
-
(1)
 $w(f_{i})\geq 2^{\max \text {supp}(f_{i-1})}$
for
$w(f_{i})\geq 2^{\max \text {supp}(f_{i-1})}$
for
 $2\leq i\leq d$
,
$2\leq i\leq d$
, -
(2) There exists a partition
 $F_{1}<\ldots <F_{M}$
of
$F_{1}<\ldots <F_{M}$
of
 $\{1,\ldots ,d\}$
such that the set
$\{1,\ldots ,d\}$
such that the set
 $\{f_{\min (F_{k})}\}_{k=1}^{M}$
is
$\{f_{\min (F_{k})}\}_{k=1}^{M}$
is
 $S_{n_{j_{l}}}$
-admissible,
$S_{n_{j_{l}}}$
-admissible, -
(3) There exist nodes
 $\lambda _{1},\ldots ,\lambda _{M}\in \overline {\mathcal {D}}$
such that
$\lambda _{1},\ldots ,\lambda _{M}\in \overline {\mathcal {D}}$
such that-
(a)
 $(f_{i})_{i\in F_{1}}$
is
$(f_{i})_{i\in F_{1}}$
is
 $(n_{j_{1}},\ldots ,n_{j_{l-1}},\lambda _{1})$
-packed,
$(n_{j_{1}},\ldots ,n_{j_{l-1}},\lambda _{1})$
-packed, -
(b)
 $(f_{i})_{i\in F_{k}}$
is
$(f_{i})_{i\in F_{k}}$
is
 $(n_{j_{1}},\ldots ,n_{j_{l-1}},\lambda _{k},2^{-\max \text {supp}(f_{\max (F_{k-1})})})$
-packed for
$(n_{j_{1}},\ldots ,n_{j_{l-1}},\lambda _{k},2^{-\max \text {supp}(f_{\max (F_{k-1})})})$
-packed for
 $2\leq k\leq M$
,
$2\leq k\leq M$
, -
(c)
 $d(\lambda _{k},\lambda )\leq 2^{-\max \text {supp}(f_{\max (F_{k-1})})}$
for
$d(\lambda _{k},\lambda )\leq 2^{-\max \text {supp}(f_{\max (F_{k-1})})}$
for
 $2\leq k\leq M$
,
$2\leq k\leq M$
,
-
and if, in addition, we have that
![]() $\max _{1\leq i\leq d}d(m(f_{i}),\lambda )\leq \eta $
, then we say that
$\max _{1\leq i\leq d}d(m(f_{i}),\lambda )\leq \eta $
, then we say that
![]() $f_{1}<\ldots <f_{d}$
are
$f_{1}<\ldots <f_{d}$
are
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},\lambda ,\eta )$
-packed.
$(n_{j_{1}},\ldots ,n_{j_{l}},\lambda ,\eta )$
-packed.
We now define the next set of weighted functionals
 $$ \begin{align*} W_{2}=W_{1}\cup\left\{ \frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{i=1}^{d}f_{i} \;\middle\vert\; \substack{ f_{1}<\ldots<f_{d} \text{ are in } W_{1} \text{ and are} \\ (n_{j_{1}},\ldots,n_{j_{l}},\lambda)\text{-packed for some } \lambda\in\overline{\mathcal{D}}} \right\} \end{align*} $$
$$ \begin{align*} W_{2}=W_{1}\cup\left\{ \frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{i=1}^{d}f_{i} \;\middle\vert\; \substack{ f_{1}<\ldots<f_{d} \text{ are in } W_{1} \text{ and are} \\ (n_{j_{1}},\ldots,n_{j_{l}},\lambda)\text{-packed for some } \lambda\in\overline{\mathcal{D}}} \right\} \end{align*} $$
with
![]() $w(f)=m_{j_{1}}\cdots m_{j_{l}}$
,
$w(f)=m_{j_{1}}\cdots m_{j_{l}}$
,
![]() $\vec w(f) = (m_{j_1},\ldots , m_{j_\ell })$
, and
$\vec w(f) = (m_{j_1},\ldots , m_{j_\ell })$
, and
![]() $m(f)=\max _{1\leq z\leq l}m_{j_{z}}$
. Now, once we have defined the sets
$m(f)=\max _{1\leq z\leq l}m_{j_{z}}$
. Now, once we have defined the sets
![]() $W_{0},W_{1},\ldots ,W_{k}$
, we replace
$W_{0},W_{1},\ldots ,W_{k}$
, we replace
![]() $W_{1}$
in Definitions 3.1 and 3.2 with
$W_{1}$
in Definitions 3.1 and 3.2 with
![]() $W_{k}$
, and we write that
$W_{k}$
, and we write that
 $$ \begin{align*} W_{k+1}=W_{k}\cup\left\{ \frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{i=1}^{d}f_{i} \;\middle\vert\; \substack{ f_{1}<\ldots<f_{d} \text{ are in } W_{k} \text{ and are} \\ (n_{j_{1}},\ldots,n_{j_{l}},\lambda)\text{-packed for some } \lambda\in\overline{\mathcal{D}}} \right\} \end{align*} $$
$$ \begin{align*} W_{k+1}=W_{k}\cup\left\{ \frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{i=1}^{d}f_{i} \;\middle\vert\; \substack{ f_{1}<\ldots<f_{d} \text{ are in } W_{k} \text{ and are} \\ (n_{j_{1}},\ldots,n_{j_{l}},\lambda)\text{-packed for some } \lambda\in\overline{\mathcal{D}}} \right\} \end{align*} $$
for each
![]() $k\in \mathbb {N}$
. We then define our norming set
$k\in \mathbb {N}$
. We then define our norming set
![]() $W=\cup _{k=0}^{\infty }W_{k}$
, and we let the Banach space
$W=\cup _{k=0}^{\infty }W_{k}$
, and we let the Banach space
![]() $X_{\mathcal {D}}$
be the completion of
$X_{\mathcal {D}}$
be the completion of
![]() $c_{00}$
with respect to the norm that is given by
$c_{00}$
with respect to the norm that is given by
![]() $\|x\|=\sup \{f(x) \mid f\in W\}$
for
$\|x\|=\sup \{f(x) \mid f\in W\}$
for
![]() $x\in c_{00}$
.
$x\in c_{00}$
.
Remark 3.1 By induction on k, where
![]() $W = \cup _{k=0}^\infty W_k$
, it is easy to prove the following.
$W = \cup _{k=0}^\infty W_k$
, it is easy to prove the following.
-
(1) For every
 $(n_{j_1},\ldots ,n_{j_\ell },\lambda )$
-packed sequence
$(n_{j_1},\ldots ,n_{j_\ell },\lambda )$
-packed sequence
 $f_1<\cdots <f_d$
in W, is in W.
$f_1<\cdots <f_d$
in W, is in W. $$\begin{align*}f = \frac{1}{m_{j_1}\cdots m_{j_\ell}}\sum_{i=1}^df_i\end{align*}$$
$$\begin{align*}f = \frac{1}{m_{j_1}\cdots m_{j_\ell}}\sum_{i=1}^df_i\end{align*}$$
Incorporating a nested induction on
![]() $\ell $
, the following items can be shown.
$\ell $
, the following items can be shown.
-
(2) A subsequence of a
 $(n_{j_1},\ldots ,n_{j_\ell },\lambda )$
-packed sequence
$(n_{j_1},\ldots ,n_{j_\ell },\lambda )$
-packed sequence
 $f_1<\cdots <f_d$
in W is also
$f_1<\cdots <f_d$
in W is also
 $(n_{j_1},\ldots ,n_{j_\ell },\lambda )$
-packed.
$(n_{j_1},\ldots ,n_{j_\ell },\lambda )$
-packed. -
(3) If
 $f_1<\cdots <f_d$
is a
$f_1<\cdots <f_d$
is a
 $(n_{j_1},\ldots ,n_{j_\ell },\lambda )$
-packed sequence in W and
$(n_{j_1},\ldots ,n_{j_\ell },\lambda )$
-packed sequence in W and
 $g_1<\cdots <g_d$
are in
$g_1<\cdots <g_d$
are in
 $c_{00}$
such that, for
$c_{00}$
such that, for
 $1\leq i\leq d$
and
$1\leq i\leq d$
and
 $s\in \mathrm {supp}(g_i)$
, we have
$s\in \mathrm {supp}(g_i)$
, we have
 $|g_i(e_s)| = |f_i(e_s)|$
, then
$|g_i(e_s)| = |f_i(e_s)|$
, then
 $g_1$
,…,
$g_1$
,…,
 $g_d$
are also in W, and they are
$g_d$
are also in W, and they are
 $(n_{j_1},\ldots ,n_{j_\ell },\lambda )$
-packed.
$(n_{j_1},\ldots ,n_{j_\ell },\lambda )$
-packed.
In particular, (2) and (3) yield that W is closed under restricting the supports of its members to subsets and changing the signs of their scalar coefficients, and thus,
![]() $(e_i)$
is a 1-unconditional basis for
$(e_i)$
is a 1-unconditional basis for
![]() $X_{\mathcal {D}}$
.
$X_{\mathcal {D}}$
.
We now prove that every spreading model of
![]() $X_{\mathcal {D}}$
is uniformly equivalent to the unit vector basis of
$X_{\mathcal {D}}$
is uniformly equivalent to the unit vector basis of
![]() $\ell _{1}$
. In fact, the precise statement of the following theorem is slightly stronger than this assertion; it will be required in its full generality later, in the proof of Proposition 5.2.
$\ell _{1}$
. In fact, the precise statement of the following theorem is slightly stronger than this assertion; it will be required in its full generality later, in the proof of Proposition 5.2.
Theorem 3.2 Let
![]() $(x_{r})$
be a normalized block sequence of
$(x_{r})$
be a normalized block sequence of
![]() $(e_{i})$
. Then, there exists an infinite subset
$(e_{i})$
. Then, there exists an infinite subset
![]() $\Omega \subset \mathbb {N}$
such that, for every
$\Omega \subset \mathbb {N}$
such that, for every
![]() $j_{0}\in \mathbb {N}$
, there is the estimate
$j_{0}\in \mathbb {N}$
, there is the estimate
 $$ \begin{align*} \left\Vert \sum_{r\in F}c_{r}x_{r}\right\Vert \geq 0.99\frac{1}{m_{j_{0}}}\sum_{r\in \Gamma}|c_{r}| \end{align*} $$
$$ \begin{align*} \left\Vert \sum_{r\in F}c_{r}x_{r}\right\Vert \geq 0.99\frac{1}{m_{j_{0}}}\sum_{r\in \Gamma}|c_{r}| \end{align*} $$
for every subset
![]() $\Gamma \subset \Omega $
such that
$\Gamma \subset \Omega $
such that
![]() $(x_{r})_{r\in \Gamma }$
are
$(x_{r})_{r\in \Gamma }$
are
![]() $S_{n_{j_{0}}}$
-admissible and for every choice
$S_{n_{j_{0}}}$
-admissible and for every choice
![]() $(c_{r})_{r\in \Gamma }$
of scalars.
$(c_{r})_{r\in \Gamma }$
of scalars.
Proof Choose for every
![]() $r\in \mathbb {N}$
a norming functional
$r\in \mathbb {N}$
a norming functional
![]() $f_{r}\in W$
so that
$f_{r}\in W$
so that
![]() $f_{r}(x_{r})=1$
and so that
$f_{r}(x_{r})=1$
and so that
![]() $\text {supp}(f_{r})\subset \text {supp}(x_{r})$
. Then, there are two cases to consider.
$\text {supp}(f_{r})\subset \text {supp}(x_{r})$
. Then, there are two cases to consider.
-
(i)
 $\limsup _{r\to \infty }w(f_{r})=L<\infty $
$\limsup _{r\to \infty }w(f_{r})=L<\infty $
Here, we may pass to an infinite subset
![]() $\Omega _{1}\subset \mathbb {N}$
so that
$\Omega _{1}\subset \mathbb {N}$
so that
![]() $w(f_{r})=m_{j_{1}}\cdots m_{j_{l}}$
for each
$w(f_{r})=m_{j_{1}}\cdots m_{j_{l}}$
for each
![]() $r\in \Omega _{1}$
. Note that each
$r\in \Omega _{1}$
. Note that each
![]() $f_{r}$
with
$f_{r}$
with
![]() $r\in \Omega _{1}$
is then
$r\in \Omega _{1}$
is then
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},\lambda _{r})$
-packed for some
$(n_{j_{1}},\ldots ,n_{j_{l}},\lambda _{r})$
-packed for some
![]() $\lambda _{r}\in \overline {\mathcal {D}}$
. We may then pass to a further infinite subset
$\lambda _{r}\in \overline {\mathcal {D}}$
. We may then pass to a further infinite subset
![]() $\Omega _{2}\subset \Omega _{1}$
so that
$\Omega _{2}\subset \Omega _{1}$
so that
![]() $d(\lambda _{r},\lambda )\leq \frac {1}{2}\cdot 2^{-\max \text {supp}(x_{r-1})}$
for each
$d(\lambda _{r},\lambda )\leq \frac {1}{2}\cdot 2^{-\max \text {supp}(x_{r-1})}$
for each
![]() $r\in \Omega _{2}\setminus \{\min (\Omega _{2})\}$
and for some
$r\in \Omega _{2}\setminus \{\min (\Omega _{2})\}$
and for some
![]() $\lambda \in \overline {\mathcal {D}}$
. Now, let
$\lambda \in \overline {\mathcal {D}}$
. Now, let
![]() $\Omega =\Omega _{2}$
and consider the subsequence
$\Omega =\Omega _{2}$
and consider the subsequence
![]() $(x_{r})_{r\in \Omega _{2}}$
. Let
$(x_{r})_{r\in \Omega _{2}}$
. Let
![]() $\Gamma \subset \Omega $
be a subset such that the block vectors
$\Gamma \subset \Omega $
be a subset such that the block vectors
![]() $(x_{r})_{r\in \Gamma }$
are
$(x_{r})_{r\in \Gamma }$
are
![]() $S_{n_{j_{0}}}$
-admissible and let
$S_{n_{j_{0}}}$
-admissible and let
 $$ \begin{align*} f_{r}=\frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{q=1}^{d_{r}}f^{r}_{q} \qquad r\in\Gamma \end{align*} $$
$$ \begin{align*} f_{r}=\frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{q=1}^{d_{r}}f^{r}_{q} \qquad r\in\Gamma \end{align*} $$
be the associated norming functionals. For each
![]() $r\in \Gamma $
, let
$r\in \Gamma $
, let
![]() $F^{r}_{1}<\ldots <F^{r}_{M_{r}}$
be the partition of
$F^{r}_{1}<\ldots <F^{r}_{M_{r}}$
be the partition of
![]() $\{1,\ldots ,d_{r}\}$
and let
$\{1,\ldots ,d_{r}\}$
and let
![]() $\lambda ^{r}_{1},\ldots ,\lambda ^{r}_{M_{r}}\in \overline {\mathcal {D}}$
be the corresponding nodes so that Definition 3.2 is satisfied because the functionals
$\lambda ^{r}_{1},\ldots ,\lambda ^{r}_{M_{r}}\in \overline {\mathcal {D}}$
be the corresponding nodes so that Definition 3.2 is satisfied because the functionals
![]() $f^{r}_{1}<\ldots <f^{r}_{d_{r}}$
are
$f^{r}_{1}<\ldots <f^{r}_{d_{r}}$
are
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},\lambda _{r})$
-packed. We will now show that the concatenation
$(n_{j_{1}},\ldots ,n_{j_{l}},\lambda _{r})$
-packed. We will now show that the concatenation
is in W. First, note that there is some
![]() $\kappa \in \mathbb {N}$
so that each functional in this concatenation is a member of
$\kappa \in \mathbb {N}$
so that each functional in this concatenation is a member of
![]() $W_{\kappa }$
. It therefore remains to show that these functionals are
$W_{\kappa }$
. It therefore remains to show that these functionals are
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},n_{j_{0}},\lambda )$
-packed. Indeed, it follows immediately that they are
$(n_{j_{1}},\ldots ,n_{j_{l}},n_{j_{0}},\lambda )$
-packed. Indeed, it follows immediately that they are
![]() $S_{n_{j_{1}}+\cdots +n_{j_{l}}+n_{j_{0}}}$
-admissible and are very fast-growing in the sense of Definition 3.2. Then, let
$S_{n_{j_{1}}+\cdots +n_{j_{l}}+n_{j_{0}}}$
-admissible and are very fast-growing in the sense of Definition 3.2. Then, let
![]() $F_{\min (\Gamma )}<\ldots <F_{\max (\Gamma )}$
be the partition of the number of functionals in the above concatenation such that
$F_{\min (\Gamma )}<\ldots <F_{\max (\Gamma )}$
be the partition of the number of functionals in the above concatenation such that
![]() $(f_{i})_{i\in F_{r}}=\{f^{r}_{\min (F^{r}_{2})},\ldots ,f^{r}_{d_{r}}\}$
and note that
$(f_{i})_{i\in F_{r}}=\{f^{r}_{\min (F^{r}_{2})},\ldots ,f^{r}_{d_{r}}\}$
and note that
![]() $\{f_{\min (F_{r})}\}_{r\in \Gamma }=\{f^{r}_{\min (F^{r}_{2})}\}_{r\in \Gamma }$
is
$\{f_{\min (F_{r})}\}_{r\in \Gamma }=\{f^{r}_{\min (F^{r}_{2})}\}_{r\in \Gamma }$
is
![]() $S_{n_{j_{0}}}$
-admissible. Moreover,
$S_{n_{j_{0}}}$
-admissible. Moreover,
-
(1)
 $(f_{i})_{i\in F_{1}}=\{f^{1}_{\min (F^{1}_{2})},\ldots ,f^{1}_{d_{1}}\}$
is
$(f_{i})_{i\in F_{1}}=\{f^{1}_{\min (F^{1}_{2})},\ldots ,f^{1}_{d_{1}}\}$
is
 $(n_{j_{1}},\ldots ,n_{j_{l}},\lambda _{1})$
-packed.
$(n_{j_{1}},\ldots ,n_{j_{l}},\lambda _{1})$
-packed. -
(2)
 $(f_{i})_{i\in F_{r}}=\{f^{r}_{\min (F^{r}_{2})},\ldots ,f^{r}_{d_{r}}\}$
is
$(f_{i})_{i\in F_{r}}=\{f^{r}_{\min (F^{r}_{2})},\ldots ,f^{r}_{d_{r}}\}$
is
 $(n_{j_{1}},\ldots ,n_{j_{l}},\lambda _{r})$
-packed for each
$(n_{j_{1}},\ldots ,n_{j_{l}},\lambda _{r})$
-packed for each
 $r\in \Gamma \setminus \{\min (\Gamma )\}$
and, in addition, for each
$r\in \Gamma \setminus \{\min (\Gamma )\}$
and, in addition, for each
 $f_{i}$
with
$f_{i}$
with
 $i\in F^{r}_{k}$
(where
$i\in F^{r}_{k}$
(where
 $2\leq k\leq M_{r}$
), there is so that, in fact,
$2\leq k\leq M_{r}$
), there is so that, in fact, $$ \begin{align*} d(m(f_{i}),\lambda_{r}) &\leq d(m(f_{i}),\lambda^{r}_{k})+d(\lambda^{r}_{k},\lambda_{r}) \\ &\leq 2\cdot 2^{-\max\text{supp}(f_{\max(F^{r}_{k-1})})}\leq 2^{-\max\text{supp}(f_{\max(F_{r-1})})}\end{align*} $$
$$ \begin{align*} d(m(f_{i}),\lambda_{r}) &\leq d(m(f_{i}),\lambda^{r}_{k})+d(\lambda^{r}_{k},\lambda_{r}) \\ &\leq 2\cdot 2^{-\max\text{supp}(f_{\max(F^{r}_{k-1})})}\leq 2^{-\max\text{supp}(f_{\max(F_{r-1})})}\end{align*} $$
 $(f_{i})_{i\in F_{r}}$
is
$(f_{i})_{i\in F_{r}}$
is
 $(n_{j_{1}},\ldots ,n_{j_{l}},\lambda _{r}, 2^{-\max \text {supp}(f_{\max (F_{r-1})})})$
-packed.
$(n_{j_{1}},\ldots ,n_{j_{l}},\lambda _{r}, 2^{-\max \text {supp}(f_{\max (F_{r-1})})})$
-packed.
-
(3)
 $d(\lambda _{r},\lambda )\leq \frac {1}{2}\cdot 2^{-\max \text {supp}(x_{r-1})}\leq 2^{-\max \text {supp}(f_{\max (F_{r-1})})}$
for each
$d(\lambda _{r},\lambda )\leq \frac {1}{2}\cdot 2^{-\max \text {supp}(x_{r-1})}\leq 2^{-\max \text {supp}(f_{\max (F_{r-1})})}$
for each
 $r\in \Gamma \setminus \{\min (\Gamma )\}$
.
$r\in \Gamma \setminus \{\min (\Gamma )\}$
.
Putting these pieces together, it follows that the functional
 $$ \begin{align*} \mathscr{F}=\frac{1}{m_{j_{1}}\cdots m_{j_{l}}m_{j_{0}}}\sum_{r\in\Gamma}\sum_{q=\min(F^{r}_{2})}^{d_{r}}f^{r}_{q} \end{align*} $$
$$ \begin{align*} \mathscr{F}=\frac{1}{m_{j_{1}}\cdots m_{j_{l}}m_{j_{0}}}\sum_{r\in\Gamma}\sum_{q=\min(F^{r}_{2})}^{d_{r}}f^{r}_{q} \end{align*} $$
is
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},n_{j_{0}},\lambda )$
-packed and is therefore a member of
$(n_{j_{1}},\ldots ,n_{j_{l}},n_{j_{0}},\lambda )$
-packed and is therefore a member of
![]() $W_{\kappa +1}\subset W$
. Now, because
$W_{\kappa +1}\subset W$
. Now, because
![]() $(x_{r})_{r\in \Omega }$
is itself
$(x_{r})_{r\in \Omega }$
is itself
![]() $1$
-unconditional, there is the estimate
$1$
-unconditional, there is the estimate
 $$ \begin{align*} \left\Vert \sum_{r\in \Gamma}c_{r}x_{r}\right\Vert = \left\Vert \sum_{r\in\Gamma}|c_{r}|x_{r}\right\Vert &\geq\mathscr{F}\left(\sum_{r\in\Gamma}|c_{r}|x_{r}\right) \\ &=\frac{1}{m_{j_{1}}\cdots m_{j_{l}}m_{j_{0}}}\sum_{r\in\Gamma}\sum_{q=\min(F^{r}_{2})}^{d_{r}}f^{r}_{q}\left(\sum_{p\in\Gamma}|c_{p}|x_{p}\right) \\ &=\frac{1}{m_{j_{0}}}\sum_{r\in\Gamma}\frac{|c_{r}|}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{q=\min(F^{r}_{2})}^{d_{r}}f^{r}_{q}(x_{r}) \\ &=\frac{1}{m_{j_{0}}}\sum_{r\in\Gamma}|c_{r}|\left(f_{r}(x_{r})-\frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{q\in F^{r}_{1}}f^{r}_{q}(x_{r})\right) \\ &\geq \frac{1}{m_{j_{0}}}\sum_{r\in\Gamma}|c_{r}|\left(1 - \frac{1}{m_{j_{l}}}\cdot\frac{1}{m_{j_{1}}\cdots m_{j_{l-1}}}\sum_{q\in F^{r}_{1}}f^{r}_{q}(x_{r})\right) \\ &\geq \frac{1}{m_{j_{0}}}\sum_{r\in\Gamma}|c_{r}|\left(1-\frac{1}{m_{1}}\right) = \frac{m_{1}-1}{m_{1}m_{j_{0}}}\sum_{r\in\Gamma}|c_{r}|,\end{align*} $$
$$ \begin{align*} \left\Vert \sum_{r\in \Gamma}c_{r}x_{r}\right\Vert = \left\Vert \sum_{r\in\Gamma}|c_{r}|x_{r}\right\Vert &\geq\mathscr{F}\left(\sum_{r\in\Gamma}|c_{r}|x_{r}\right) \\ &=\frac{1}{m_{j_{1}}\cdots m_{j_{l}}m_{j_{0}}}\sum_{r\in\Gamma}\sum_{q=\min(F^{r}_{2})}^{d_{r}}f^{r}_{q}\left(\sum_{p\in\Gamma}|c_{p}|x_{p}\right) \\ &=\frac{1}{m_{j_{0}}}\sum_{r\in\Gamma}\frac{|c_{r}|}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{q=\min(F^{r}_{2})}^{d_{r}}f^{r}_{q}(x_{r}) \\ &=\frac{1}{m_{j_{0}}}\sum_{r\in\Gamma}|c_{r}|\left(f_{r}(x_{r})-\frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{q\in F^{r}_{1}}f^{r}_{q}(x_{r})\right) \\ &\geq \frac{1}{m_{j_{0}}}\sum_{r\in\Gamma}|c_{r}|\left(1 - \frac{1}{m_{j_{l}}}\cdot\frac{1}{m_{j_{1}}\cdots m_{j_{l-1}}}\sum_{q\in F^{r}_{1}}f^{r}_{q}(x_{r})\right) \\ &\geq \frac{1}{m_{j_{0}}}\sum_{r\in\Gamma}|c_{r}|\left(1-\frac{1}{m_{1}}\right) = \frac{m_{1}-1}{m_{1}m_{j_{0}}}\sum_{r\in\Gamma}|c_{r}|,\end{align*} $$
where we have used the fact that
![]() $\frac {1}{m_{j_{1}}\cdots m_{j_{l-1}}}\sum _{q\in F^{r}_{1}}f^{r}_{q}\in W$
, and this completes the proof for the first case.
$\frac {1}{m_{j_{1}}\cdots m_{j_{l-1}}}\sum _{q\in F^{r}_{1}}f^{r}_{q}\in W$
, and this completes the proof for the first case.
-
(ii)
 $\limsup _{r\to \infty }w(f_{r})=\infty $
$\limsup _{r\to \infty }w(f_{r})=\infty $
In this case, there exists an infinite subset
![]() $\Omega _{1}\subset \mathbb {N}$
such that
$\Omega _{1}\subset \mathbb {N}$
such that
![]() $w(f_{r})$
for
$w(f_{r})$
for
![]() $r\in \Omega _{1}\setminus \{\min (\Omega _{1})\}$
is very fast-growing in the sense of Definition 3.1. Then, let
$r\in \Omega _{1}\setminus \{\min (\Omega _{1})\}$
is very fast-growing in the sense of Definition 3.1. Then, let
![]() $\lambda _{r}$
be the node in
$\lambda _{r}$
be the node in
![]() $\overline {\mathcal {D}}$
that corresponds to
$\overline {\mathcal {D}}$
that corresponds to
![]() $m(f_{r})$
for each
$m(f_{r})$
for each
![]() $r\in \Omega _{1}$
. We may then pass to a further infinite subset
$r\in \Omega _{1}$
. We may then pass to a further infinite subset
![]() $\Omega _{2}\subset \Omega _{1}$
so that
$\Omega _{2}\subset \Omega _{1}$
so that
![]() $d(\lambda _{r},\lambda )\leq \frac {1}{2}\cdot 2^{-\max \text {supp}(x_{r-1})}$
for some
$d(\lambda _{r},\lambda )\leq \frac {1}{2}\cdot 2^{-\max \text {supp}(x_{r-1})}$
for some
![]() $\lambda \in \overline {\mathcal {D}}$
and for each
$\lambda \in \overline {\mathcal {D}}$
and for each
![]() $r\in \Omega _{2}\setminus \{\min (\Omega _{2})\}$
. Now, let
$r\in \Omega _{2}\setminus \{\min (\Omega _{2})\}$
. Now, let
![]() $\Omega =\Omega _{2}$
and consider the subsequence
$\Omega =\Omega _{2}$
and consider the subsequence
![]() $(x_{r})_{r\in \Omega }$
. Let
$(x_{r})_{r\in \Omega }$
. Let
![]() $\Gamma \subset \Omega $
be a subset such that the block vectors
$\Gamma \subset \Omega $
be a subset such that the block vectors
![]() $(x_{r})_{r\in \Gamma }$
are
$(x_{r})_{r\in \Gamma }$
are
![]() $S_{n_{j_{0}}}$
-admissible and let
$S_{n_{j_{0}}}$
-admissible and let
![]() $f_{\min (\Gamma )}<\ldots <f_{\max (\Gamma )}$
be the corresponding norming functionals. Note that there is some
$f_{\min (\Gamma )}<\ldots <f_{\max (\Gamma )}$
be the corresponding norming functionals. Note that there is some
![]() $\kappa \in \mathbb {N}$
so that
$\kappa \in \mathbb {N}$
so that
![]() $f_{r}\in W_{\kappa }$
for each
$f_{r}\in W_{\kappa }$
for each
![]() $r\in \Gamma $
. Note also that, by construction, these norming functionals are
$r\in \Gamma $
. Note also that, by construction, these norming functionals are
![]() $S_{n_{j_{0}}}$
-admissible and are very fast-growing in the sense of Definition 3.1. Moreover, there is the estimate
$S_{n_{j_{0}}}$
-admissible and are very fast-growing in the sense of Definition 3.1. Moreover, there is the estimate
for each
![]() $r\in \Gamma \setminus \{\min (\Gamma )\}$
so that these functionals are
$r\in \Gamma \setminus \{\min (\Gamma )\}$
so that these functionals are
![]() $(n_{j_{0}},\lambda )$
-packed. Then, we have that
$(n_{j_{0}},\lambda )$
-packed. Then, we have that
![]() $\frac {1}{m_{j_{0}}}\sum _{r\in \Gamma }f_{r}\in W_{\kappa +1}\subset W$
so that
$\frac {1}{m_{j_{0}}}\sum _{r\in \Gamma }f_{r}\in W_{\kappa +1}\subset W$
so that
 $$ \begin{align*} \left\Vert \sum_{r\in\Gamma}c_{r}x_{r}\right\Vert =\left\Vert \sum_{r\in\Gamma}|c_{r}|x_{r}\right\Vert &\geq \frac{1}{m_{j_{0}}}\sum_{r\in\Gamma}f_{r}\left(\sum_{p\in\Gamma}|c_{p}|x_{p}\right) \\ &=\frac{1}{m_{j_{0}}}\sum_{r\in\Gamma}|c_{r}|f_{r}(x_{r})=\frac{1}{m_{j_{0}}}\sum_{r\in\Gamma}|c_{r}|\geq\frac{m_{1}-1}{m_{1}m_{j_{0}}}\sum_{r\in\Gamma}|c_{r}|, \end{align*} $$
$$ \begin{align*} \left\Vert \sum_{r\in\Gamma}c_{r}x_{r}\right\Vert =\left\Vert \sum_{r\in\Gamma}|c_{r}|x_{r}\right\Vert &\geq \frac{1}{m_{j_{0}}}\sum_{r\in\Gamma}f_{r}\left(\sum_{p\in\Gamma}|c_{p}|x_{p}\right) \\ &=\frac{1}{m_{j_{0}}}\sum_{r\in\Gamma}|c_{r}|f_{r}(x_{r})=\frac{1}{m_{j_{0}}}\sum_{r\in\Gamma}|c_{r}|\geq\frac{m_{1}-1}{m_{1}m_{j_{0}}}\sum_{r\in\Gamma}|c_{r}|, \end{align*} $$
and this completes the proof of the theorem.
4 Auxiliary Banach spaces and
 $c_{0}$
-type estimate
$c_{0}$
-type estimate
So far, we have proved that all spreading models admitted by normalized weakly null sequences in
![]() $X_{\mathcal {D}}$
are uniformly equivalent to the unit vector basis of
$X_{\mathcal {D}}$
are uniformly equivalent to the unit vector basis of
![]() $\ell _1$
. The remaining goal is to define in each subspace of
$\ell _1$
. The remaining goal is to define in each subspace of
![]() $X_{\mathcal {D}}$
a normalized collection
$X_{\mathcal {D}}$
a normalized collection
![]() $(x_\lambda )_{\lambda \in \mathcal {D}}$
satisfying the
$(x_\lambda )_{\lambda \in \mathcal {D}}$
satisfying the
![]() $\ell _\infty $
-estimate (1.1), and this will require some effort. As a first step, we define an auxiliary norming set
$\ell _\infty $
-estimate (1.1), and this will require some effort. As a first step, we define an auxiliary norming set
![]() $W^{\text {aux},\delta }$
inducing a norm on
$W^{\text {aux},\delta }$
inducing a norm on
![]() $c_{00}$
and an auxiliary Banach space
$c_{00}$
and an auxiliary Banach space
![]() $X_{\mathcal {D}}^{\text {aux},\delta }$
. We then prove estimates for the norm of linear combinations of “simple” vectors, specifically weighted
$X_{\mathcal {D}}^{\text {aux},\delta }$
. We then prove estimates for the norm of linear combinations of “simple” vectors, specifically weighted
![]() $(n,\varepsilon )$
basic special convex combinations, in the auxiliary space. These will be relevant later when a tool called the basic inequality will yield high-precision estimates of linear combinations of special sequences of vectors, called rapidly increasing sequences, in
$(n,\varepsilon )$
basic special convex combinations, in the auxiliary space. These will be relevant later when a tool called the basic inequality will yield high-precision estimates of linear combinations of special sequences of vectors, called rapidly increasing sequences, in
![]() $X_{\mathcal {D}}$
, in terms of sequences of basis vectors in
$X_{\mathcal {D}}$
, in terms of sequences of basis vectors in
![]() $X_{\mathcal {D}}^{\text {aux},\delta }$
.
$X_{\mathcal {D}}^{\text {aux},\delta }$
.
We derive in this section a
![]() $c_{0}$
-type estimate for the action of auxiliary functionals on weighted
$c_{0}$
-type estimate for the action of auxiliary functionals on weighted
![]() $(n,\varepsilon )$
-basic scc vectors. The idea is that the functional evaluates to something small if its weight is in some sense a mismatch to the
$(n,\varepsilon )$
-basic scc vectors. The idea is that the functional evaluates to something small if its weight is in some sense a mismatch to the
![]() $(n,\varepsilon )$
-basic scc vector weight. Let us first define the auxiliary functionals and auxiliary Banach spaces.
$(n,\varepsilon )$
-basic scc vector weight. Let us first define the auxiliary functionals and auxiliary Banach spaces.
We will define an auxiliary Banach space for each
![]() $\delta>0$
. First, fix
$\delta>0$
. First, fix
![]() $\delta>0$
and let
$\delta>0$
and let
![]() $W_{0}^{\text {aux},\delta }=\{\pm e_{i}^{*}\}_{i=1}^{\infty }\subset c_{00}$
as before. Then, also as before, define
$W_{0}^{\text {aux},\delta }=\{\pm e_{i}^{*}\}_{i=1}^{\infty }\subset c_{00}$
as before. Then, also as before, define
![]() $w(\pm e^{*}_{i})= m(\pm e^{*}_{i})=\infty $
and define the set of auxiliary weighted functionals
$w(\pm e^{*}_{i})= m(\pm e^{*}_{i})=\infty $
and define the set of auxiliary weighted functionals
 $$ \begin{align*} W^{\text{aux},\delta}_{1}=W^{\text{aux},\delta}_{0}\cup\left\{\frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{k=1}^{d}e^{*}_{i_{k}} \;\middle\vert\; \substack{ e^{*}_{i_{1}}<\ldots<e^{*}_{i_{d}} \text{ are } \\ S_{n_{j_{1}}+\cdots+n_{j_{l}}}\ast\mathcal{A}_{3}\text{-admissible}} \right\}, \end{align*} $$
$$ \begin{align*} W^{\text{aux},\delta}_{1}=W^{\text{aux},\delta}_{0}\cup\left\{\frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{k=1}^{d}e^{*}_{i_{k}} \;\middle\vert\; \substack{ e^{*}_{i_{1}}<\ldots<e^{*}_{i_{d}} \text{ are } \\ S_{n_{j_{1}}+\cdots+n_{j_{l}}}\ast\mathcal{A}_{3}\text{-admissible}} \right\}, \end{align*} $$
where
![]() $w(f)=m_{j_{1}}\cdots m_{j_{l}}$
,
$w(f)=m_{j_{1}}\cdots m_{j_{l}}$
,
![]() $m(f)=\max _{1\leq z\leq l}m_{j_{z}}$
, and
$m(f)=\max _{1\leq z\leq l}m_{j_{z}}$
, and
![]() $\vec w(f) = (m_{j_1},\ldots ,m_{j_\ell })$
, for
$\vec w(f) = (m_{j_1},\ldots ,m_{j_\ell })$
, for
![]() $f\in W_{1}^{\text {aux},\delta }\setminus W_{0}^{\text {aux},\delta }$
. We next define the following notion of proximity with respect to
$f\in W_{1}^{\text {aux},\delta }\setminus W_{0}^{\text {aux},\delta }$
. We next define the following notion of proximity with respect to
![]() $\overline {\mathcal {D}}$
for functionals in
$\overline {\mathcal {D}}$
for functionals in
![]() $W^{\text {aux},\delta }_{1}$
.
$W^{\text {aux},\delta }_{1}$
.
Definition 4.1 The functionals
![]() $f_{1}<\ldots <f_{d}$
in
$f_{1}<\ldots <f_{d}$
in
![]() $W^{\text {aux},\delta }_{1}$
are said to be
$W^{\text {aux},\delta }_{1}$
are said to be
![]() $(n,\lambda )_{\delta }$
-packed for some
$(n,\lambda )_{\delta }$
-packed for some
![]() $\lambda \in \overline {\mathcal {D}}$
if the following conditions are satisfied:
$\lambda \in \overline {\mathcal {D}}$
if the following conditions are satisfied:
-
(1)
 $f_{1}<\ldots <f_{d}$
are
$f_{1}<\ldots <f_{d}$
are
 $S_{n}\ast \mathcal {A}_{3}$
-admissible,
$S_{n}\ast \mathcal {A}_{3}$
-admissible, -
(2)
 $w(f_{i})\geq 2^{\max \text {supp}(f_{i-2})}$
for
$w(f_{i})\geq 2^{\max \text {supp}(f_{i-2})}$
for
 $3\leq i\leq d$
,
$3\leq i\leq d$
, -
(3)
 $d(m(f_{i}),\lambda )\leq \delta $
for
$d(m(f_{i}),\lambda )\leq \delta $
for
 $f_{i}\notin W^{\text {aux},\delta }_{0}$
and for
$f_{i}\notin W^{\text {aux},\delta }_{0}$
and for
 $2\leq i\leq d$
.
$2\leq i\leq d$
.
This definition is the base case for the following inductive definition.
Definition 4.2 The functionals
![]() $f_{1}<\ldots <f_{d}$
in
$f_{1}<\ldots <f_{d}$
in
![]() $W^{\text {aux},\delta }_{1}$
are said to be
$W^{\text {aux},\delta }_{1}$
are said to be
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},\lambda )_{\delta }$
-packed for some
$(n_{j_{1}},\ldots ,n_{j_{l}},\lambda )_{\delta }$
-packed for some
![]() $\lambda \in \overline {\mathcal {D}}$
if the following conditions hold:
$\lambda \in \overline {\mathcal {D}}$
if the following conditions hold:
-
(1)
 $w(f_{i})\geq 2^{\max \text {supp}(f_{i-2})}$
for
$w(f_{i})\geq 2^{\max \text {supp}(f_{i-2})}$
for
 $3\leq i\leq d$
,
$3\leq i\leq d$
, -
(2) There exists a partition
 $F_{1}<\ldots <F_{M}$
of
$F_{1}<\ldots <F_{M}$
of
 $\{1,\ldots ,d\}$
such that the set
$\{1,\ldots ,d\}$
such that the set
 $\{f_{\min (F_{k})}\}_{k=1}^{M}$
is
$\{f_{\min (F_{k})}\}_{k=1}^{M}$
is
 $S_{n_{j_{l}}}$
-admissible and such that the functionals
$S_{n_{j_{l}}}$
-admissible and such that the functionals
 $(f_{i})_{i\in F_{k}}$
are
$(f_{i})_{i\in F_{k}}$
are
 $S_{n_{j_{1}}+\cdots +n_{j_{l-1}}}\ast \mathcal {A}_{3}$
-admissible for
$S_{n_{j_{1}}+\cdots +n_{j_{l-1}}}\ast \mathcal {A}_{3}$
-admissible for
 $1\leq k\leq M$
,
$1\leq k\leq M$
, -
(3) There exists a node
 $\lambda _{1}\in \overline {\mathcal {D}}$
such that
$\lambda _{1}\in \overline {\mathcal {D}}$
such that
 $(f_{i})_{i\in F_{1}}$
is
$(f_{i})_{i\in F_{1}}$
is
 $(n_{j_{1}},\ldots ,n_{j_{l-1}},\lambda _{1})_{\delta }$
-packed,
$(n_{j_{1}},\ldots ,n_{j_{l-1}},\lambda _{1})_{\delta }$
-packed, -
(4)
 $d(m(f_{i}),\lambda )\leq \delta $
for
$d(m(f_{i}),\lambda )\leq \delta $
for
 $f_{i}\in \left (\bigcup _{k=2}^{M}F_{k}\right )\setminus W^{\text {aux},\delta }_{0}$
.
$f_{i}\in \left (\bigcup _{k=2}^{M}F_{k}\right )\setminus W^{\text {aux},\delta }_{0}$
.
It is worth noting that a subset of
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},\lambda )_{\delta }$
-packed functionals in
$(n_{j_{1}},\ldots ,n_{j_{l}},\lambda )_{\delta }$
-packed functionals in
![]() $W^{\text {aux},\delta }_{1}$
is still
$W^{\text {aux},\delta }_{1}$
is still
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},\lambda )_{\delta }$
-packed, and we now define the next set of auxiliary weighted functionals
$(n_{j_{1}},\ldots ,n_{j_{l}},\lambda )_{\delta }$
-packed, and we now define the next set of auxiliary weighted functionals
 $$ \begin{align*} W^{\text{aux},\delta}_{2}=W^{\text{aux},\delta}_{1}\cup\left\{ \frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{i=1}^{d}f_{i} \;\middle\vert\; \substack{ f_{1}<\ldots<f_{d} \text{ are in } W^{\text{aux},\delta}_{1} \text{ and are} \\ (n_{j_{1}},\ldots,n_{j_{l}},\lambda)_{\delta}\text{-packed for some } \lambda\in\overline{\mathcal{D}}} \right\} \end{align*} $$
$$ \begin{align*} W^{\text{aux},\delta}_{2}=W^{\text{aux},\delta}_{1}\cup\left\{ \frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{i=1}^{d}f_{i} \;\middle\vert\; \substack{ f_{1}<\ldots<f_{d} \text{ are in } W^{\text{aux},\delta}_{1} \text{ and are} \\ (n_{j_{1}},\ldots,n_{j_{l}},\lambda)_{\delta}\text{-packed for some } \lambda\in\overline{\mathcal{D}}} \right\} \end{align*} $$
with
![]() $w(f)=m_{j_{1}}\cdots m_{j_{l}}$
,
$w(f)=m_{j_{1}}\cdots m_{j_{l}}$
,
![]() $m(f)=\max _{1\leq z\leq l}m_{j_{z}}$
, and
$m(f)=\max _{1\leq z\leq l}m_{j_{z}}$
, and
![]() $\vec w(f) = (m_{j_1},\ldots ,m_{j_\ell })$
. Now, once we have defined the sets
$\vec w(f) = (m_{j_1},\ldots ,m_{j_\ell })$
. Now, once we have defined the sets
![]() $W^{\text {aux},\delta }_{0},W^{\text {aux},\delta }_{1},\ldots ,W^{\text {aux},\delta }_{k}$
, we replace
$W^{\text {aux},\delta }_{0},W^{\text {aux},\delta }_{1},\ldots ,W^{\text {aux},\delta }_{k}$
, we replace
![]() $W^{\text {aux},\delta }_{1}$
in Definitions 4.1 and 4.2 with
$W^{\text {aux},\delta }_{1}$
in Definitions 4.1 and 4.2 with
![]() $W^{\text {aux},\delta }_{k}$
and, we write that
$W^{\text {aux},\delta }_{k}$
and, we write that
 $$ \begin{align*} W^{\text{aux},\delta}_{k+1}=W^{\text{aux},\delta}_{k}\cup\left\{ \frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{i=1}^{d}f_{i} \;\middle\vert\; \substack{ f_{1}<\ldots<f_{d} \text{ are in } W^{\text{aux},\delta}_{k} \text{ and are} \\ (n_{j_{1}},\ldots,n_{j_{l}},\lambda)_{\delta}\text{-packed for some } \lambda\in\overline{\mathcal{D}}} \right\} \end{align*} $$
$$ \begin{align*} W^{\text{aux},\delta}_{k+1}=W^{\text{aux},\delta}_{k}\cup\left\{ \frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{i=1}^{d}f_{i} \;\middle\vert\; \substack{ f_{1}<\ldots<f_{d} \text{ are in } W^{\text{aux},\delta}_{k} \text{ and are} \\ (n_{j_{1}},\ldots,n_{j_{l}},\lambda)_{\delta}\text{-packed for some } \lambda\in\overline{\mathcal{D}}} \right\} \end{align*} $$
for each
![]() $k\in \mathbb {N}$
. We then define our norming set
$k\in \mathbb {N}$
. We then define our norming set
![]() $W^{\text {aux},\delta }=\bigcup _{k=0}^{\infty }W^{\text {aux},\delta }_{k}$
, and we let the Banach space
$W^{\text {aux},\delta }=\bigcup _{k=0}^{\infty }W^{\text {aux},\delta }_{k}$
, and we let the Banach space
![]() $X_{\mathcal {D}}^{\text {aux},\delta }$
be the completion of
$X_{\mathcal {D}}^{\text {aux},\delta }$
be the completion of
![]() $c_{00}$
with respect to the norm that is given by
$c_{00}$
with respect to the norm that is given by
![]() $\|x\|_{W^{\text {aux},\delta }}=\sup \{f(x) \mid f\in W^{\text {aux},\delta }\}$
for
$\|x\|_{W^{\text {aux},\delta }}=\sup \{f(x) \mid f\in W^{\text {aux},\delta }\}$
for
![]() $x\in c_{00}$
. We will need the following lemma before we can prove the main result of this section.
$x\in c_{00}$
. We will need the following lemma before we can prove the main result of this section.
Lemma 4.1 Let
![]() $f=\frac {1}{m_{j_{1}}\cdots m_{j_{l}}}\sum _{i=1}^{d}f_{i}\in W^{\text {aux},\delta }$
. Then,
$f=\frac {1}{m_{j_{1}}\cdots m_{j_{l}}}\sum _{i=1}^{d}f_{i}\in W^{\text {aux},\delta }$
. Then,
![]() $\{ i \mid f_{i}\notin W^{\text {aux},\delta }_{0}\}=E_{0}\cup E_{1}\cup \ldots \cup E_{l}$
, where
$\{ i \mid f_{i}\notin W^{\text {aux},\delta }_{0}\}=E_{0}\cup E_{1}\cup \ldots \cup E_{l}$
, where
![]() $\mathrm {card}(E_0)\leq 1$
and, for each
$\mathrm {card}(E_0)\leq 1$
and, for each
![]() $1\leq z\leq l$
,
$1\leq z\leq l$
,
![]() $(f_{i})_{i\in E_{z}}$
is
$(f_{i})_{i\in E_{z}}$
is
![]() $S_{n_{j_{1}}+\cdots +n_{j_{z}}}\ast \mathcal {A}_{3}$
-admissible and
$S_{n_{j_{1}}+\cdots +n_{j_{z}}}\ast \mathcal {A}_{3}$
-admissible and
![]() $\max _{i\in E_{z}}d_{T}(m(f_{i}),\lambda _{z})\leq \delta $
for some
$\max _{i\in E_{z}}d_{T}(m(f_{i}),\lambda _{z})\leq \delta $
for some
![]() $\lambda _{z}\in \overline {\mathcal {D}}$
.
$\lambda _{z}\in \overline {\mathcal {D}}$
.
Proof We proceed by induction on the length l of the tuple
![]() $(m_{j_{1}},\ldots ,m_{j_{l}})$
. If
$(m_{j_{1}},\ldots ,m_{j_{l}})$
. If
![]() $l=1$
, then
$l=1$
, then
![]() $f=\frac {1}{m_{j_{1}}}\sum _{i=1}^{d}f_{i}\in W^{\text {aux},\delta }_{k}$
for some
$f=\frac {1}{m_{j_{1}}}\sum _{i=1}^{d}f_{i}\in W^{\text {aux},\delta }_{k}$
for some
![]() $k\geq 1$
, and we put
$k\geq 1$
, and we put
 $$ \begin{align*} E_{0}&=\{1\}\setminus\{ i \mid f_{i}\in W^{\text{aux},\delta}_{0}\} \\ E_{1}&=\{2,\ldots,d\}\setminus \{i \mid f_{i}\in W^{\text{aux},\delta}_{0}\} \end{align*} $$
$$ \begin{align*} E_{0}&=\{1\}\setminus\{ i \mid f_{i}\in W^{\text{aux},\delta}_{0}\} \\ E_{1}&=\{2,\ldots,d\}\setminus \{i \mid f_{i}\in W^{\text{aux},\delta}_{0}\} \end{align*} $$
and note that, if
![]() $k=1$
, then
$k=1$
, then
![]() $E_{0}=E_{1}=\emptyset $
so that the result holds vacuously. Assume then that
$E_{0}=E_{1}=\emptyset $
so that the result holds vacuously. Assume then that
![]() $k> 1$
and note that
$k> 1$
and note that
![]() $f_{1}<\ldots <f_{d}$
are in
$f_{1}<\ldots <f_{d}$
are in
![]() $W^{\text {aux},\delta }_{k-1}$
and are
$W^{\text {aux},\delta }_{k-1}$
and are
![]() $(n_{j_{1}},\lambda )_{\delta }$
-packed for some
$(n_{j_{1}},\lambda )_{\delta }$
-packed for some
![]() $\lambda \in \overline {\mathcal {D}}$
. It therefore follows by definition that
$\lambda \in \overline {\mathcal {D}}$
. It therefore follows by definition that
![]() $(f_{i})_{i\in E_{1}}$
are
$(f_{i})_{i\in E_{1}}$
are
![]() $S_{n_{j_{1}}}\ast \mathcal {A}_{3}$
-admissible and that
$S_{n_{j_{1}}}\ast \mathcal {A}_{3}$
-admissible and that
![]() $\max _{i\in E_{1}}d(m(f_{i}),\lambda )\leq \delta $
.
$\max _{i\in E_{1}}d(m(f_{i}),\lambda )\leq \delta $
.
Assume now that the result holds for functionals of the form
![]() $f=\frac {1}{m_{j_{1}}\cdots m_{j_{l}}}\sum _{i=1}^{d}f_{i}\in W^{\text {aux},\delta }$
and let
$f=\frac {1}{m_{j_{1}}\cdots m_{j_{l}}}\sum _{i=1}^{d}f_{i}\in W^{\text {aux},\delta }$
and let
![]() $g=\frac {1}{m_{j_{1}}\cdots m_{j_{l}}m_{j_{l+1}}}\sum _{i=1}^{d}g_{i}\in W^{\text {aux},\delta }$
. As above, the result holds vacuously if
$g=\frac {1}{m_{j_{1}}\cdots m_{j_{l}}m_{j_{l+1}}}\sum _{i=1}^{d}g_{i}\in W^{\text {aux},\delta }$
. As above, the result holds vacuously if
![]() $g\in W^{\text {aux},\delta }_{1}$
, so assume that
$g\in W^{\text {aux},\delta }_{1}$
, so assume that
![]() $g\in W^{\text {aux},\delta }_{k}$
for some
$g\in W^{\text {aux},\delta }_{k}$
for some
![]() $k>1$
. In this case, we have that
$k>1$
. In this case, we have that
![]() $g_{1}<\ldots <g_{d}$
are in
$g_{1}<\ldots <g_{d}$
are in
![]() $W^{\text {aux},\delta }_{k-1}$
and are
$W^{\text {aux},\delta }_{k-1}$
and are
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},n_{j_{l+1}},\lambda )_{\delta }$
-packed for some
$(n_{j_{1}},\ldots ,n_{j_{l}},n_{j_{l+1}},\lambda )_{\delta }$
-packed for some
![]() $\lambda \in \overline {\mathcal {D}}$
. It follows that there is a partition
$\lambda \in \overline {\mathcal {D}}$
. It follows that there is a partition
![]() $F_{1}<\ldots <F_{M}$
of
$F_{1}<\ldots <F_{M}$
of
![]() $\{1,\ldots ,d\}$
as in Definition 4.2. Note that in particular that
$\{1,\ldots ,d\}$
as in Definition 4.2. Note that in particular that
![]() $(g_{i})_{i\in F_{1}}$
are
$(g_{i})_{i\in F_{1}}$
are
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},\lambda _{1})_{\delta }$
-packed for some
$(n_{j_{1}},\ldots ,n_{j_{l}},\lambda _{1})_{\delta }$
-packed for some
![]() $\lambda _{1}\in \overline {\mathcal {D}}$
so that the functional
$\lambda _{1}\in \overline {\mathcal {D}}$
so that the functional
![]() $\tilde {g}=\frac {1}{m_{j_{1}}\cdots m_{j_{l}}}\sum _{i\in F_{1}}g_{i}\in W^{\text {aux},\delta }$
. Then, by the inductive hypothesis, there are sets
$\tilde {g}=\frac {1}{m_{j_{1}}\cdots m_{j_{l}}}\sum _{i\in F_{1}}g_{i}\in W^{\text {aux},\delta }$
. Then, by the inductive hypothesis, there are sets
![]() $E_{0}\cup E_{1}\cup \ldots \cup E_{l}\subset F_{1}$
so that the required claim holds for
$E_{0}\cup E_{1}\cup \ldots \cup E_{l}\subset F_{1}$
so that the required claim holds for
![]() $\tilde {g}$
. Now, let
$\tilde {g}$
. Now, let
![]() $E_{l+1}=\left (\bigcup _{r=2}^{M}F_{r}\right )\setminus \{ i \mid g_{i}\in W^{\text {aux},\delta }_{0}\}$
, and it follows that the required claim holds for g itself so that the proof is complete.
$E_{l+1}=\left (\bigcup _{r=2}^{M}F_{r}\right )\setminus \{ i \mid g_{i}\in W^{\text {aux},\delta }_{0}\}$
, and it follows that the required claim holds for g itself so that the proof is complete.
We now derive the aforementioned
![]() $c_{0}$
-type estimate for auxiliary weighted functionals whose weights in some sense mismatch the weights of weighted
$c_{0}$
-type estimate for auxiliary weighted functionals whose weights in some sense mismatch the weights of weighted
![]() $(n,\varepsilon )$
-basic scc vectors. First, we make a remark about the relation between the weight of a functional and the admissibility of its components.
$(n,\varepsilon )$
-basic scc vectors. First, we make a remark about the relation between the weight of a functional and the admissibility of its components.
Remark 4.2 Let
![]() $j\in \mathbb {N}$
and
$j\in \mathbb {N}$
and
![]() $f\in W$
such that
$f\in W$
such that
![]() $m(f)<m_j$
and
$m(f)<m_j$
and
![]() $w(f) < m_j^4$
. Then, if
$w(f) < m_j^4$
. Then, if
![]() $\vec w(f)= (m_{j_1},\ldots ,m_{j_\ell })$
,
$\vec w(f)= (m_{j_1},\ldots ,m_{j_\ell })$
,
![]() $n_{j_1}+\cdots +n_{j_\ell } < n_j$
. Indeed,
$n_{j_1}+\cdots +n_{j_\ell } < n_j$
. Indeed,
![]() $m_{1}^{l}\leq w(f) <m_{j}^{4}$
, and thus,
$m_{1}^{l}\leq w(f) <m_{j}^{4}$
, and thus,
![]() $l<4\log (m_{j})/\log (100)$
. By condition (2) on page 8,
$l<4\log (m_{j})/\log (100)$
. By condition (2) on page 8,
 $$\begin{align*}n_{j_{1}}+\cdots+n_{j_{l}}\leq ln_{j-1}< n_{j-1}4\frac{\log(m_{j})}{\log(100)}\leq n_{j}.\end{align*}$$
$$\begin{align*}n_{j_{1}}+\cdots+n_{j_{l}}\leq ln_{j-1}< n_{j-1}4\frac{\log(m_{j})}{\log(100)}\leq n_{j}.\end{align*}$$
Proposition 4.3 Let
![]() $N\in \mathbb {N}\cup \{0\}$
and choose
$N\in \mathbb {N}\cup \{0\}$
and choose
![]() $(t_{i})_{i=1}^{2^{N}}$
such that
$(t_{i})_{i=1}^{2^{N}}$
such that
![]() $d(m_{t_{i}},m_{t_{i'}})\geq 2^{-N}$
for each
$d(m_{t_{i}},m_{t_{i'}})\geq 2^{-N}$
for each
![]() $i\neq i'$
. Then, choose
$i\neq i'$
. Then, choose
![]() $\varepsilon _{i}\in \left (0,\frac {1}{3m_{t_{i}}2^{N}}\right )$
and define a
$\varepsilon _{i}\in \left (0,\frac {1}{3m_{t_{i}}2^{N}}\right )$
and define a
![]() $(n_{t_{i}},\varepsilon _{i})$
-basic scc by
$(n_{t_{i}},\varepsilon _{i})$
-basic scc by
for each
![]() $1\leq i\leq 2^{N}$
. It follows that
$1\leq i\leq 2^{N}$
. It follows that
![]() $\left \vert f\left (\sum _{i\in \Omega }a_{i}x_{i}\right )\right \vert \leq \left (1+\frac {4}{\sqrt {w(f)}}\right )\max _{i\in \Omega }|a_{i}|$
for every subset
$\left \vert f\left (\sum _{i\in \Omega }a_{i}x_{i}\right )\right \vert \leq \left (1+\frac {4}{\sqrt {w(f)}}\right )\max _{i\in \Omega }|a_{i}|$
for every subset
![]() $\Omega \subset \{1,\ldots ,2^{N}\}$
, for every choice
$\Omega \subset \{1,\ldots ,2^{N}\}$
, for every choice
![]() $(a_{i})_{i\in \Omega }$
of scalars, and for every auxiliary weighted functional
$(a_{i})_{i\in \Omega }$
of scalars, and for every auxiliary weighted functional
![]() $f=\frac {1}{m_{j_{1}}\cdots m_{j_{l}}}\sum _{q=1}^{d}f_{q}\in W^{\text {aux},\delta }$
where
$f=\frac {1}{m_{j_{1}}\cdots m_{j_{l}}}\sum _{q=1}^{d}f_{q}\in W^{\text {aux},\delta }$
where
![]() $\delta <2^{-(N+1)}$
.
$\delta <2^{-(N+1)}$
.
Proof Let
![]() $\Omega \subset \{1,\ldots ,2^{N}\}$
be given. We will proceed by induction on the level k norming sets
$\Omega \subset \{1,\ldots ,2^{N}\}$
be given. We will proceed by induction on the level k norming sets
![]() $W^{\text {aux},\delta }_{k}$
, and the inductive hypothesis will include that
$W^{\text {aux},\delta }_{k}$
, and the inductive hypothesis will include that
![]() $\left \vert f\left (\sum _{i\in A_{f}(\Omega )}a_{i}x_{i}\right )\right \vert <\frac {4\gamma }{\sqrt {w(f)}}$
if
$\left \vert f\left (\sum _{i\in A_{f}(\Omega )}a_{i}x_{i}\right )\right \vert <\frac {4\gamma }{\sqrt {w(f)}}$
if
![]() $f\notin W_{0}^{\text {aux},\delta }$
, where
$f\notin W_{0}^{\text {aux},\delta }$
, where
![]() $\gamma =\max _{i\in \Omega }|a_{i}|$
and where
$\gamma =\max _{i\in \Omega }|a_{i}|$
and where
![]() $A_{f}(\Omega ) :=\{i\in \Omega \mid m_{t_{i}}\neq m(f)\}$
. The base case is the level
$A_{f}(\Omega ) :=\{i\in \Omega \mid m_{t_{i}}\neq m(f)\}$
. The base case is the level
![]() $k=1$
norming set, and we first let
$k=1$
norming set, and we first let
![]() $f\in W^{\text {aux},\delta }_{0}$
so that
$f\in W^{\text {aux},\delta }_{0}$
so that
 $$ \begin{align*} \left\vert f\left(\sum_{i\in\Omega}a_{i}x_{i}\right)\right\vert = \left\vert e^{*}_{i_{0}}\left(\sum_{i\in\Omega}a_{i}m_{t_{i}}\sum_{r\in F_{i}}c^{i}_{r}e_{r} \right)\right\vert \leq \max_{i\in\Omega}\varepsilon_{i}m_{t_{i}}|a_{i}| < \max_{i\in\Omega}|a_{i}| \end{align*} $$
$$ \begin{align*} \left\vert f\left(\sum_{i\in\Omega}a_{i}x_{i}\right)\right\vert = \left\vert e^{*}_{i_{0}}\left(\sum_{i\in\Omega}a_{i}m_{t_{i}}\sum_{r\in F_{i}}c^{i}_{r}e_{r} \right)\right\vert \leq \max_{i\in\Omega}\varepsilon_{i}m_{t_{i}}|a_{i}| < \max_{i\in\Omega}|a_{i}| \end{align*} $$
for some
![]() $i_{0}\in \mathbb {N}$
. It therefore remains to check functionals of the form
$i_{0}\in \mathbb {N}$
. It therefore remains to check functionals of the form
 $$ \begin{align*} f=\frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{q=1}^{d}e^{*}_{i_{q}}\in W^{\text{aux},\delta}_{1}\setminus W^{\text{aux},\delta}_{0}, \end{align*} $$
$$ \begin{align*} f=\frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{q=1}^{d}e^{*}_{i_{q}}\in W^{\text{aux},\delta}_{1}\setminus W^{\text{aux},\delta}_{0}, \end{align*} $$
and we write
![]() $A_{f}(\Omega )=\{ i\in \Omega \mid m_{t_{i}}\neq m(f)\}=A_{1}\cup A_{2}\cup A_{3}$
, where
$A_{f}(\Omega )=\{ i\in \Omega \mid m_{t_{i}}\neq m(f)\}=A_{1}\cup A_{2}\cup A_{3}$
, where
 $$ \begin{align*} A_{1}&=\{ i\in\Omega \mid m_{t_{i}}<m(f)\} \\ A_{2}&=\{ i\in\Omega \mid m(f)<m_{t_{i}}\text{ and } n_{j_{1}}+\cdots+n_{j_{l}}<n_{t_{i}}\} \\ A_{3}&=\{ i\in\Omega \mid m(f)<m_{t_{i}} \text{ and } n_{j_{1}}+\cdots+n_{j_{l}}\geq n_{t_{i}}\} \end{align*} $$
$$ \begin{align*} A_{1}&=\{ i\in\Omega \mid m_{t_{i}}<m(f)\} \\ A_{2}&=\{ i\in\Omega \mid m(f)<m_{t_{i}}\text{ and } n_{j_{1}}+\cdots+n_{j_{l}}<n_{t_{i}}\} \\ A_{3}&=\{ i\in\Omega \mid m(f)<m_{t_{i}} \text{ and } n_{j_{1}}+\cdots+n_{j_{l}}\geq n_{t_{i}}\} \end{align*} $$
so that
![]() $\Omega \setminus A_{f}(\Omega )$
is at most a singleton
$\Omega \setminus A_{f}(\Omega )$
is at most a singleton
![]() $\{i_{0}\}$
with
$\{i_{0}\}$
with
![]() $m_{t_{i_{0}}}=m(f)$
. Then, we have that
$m_{t_{i_{0}}}=m(f)$
. Then, we have that
 $$ \begin{align*} \left\vert f\left(\sum_{i\in\Omega}a_{i}x_{i}\right)\right\vert\leq \sum_{p=1}^{3}\left\vert f\left(\sum_{i\in A_{p}}a_{i}x_{i}\right)\right\vert + |f(a_{i_{0}}x_{i_{0}})|\leq \sum_{p=1}^{3}\left\vert f\left(\sum_{i\in A_{p}}a_{i}x_{i}\right)\right\vert + \max_{i\in\Omega}|a_{i}| \end{align*} $$
$$ \begin{align*} \left\vert f\left(\sum_{i\in\Omega}a_{i}x_{i}\right)\right\vert\leq \sum_{p=1}^{3}\left\vert f\left(\sum_{i\in A_{p}}a_{i}x_{i}\right)\right\vert + |f(a_{i_{0}}x_{i_{0}})|\leq \sum_{p=1}^{3}\left\vert f\left(\sum_{i\in A_{p}}a_{i}x_{i}\right)\right\vert + \max_{i\in\Omega}|a_{i}| \end{align*} $$
because
![]() $|f(x_{i_{0}})|\leq \frac {m_{t_{i_{0}}}}{w(f)}\leq 1$
. Now, recall that
$|f(x_{i_{0}})|\leq \frac {m_{t_{i_{0}}}}{w(f)}\leq 1$
. Now, recall that
![]() $\gamma =\max _{i\in \Omega }|a_{i}|$
and note that, for
$\gamma =\max _{i\in \Omega }|a_{i}|$
and note that, for
![]() $A_{1}$
, there is the estimate
$A_{1}$
, there is the estimate
 $$ \begin{align*} \left\vert f\left(\sum_{i\in A_{1}}a_{i}x_{i}\right)\right\vert&\leq \sum_{i\in A_{1}}|f(a_{i}x_{i})|\leq \frac{\gamma}{w(f)}\sum_{i\in A_{1}}m_{t_{i}} \\ &\leq \frac{\gamma}{w(f)}\text{card}(A_{1})m_{t_{\max(A_{1})}} \leq \frac{\gamma}{w(f)}t_{\max(A_{1})}m_{t_{\max(A_{1})}} \\ &\leq \frac{\gamma}{w(f)}(\text{ind}(m(f))-1)m_{\text{ind}(m(f))-1} \leq \frac{\gamma m_{\text{ind}(m(f))}}{w(f)\sqrt{m_{\text{ind}(m(f))}}} \leq \frac{\gamma}{\sqrt{w(f)}},\end{align*} $$
$$ \begin{align*} \left\vert f\left(\sum_{i\in A_{1}}a_{i}x_{i}\right)\right\vert&\leq \sum_{i\in A_{1}}|f(a_{i}x_{i})|\leq \frac{\gamma}{w(f)}\sum_{i\in A_{1}}m_{t_{i}} \\ &\leq \frac{\gamma}{w(f)}\text{card}(A_{1})m_{t_{\max(A_{1})}} \leq \frac{\gamma}{w(f)}t_{\max(A_{1})}m_{t_{\max(A_{1})}} \\ &\leq \frac{\gamma}{w(f)}(\text{ind}(m(f))-1)m_{\text{ind}(m(f))-1} \leq \frac{\gamma m_{\text{ind}(m(f))}}{w(f)\sqrt{m_{\text{ind}(m(f))}}} \leq \frac{\gamma}{\sqrt{w(f)}},\end{align*} $$
where we have used the first condition on the sequence
![]() $(m_{j})$
and the fact that
$(m_{j})$
and the fact that
![]() $t_{i}<\text {ind}(m(f)):=\max _{1\leq z\leq l}j_{z}$
for each
$t_{i}<\text {ind}(m(f)):=\max _{1\leq z\leq l}j_{z}$
for each
![]() $i\in A_{1}$
. Next, for
$i\in A_{1}$
. Next, for
![]() $A_{2}$
, note that
$A_{2}$
, note that
 $$ \begin{align*} \left\vert f\left(\sum_{i\in A_{2}}a_{i}x_{i}\right)\right\vert &\leq \frac{\gamma}{w(f)}\sum_{i\in A_{2}}m_{t_{i}}\left\vert\sum_{q=1}^{d}e^{*}_{i_{q}}\left(\sum_{r\in F_{i}}c^{i}_{r}e_{r}\right) \right\vert \\ &\leq \frac{\gamma}{w(f)}\sum_{i\in A_{2}} 3m_{t_{i}}\varepsilon_{i} \leq\frac{\gamma}{w(f)}\sum_{i\in A_{2}}\frac{1}{2^{N}}\leq\frac{\gamma}{w(f)}\leq\frac{\gamma}{\sqrt{w(f)}}, \end{align*} $$
$$ \begin{align*} \left\vert f\left(\sum_{i\in A_{2}}a_{i}x_{i}\right)\right\vert &\leq \frac{\gamma}{w(f)}\sum_{i\in A_{2}}m_{t_{i}}\left\vert\sum_{q=1}^{d}e^{*}_{i_{q}}\left(\sum_{r\in F_{i}}c^{i}_{r}e_{r}\right) \right\vert \\ &\leq \frac{\gamma}{w(f)}\sum_{i\in A_{2}} 3m_{t_{i}}\varepsilon_{i} \leq\frac{\gamma}{w(f)}\sum_{i\in A_{2}}\frac{1}{2^{N}}\leq\frac{\gamma}{w(f)}\leq\frac{\gamma}{\sqrt{w(f)}}, \end{align*} $$
where we have used the observation that immediately precedes Proposition 2.1 and the fact that
![]() $e^{*}_{i_{1}}<\ldots <e^{*}_{i_{d}}$
are
$e^{*}_{i_{1}}<\ldots <e^{*}_{i_{d}}$
are
![]() $S_{n_{j_{1}}+\cdots +n_{j_{l}}}\ast \mathcal {A}_{3}$
-admissible with
$S_{n_{j_{1}}+\cdots +n_{j_{l}}}\ast \mathcal {A}_{3}$
-admissible with
![]() $n_{j_{1}}+\cdots +n_{j_{l}}<n_{t_{i}}$
for each
$n_{j_{1}}+\cdots +n_{j_{l}}<n_{t_{i}}$
for each
![]() $i\in A_{2}$
. Lastly, for
$i\in A_{2}$
. Lastly, for
![]() $A_{3}$
, note that
$A_{3}$
, note that
 $$ \begin{align*} \left\vert f\left(\sum_{i\in A_{3}}a_{i}x_{i}\right)\right\vert &\leq \frac{\gamma}{w(f)}\sum_{i\in A_{3}}m_{t_{i}} \leq \frac{\gamma}{w(f)}|A_{3}|m_{t_{\max(A_{3})}} \\ &\leq\frac{\gamma m^{2}_{t_{\max(A_{3})}}}{w(f)}\leq \frac{\gamma\sqrt{w(f)}}{w(f)}=\frac{\gamma}{\sqrt{w(f)}}\end{align*} $$
$$ \begin{align*} \left\vert f\left(\sum_{i\in A_{3}}a_{i}x_{i}\right)\right\vert &\leq \frac{\gamma}{w(f)}\sum_{i\in A_{3}}m_{t_{i}} \leq \frac{\gamma}{w(f)}|A_{3}|m_{t_{\max(A_{3})}} \\ &\leq\frac{\gamma m^{2}_{t_{\max(A_{3})}}}{w(f)}\leq \frac{\gamma\sqrt{w(f)}}{w(f)}=\frac{\gamma}{\sqrt{w(f)}}\end{align*} $$
because
![]() $m_{t_{i}}^{2}\leq \sqrt {w(f)}$
for each
$m_{t_{i}}^{2}\leq \sqrt {w(f)}$
for each
![]() $i\in A_{3}$
, by Remark 4.2. It now follows by putting these pieces together that
$i\in A_{3}$
, by Remark 4.2. It now follows by putting these pieces together that
 $$ \begin{align*} \left\vert f\left(\sum_{i\in\Omega}a_{i}x_{i}\right)\right\vert \leq \gamma+\frac{3\gamma}{\sqrt{w(f)}}\end{align*} $$
$$ \begin{align*} \left\vert f\left(\sum_{i\in\Omega}a_{i}x_{i}\right)\right\vert \leq \gamma+\frac{3\gamma}{\sqrt{w(f)}}\end{align*} $$
for each
![]() $f\in W^{\text {aux},\delta }_{1}$
, and, in particular, we have that
$f\in W^{\text {aux},\delta }_{1}$
, and, in particular, we have that
![]() $\left \vert f\left (\sum _{i\in A_{f}(\Omega )}a_{i}x_{i}\right )\right \vert < \frac {4\gamma }{\sqrt {w(f)}}$
, as is required as part of the inductive hypothesis.
$\left \vert f\left (\sum _{i\in A_{f}(\Omega )}a_{i}x_{i}\right )\right \vert < \frac {4\gamma }{\sqrt {w(f)}}$
, as is required as part of the inductive hypothesis.
Assume now that the statement of Proposition 4.3 holds for every functional
![]() $f\in W^{\text {aux},\delta }_{k}$
, let
$f\in W^{\text {aux},\delta }_{k}$
, let
![]() $\Omega \subset \{1,\ldots ,2^{N}\}$
be given, and let
$\Omega \subset \{1,\ldots ,2^{N}\}$
be given, and let
 $$ \begin{align*} f=\frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{q=1}^{d}f_{q}\in W^{\text{aux},\delta}_{k+1}\setminus W^{\text{aux},\delta}_{k}, \end{align*} $$
$$ \begin{align*} f=\frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{q=1}^{d}f_{q}\in W^{\text{aux},\delta}_{k+1}\setminus W^{\text{aux},\delta}_{k}, \end{align*} $$
where
![]() $f_{q}\in W^{\text {aux},\delta }_{k}$
for each
$f_{q}\in W^{\text {aux},\delta }_{k}$
for each
![]() $1\leq q\leq d$
. Define the sets
$1\leq q\leq d$
. Define the sets
![]() $B=\{q \mid f_{q}\in W^{\text {aux},\delta }_{0}\}$
and
$B=\{q \mid f_{q}\in W^{\text {aux},\delta }_{0}\}$
and
![]() $C=\{3,\ldots ,d\}\setminus B$
. We may then write
$C=\{3,\ldots ,d\}\setminus B$
. We may then write
![]() $f=\sum _{\alpha =1}^{4}g_{\alpha }$
, where
$f=\sum _{\alpha =1}^{4}g_{\alpha }$
, where
 $$ \begin{align*} g_{1}=\frac{1}{w(f)}f_{1},\text{ }g_{2}=\frac{1}{w(f)}f_{2},\text{ }g_{3}=\frac{1}{w(f)}\sum_{q\in B}f_{q}, \text{ and } g_{4}=\frac{1}{w(f)}\sum_{q\in C}f_{q}, \end{align*} $$
$$ \begin{align*} g_{1}=\frac{1}{w(f)}f_{1},\text{ }g_{2}=\frac{1}{w(f)}f_{2},\text{ }g_{3}=\frac{1}{w(f)}\sum_{q\in B}f_{q}, \text{ and } g_{4}=\frac{1}{w(f)}\sum_{q\in C}f_{q}, \end{align*} $$
and it follows that
 $$ \begin{align*} \left\vert f\left(\sum_{i\in\Omega}a_{i}x_{i}\right)\right\vert \leq \left\vert f\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert + |f(a_{i_{0}}x_{i_{0}})| \leq \max_{i\in\Omega}|a_{i}|+\left\vert f\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert, \end{align*} $$
$$ \begin{align*} \left\vert f\left(\sum_{i\in\Omega}a_{i}x_{i}\right)\right\vert \leq \left\vert f\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert + |f(a_{i_{0}}x_{i_{0}})| \leq \max_{i\in\Omega}|a_{i}|+\left\vert f\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert, \end{align*} $$
where, as before,
![]() $A_{f}(\Omega )=\{ i\in \Omega \mid m_{t_{i}}\neq m(f)\}$
so that
$A_{f}(\Omega )=\{ i\in \Omega \mid m_{t_{i}}\neq m(f)\}$
so that
![]() $\Omega \setminus A_{f}(\Omega )$
is at most a singleton
$\Omega \setminus A_{f}(\Omega )$
is at most a singleton
![]() $\{i_{0}\}$
with
$\{i_{0}\}$
with
![]() $m_{t_{i_{0}}}=m(f)$
, in which case,
$m_{t_{i_{0}}}=m(f)$
, in which case,
![]() $|f(x_{i_{0}})|\leq \frac {m_{t_{i_{0}}}}{w(f)}\leq 1$
. Let
$|f(x_{i_{0}})|\leq \frac {m_{t_{i_{0}}}}{w(f)}\leq 1$
. Let
![]() $\gamma =\max _{i\in \Omega }|a_{i}|$
as before, and it now remains to estimate
$\gamma =\max _{i\in \Omega }|a_{i}|$
as before, and it now remains to estimate
 $$ \begin{align*} \left\vert f\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert&\leq \sum_{\alpha=1}^{4}\left\vert g_{\alpha}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert \\ &\leq\frac{1}{w(f)}\left\vert f_{1}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert + \frac{1}{w(f)}\left\vert f_{2}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert \\ &\qquad + \frac{1}{w(f)}\left\vert \sum_{q\in B}f_{q}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert + \frac{1}{w(f)}\left\vert\sum_{q\in C}f_{q}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert, \end{align*} $$
$$ \begin{align*} \left\vert f\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert&\leq \sum_{\alpha=1}^{4}\left\vert g_{\alpha}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert \\ &\leq\frac{1}{w(f)}\left\vert f_{1}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert + \frac{1}{w(f)}\left\vert f_{2}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert \\ &\qquad + \frac{1}{w(f)}\left\vert \sum_{q\in B}f_{q}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert + \frac{1}{w(f)}\left\vert\sum_{q\in C}f_{q}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert, \end{align*} $$
where, after applying the inductive hypothesis to the
![]() $g_{1}$
and
$g_{1}$
and
![]() $g_{2}$
terms and using the same argument as is used in the base case for the
$g_{2}$
terms and using the same argument as is used in the base case for the
![]() $g_{3}$
term, this quantity is bounded above by
$g_{3}$
term, this quantity is bounded above by
 $$ \begin{align*} &\frac{\gamma}{w(f)}\left(1+\frac{3}{\sqrt{w(f_{1})}}\right)+\frac{\gamma}{w(f)}\left(1+\frac{3}{\sqrt{w(f_{2})}}\right) +\frac{3\gamma}{\sqrt{w(f)}}+\frac{1}{w(f)}\left\vert \sum_{q\in C}f_{q}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert \\ &\qquad\leq \frac{\frac{13}{5}\gamma}{w(f)}+\frac{3\gamma}{\sqrt{w(f)}}+\frac{1}{w(f)}\left\vert\sum_{q\in C}f_{q}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert \\ &\qquad\leq \frac{(3+\frac{13}{50})\gamma}{\sqrt{w(f)}}+ \frac{1}{w(f)}\left\vert\sum_{q\in C}f_{q}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert \end{align*} $$
$$ \begin{align*} &\frac{\gamma}{w(f)}\left(1+\frac{3}{\sqrt{w(f_{1})}}\right)+\frac{\gamma}{w(f)}\left(1+\frac{3}{\sqrt{w(f_{2})}}\right) +\frac{3\gamma}{\sqrt{w(f)}}+\frac{1}{w(f)}\left\vert \sum_{q\in C}f_{q}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert \\ &\qquad\leq \frac{\frac{13}{5}\gamma}{w(f)}+\frac{3\gamma}{\sqrt{w(f)}}+\frac{1}{w(f)}\left\vert\sum_{q\in C}f_{q}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert \\ &\qquad\leq \frac{(3+\frac{13}{50})\gamma}{\sqrt{w(f)}}+ \frac{1}{w(f)}\left\vert\sum_{q\in C}f_{q}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert \end{align*} $$
because
![]() $m_{1}\geq 100$
. Now, note that there are sets
$m_{1}\geq 100$
. Now, note that there are sets
![]() $E_{0}\cup E_{1}\cup \ldots \cup E_{l}$
from Lemma 4.1 such that
$E_{0}\cup E_{1}\cup \ldots \cup E_{l}$
from Lemma 4.1 such that
![]() $\{q \mid f_{q}\in \mathcal {C}\}=E_{0}\cup E_{1}\cup \ldots \cup E_{l}$
and such that, for each
$\{q \mid f_{q}\in \mathcal {C}\}=E_{0}\cup E_{1}\cup \ldots \cup E_{l}$
and such that, for each
![]() $1\leq z\leq l$
, we have that
$1\leq z\leq l$
, we have that
![]() $(f_{q})_{q\in E_{z}}$
is
$(f_{q})_{q\in E_{z}}$
is
![]() $S_{n_{j_{1}}+\cdots +n_{j_{z}}}\ast \mathcal {A}_{3}$
-admissible and
$S_{n_{j_{1}}+\cdots +n_{j_{z}}}\ast \mathcal {A}_{3}$
-admissible and
![]() $\max _{q\in E_{z}}d(m(f_{q}),\lambda _{z})\leq \delta $
for some
$\max _{q\in E_{z}}d(m(f_{q}),\lambda _{z})\leq \delta $
for some
![]() $\lambda _{z}\in \overline {\mathcal {D}}$
. Next, let
$\lambda _{z}\in \overline {\mathcal {D}}$
. Next, let
![]() $\Gamma _{z}=\{ i\in A_{f}(\Omega ) \mid m_{t_{i}}=m(f_{q}) \text { for some } q\in E_{z}\}$
for each
$\Gamma _{z}=\{ i\in A_{f}(\Omega ) \mid m_{t_{i}}=m(f_{q}) \text { for some } q\in E_{z}\}$
for each
![]() $1\leq z\leq l$
and note that if
$1\leq z\leq l$
and note that if
![]() $i_{1},i_{2}\in \Gamma _{z}$
, then we have that
$i_{1},i_{2}\in \Gamma _{z}$
, then we have that
 $$ \begin{align*} 2^{-N} &\leq d(m_{t_{i_{1}}},m_{t_{i_{2}}}) \\ &= d(m(f_{q_{1}}),m(f_{q_{2}}))\leq d(m(f_{q_{1}}),\lambda_{z})+d(\lambda_{z},m(f_{q_{2}})) \leq 2\delta \end{align*} $$
$$ \begin{align*} 2^{-N} &\leq d(m_{t_{i_{1}}},m_{t_{i_{2}}}) \\ &= d(m(f_{q_{1}}),m(f_{q_{2}}))\leq d(m(f_{q_{1}}),\lambda_{z})+d(\lambda_{z},m(f_{q_{2}})) \leq 2\delta \end{align*} $$
for the corresponding
![]() $q_{1},q_{2}\in E_{z}$
, and this cannot happen. It follows that
$q_{1},q_{2}\in E_{z}$
, and this cannot happen. It follows that
![]() $\Gamma _{z}$
is at most a singleton, say
$\Gamma _{z}$
is at most a singleton, say
![]() $i_{z}$
, for each
$i_{z}$
, for each
![]() $1\leq z\leq l$
so that
$1\leq z\leq l$
so that
 $$ \begin{align*}\left\vert \sum_{q\in\mathcal{C}}f_{q}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert &\leq \sum_{z=0}^{l} \sum_{q\in E_{z}} \left\vert f_{q}\left(\sum_{i \in A_{f}(\Omega)\setminus\{i_{z}\}}a_{i}x_{i}\right)\right\vert + \sum_{z=0}^{l}\sum_{q\in E_{z}}|f_{q}(a_{i_{z}}x_{i_{z}})| \\ &\leq \sum_{z=0}^{l}\sum_{q\in E_{z}}\frac{4\gamma}{\sqrt{w(f_{q})}} + \gamma\sum_{z=0}^{l}\sum_{q\in E_{z}}\frac{m_{t_{i_{z}}}}{w(f_{q})} \\ &\leq (l+1)\gamma + \sum_{z=0}^{l}\sum_{q\in E_{z}}\frac{4\gamma}{\sqrt{w(f_{q})}} \leq (l+5)\gamma, \end{align*} $$
$$ \begin{align*}\left\vert \sum_{q\in\mathcal{C}}f_{q}\left(\sum_{i\in A_{f}(\Omega)}a_{i}x_{i}\right)\right\vert &\leq \sum_{z=0}^{l} \sum_{q\in E_{z}} \left\vert f_{q}\left(\sum_{i \in A_{f}(\Omega)\setminus\{i_{z}\}}a_{i}x_{i}\right)\right\vert + \sum_{z=0}^{l}\sum_{q\in E_{z}}|f_{q}(a_{i_{z}}x_{i_{z}})| \\ &\leq \sum_{z=0}^{l}\sum_{q\in E_{z}}\frac{4\gamma}{\sqrt{w(f_{q})}} + \gamma\sum_{z=0}^{l}\sum_{q\in E_{z}}\frac{m_{t_{i_{z}}}}{w(f_{q})} \\ &\leq (l+1)\gamma + \sum_{z=0}^{l}\sum_{q\in E_{z}}\frac{4\gamma}{\sqrt{w(f_{q})}} \leq (l+5)\gamma, \end{align*} $$
where again, we have used the inductive hypothesis, and, by putting all of these pieces together, there is the estimate
 $$ \begin{align*} \left\vert f\left(\sum_{i\in\Omega}a_{i}x_{i}\right)\right\vert &\leq \gamma+\frac{(3+\frac{13}{50})\gamma}{\sqrt{w(f)}}+\frac{(l+5)\gamma}{w(f)} \\ &\leq \gamma+\frac{(3+\frac{13}{50})\gamma}{\sqrt{w(f)}}+\frac{(l+5)\gamma}{10^{l}\sqrt{w(f)}} \leq \gamma + \frac{(3+\frac{13}{50}+\frac{3}{5})\gamma}{\sqrt{w(f)}} \leq \gamma+ \frac{4\gamma}{\sqrt{w(f)}},\end{align*} $$
$$ \begin{align*} \left\vert f\left(\sum_{i\in\Omega}a_{i}x_{i}\right)\right\vert &\leq \gamma+\frac{(3+\frac{13}{50})\gamma}{\sqrt{w(f)}}+\frac{(l+5)\gamma}{w(f)} \\ &\leq \gamma+\frac{(3+\frac{13}{50})\gamma}{\sqrt{w(f)}}+\frac{(l+5)\gamma}{10^{l}\sqrt{w(f)}} \leq \gamma + \frac{(3+\frac{13}{50}+\frac{3}{5})\gamma}{\sqrt{w(f)}} \leq \gamma+ \frac{4\gamma}{\sqrt{w(f)}},\end{align*} $$
where, in particular,
![]() $\left \vert f\left (\sum _{i\in A_{f}(\Omega )}a_{i}x_{i}\right )\right \vert \leq \frac {4\gamma }{\sqrt {w(f)}} $
so that the proof is complete.
$\left \vert f\left (\sum _{i\in A_{f}(\Omega )}a_{i}x_{i}\right )\right \vert \leq \frac {4\gamma }{\sqrt {w(f)}} $
so that the proof is complete.
5 Rapidly increasing sequences and basic inequality
Rapidly increasing sequences (RISs) and the basic inequality are standard concepts used in most Banach spaces constructions using saturated norms, such as
![]() $X_{\mathcal {D}}$
. The main utility of such sequences is that they can be found in every infinite-dimensional subspace of
$X_{\mathcal {D}}$
. The main utility of such sequences is that they can be found in every infinite-dimensional subspace of
![]() $X_{\mathcal {D}}$
, and, via the basic inequality, the norm of their linear combinations is bounded above by the same linear combinations of basis vectors in the auxiliary space
$X_{\mathcal {D}}$
, and, via the basic inequality, the norm of their linear combinations is bounded above by the same linear combinations of basis vectors in the auxiliary space
![]() $X_{\mathcal {D}}^{\mathrm {aux},\delta }$
. RISs first appeared in [Reference Schlumprecht26], and the basic inequality has its roots in [Reference Argyros and Deliyanni1]. These tools will be essential in Section 6 when we construct, in an arbitrary infinite-dimensional block subspace of
$X_{\mathcal {D}}^{\mathrm {aux},\delta }$
. RISs first appeared in [Reference Schlumprecht26], and the basic inequality has its roots in [Reference Argyros and Deliyanni1]. These tools will be essential in Section 6 when we construct, in an arbitrary infinite-dimensional block subspace of
![]() $X_{\mathcal {D}}$
, a tree of normalized vectors that witness the failure of the Lebesgue property.
$X_{\mathcal {D}}$
, a tree of normalized vectors that witness the failure of the Lebesgue property.
We begin with a short technical lemma, and we recall that
![]() $\text {supp}(0)=\emptyset $
and that
$\text {supp}(0)=\emptyset $
and that
![]() $\emptyset < A$
and
$\emptyset < A$
and
![]() $A<\emptyset $
for every subset
$A<\emptyset $
for every subset
![]() $A\subset \mathbb {N}$
.
$A\subset \mathbb {N}$
.
Lemma 5.1 Fix
![]() $\delta>0$
and assume that
$\delta>0$
and assume that
![]() $f_{1}<\ldots <f_{d}\in W$
with
$f_{1}<\ldots <f_{d}\in W$
with
![]() $2^{-\max \text {supp}(f_{1})}\leq \frac {\delta }{2}$
are
$2^{-\max \text {supp}(f_{1})}\leq \frac {\delta }{2}$
are
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},\lambda )$
-packed for some
$(n_{j_{1}},\ldots ,n_{j_{l}},\lambda )$
-packed for some
![]() $\lambda \in \overline {\mathcal {D}}$
. Next, suppose that there exist sets of functionals
$\lambda \in \overline {\mathcal {D}}$
. Next, suppose that there exist sets of functionals
![]() $\mathcal {F}_{1},\ldots ,\mathcal {F}_{d}$
such that, for each
$\mathcal {F}_{1},\ldots ,\mathcal {F}_{d}$
such that, for each
![]() $1\leq q\leq d$
,
$1\leq q\leq d$
,
![]() $\mathcal {F}_{q}=\{g^{q}_{1},g^{q}_{2},g^{q}_{3}\}$
with
$\mathcal {F}_{q}=\{g^{q}_{1},g^{q}_{2},g^{q}_{3}\}$
with
![]() $g^{q}_{r}\in \{0\}\cup W^{\text {aux},\delta }$
, and
$g^{q}_{r}\in \{0\}\cup W^{\text {aux},\delta }$
, and
-
(1)
 $\cup _{r=1}^{3}\text {supp}(g^{q}_{r})\subset \text {supp}(f_{q})$
and
$\cup _{r=1}^{3}\text {supp}(g^{q}_{r})\subset \text {supp}(f_{q})$
and
 $\text {supp}(g^{q}_{1})<\text {supp}(g^{q}_{2})<\text {supp}(g^{q}_{3})$
,
$\text {supp}(g^{q}_{1})<\text {supp}(g^{q}_{2})<\text {supp}(g^{q}_{3})$
, -
(2) there is at most one
 $g^{q}_{\tilde {r}}\in \mathcal {F}_{q}$
such that
$g^{q}_{\tilde {r}}\in \mathcal {F}_{q}$
such that
 $g^{q}_{\tilde {r}}$
is not a unit vector,
$g^{q}_{\tilde {r}}$
is not a unit vector, -
(3) there is at most one
 $g^{q}_{r}\in \mathcal {F}_{q}$
whose support precedes the support of
$g^{q}_{r}\in \mathcal {F}_{q}$
whose support precedes the support of
 $g^{q}_{\tilde {r}}$
, and
$g^{q}_{\tilde {r}}$
, and -
(4) for
 $g^q_{\tilde r}\in \mathcal {F}_q$
that is not a unit vector,
$g^q_{\tilde r}\in \mathcal {F}_q$
that is not a unit vector,
 $\vec w(g^{q}_{\tilde {r}})=\vec w(f_{q})$
.
$\vec w(g^{q}_{\tilde {r}})=\vec w(f_{q})$
.
Then, the functionals
![]() $(g^{q}_{r})_{r=1,q=1}^{3,d}$
are
$(g^{q}_{r})_{r=1,q=1}^{3,d}$
are
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},\lambda )_{\delta }$
-packed.
$(n_{j_{1}},\ldots ,n_{j_{l}},\lambda )_{\delta }$
-packed.
Proof We proceed by induction on the length l of the tuple
![]() $(m_{j_{1}},\ldots ,m_{j_{l}})$
. Let
$(m_{j_{1}},\ldots ,m_{j_{l}})$
. Let
![]() $l=1$
and assume that
$l=1$
and assume that
![]() $f_{1}<\ldots <f_{d}\in W$
with
$f_{1}<\ldots <f_{d}\in W$
with
![]() $2^{-\max \text {supp}(f_{1})}\leq \delta $
are
$2^{-\max \text {supp}(f_{1})}\leq \delta $
are
![]() $(n_{j_{1}},\lambda )$
-packed for some
$(n_{j_{1}},\lambda )$
-packed for some
![]() $\lambda \in \overline {\mathcal {D}}$
. Then,
$\lambda \in \overline {\mathcal {D}}$
. Then,
![]() $(g^{q}_{r})_{r=1,q=1}^{3,d}\subset W^{\text {aux},\delta }_{k}$
for some
$(g^{q}_{r})_{r=1,q=1}^{3,d}\subset W^{\text {aux},\delta }_{k}$
for some
![]() $k\in \mathbb {N}$
are
$k\in \mathbb {N}$
are
![]() $S_{n_{j_{1}}}\ast \mathcal {A}_{3}$
-admissible, and we have that
$S_{n_{j_{1}}}\ast \mathcal {A}_{3}$
-admissible, and we have that
for each
![]() $g^{q}_{\tilde {r}}\in \mathcal {F}_{q}$
with at least two preceding nonzero functionals, where
$g^{q}_{\tilde {r}}\in \mathcal {F}_{q}$
with at least two preceding nonzero functionals, where
![]() $\varphi $
is the nonzero functional that is two before
$\varphi $
is the nonzero functional that is two before
![]() $g^{q}_{\tilde {r}}$
. It follows that
$g^{q}_{\tilde {r}}$
. It follows that
![]() $(g^{q}_{r})_{r=1,q=1}^{3,d}$
are skipped very fast-growing in the sense of Definition 4.1. Moreover, we have that
$(g^{q}_{r})_{r=1,q=1}^{3,d}$
are skipped very fast-growing in the sense of Definition 4.1. Moreover, we have that
for
![]() $2\leq q\leq d$
so that
$2\leq q\leq d$
so that
![]() $(g^{q}_{r})_{q=1,r=1}^{d,3}$
are
$(g^{q}_{r})_{q=1,r=1}^{d,3}$
are
![]() $(n_{j_{1}},\lambda )_{\delta }$
-packed.
$(n_{j_{1}},\lambda )_{\delta }$
-packed.
Assume now that the result holds for tuples of length l and let
![]() $f_{1}<\ldots <f_{d}\in W$
be
$f_{1}<\ldots <f_{d}\in W$
be
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},n_{j_{l+1}},\lambda )$
-packed for some
$(n_{j_{1}},\ldots ,n_{j_{l}},n_{j_{l+1}},\lambda )$
-packed for some
![]() $\lambda \in \overline {\mathcal {D}}$
. Let
$\lambda \in \overline {\mathcal {D}}$
. Let
![]() $\mathcal {F}_{1},\ldots ,\mathcal {F}_{d}$
be sets of at most three auxiliary weighted functionals as in the statement of the lemma and let
$\mathcal {F}_{1},\ldots ,\mathcal {F}_{d}$
be sets of at most three auxiliary weighted functionals as in the statement of the lemma and let
![]() $F_{1}<\ldots <F_{M}$
be a partition of
$F_{1}<\ldots <F_{M}$
be a partition of
![]() $\{1,\ldots ,d\}$
as in Definition 3.2. Note that
$\{1,\ldots ,d\}$
as in Definition 3.2. Note that
![]() $(f_{q})_{q\in F_{1}}$
are
$(f_{q})_{q\in F_{1}}$
are
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},\lambda _{1})$
-packed for some
$(n_{j_{1}},\ldots ,n_{j_{l}},\lambda _{1})$
-packed for some
![]() $\lambda _{1}\in \overline {\mathcal {D}}$
. It therefore follows from the inductive hypothesis that
$\lambda _{1}\in \overline {\mathcal {D}}$
. It therefore follows from the inductive hypothesis that
![]() $(g^{q}_{r})_{r=1,q\in F_{1}}^{3}$
are
$(g^{q}_{r})_{r=1,q\in F_{1}}^{3}$
are
![]() $(n_{j_{1}},\ldots ,n_{j_{;}},\lambda _{1})_{\delta }$
-packed. Moreover, for each
$(n_{j_{1}},\ldots ,n_{j_{;}},\lambda _{1})_{\delta }$
-packed. Moreover, for each
![]() $g^{q}_{\tilde {r}}$
with
$g^{q}_{\tilde {r}}$
with
![]() $q\in F_{p}$
for
$q\in F_{p}$
for
![]() $p>1$
, we have that
$p>1$
, we have that
 $$ \begin{align*} d(m(g^{q}_{\tilde{r}}),\lambda)&=d(m(f_{q}),\lambda) \leq d(m(f_{q}),\lambda_{p})+d(\lambda_{p},\lambda) \\ &\leq 2\cdot 2^{-\max\text{supp}(f_{\max(F_{p-1})})}\leq 2\cdot 2^{-\max\text{supp}(f_{1})}\leq \delta, \end{align*} $$
$$ \begin{align*} d(m(g^{q}_{\tilde{r}}),\lambda)&=d(m(f_{q}),\lambda) \leq d(m(f_{q}),\lambda_{p})+d(\lambda_{p},\lambda) \\ &\leq 2\cdot 2^{-\max\text{supp}(f_{\max(F_{p-1})})}\leq 2\cdot 2^{-\max\text{supp}(f_{1})}\leq \delta, \end{align*} $$
and because
![]() $(g^{q}_{r})_{q=1,r=1}^{d,3}$
are skipped very fast-growing in the sense of Definition 4.2 by the same reasoning that is used in the base case, it follows that these functionals are
$(g^{q}_{r})_{q=1,r=1}^{d,3}$
are skipped very fast-growing in the sense of Definition 4.2 by the same reasoning that is used in the base case, it follows that these functionals are
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},n_{j_{l+1}},\lambda )_{\delta }$
-packed so that the proof is complete.
$(n_{j_{1}},\ldots ,n_{j_{l}},n_{j_{l+1}},\lambda )_{\delta }$
-packed so that the proof is complete.
We now recall from [Reference Argyros and Motakis5] the notion of a rapidly increasing sequence (RIS).
Definition 5.1 Let
![]() $C\geq 1$
, let
$C\geq 1$
, let
![]() $I\subset \mathbb {N}$
be an interval, and let
$I\subset \mathbb {N}$
be an interval, and let
![]() $(j_{i})_{i\in I}$
be a strictly increasing sequence of positive integers. Then, a block sequence
$(j_{i})_{i\in I}$
be a strictly increasing sequence of positive integers. Then, a block sequence
![]() $(x_{i})_{i\in I}$
is said to be a
$(x_{i})_{i\in I}$
is said to be a
![]() $(C,(j_{i})_{i\in I})$
-RIS if the following three statements hold:
$(C,(j_{i})_{i\in I})$
-RIS if the following three statements hold:
-
(1)
 $\|x_{i}\|\leq C$
for each
$\|x_{i}\|\leq C$
for each
 $i\in \mathbb {N}$
.
$i\in \mathbb {N}$
. -
(2)
 $\max \text {supp}(x_{i-1})<\sqrt {m_{j_{i}}}$
for each
$\max \text {supp}(x_{i-1})<\sqrt {m_{j_{i}}}$
for each
 $i\in I\setminus \{\min (I)\}$
.
$i\in I\setminus \{\min (I)\}$
. -
(3)
 $|f(x_{i})|\leq \frac {C}{w(f)}$
for each
$|f(x_{i})|\leq \frac {C}{w(f)}$
for each
 $i\in I$
and for every
$i\in I$
and for every
 $f\in W$
with
$f\in W$
with
 $w(f)<m_{j_{i}}$
.
$w(f)<m_{j_{i}}$
.
We recall the steps of a standard argument that shows that there exists a RIS in every block subspace of
![]() $X_{\mathcal {D}}$
. For some of the details, we refer to specific parts of [Reference Argyros and Motakis5]. The proposition below is proved word-for-word as [Reference Argyros and Motakis5, Proposition 6.3], and it requires only two things: Theorem 3.2 (in place of [Reference Argyros and Motakis5, Proposition 4.1]) and that, for every
$X_{\mathcal {D}}$
. For some of the details, we refer to specific parts of [Reference Argyros and Motakis5]. The proposition below is proved word-for-word as [Reference Argyros and Motakis5, Proposition 6.3], and it requires only two things: Theorem 3.2 (in place of [Reference Argyros and Motakis5, Proposition 4.1]) and that, for every
![]() $C>1$
,
$C>1$
,
![]() $m_j^{-1}C^{n_j}\to \infty $
. The latter is true because, by condition (2) on page 8,
$m_j^{-1}C^{n_j}\to \infty $
. The latter is true because, by condition (2) on page 8,
 $$ \begin{align*} \log\left(\frac{C^{n_{j}}}{m_{j}}\right)>\frac{4\log(C)}{\log(100)}n_{j-1}\log(m_{j})-\log(m_{j})=\log(m_{j})\left(\frac{4\log(C)n_{j-1}}{\log(100)}-1\right). \end{align*} $$
$$ \begin{align*} \log\left(\frac{C^{n_{j}}}{m_{j}}\right)>\frac{4\log(C)}{\log(100)}n_{j-1}\log(m_{j})-\log(m_{j})=\log(m_{j})\left(\frac{4\log(C)n_{j-1}}{\log(100)}-1\right). \end{align*} $$
Proposition 5.2 Let Y be a block subspace of
![]() $X_{\mathcal {D}}$
. Then, for every
$X_{\mathcal {D}}$
. Then, for every
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $\varepsilon>0$
, and
$\varepsilon>0$
, and
![]() $\delta>0$
, there exists a
$\delta>0$
, there exists a
![]() $(n,\varepsilon )$
special convex combination
$(n,\varepsilon )$
special convex combination
![]() $x= \sum _{i=1}^mc_ix_i$
such that
$x= \sum _{i=1}^mc_ix_i$
such that
![]() $\|x\|> 1/(1+\delta )$
and
$\|x\|> 1/(1+\delta )$
and
![]() $x_1,\ldots ,x_m$
are block vectors in Y of norm at most one.
$x_1,\ldots ,x_m$
are block vectors in Y of norm at most one.
The next proposition is also proved verbatim as [Reference Argyros and Motakis5, Proposition 6.4], and it uses Remark 4.2.
Proposition 5.3 Let
![]() $j\in \mathbb {N}$
,
$j\in \mathbb {N}$
,
![]() $\varepsilon>0$
, and
$\varepsilon>0$
, and
![]() $x = \sum _{i=1}^mc_ix_i$
be an
$x = \sum _{i=1}^mc_ix_i$
be an
![]() $(n_j,\varepsilon )$
-special convex combination such that
$(n_j,\varepsilon )$
-special convex combination such that
![]() $\|x_i\|\leq 1$
,
$\|x_i\|\leq 1$
,
![]() $1\leq i\leq m$
. Then, for every
$1\leq i\leq m$
. Then, for every
![]() $f\in W$
such that
$f\in W$
such that
![]() $w(f)<m_j$
,
$w(f)<m_j$
,
 $$\begin{align*}|f(x)| \leq \frac{1+2w(f)\varepsilon}{w(f)}.\end{align*}$$
$$\begin{align*}|f(x)| \leq \frac{1+2w(f)\varepsilon}{w(f)}.\end{align*}$$
The desired conclusion follows immediately from Proposition 5.2 and Proposition 5.3.
Corollary 5.4 For every
![]() $C>1$
and in every block subspace Y of
$C>1$
and in every block subspace Y of
![]() $X_{\mathcal {D}}$
, there exists a
$X_{\mathcal {D}}$
, there exists a
![]() $(C,(j_i)_{i\in \mathbb {N}})$
-RIS
$(C,(j_i)_{i\in \mathbb {N}})$
-RIS
![]() $(x_i)$
, with
$(x_i)$
, with
![]() $\|x_i\|\geq 1$
, for
$\|x_i\|\geq 1$
, for
![]() $i\in \mathbb {N}$
.
$i\in \mathbb {N}$
.
We now prove the basic inequality that transfers the action of a weighted functional
![]() $f\in W$
to the action of auxiliary weighted functionals on appropriate unit vectors.
$f\in W$
to the action of auxiliary weighted functionals on appropriate unit vectors.
Proposition 5.5 Let
![]() $(x_{i})_{i\in I}$
be a
$(x_{i})_{i\in I}$
be a
![]() $(C,(j_{i})_{i\in I})$
-RIS with
$(C,(j_{i})_{i\in I})$
-RIS with
![]() $2^{-\min \text {supp}(x_{\min (I)})}\leq \delta $
. Then, for every functional
$2^{-\min \text {supp}(x_{\min (I)})}\leq \delta $
. Then, for every functional
![]() $f=\frac {1}{m_{j_{1}}\cdots m_{j_{l}}}\sum _{q=1}^{d}f_{q}\in W$
, there exist functionals
$f=\frac {1}{m_{j_{1}}\cdots m_{j_{l}}}\sum _{q=1}^{d}f_{q}\in W$
, there exist functionals
![]() $h\in \{0\}\cup W^{\text {aux},\delta }_{0}$
and
$h\in \{0\}\cup W^{\text {aux},\delta }_{0}$
and
![]() $g\in W^{\text {aux},\delta }$
with
$g\in W^{\text {aux},\delta }$
with
![]() $\vec w(g)=\vec w(f)$
such that
$\vec w(g)=\vec w(f)$
such that
 $$ \begin{align*} \left\vert f\left(\sum_{i\in I}a_{i}x_{i}\right)\right\vert \leq C\left(1+\frac{1}{\sqrt{m_{j_{\min(I)}}}}\right)\left\vert (h+g)\left(\sum_{i\in I}a_{i}e_{t_{i}}\right)\right\vert \end{align*} $$
$$ \begin{align*} \left\vert f\left(\sum_{i\in I}a_{i}x_{i}\right)\right\vert \leq C\left(1+\frac{1}{\sqrt{m_{j_{\min(I)}}}}\right)\left\vert (h+g)\left(\sum_{i\in I}a_{i}e_{t_{i}}\right)\right\vert \end{align*} $$
for every choice
![]() $(a_{i})_{i\in I}$
of scalars where
$(a_{i})_{i\in I}$
of scalars where
![]() $t_{i}=\max \text {supp}(x_{i})$
for each
$t_{i}=\max \text {supp}(x_{i})$
for each
![]() $i\in I$
.
$i\in I$
.
Proof We proceed by induction on the level k norming sets
![]() $W_{k}$
, and the base case is the level
$W_{k}$
, and the base case is the level
![]() $k=0$
set
$k=0$
set
![]() $W_{0}=\{\pm e_{i}^{*} \mid i\in \mathbb {N}\}$
. Indeed, if
$W_{0}=\{\pm e_{i}^{*} \mid i\in \mathbb {N}\}$
. Indeed, if
![]() $f=e^{*}_{i_{0}}\in W_{0}$
, then
$f=e^{*}_{i_{0}}\in W_{0}$
, then
 $$ \begin{align*} \left\vert e^{*}_{i_{0}}\left(\sum_{i\in I}a_{i}x_{i}\right)\right\vert \leq |a_{i_{1}}e^{*}_{i_{0}}(x_{i_{1}})| \leq C|a_{i_{1}}|= C|e^{*}_{t_{i_{1}}}(a_{t_{i_{1}}}e_{t_{i_{1}}})|, \end{align*} $$
$$ \begin{align*} \left\vert e^{*}_{i_{0}}\left(\sum_{i\in I}a_{i}x_{i}\right)\right\vert \leq |a_{i_{1}}e^{*}_{i_{0}}(x_{i_{1}})| \leq C|a_{i_{1}}|= C|e^{*}_{t_{i_{1}}}(a_{t_{i_{1}}}e_{t_{i_{1}}})|, \end{align*} $$
where
![]() $i_{0}\in \text {supp}(x_{i_{1}})$
so that the desired estimate holds with
$i_{0}\in \text {supp}(x_{i_{1}})$
so that the desired estimate holds with
![]() $h=\{0\}$
and with
$h=\{0\}$
and with
![]() $g=e^{*}_{t_{i_{1}}}$
. Note that, as part of the inductive hypothesis, we have that
$g=e^{*}_{t_{i_{1}}}$
. Note that, as part of the inductive hypothesis, we have that
![]() $\text {supp}(h),\text {supp}(g)\subset \{t_{i}\}_{i\in I}$
and that either
$\text {supp}(h),\text {supp}(g)\subset \{t_{i}\}_{i\in I}$
and that either
![]() $h=0$
or
$h=0$
or
![]() $h\in W^{\text {aux},\delta }_{0}$
,
$h\in W^{\text {aux},\delta }_{0}$
,
![]() $\text {supp}(h)<\min \text {supp}(g)$
.
$\text {supp}(h)<\min \text {supp}(g)$
.
Assume now that the desired estimate holds for functionals in the level k norming set
![]() $W_{k}$
and consider the functional
$W_{k}$
and consider the functional
 $$ \begin{align*} f=\frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{q=1}^{d}f_{q}\in W_{k+1}\setminus W_{k}, \end{align*} $$
$$ \begin{align*} f=\frac{1}{m_{j_{1}}\cdots m_{j_{l}}}\sum_{q=1}^{d}f_{q}\in W_{k+1}\setminus W_{k}, \end{align*} $$
which is to say that
![]() $f_{1}<\ldots <f_{d}$
are in
$f_{1}<\ldots <f_{d}$
are in
![]() $W_{k}$
and are
$W_{k}$
and are
![]() $(n_{j_{1}},\ldots ,n_{j_{l}},\lambda )$
-packed for some
$(n_{j_{1}},\ldots ,n_{j_{l}},\lambda )$
-packed for some
![]() $\lambda \in \overline {\mathcal {D}}$
. We omit if necessary the functionals
$\lambda \in \overline {\mathcal {D}}$
. We omit if necessary the functionals
![]() $f_{q}$
that are below the support of
$f_{q}$
that are below the support of
![]() $x_{\min (I)}$
. It then follows that
$x_{\min (I)}$
. It then follows that
and we will use this observation later. First, define the quantity
![]() $i_{0}$
by
$i_{0}$
by
if it exists. If there does exist such an
![]() $i_{0}$
, then choose
$i_{0}$
, then choose
![]() $i_{1}\in [\min (I),i_{0}]$
so that
$i_{1}\in [\min (I),i_{0}]$
so that
![]() $|a_{i_{1}}|=\max \{|a_{i}|\}_{i=\min (I)}^{i_{1}}$
and define the functional
$|a_{i_{1}}|=\max \{|a_{i}|\}_{i=\min (I)}^{i_{1}}$
and define the functional
![]() $h=\text {sign}(a_{i_{1}})e^{*}_{t_{i_{1}}}\in W^{\text {aux},\delta }_{0}$
. Note that, if
$h=\text {sign}(a_{i_{1}})e^{*}_{t_{i_{1}}}\in W^{\text {aux},\delta }_{0}$
. Note that, if
![]() $\min (I)=i_{0}=i_{1}$
, then
$\min (I)=i_{0}=i_{1}$
, then
 $$ \begin{align*} \left\vert f\left(\sum_{i\leq i_{0}}a_{i}x_{i}\right)\right\vert=|f(a_{i_{1}}x_{i_{1}})|\leq C|a_{i_{1}}|=Ch(a_{i_{1}}e_{t_{i_{1}}}), \end{align*} $$
$$ \begin{align*} \left\vert f\left(\sum_{i\leq i_{0}}a_{i}x_{i}\right)\right\vert=|f(a_{i_{1}}x_{i_{1}})|\leq C|a_{i_{1}}|=Ch(a_{i_{1}}e_{t_{i_{1}}}), \end{align*} $$
and, if
![]() $\min (I)<i_{0}$
, then
$\min (I)<i_{0}$
, then
 $$ \begin{align*} \left\vert f\left(\sum_{i\leq i_{0}}a_{i}x_{i}\right)\right\vert &\leq |a_{i_{0}}f(x_{i_{0}})|+\sum_{i<i_{0}}|a_{i}f(x_{i})| \leq C|a_{i_{0}}|+\sum_{i<i_{0}}\left\vert\frac{a_{i}}{w(f)}\sum_{q=1}^{d}f_{q}(x_{i})\right\vert \\ &\leq C|a_{i_{1}}|+\frac{|a_{i_{1}}|}{m_{j_{i_{0}}}}\sum_{i<i_{0}}\sum_{q=1}^{d}\left\vert f_{q}\left(\sum_{r\in\text{supp}(x_{i})}b_{r}e_{r}\right)\right\vert \\ &\leq C|a_{i_{1}}|+\frac{|a_{i_{1}}|}{m_{j_{i_{0}}}}\sum_{i<i_{0}}\sum_{r\in\text{supp}(x_{i})}|b_{r}| \leq C|a_{i_{1}}|+\frac{C|a_{i_{1}}|}{m_{j_{i_{0}}}}\max\text{supp}(x_{i_{0}-1}) \\ &\leq C\left(1+\frac{1}{\sqrt{m_{j_{i_{0}-1}}}}\right)|a_{i_{1}}| \leq C\left(1+\frac{1}{\sqrt{m_{j_{\min(I)}}}}\right)h\left(\sum_{i\leq i_{0}}a_{i}e_{t_{i}}\right).\end{align*} $$
$$ \begin{align*} \left\vert f\left(\sum_{i\leq i_{0}}a_{i}x_{i}\right)\right\vert &\leq |a_{i_{0}}f(x_{i_{0}})|+\sum_{i<i_{0}}|a_{i}f(x_{i})| \leq C|a_{i_{0}}|+\sum_{i<i_{0}}\left\vert\frac{a_{i}}{w(f)}\sum_{q=1}^{d}f_{q}(x_{i})\right\vert \\ &\leq C|a_{i_{1}}|+\frac{|a_{i_{1}}|}{m_{j_{i_{0}}}}\sum_{i<i_{0}}\sum_{q=1}^{d}\left\vert f_{q}\left(\sum_{r\in\text{supp}(x_{i})}b_{r}e_{r}\right)\right\vert \\ &\leq C|a_{i_{1}}|+\frac{|a_{i_{1}}|}{m_{j_{i_{0}}}}\sum_{i<i_{0}}\sum_{r\in\text{supp}(x_{i})}|b_{r}| \leq C|a_{i_{1}}|+\frac{C|a_{i_{1}}|}{m_{j_{i_{0}}}}\max\text{supp}(x_{i_{0}-1}) \\ &\leq C\left(1+\frac{1}{\sqrt{m_{j_{i_{0}-1}}}}\right)|a_{i_{1}}| \leq C\left(1+\frac{1}{\sqrt{m_{j_{\min(I)}}}}\right)h\left(\sum_{i\leq i_{0}}a_{i}e_{t_{i}}\right).\end{align*} $$
If, however, there is no such number
![]() $i_{0}$
, then the sum
$i_{0}$
, then the sum
![]() $\sum _{i\leq i_{0}}a_{i}x_{i}$
is empty, so we take
$\sum _{i\leq i_{0}}a_{i}x_{i}$
is empty, so we take
![]() $h=0$
.
$h=0$
.
Next, let
![]() $\tilde {I}=\{i\in I \mid i>i_{0}\}$
if such an
$\tilde {I}=\{i\in I \mid i>i_{0}\}$
if such an
![]() $i_{0}$
exists and put
$i_{0}$
exists and put
![]() $\tilde {I}=I$
otherwise. We then define the subsets
$\tilde {I}=I$
otherwise. We then define the subsets
 $$ \begin{align*} A&=\{ i\in\tilde{I} \mid \text{supp}(x_{i})\cap\text{supp}(f_{q})\neq\emptyset \text{ for at most one }q\} \\ I_{q}&=\{ i\in A \mid \text{supp}(x_{i})\cap\text{supp}(f_{q})\neq\emptyset\} \\ D&=\{q\mid I_{q}\neq\emptyset\} \\ B&=\tilde{I}\setminus A \end{align*} $$
$$ \begin{align*} A&=\{ i\in\tilde{I} \mid \text{supp}(x_{i})\cap\text{supp}(f_{q})\neq\emptyset \text{ for at most one }q\} \\ I_{q}&=\{ i\in A \mid \text{supp}(x_{i})\cap\text{supp}(f_{q})\neq\emptyset\} \\ D&=\{q\mid I_{q}\neq\emptyset\} \\ B&=\tilde{I}\setminus A \end{align*} $$
so that the intervals
![]() $I_{q}$
are pairwise disjoint and
$I_{q}$
are pairwise disjoint and
![]() $\text {supp}(x_{i})$
intersects the support of at least two
$\text {supp}(x_{i})$
intersects the support of at least two
![]() $f_{q}$
if
$f_{q}$
if
![]() $i\in B$
. It follows by the inductive hypothesis that, for each
$i\in B$
. It follows by the inductive hypothesis that, for each
![]() $q\in D$
, there exist functionals
$q\in D$
, there exist functionals
![]() $h_{q}\in \{0\}\cup W^{\text {aux},\delta }_{0}$
and
$h_{q}\in \{0\}\cup W^{\text {aux},\delta }_{0}$
and
![]() $g_{q}\in W^{\text {aux},\delta }$
with
$g_{q}\in W^{\text {aux},\delta }$
with
![]() $\vec w(g_{q})=\vec w(f_{q})$
so that
$\vec w(g_{q})=\vec w(f_{q})$
so that
 $$ \begin{align*} \left\vert f_{q}\left(\sum_{i\in I_{q}}a_{i}x_{i}\right)\right\vert\leq C\left(1+\frac{1}{\sqrt{m_{j_{\min(I)}}}}\right)\left\vert (h_{q}+g_{q})\left(\sum_{i\in I_{q}}a_{i}e_{t_{i}}\right)\right\vert, \end{align*} $$
$$ \begin{align*} \left\vert f_{q}\left(\sum_{i\in I_{q}}a_{i}x_{i}\right)\right\vert\leq C\left(1+\frac{1}{\sqrt{m_{j_{\min(I)}}}}\right)\left\vert (h_{q}+g_{q})\left(\sum_{i\in I_{q}}a_{i}e_{t_{i}}\right)\right\vert, \end{align*} $$
where
![]() $\text {supp}(h_{q}),\text {supp}(g_{q})\subset \text {supp}(f_{q})$
and we have that either
$\text {supp}(h_{q}),\text {supp}(g_{q})\subset \text {supp}(f_{q})$
and we have that either
![]() $h_{q}=0$
or
$h_{q}=0$
or
![]() $h_{q}\in \{e_{t_{i}}\}_{i\in I_{q}}$
and
$h_{q}\in \{e_{t_{i}}\}_{i\in I_{q}}$
and
![]() $t_{i}<\min \text {supp}(g_{q})$
. Now, replace
$t_{i}<\min \text {supp}(g_{q})$
. Now, replace
![]() $h_{q}+g_{q}$
by
$h_{q}+g_{q}$
by
![]() $\text {sign}\left [(h_{q}+g_{q})\left (\sum _{i\in I_{q}}a_{i}e_{t_{i}}\right )\right ] (h_{q}+g_{q})$
if necessary and note that
$\text {sign}\left [(h_{q}+g_{q})\left (\sum _{i\in I_{q}}a_{i}e_{t_{i}}\right )\right ] (h_{q}+g_{q})$
if necessary and note that
 $$ \begin{align*} \left\vert f\left(\sum_{i\in\tilde{I}}a_{i}x_{i}\right)\right\vert &\leq \sum_{i\in B}|f(x_{i})|+\frac{1}{w(f)}\sum_{q\in D}\left\vert f_{q}\left(\sum_{i\in I_{q}}a_{i}x_{i}\right)\right\vert \\ &\leq\frac{C}{w(f)}\sum_{i\in B}|a_{i}|+C\left(1+\frac{1}{\sqrt{m_{j_{\min(I)}}}}\right)\frac{1}{w(f)}\sum_{q\in D}(h_{q}+g_{q})\left(\sum_{i\in I_{q}}a_{i}e_{t_{i}}\right) \\ &\leq C\left(1+\frac{1}{\sqrt{m_{j_{\min(I)}}}}\right)\frac{1}{w(f)}\left[\sum_{i\in B}\tilde{h}_{i}+\sum_{q\in D}(h_{q}+g_{q}) \right]\left(\sum_{i\in\tilde{I}}a_{i}e_{t_{i}}\right),\end{align*} $$
$$ \begin{align*} \left\vert f\left(\sum_{i\in\tilde{I}}a_{i}x_{i}\right)\right\vert &\leq \sum_{i\in B}|f(x_{i})|+\frac{1}{w(f)}\sum_{q\in D}\left\vert f_{q}\left(\sum_{i\in I_{q}}a_{i}x_{i}\right)\right\vert \\ &\leq\frac{C}{w(f)}\sum_{i\in B}|a_{i}|+C\left(1+\frac{1}{\sqrt{m_{j_{\min(I)}}}}\right)\frac{1}{w(f)}\sum_{q\in D}(h_{q}+g_{q})\left(\sum_{i\in I_{q}}a_{i}e_{t_{i}}\right) \\ &\leq C\left(1+\frac{1}{\sqrt{m_{j_{\min(I)}}}}\right)\frac{1}{w(f)}\left[\sum_{i\in B}\tilde{h}_{i}+\sum_{q\in D}(h_{q}+g_{q}) \right]\left(\sum_{i\in\tilde{I}}a_{i}e_{t_{i}}\right),\end{align*} $$
where we have used the third condition from Definition 5.1 and where
![]() $\tilde {h}_{i}=\text {sign}(a_{i})e_{t_{i}}^{*}$
for each
$\tilde {h}_{i}=\text {sign}(a_{i})e_{t_{i}}^{*}$
for each
![]() $i\in B$
. It therefore follows that
$i\in B$
. It therefore follows that
 $$ \begin{align*} \left\vert f\left(\sum_{i\in I}a_{i}x_{i}\right)\right\vert \leq C\left(1+\frac{1}{\sqrt{m_{j_{\min(I)}}}}\right)\left[(h+g)\left(\sum_{i\in I}a_{i}e_{t_{i}}\right)\right], \end{align*} $$
$$ \begin{align*} \left\vert f\left(\sum_{i\in I}a_{i}x_{i}\right)\right\vert \leq C\left(1+\frac{1}{\sqrt{m_{j_{\min(I)}}}}\right)\left[(h+g)\left(\sum_{i\in I}a_{i}e_{t_{i}}\right)\right], \end{align*} $$
where either
![]() $h=0$
or
$h=0$
or
![]() $h\in \{e_{t_{i}}\}_{i=\min (I)}^{i_{0}}$
and
$h\in \{e_{t_{i}}\}_{i=\min (I)}^{i_{0}}$
and
![]() $\text {supp}(h)=t_{i_{1}}<\min \text {supp}(g)$
. Indeed, we have that
$\text {supp}(h)=t_{i_{1}}<\min \text {supp}(g)$
. Indeed, we have that
 $$ \begin{align*} g=\frac{1}{w(f)}\left(\sum_{i\in B}\tilde{h}_{i}+\sum_{q\in D}(h_{q}+g_{q})\right) \end{align*} $$
$$ \begin{align*} g=\frac{1}{w(f)}\left(\sum_{i\in B}\tilde{h}_{i}+\sum_{q\in D}(h_{q}+g_{q})\right) \end{align*} $$
so that
![]() $\vec w(f)=\vec w(g)$
. It remains to prove that
$\vec w(f)=\vec w(g)$
. It remains to prove that
![]() $g\in W^{\text {aux},\delta }$
. To that end, define for each
$g\in W^{\text {aux},\delta }$
. To that end, define for each
![]() $i\in B$
the quantity
$i\in B$
the quantity
![]() $q_{i}=\max \{1\leq q\leq d \mid \min \text {supp}(f_{q})\leq \max \text {supp}(x_{i})=t_{i}\}$
and note that the correspondence
$q_{i}=\max \{1\leq q\leq d \mid \min \text {supp}(f_{q})\leq \max \text {supp}(x_{i})=t_{i}\}$
and note that the correspondence
![]() $i\mapsto q_{i}$
is strictly increasing. If
$i\mapsto q_{i}$
is strictly increasing. If
![]() $q=q_{i}$
for some
$q=q_{i}$
for some
![]() $i\in B$
, then write
$i\in B$
, then write
![]() $\mathcal {F}_{q}=\{h_{q},g_{q},\tilde {h}_{i}\}$
. If
$\mathcal {F}_{q}=\{h_{q},g_{q},\tilde {h}_{i}\}$
. If
![]() $q\neq q_{i}$
for any
$q\neq q_{i}$
for any
![]() $i\in B$
, then write
$i\in B$
, then write
![]() $\mathcal {F}_{q}=\{h_{q},g_{q}\}$
. Note that
$\mathcal {F}_{q}=\{h_{q},g_{q}\}$
. Note that
![]() $\mathcal {F}_{q}$
may consist only of
$\mathcal {F}_{q}$
may consist only of
![]() $\tilde {h}_{i}$
or may be empty if
$\tilde {h}_{i}$
or may be empty if
![]() $q\notin D$
. It therefore follows from Lemma 5.1 (applied to
$q\notin D$
. It therefore follows from Lemma 5.1 (applied to
![]() $(f_{q})_{q\in D}$
) that
$(f_{q})_{q\in D}$
) that
![]() $g\in W^{\text {aux},\delta }$
, and this completes the proof.
$g\in W^{\text {aux},\delta }$
, and this completes the proof.
6 The failure of the Lebesgue property in subspaces of
 $X_{\mathcal {D}}$
$X_{\mathcal {D}}$
In this section, we put together the results of the previous two sections in order to prove that every subspace of
![]() $X_{\mathcal {D}}$
contains a normalized collection
$X_{\mathcal {D}}$
contains a normalized collection
![]() $(y_\lambda )_{\lambda \in \mathcal {D}}$
that satisfies the estimates (1.1), and thus witnesses the failure of the Lebesgue property.
$(y_\lambda )_{\lambda \in \mathcal {D}}$
that satisfies the estimates (1.1), and thus witnesses the failure of the Lebesgue property.
Theorem 6.1 Let Y be an infinite-dimensional block subspace of
![]() $X_{\mathcal {D}}$
. Then, there exists a normalized collection
$X_{\mathcal {D}}$
. Then, there exists a normalized collection
![]() $(y_\lambda )_{\lambda \in \mathcal {D}}$
in Y that is block with the lexicographical order of
$(y_\lambda )_{\lambda \in \mathcal {D}}$
in Y that is block with the lexicographical order of
![]() $\mathcal {D}$
such that the following holds: for every
$\mathcal {D}$
such that the following holds: for every
![]() $N\in \mathbb {N}$
and
$N\in \mathbb {N}$
and
![]() $(\mu _\lambda )_{\lambda \in \{0,1\}^N}$
in
$(\mu _\lambda )_{\lambda \in \{0,1\}^N}$
in
![]() $\mathcal {D}$
such that, for
$\mathcal {D}$
such that, for
![]() $\lambda \in \{0,1\}^N$
,
$\lambda \in \{0,1\}^N$
,
![]() $\mu _\lambda \geq \lambda $
and for any scalars
$\mu _\lambda \geq \lambda $
and for any scalars
![]() $(a_\lambda )_{\lambda \in \{0,1\}^N}$
,
$(a_\lambda )_{\lambda \in \{0,1\}^N}$
,
In particular, the Lebesgue property fails in every infinite-dimensional closed subspace of
![]() $X_{\mathcal {D}}$
.
$X_{\mathcal {D}}$
.
Proof Let
![]() $Y\subset X_{\mathcal {D}}$
and let
$Y\subset X_{\mathcal {D}}$
and let
![]() $Z\subset Y$
be a block subspace. Then, fix
$Z\subset Y$
be a block subspace. Then, fix
![]() $C> 1$
and let
$C> 1$
and let
![]() $(z_{i})$
be an infinite
$(z_{i})$
be an infinite
![]() $(C,(j_{i})_{i\in \mathbb {N}})$
-RIS in Z with
$(C,(j_{i})_{i\in \mathbb {N}})$
-RIS in Z with
![]() $1\leq \|z_{i}\|$
for each
$1\leq \|z_{i}\|$
for each
![]() $i\in \mathbb {N}$
, which exists by Corollary 5.4. By passing to a subsequence, we may assume that the conclusion of Theorem 3.2 is satisfied. Recall that the nodes of
$i\in \mathbb {N}$
, which exists by Corollary 5.4. By passing to a subsequence, we may assume that the conclusion of Theorem 3.2 is satisfied. Recall that the nodes of
![]() $\mathcal {D}$
are in lexicographical order with respect to
$\mathcal {D}$
are in lexicographical order with respect to
![]() $\mathcal {M}$
and choose for each weight
$\mathcal {M}$
and choose for each weight
![]() $m_{j}$
a number
$m_{j}$
a number
![]() $\varepsilon _{j}\in \left (0,\frac {1}{3m_{j}2^{N_{j}}}\right )$
, where
$\varepsilon _{j}\in \left (0,\frac {1}{3m_{j}2^{N_{j}}}\right )$
, where
![]() $N_j = |\phi (m_j)|$
.
$N_j = |\phi (m_j)|$
.
Now, let
![]() $F_{1}<F_{2}<\ldots $
be subsets of
$F_{1}<F_{2}<\ldots $
be subsets of
![]() $\mathbb {N}$
so that
$\mathbb {N}$
so that
![]() $\{\min \text {supp}(z_{i}) \mid i\in F_{j}\}$
is a maximal set in
$\{\min \text {supp}(z_{i}) \mid i\in F_{j}\}$
is a maximal set in
![]() $S_{n_{j}}$
with respect to inclusion for each
$S_{n_{j}}$
with respect to inclusion for each
![]() $j\in \mathbb {N}$
. It follows from Proposition 2.1 that there exist coefficients
$j\in \mathbb {N}$
. It follows from Proposition 2.1 that there exist coefficients
![]() $(c^{j}_{i})_{i\in F_{j}}$
so that the vector
$(c^{j}_{i})_{i\in F_{j}}$
so that the vector
![]() $\sum _{i\in F_{j}}c^{j}_{i}e_{i}$
is an
$\sum _{i\in F_{j}}c^{j}_{i}e_{i}$
is an
![]() $(n_{j},\frac {\varepsilon _{j}}{2})$
-basic scc. In particular, we have that
$(n_{j},\frac {\varepsilon _{j}}{2})$
-basic scc. In particular, we have that
![]() $x_{m_j}=\sum _{i\in F_{j}}c^{j}_{i}z_{i}$
is an
$x_{m_j}=\sum _{i\in F_{j}}c^{j}_{i}z_{i}$
is an
![]() $(n_{j},\frac {\varepsilon _{j}}{2})$
-scc, and we note also that
$(n_{j},\frac {\varepsilon _{j}}{2})$
-scc, and we note also that
 $$ \begin{align*} \|x_{m_j}\|=\left\Vert\sum_{i\in F_{j}}c^{j}_{i}z_{i}\right\Vert \geq \frac{m_{1}-1}{m_{1}m_{j}}\sum_{i\in F_{j}}c^{j}_{i}=\frac{m_{1}-1}{m_{1}m_{j}}\end{align*} $$
$$ \begin{align*} \|x_{m_j}\|=\left\Vert\sum_{i\in F_{j}}c^{j}_{i}z_{i}\right\Vert \geq \frac{m_{1}-1}{m_{1}m_{j}}\sum_{i\in F_{j}}c^{j}_{i}=\frac{m_{1}-1}{m_{1}m_{j}}\end{align*} $$
from Theorem 3.2. Let
![]() $\tilde {x}_{m_j}=m_{j}x_{j}$
and define, for
$\tilde {x}_{m_j}=m_{j}x_{j}$
and define, for
![]() $\lambda \in \mathcal {D}$
,
$\lambda \in \mathcal {D}$
,
![]() $y_{\lambda }= \tilde x_{\phi ^{-1}(m_j)}/\|\tilde x_{\phi ^{-1}(m_j)}\|$
so that
$y_{\lambda }= \tilde x_{\phi ^{-1}(m_j)}/\|\tilde x_{\phi ^{-1}(m_j)}\|$
so that
![]() $(y_{\lambda })$
is a normalized sequence in Z that is block in the lexicographical order of
$(y_{\lambda })$
is a normalized sequence in Z that is block in the lexicographical order of
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
Now, fix
![]() $N\in \mathbb {N}$
and, for
$N\in \mathbb {N}$
and, for
![]() $\lambda \in \{0,1\}^N$
, let
$\lambda \in \{0,1\}^N$
, let
![]() $\mu _\lambda \in \mathcal {D}$
such that
$\mu _\lambda \in \mathcal {D}$
such that
![]() $\mu _\lambda \geq \lambda $
. Because
$\mu _\lambda \geq \lambda $
. Because
![]() $(y_\lambda )_{\lambda \in \mathcal {D}}$
is lexicographically block, there are
$(y_\lambda )_{\lambda \in \mathcal {D}}$
is lexicographically block, there are
![]() $2^N\leq j_1<\cdots <j_{2^N}$
such that
$2^N\leq j_1<\cdots <j_{2^N}$
such that
![]() $\phi (\{m_{j_1},\ldots ,m_{j_{2^N}}\}) = \{\mu _\lambda :\lambda \in \{0,1\}^N\}$
. In particular,
$\phi (\{m_{j_1},\ldots ,m_{j_{2^N}}\}) = \{\mu _\lambda :\lambda \in \{0,1\}^N\}$
. In particular,
![]() $\min \text {supp}(y_{\mu _\lambda })\geq N$
,
$\min \text {supp}(y_{\mu _\lambda })\geq N$
,
![]() $\lambda \in \{0,1\}^N$
. Furthermore, for
$\lambda \in \{0,1\}^N$
. Furthermore, for
![]() $\lambda \in \{0,1\}^N$
,
$\lambda \in \{0,1\}^N$
,
![]() $\mu _\lambda \geq \lambda $
, and thus, for
$\mu _\lambda \geq \lambda $
, and thus, for
![]() $1\leq k\neq k'\leq 2^N$
,
$1\leq k\neq k'\leq 2^N$
,
![]() $d(m_{j_k},m_{j_{k'}}) \geq 2^{-N}$
. Then, it follows that
$d(m_{j_k},m_{j_{k'}}) \geq 2^{-N}$
. Then, it follows that
 $$ \begin{align*} \left\Vert \sum_{\lambda\in\{0,1\}^N}y_{\mu_\lambda}\right\Vert =\mathscr{F}\left(\sum_{\lambda\in\{0,1\}^N}y_{\mu_\lambda}\right) =\mathscr{F}\left(\sum_{k=0}^{2^{N}-1}\frac{1}{\|\tilde{x}_{m_{j_{k}}}\|}m_{j_{k}}\sum_{i\in F_{j_{k}}}c^{j_{k}}_{i}z_{i}\right) \qquad (\#) \end{align*} $$
$$ \begin{align*} \left\Vert \sum_{\lambda\in\{0,1\}^N}y_{\mu_\lambda}\right\Vert =\mathscr{F}\left(\sum_{\lambda\in\{0,1\}^N}y_{\mu_\lambda}\right) =\mathscr{F}\left(\sum_{k=0}^{2^{N}-1}\frac{1}{\|\tilde{x}_{m_{j_{k}}}\|}m_{j_{k}}\sum_{i\in F_{j_{k}}}c^{j_{k}}_{i}z_{i}\right) \qquad (\#) \end{align*} $$
for some norming functional
![]() $\mathscr {F}\in W$
, and, by Proposition 5.5, this quantity is bounded above by
$\mathscr {F}\in W$
, and, by Proposition 5.5, this quantity is bounded above by
 $$ \begin{align*} C\left\vert (h+g)\left(\sum_{k=0}^{2^{N}-1}\frac{1}{\|\tilde{x}_{m_{j_{k}}}\|}m_{j_{k}}\sum_{i\in F_{j_{k}}}c^{j_{k}}_{i}e_{\rho(i)}\right)\right\vert \qquad (\#\#), \end{align*} $$
$$ \begin{align*} C\left\vert (h+g)\left(\sum_{k=0}^{2^{N}-1}\frac{1}{\|\tilde{x}_{m_{j_{k}}}\|}m_{j_{k}}\sum_{i\in F_{j_{k}}}c^{j_{k}}_{i}e_{\rho(i)}\right)\right\vert \qquad (\#\#), \end{align*} $$
where
![]() $h\in W^{\text {aux},\delta }_{0}\cup \{0\}$
,
$h\in W^{\text {aux},\delta }_{0}\cup \{0\}$
,
![]() $g\in W^{\text {aux},\delta }$
with
$g\in W^{\text {aux},\delta }$
with
![]() $\vec w(g)=\vec w(\mathscr {F})$
, and where
$\vec w(g)=\vec w(\mathscr {F})$
, and where
![]() $\rho (i)=\max \text {supp}(z_{i})$
for each
$\rho (i)=\max \text {supp}(z_{i})$
for each
![]() $i\in \mathbb {N}$
. Note that
$i\in \mathbb {N}$
. Note that
![]() $\sum _{i\in F_{j_{k}}}c^{j_{k}}_{i}e_{\rho (i)}$
is for each
$\sum _{i\in F_{j_{k}}}c^{j_{k}}_{i}e_{\rho (i)}$
is for each
![]() $0\leq k\leq 2^{N}-1$
an
$0\leq k\leq 2^{N}-1$
an
![]() $(n_{j_{k}},\varepsilon _{j_{k}})$
-basic scc by the observation that immediately follows Proposition 2.1, and note also that
$(n_{j_{k}},\varepsilon _{j_{k}})$
-basic scc by the observation that immediately follows Proposition 2.1, and note also that
 $$\begin{align*}\frac{m_{j_{k}}}{\|\tilde{x}_{m_{j_{k}}}\|}=\frac{1}{\|x_{m_{j_{k}}}\|}\leq \frac{m_{1}m_{j_{k}}}{m_{1}-1}.\end{align*}$$
$$\begin{align*}\frac{m_{j_{k}}}{\|\tilde{x}_{m_{j_{k}}}\|}=\frac{1}{\|x_{m_{j_{k}}}\|}\leq \frac{m_{1}m_{j_{k}}}{m_{1}-1}.\end{align*}$$
It therefore follows that
![]() $(\#\#)$
is bounded above by
$(\#\#)$
is bounded above by
 $$ \begin{align*} C\max_{0\leq k\leq 2^{N}-1}\frac{m_{j_{k}}\varepsilon_{j_{k}}}{\|\tilde{x}_{j_{k}}\|} +C\left\vert g\left(\sum_{k=0}^{2^{N}-1}\frac{1}{\|\tilde{x}_{j_{k}}\|}m_{j_{k}}\sum_{i\in F_{j_{k}}}c^{j_{k}}_{i}e_{\rho(i)}\right)\right\vert \qquad (\#\#\#), \end{align*} $$
$$ \begin{align*} C\max_{0\leq k\leq 2^{N}-1}\frac{m_{j_{k}}\varepsilon_{j_{k}}}{\|\tilde{x}_{j_{k}}\|} +C\left\vert g\left(\sum_{k=0}^{2^{N}-1}\frac{1}{\|\tilde{x}_{j_{k}}\|}m_{j_{k}}\sum_{i\in F_{j_{k}}}c^{j_{k}}_{i}e_{\rho(i)}\right)\right\vert \qquad (\#\#\#), \end{align*} $$
and lastly, by Proposition 4.3, we note that
![]() $(\#\#\#)$
is bounded above by
$(\#\#\#)$
is bounded above by
 $$ \begin{align*} C\frac{m_{1}m_{j_{k}}}{m_{1}-1}\frac{1}{3m_{j_{k}} 2^{N_{j_{k}}}}+C\left(1+\frac{4}{\sqrt{w(g)}}\right)\max_{0\leq k\leq 2^{N}-1}\frac{1}{\|\tilde{x}_{j_{k}}\|} \leq C\frac{100}{99}\left(1+\left(1+\frac{2}{5}\right)\right)\leq 3, \end{align*} $$
$$ \begin{align*} C\frac{m_{1}m_{j_{k}}}{m_{1}-1}\frac{1}{3m_{j_{k}} 2^{N_{j_{k}}}}+C\left(1+\frac{4}{\sqrt{w(g)}}\right)\max_{0\leq k\leq 2^{N}-1}\frac{1}{\|\tilde{x}_{j_{k}}\|} \leq C\frac{100}{99}\left(1+\left(1+\frac{2}{5}\right)\right)\leq 3, \end{align*} $$
for
![]() $C>1$
sufficiently close to one. The estimate for arbitrary scalars coefficients follows from the 1-unconditionality of the basis of
$C>1$
sufficiently close to one. The estimate for arbitrary scalars coefficients follows from the 1-unconditionality of the basis of
![]() $X_{\mathcal {D}}$
.
$X_{\mathcal {D}}$
.