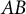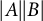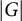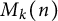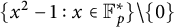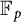1 Introduction
Let q be a prime power, and let
![]() ${\mathbb F}_q$
be the finite field with q elements. Let G be a multiplicative subgroup of
${\mathbb F}_q$
be the finite field with q elements. Let G be a multiplicative subgroup of
![]() ${\mathbb F}_q$
. While G itself has a “perfect” multiplicative structure, it is natural to ask if a (non-trivial additive) shift of G still possesses some multiplicative structure. Indeed, as a fundamental question in additive combinatorics, this question has drawn the attention of many researchers and it is closely related to many questions in number theory. For example, a classical result of Vinogradov [Reference Vinogradov36] states that for a prime p and an integer n such that
${\mathbb F}_q$
. While G itself has a “perfect” multiplicative structure, it is natural to ask if a (non-trivial additive) shift of G still possesses some multiplicative structure. Indeed, as a fundamental question in additive combinatorics, this question has drawn the attention of many researchers and it is closely related to many questions in number theory. For example, a classical result of Vinogradov [Reference Vinogradov36] states that for a prime p and an integer n such that
![]() $p \nmid n$
, if
$p \nmid n$
, if
![]() $A, B \subset \{1,2,\ldots , p-1\}$
, then
$A, B \subset \{1,2,\ldots , p-1\}$
, then
 $$ \begin{align} \bigg|\sum_{a\in A,\, b\in B} \bigg(\frac{ab+n}{p}\bigg)\bigg| \leq \sqrt{p|A||B|}. \end{align} $$
$$ \begin{align} \bigg|\sum_{a\in A,\, b\in B} \bigg(\frac{ab+n}{p}\bigg)\bigg| \leq \sqrt{p|A||B|}. \end{align} $$
More generally, inequality (1.1) extends to all nontrivial multiplicative characters over all finite fields; see Proposition 3.1. Inequality (1.1) leads an estimate on the size of a product set contains in the set of shifted squares: if
![]() $A,B \subset {\mathbb F}_p^*$
,
$A,B \subset {\mathbb F}_p^*$
,
![]() $\lambda \in {\mathbb F}_p^*$
, and G is the subgroup of
$\lambda \in {\mathbb F}_p^*$
, and G is the subgroup of
![]() ${\mathbb F}_p^*$
of index
${\mathbb F}_p^*$
of index
![]() $2$
such that
$2$
such that
![]() $AB \subset (G+\lambda )$
, then
$AB \subset (G+\lambda )$
, then
For more recent works related to this question and its connection with other problems, we refer to [Reference Gyarmati17, Reference Macourt, Shkredov and Shparlinski27, Reference Sárközy31, Reference Vyugin and Shkredov37] and references therein. An analog of this question over integers is closely related to the well-studied Diophantine tuples and their generalizations; see Section 1.1.
In this article, we study the multiplicative structure of a shifted multiplicative subgroup following the spirit of the aforementioned works and discuss a few new applications in additive combinatorics and Diophantine equations. More precisely, one of our contributions is the following theorem.
Theorem 1.1 Let
![]() $d \mid (q-1)$
with
$d \mid (q-1)$
with
![]() $d \ge 2$
. Let
$d \ge 2$
. Let
![]() $S_d=\{x^d: x \in {\mathbb F}_q^*\}$
. Let
$S_d=\{x^d: x \in {\mathbb F}_q^*\}$
. Let
![]() $A,B \subset {\mathbb F}_q^*$
and
$A,B \subset {\mathbb F}_q^*$
and
![]() $\lambda \in {\mathbb F}_q^*$
with
$\lambda \in {\mathbb F}_q^*$
with
![]() $|A|, |B| \geq 2$
. Assume further that
$|A|, |B| \geq 2$
. Assume further that
![]() $\binom {|A|-1+\frac {q-1}{d}}{|A|} \not \equiv 0 \ \pmod p$
if
$\binom {|A|-1+\frac {q-1}{d}}{|A|} \not \equiv 0 \ \pmod p$
if
![]() $q \neq p$
. If
$q \neq p$
. If
![]() $AB+\lambda \subset S_d \cup \{0\}$
, then
$AB+\lambda \subset S_d \cup \{0\}$
, then
Moreover, when
![]() $\lambda \in S_d$
, we have a stronger upper bound:
$\lambda \in S_d$
, we have a stronger upper bound:
Clearly, Theorem 1.1 improves inequality (1.2) implied by Vinogradov’s estimate (1.1) when
![]() $d=2$
, and the generalization of inequality (1.2) by Gyarmati [Reference Gyarmati17, Theorem 8] for general d, where the upper bound is given by
$d=2$
, and the generalization of inequality (1.2) by Gyarmati [Reference Gyarmati17, Theorem 8] for general d, where the upper bound is given by
![]() $(\sqrt {p}+2)^2$
when
$(\sqrt {p}+2)^2$
when
![]() $q=p$
is a prime. We remark that in general the condition on the binomial coefficient in the statement of Theorem 1.1 cannot be dropped when q is not a prime; see Theorem 1.6.
$q=p$
is a prime. We remark that in general the condition on the binomial coefficient in the statement of Theorem 1.1 cannot be dropped when q is not a prime; see Theorem 1.6.
The proof of Theorem 1.1 is based on Stepanov’s method [Reference Stepanov35], and is motivated by a recent breakthrough of Hanson and Petridis [Reference Hanson and Petridis21]. In fact, Theorem 1.1 can be viewed as a multiplicative analog of their results. Going beyond the perspective of these multiplicative analogs, we provide new insights into the application of Stepanov’s method. For example, our technique applies to all finite fields while their technique only works over prime fields. We also prove a similar result for restricted product sets (see Theorem 4.2), whereas their technique appears to only lead to a weaker bound; see Remark 4.3.
Besides Theorem 1.1, we also provide three novel applications of Theorem 1.1 and its variants. These applications significantly improve on many previous results in the literature. Unsurprisingly, to achieve these applications, we need additional tools and insights from Diophantine approximation, sieve methods, additive combinatorics, and character sums. From here, we briefly mention what applications are about. In Section 1.1, we improve the upper bound of generalized Diophantine tuples over integers. Interestingly, Theorem 1.1 is closely related to a bipartite version of Diophantine tuples over finite fields. This new perspective yields a substantial improvement in the result of generalized Diophantine tuples over integers. In Section 1.2, we obtain the first nontrivial upper bounds on generalized Diophantine tuples and strong Diophantine tuples over finite fields. Moreover, some of our new bounds are sharp. Last but not least, in Section 1.3, we make significant progress toward a conjecture of Sárközy [Reference Sárközy31] on multiplicative decompositions of shifted multiplicative subgroups. We elaborate on the context of these applications in the next subsections.
1.1 Diophantine tuples over integers
A set
![]() $\{a_{1}, a_{2},\ldots , a_{m}\}$
of distinct positive integers is a Diophantine m-tuple if the product of any two distinct elements in the set is one less than a square. The first known example of integral Diophantine
$\{a_{1}, a_{2},\ldots , a_{m}\}$
of distinct positive integers is a Diophantine m-tuple if the product of any two distinct elements in the set is one less than a square. The first known example of integral Diophantine
![]() $4$
-tuples is
$4$
-tuples is
![]() $\{1,3,8,120\}$
which was studied by Fermat. The Diophantine
$\{1,3,8,120\}$
which was studied by Fermat. The Diophantine
![]() $4$
-tuple was extended by Euler to the rational
$4$
-tuple was extended by Euler to the rational
![]() $5$
-tuple
$5$
-tuple
![]() $\{1, 3, 8, 120, \frac {777480}{8288641}\}$
, and it had been conjectured that there is no Diophantine
$\{1, 3, 8, 120, \frac {777480}{8288641}\}$
, and it had been conjectured that there is no Diophantine
![]() $5$
-tuple. The difficulty of extending Diophantine tuples can be explained by its connection to the problem of finding integral points on elliptic curves: if
$5$
-tuple. The difficulty of extending Diophantine tuples can be explained by its connection to the problem of finding integral points on elliptic curves: if
![]() $\{a,b,c\}$
forms a Diophantine
$\{a,b,c\}$
forms a Diophantine
![]() $3$
-tuple, in order to find a positive integer d such that
$3$
-tuple, in order to find a positive integer d such that
![]() $\{a,b,c,d\}$
is a Diophantine
$\{a,b,c,d\}$
is a Diophantine
![]() $4$
-tuple, we need to solve the following simultaneous equation for d:
$4$
-tuple, we need to solve the following simultaneous equation for d:
This is related to the problem of finding an integral point
![]() $(d,str)$
on the following elliptic curve
$(d,str)$
on the following elliptic curve
From this, we can deduce that there are no infinite Diophantine m-tuples by Siegel’s theorem on integral points. On the other hand, Siegel’s theorem is not sufficient to give an upper bound on the size of Diophantine tuples due to its ineffectivity. In the same vein, finding a Diophantine tuple of size greater than or equal to
![]() $5$
is related to the problem of finding integral points on hyperelliptic curves of genus
$5$
is related to the problem of finding integral points on hyperelliptic curves of genus
![]() $g\geq 2$
. Despite the aforementioned difficulties, the conjecture on the non-existence of Diophantine
$g\geq 2$
. Despite the aforementioned difficulties, the conjecture on the non-existence of Diophantine
![]() $5$
-tuples was recently proved to be true in the sequel of important papers by Dujella [Reference Dujella9], and He, Togbé, and Ziegler [Reference He, Togbé and Ziegler22].
$5$
-tuples was recently proved to be true in the sequel of important papers by Dujella [Reference Dujella9], and He, Togbé, and Ziegler [Reference He, Togbé and Ziegler22].
The definition of Diophantine m-tuples has been generalized and studied in various contexts. We refer to the recent book of Dujella [Reference Dujella10] for a thorough list of known results on the topic and their reference. In this article, we focus on the following generalization of Diophantine tuples: for each
![]() $n \ge 1$
and
$n \ge 1$
and
![]() $k \ge 2$
, we call a set
$k \ge 2$
, we call a set
![]() $\{a_{1},a_{2},\ldots , a_{m}\}$
of distinct positive integers a Diophantine m-tuple with property
$\{a_{1},a_{2},\ldots , a_{m}\}$
of distinct positive integers a Diophantine m-tuple with property
![]() $D_{k}(n)$
if the product of any two distinct elements is n less than a kth power. We write
$D_{k}(n)$
if the product of any two distinct elements is n less than a kth power. We write
Similar to the classical case, the problem of finding
![]() $M_{k}(n)$
for
$M_{k}(n)$
for
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $n \geq 1$
is related to the problem of counting the number of integral points of the superelliptic curve
$n \geq 1$
is related to the problem of counting the number of integral points of the superelliptic curve
The theorem of Faltings [Reference Faltings13] guarantees that the above curve has only finitely many integral points, and this, in turn, implies that a set with property
![]() $D_k(n)$
must be finite. The known upper bounds for the number of integral points depend on the coefficients of
$D_k(n)$
must be finite. The known upper bounds for the number of integral points depend on the coefficients of
![]() $f(x)$
. The Caporaso–Harris–Mazur conjecture [Reference Caporaso, Harris and Mazur6] implies that
$f(x)$
. The Caporaso–Harris–Mazur conjecture [Reference Caporaso, Harris and Mazur6] implies that
![]() $M_k(n)$
is uniformly bounded, independent of n. For other conditional bounds, we refer the readers to Section 2.4.
$M_k(n)$
is uniformly bounded, independent of n. For other conditional bounds, we refer the readers to Section 2.4.
Unconditionally, in [Reference Bugeaud and Dujella4], Bugeaud and Dujella [Reference Bugeaud and Dujella4, Corollary 4] showed that
![]() ${M_3(1) \leq 7}$
,
${M_3(1) \leq 7}$
,
![]() $M_k(1) \leq 5$
for
$M_k(1) \leq 5$
for
![]() $k \in \{4,5\}$
,
$k \in \{4,5\}$
,
![]() $M_k(1) \leq 4$
for
$M_k(1) \leq 4$
for
![]() $6 \leq k \leq 176$
, and the uniform bound
$6 \leq k \leq 176$
, and the uniform bound
![]() $M_{k}(1) \leq 3$
for any
$M_{k}(1) \leq 3$
for any
![]() $k \geq 177$
Footnote
1
. On the other hand, the best-known upper bound on
$k \geq 177$
Footnote
1
. On the other hand, the best-known upper bound on
![]() $M_2(n)$
is
$M_2(n)$
is
![]() $(2+o(1))\log n$
, due to the second author [Reference Yip39]. Very recently, Dixit, Murty, and the first author [Reference Dixit, Kim and Murty7] studied the size of a generalized Diophantine m-tuple with property
$(2+o(1))\log n$
, due to the second author [Reference Yip39]. Very recently, Dixit, Murty, and the first author [Reference Dixit, Kim and Murty7] studied the size of a generalized Diophantine m-tuple with property
![]() $D_k(n)$
, improving the previously best-known upper bound
$D_k(n)$
, improving the previously best-known upper bound
![]() $M_3(n)\leq 2|n|^{17}+6$
and
$M_3(n)\leq 2|n|^{17}+6$
and
![]() $M_k(n) \leq 2|n|^5 + 3$
for
$M_k(n) \leq 2|n|^5 + 3$
for
![]() $k\geq 5$
given by Bérczes, Dujella, Hajdu, and Luca [Reference Bérczes, Dujella, Hajdu and Luca2] when
$k\geq 5$
given by Bérczes, Dujella, Hajdu, and Luca [Reference Bérczes, Dujella, Hajdu and Luca2] when
![]() $n \to \infty $
. They showed that if k is fixed and
$n \to \infty $
. They showed that if k is fixed and
![]() $n \to \infty $
, then
$n \to \infty $
, then
![]() $M_k(n)\ll _k \log n$
. Following their proof in [Reference Dixit, Kim and Murty7], the bound can be more explicitly expressed as
$M_k(n)\ll _k \log n$
. Following their proof in [Reference Dixit, Kim and Murty7], the bound can be more explicitly expressed as
![]() $M_k(n)\leq (3\phi (k)+o(1))\log n$
when
$M_k(n)\leq (3\phi (k)+o(1))\log n$
when
![]() $k \geq 3$
is fixed,
$k \geq 3$
is fixed,
![]() $n \to \infty $
, and
$n \to \infty $
, and
![]() $\phi $
is the Euler phi function. Note that their upper bound on
$\phi $
is the Euler phi function. Note that their upper bound on
![]() $M_k(n)$
is perhaps not desirable. Indeed, it is natural to expect that
$M_k(n)$
is perhaps not desirable. Indeed, it is natural to expect that
![]() $M_k(n)$
would decrease if n is fixed, and k increases, since kth powers become sparser. Instead, our new upper bounds on
$M_k(n)$
would decrease if n is fixed, and k increases, since kth powers become sparser. Instead, our new upper bounds on
![]() $M_k(n)$
support this heuristic.
$M_k(n)$
support this heuristic.
In this article, we provide a significant improvement on the upper bound of
![]() $M_{k}(n)$
by using a novel combination of Stepanov’s method and Gallagher’s larger sieve inequality. In order to state our first result, we define the following constant
$M_{k}(n)$
by using a novel combination of Stepanov’s method and Gallagher’s larger sieve inequality. In order to state our first result, we define the following constant
 $$ \begin{align} \eta_k=\min_{\mathcal{I}} \frac{|\mathcal{I}|}{T_{\mathcal{I}}^2} \end{align} $$
$$ \begin{align} \eta_k=\min_{\mathcal{I}} \frac{|\mathcal{I}|}{T_{\mathcal{I}}^2} \end{align} $$
for each
![]() $k \geq 2$
, where the minimum is taken over all nonempty subsets
$k \geq 2$
, where the minimum is taken over all nonempty subsets
![]() $\mathcal {I}$
of the set
$\mathcal {I}$
of the set
and
![]() $T_{\mathcal {I}}=\sum _{i \in \mathcal {I}} \sqrt {\gcd (i-1,k)}$
.
$T_{\mathcal {I}}=\sum _{i \in \mathcal {I}} \sqrt {\gcd (i-1,k)}$
.
Theorem 1.2 There is a constant
![]() $c'>0$
, such that as
$c'>0$
, such that as
![]() $n \to \infty $
,
$n \to \infty $
,
 $$ \begin{align} M_k(n)\leq \bigg(\frac{2k}{k-2}+o(1)\bigg) \ \eta_k \phi(k) \log n, \end{align} $$
$$ \begin{align} M_k(n)\leq \bigg(\frac{2k}{k-2}+o(1)\bigg) \ \eta_k \phi(k) \log n, \end{align} $$
holds uniformly for positive integers
![]() $k,n \geq 3$
such that
$k,n \geq 3$
such that
![]() $\log k \leq c'\sqrt {\log \log n}$
.
$\log k \leq c'\sqrt {\log \log n}$
.
The constant
![]() $\eta _k$
is essentially computed via the optimal collection of “admissible” residue classes when applying Gallagher’s larger sieve (see Section 5). Note that when
$\eta _k$
is essentially computed via the optimal collection of “admissible” residue classes when applying Gallagher’s larger sieve (see Section 5). Note that when
![]() $\mathcal {I}=\{1\}$
, we have
$\mathcal {I}=\{1\}$
, we have
![]() $T_{\mathcal {I}}=\sqrt {k}$
, and hence we have
$T_{\mathcal {I}}=\sqrt {k}$
, and hence we have
![]() $\eta _k \leq \frac {1}{k}$
. In particular, if
$\eta _k \leq \frac {1}{k}$
. In particular, if
![]() $k \geq 3$
is fixed and
$k \geq 3$
is fixed and
![]() $n \to \infty $
, inequality (1.4) implies the upper bound
$n \to \infty $
, inequality (1.4) implies the upper bound
which already improves the best-known upper bound
![]() $M_k(n)\leq (3\phi (k)+o(1))\log n$
of [Reference Dixit, Kim and Murty7] that we mentioned earlier substantially. In Appendix A, we illustrate the bound in inequality (1.4): for
$M_k(n)\leq (3\phi (k)+o(1))\log n$
of [Reference Dixit, Kim and Murty7] that we mentioned earlier substantially. In Appendix A, we illustrate the bound in inequality (1.4): for
![]() $2 \leq k \leq 1001$
, we compute the suggested upper bound
$2 \leq k \leq 1001$
, we compute the suggested upper bound
of
![]() $\gamma _{k}=\limsup _{n \to \infty } \frac {M_k(n)}{\log n}$
. From Figure A.1, one can compare the bound of
$\gamma _{k}=\limsup _{n \to \infty } \frac {M_k(n)}{\log n}$
. From Figure A.1, one can compare the bound of
![]() $M_{k}(n)$
in Theorem 1.2 with the bound in [Reference Dixit, Kim and Murty7]. From inequality (1.5), we see
$M_{k}(n)$
in Theorem 1.2 with the bound in [Reference Dixit, Kim and Murty7]. From inequality (1.5), we see
![]() $\gamma _k$
is uniformly bounded by
$\gamma _k$
is uniformly bounded by
![]() $6$
. Table A.2 illustrates better upper bounds on
$6$
. Table A.2 illustrates better upper bounds on
![]() $\gamma _k$
for
$\gamma _k$
for
![]() $2 \le k \leq 201$
. In particular, we use a simple greedy algorithm to determine
$2 \le k \leq 201$
. In particular, we use a simple greedy algorithm to determine
![]() $\eta _k$
for a fixed k. We also refer to Section 5.3 for a simple upper bound on
$\eta _k$
for a fixed k. We also refer to Section 5.3 for a simple upper bound on
![]() $\eta _k$
, which well approximates
$\eta _k$
, which well approximates
![]() $\eta _k$
empirically.
$\eta _k$
empirically.
At first glance, Theorem 1.2 improves the bound in [Reference Dixit, Kim and Murty7] of
![]() $M_k(n)$
by only a constant multiplicative factor when k is fixed. Nevertheless, note that Theorem 1.2 holds uniformly for k and n as long as
$M_k(n)$
by only a constant multiplicative factor when k is fixed. Nevertheless, note that Theorem 1.2 holds uniformly for k and n as long as
![]() $\log k \leq c'\sqrt {\log \log n}$
. Thus, when k is assumed to be a function of n which increases as n increases, we can break the “
$\log k \leq c'\sqrt {\log \log n}$
. Thus, when k is assumed to be a function of n which increases as n increases, we can break the “
![]() $\log n$
barrier” in [Reference Dixit, Kim and Murty7], that is,
$\log n$
barrier” in [Reference Dixit, Kim and Murty7], that is,
![]() $M_{k}(n)=O_{k}(\log n)$
, and provide a dramatic improvement.
$M_{k}(n)=O_{k}(\log n)$
, and provide a dramatic improvement.
Theorem 1.3 There is
![]() $k=k(n)$
such that
$k=k(n)$
such that
![]() $\log k \asymp \sqrt {\log \log n}$
, and
$\log k \asymp \sqrt {\log \log n}$
, and
 $$ \begin{align*}M_k(n)\ll \exp\bigg({-}\frac{c"(\log \log n)^{1/4}}{\log \log \log n}\bigg) \log n, \end{align*} $$
$$ \begin{align*}M_k(n)\ll \exp\bigg({-}\frac{c"(\log \log n)^{1/4}}{\log \log \log n}\bigg) \log n, \end{align*} $$
where
![]() $c">0$
is an absolute constant.
$c">0$
is an absolute constant.
The proofs of Theorems 1.2 and 1.3 require the study of (generalized) Diophantine tuples over finite fields, which we discuss below.
1.2 Diophantine tuples over finite fields
A Diophantine m-tuple with property
![]() $D_{d}(\lambda ,\mathbb {F}_{q})$
is a set
$D_{d}(\lambda ,\mathbb {F}_{q})$
is a set
![]() $\{a_1,\ldots , a_m\}$
of m distinct elements in
$\{a_1,\ldots , a_m\}$
of m distinct elements in
![]() $\mathbb {F}_{q}^{*}$
such that
$\mathbb {F}_{q}^{*}$
such that
![]() $a_{i}a_{j}+\lambda $
is a dth power in
$a_{i}a_{j}+\lambda $
is a dth power in
![]() $\mathbb {F}_q^*$
or
$\mathbb {F}_q^*$
or
![]() $0$
whenever
$0$
whenever
![]() $i\neq j$
. Moreover, we also define the strong Diophantine tuples in finite fields motivated by Dujella and Petričević [Reference Dujella and Petričević11]: a strong Diophantine m-tuple with property
$i\neq j$
. Moreover, we also define the strong Diophantine tuples in finite fields motivated by Dujella and Petričević [Reference Dujella and Petričević11]: a strong Diophantine m-tuple with property
![]() $SD_{d}(\lambda ,\mathbb {F}_q)$
is a set
$SD_{d}(\lambda ,\mathbb {F}_q)$
is a set
![]() $\{a_1,\ldots , a_m\}$
of m distinct elements in
$\{a_1,\ldots , a_m\}$
of m distinct elements in
![]() $\mathbb {F}_{q}^{*}$
such that
$\mathbb {F}_{q}^{*}$
such that
![]() $a_{i}a_{j}+\lambda $
is a dth power in
$a_{i}a_{j}+\lambda $
is a dth power in
![]() $\mathbb {F}_q^*$
or
$\mathbb {F}_q^*$
or
![]() $0$
for any choice of i and j. Unlike the natural analog for the classical Diophantine tuples (of property
$0$
for any choice of i and j. Unlike the natural analog for the classical Diophantine tuples (of property
![]() $D_{2}(1)$
), it makes sense to talk about the strong Diophantine tuples in
$D_{2}(1)$
), it makes sense to talk about the strong Diophantine tuples in
![]() $\mathbb {F}_q$
. The strong generalized Diophantine tuples with property
$\mathbb {F}_q$
. The strong generalized Diophantine tuples with property
![]() $D_{k}(n)$
in for general k and n are also meaningful to study: the problem of counting the explicit size of the strong generalized Diophantine tuples with property
$D_{k}(n)$
in for general k and n are also meaningful to study: the problem of counting the explicit size of the strong generalized Diophantine tuples with property
![]() $D_k(n)$
involves the problem of counting solutions of the equations appearing in the statement of Pillai’s conjecture. Theorem 1.2 can be improved for strong generalized Diophantine tuples with property
$D_k(n)$
involves the problem of counting solutions of the equations appearing in the statement of Pillai’s conjecture. Theorem 1.2 can be improved for strong generalized Diophantine tuples with property
![]() $D_k(n)$
; see Theorem 5.2.
$D_k(n)$
; see Theorem 5.2.
The generalizations of Diophantine tuples over finite fields are of independent interest. Perhaps the most interesting question to explore is the exact analog of estimating
![]() $M_k(n)$
as discussed in Section 1.1. Indeed, estimating the size of the largest Diophantine tuple with property
$M_k(n)$
as discussed in Section 1.1. Indeed, estimating the size of the largest Diophantine tuple with property
![]() $SD_{d}(\lambda ,\mathbb {F}_{q})$
or with property
$SD_{d}(\lambda ,\mathbb {F}_{q})$
or with property
![]() $D_{d}(\lambda ,\mathbb {F}_{q})$
is of particular interest for the application of Diophantine tuples (over integers) as discussed in [Reference Becker and Murty1, Reference Dixit, Kim and Murty7, Reference Dujella8, Reference Güloğlu and Murty16, Reference Kim, Yip and Yoo24]. Similarly, we denote
$D_{d}(\lambda ,\mathbb {F}_{q})$
is of particular interest for the application of Diophantine tuples (over integers) as discussed in [Reference Becker and Murty1, Reference Dixit, Kim and Murty7, Reference Dujella8, Reference Güloğlu and Murty16, Reference Kim, Yip and Yoo24]. Similarly, we denote
 $$ \begin{align*} MSD_{d}(\lambda,\mathbb{F}_q)&=\sup \{|A| \colon A \subset {\mathbb F}_q^* \text{ satisfies property }SD_{d}(\lambda,\mathbb{F}_q)\}, \quad \text{and}\\ MD_{d}(\lambda,\mathbb{F}_q)&=\sup \{|A| \colon A \subset {\mathbb F}_q^* \text{ satisfies property }D_{d}(\lambda,\mathbb{F}_q)\}. \end{align*} $$
$$ \begin{align*} MSD_{d}(\lambda,\mathbb{F}_q)&=\sup \{|A| \colon A \subset {\mathbb F}_q^* \text{ satisfies property }SD_{d}(\lambda,\mathbb{F}_q)\}, \quad \text{and}\\ MD_{d}(\lambda,\mathbb{F}_q)&=\sup \{|A| \colon A \subset {\mathbb F}_q^* \text{ satisfies property }D_{d}(\lambda,\mathbb{F}_q)\}. \end{align*} $$
Note that when
![]() $\lambda =0$
, it is trivial that
$\lambda =0$
, it is trivial that
![]() $MSD_{d}(\lambda ,\mathbb {F}_q)=MD_{d}(\lambda ,\mathbb {F}_q)=\frac {q-1}{d}$
. Thus, we always assume
$MSD_{d}(\lambda ,\mathbb {F}_q)=MD_{d}(\lambda ,\mathbb {F}_q)=\frac {q-1}{d}$
. Thus, we always assume
![]() $\lambda \neq 0$
throughout the article. In Section 3, we give an upper bound
$\lambda \neq 0$
throughout the article. In Section 3, we give an upper bound
![]() $\sqrt {q}+O(1)$
of
$\sqrt {q}+O(1)$
of
![]() $MSD_{d}(\lambda ,\mathbb {F}_q)$
and
$MSD_{d}(\lambda ,\mathbb {F}_q)$
and
![]() $MD_{d}(\lambda ,\mathbb {F}_q)$
. More precisely, we prove the following proposition using a double character sum estimate. We refer to the bounds in the following proposition as the “trivial” upper bound.
$MD_{d}(\lambda ,\mathbb {F}_q)$
. More precisely, we prove the following proposition using a double character sum estimate. We refer to the bounds in the following proposition as the “trivial” upper bound.
Proposition 1.4 (Trivial upper bound)
Let
![]() $d \geq 2$
and let
$d \geq 2$
and let
![]() $q \equiv 1 \ \pmod d$
be a prime power. Let
$q \equiv 1 \ \pmod d$
be a prime power. Let
![]() $A \subset {\mathbb F}_q^*$
and
$A \subset {\mathbb F}_q^*$
and
![]() $\lambda \in {\mathbb F}_q^*$
. Then
$\lambda \in {\mathbb F}_q^*$
. Then
![]() $MSD_{d}(\lambda ,\mathbb {F}_q) \leq \frac {\sqrt {4q-3}+1}{2}$
and
$MSD_{d}(\lambda ,\mathbb {F}_q) \leq \frac {\sqrt {4q-3}+1}{2}$
and
![]() $MD_{d}(\lambda ,\mathbb {F}_q) \leq \sqrt {q-\frac {11}{4}}+\frac {5}{2}$
.
$MD_{d}(\lambda ,\mathbb {F}_q) \leq \sqrt {q-\frac {11}{4}}+\frac {5}{2}$
.
For the case
![]() $q=p$
, similar bounds of Proposition 1.4 are known previously in [Reference Becker and Murty1, Reference Dixit, Kim and Murty7, Reference Gyarmati17]. On the other hand, Proposition 1.4 gives an almost optimal bound of
$q=p$
, similar bounds of Proposition 1.4 are known previously in [Reference Becker and Murty1, Reference Dixit, Kim and Murty7, Reference Gyarmati17]. On the other hand, Proposition 1.4 gives an almost optimal bound of
![]() $MSD_{d}(\lambda ,\mathbb {F}_q)$
and
$MSD_{d}(\lambda ,\mathbb {F}_q)$
and
![]() $MD_{d}(\lambda ,\mathbb {F}_q)$
when q is a square (Theorem 1.6). Our next theorem improves the trivial upper bounds in Proposition 1.4 by a multiplicative constant factor
$MD_{d}(\lambda ,\mathbb {F}_q)$
when q is a square (Theorem 1.6). Our next theorem improves the trivial upper bounds in Proposition 1.4 by a multiplicative constant factor
![]() $\sqrt {1/d}$
or
$\sqrt {1/d}$
or
![]() $\sqrt {2/d}$
when
$\sqrt {2/d}$
when
![]() $q=p$
is a prime.
$q=p$
is a prime.
Theorem 1.5 Let
![]() $d \geq 2$
. Let
$d \geq 2$
. Let
![]() $p \equiv 1 \ \pmod d$
be a prime and let
$p \equiv 1 \ \pmod d$
be a prime and let
![]() $\lambda \in {\mathbb F}_p^*$
. Then
$\lambda \in {\mathbb F}_p^*$
. Then
-
(1)
 $MSD_{d}(\lambda ,\mathbb {F}_p) \leq \sqrt {(p-1)/d}+1$
. Moreover, if
$MSD_{d}(\lambda ,\mathbb {F}_p) \leq \sqrt {(p-1)/d}+1$
. Moreover, if
 $\lambda $
is a dth power in
$\lambda $
is a dth power in
 ${\mathbb F}_p^*$
, then we have a stronger upper bound:
${\mathbb F}_p^*$
, then we have a stronger upper bound:  $$ \begin{align*}MSD_{d}(\lambda,\mathbb{F}_p)\leq \sqrt{\frac{p-1}{d}-\frac{3}{4}}+\frac{1}{2}.\end{align*} $$
$$ \begin{align*}MSD_{d}(\lambda,\mathbb{F}_p)\leq \sqrt{\frac{p-1}{d}-\frac{3}{4}}+\frac{1}{2}.\end{align*} $$
-
(2)
 $MD_{d}(\lambda ,\mathbb {F}_p) \leq \sqrt {2(p-1)/d}+4$
.
$MD_{d}(\lambda ,\mathbb {F}_p) \leq \sqrt {2(p-1)/d}+4$
.
We remark that our new bound on
![]() $MSD_{d}(\lambda ,\mathbb {F}_p)$
is sometimes sharp. For example, we get a tight bound for a prime
$MSD_{d}(\lambda ,\mathbb {F}_p)$
is sometimes sharp. For example, we get a tight bound for a prime
![]() $p \in \{5,7,11,13,17,23,31,37,41,53,59,61,113\}$
when
$p \in \{5,7,11,13,17,23,31,37,41,53,59,61,113\}$
when
![]() $d=2$
and
$d=2$
and
![]() $\lambda =1$
. See also Theorem 4.7 and Remark 4.8 for a generalization of Theorem 1.5 over general finite fields with non-square order under some extra assumptions.
$\lambda =1$
. See also Theorem 4.7 and Remark 4.8 for a generalization of Theorem 1.5 over general finite fields with non-square order under some extra assumptions.
Nevertheless, in the case of finite fields of square order, we improve Proposition 1.4 by a little bit under some minor assumptions; see Theorem 4.5. Surprisingly, this tiny improvement turns out to be sharp for many infinite families of
![]() $(q,d,\lambda )$
. Equivalently, we determine
$(q,d,\lambda )$
. Equivalently, we determine
![]() $MD_d(\lambda , {\mathbb F}_q)$
and
$MD_d(\lambda , {\mathbb F}_q)$
and
![]() $MSD_d(\lambda , {\mathbb F}_q)$
exactly in those families. In the following theorem, we give a sufficient condition so that
$MSD_d(\lambda , {\mathbb F}_q)$
exactly in those families. In the following theorem, we give a sufficient condition so that
![]() $MD_d(\lambda , {\mathbb F}_q)$
and
$MD_d(\lambda , {\mathbb F}_q)$
and
![]() $MSD_d(\lambda , {\mathbb F}_q)$
can be determined explicitly.
$MSD_d(\lambda , {\mathbb F}_q)$
can be determined explicitly.
Theorem 1.6 Let q be a prime power and a square,
![]() $d \geq 2$
, and
$d \geq 2$
, and
![]() $d \mid (\sqrt {q}+1)$
. Let
$d \mid (\sqrt {q}+1)$
. Let
![]() $S_d=\{x^d: x \in {\mathbb F}_q^*\}$
. Suppose that there is
$S_d=\{x^d: x \in {\mathbb F}_q^*\}$
. Suppose that there is
![]() $\alpha \in {\mathbb F}_q$
such that
$\alpha \in {\mathbb F}_q$
such that
![]() $\alpha ^2 \in S_d$
and
$\alpha ^2 \in S_d$
and
![]() $\lambda \in \alpha ^2 {\mathbb F}_{\sqrt {q}}^*$
(for example, if
$\lambda \in \alpha ^2 {\mathbb F}_{\sqrt {q}}^*$
(for example, if
![]() $\alpha =1$
and
$\alpha =1$
and
![]() $\lambda \in {\mathbb F}_{\sqrt {q}}^*)$
. Suppose further that
$\lambda \in {\mathbb F}_{\sqrt {q}}^*)$
. Suppose further that
![]() $r\leq (p-1)\sqrt {q}$
, where r is the remainder of
$r\leq (p-1)\sqrt {q}$
, where r is the remainder of
![]() $\frac {q-1}{d}$
divided by
$\frac {q-1}{d}$
divided by
![]() $p\sqrt {q}$
. Then
$p\sqrt {q}$
. Then
![]() $MSD_d(\lambda , {\mathbb F}_q)=\sqrt {q}-1$
. If
$MSD_d(\lambda , {\mathbb F}_q)=\sqrt {q}-1$
. If
![]() $q \geq 25$
and
$q \geq 25$
and
![]() $d \geq 3$
, then we have the stronger conclusion that
$d \geq 3$
, then we have the stronger conclusion that
![]() $MD_d(\lambda , {\mathbb F}_q)=\sqrt {q}-1$
.
$MD_d(\lambda , {\mathbb F}_q)=\sqrt {q}-1$
.
Under the assumptions on Theorem 1.6,
![]() $\alpha {\mathbb F}_{\sqrt {q}}^*$
satisfies the required property
$\alpha {\mathbb F}_{\sqrt {q}}^*$
satisfies the required property
![]() $SD_{d}(\lambda ,\mathbb {F}_q)$
and
$SD_{d}(\lambda ,\mathbb {F}_q)$
and
![]() $D_{d}(\lambda ,\mathbb {F}_q)$
. Compared to Theorem 1.5, it is tempting to conjecture that such an algebraic construction (which is unique to finite fields with proper prime power order) is the optimal one with the required property. Given Proposition 1.4, to show such construction is optimal, it suffices to rule out the possibility of a Diophantine tuple with property
$D_{d}(\lambda ,\mathbb {F}_q)$
. Compared to Theorem 1.5, it is tempting to conjecture that such an algebraic construction (which is unique to finite fields with proper prime power order) is the optimal one with the required property. Given Proposition 1.4, to show such construction is optimal, it suffices to rule out the possibility of a Diophantine tuple with property
![]() $SD_{d}(\lambda ,\mathbb {F}_q)$
and
$SD_{d}(\lambda ,\mathbb {F}_q)$
and
![]() $D_{d}(\lambda ,\mathbb {F}_q)$
of size
$D_{d}(\lambda ,\mathbb {F}_q)$
of size
![]() $\sqrt {q}$
. While this seems easy, it turned out that this requires non-trivial efforts.
$\sqrt {q}$
. While this seems easy, it turned out that this requires non-trivial efforts.
Next, we give concrete examples where Theorem 1.6 applies.
Example 1.7 Note that a Diophantine tuple with property
![]() $SD_2(1, {\mathbb F}_q)$
corresponds to a strong Diophantine tuple over
$SD_2(1, {\mathbb F}_q)$
corresponds to a strong Diophantine tuple over
![]() ${\mathbb F}_q$
. If q is an odd square, Theorem 1.6 implies that the largest size of a strong Diophantine tuple over
${\mathbb F}_q$
. If q is an odd square, Theorem 1.6 implies that the largest size of a strong Diophantine tuple over
![]() ${\mathbb F}_q$
is given by
${\mathbb F}_q$
is given by
![]() $\sqrt {q}-1$
, which is achieved by
$\sqrt {q}-1$
, which is achieved by
![]() ${\mathbb F}_{\sqrt {q}}^*$
. Note that in this case we have
${\mathbb F}_{\sqrt {q}}^*$
. Note that in this case we have
![]() $r=\frac {p\sqrt {q}-1}{2}<(p-1)\sqrt {q}$
.
$r=\frac {p\sqrt {q}-1}{2}<(p-1)\sqrt {q}$
.
We also consider the case that
![]() $d=3$
,
$d=3$
,
![]() $d \mid (\sqrt {q}+1)$
, and
$d \mid (\sqrt {q}+1)$
, and
![]() $\lambda =1$
. In this case, Theorem 1.6 also applies. Note that
$\lambda =1$
. In this case, Theorem 1.6 also applies. Note that
![]() $3 \mid (\sqrt {q}+1)$
implies that
$3 \mid (\sqrt {q}+1)$
implies that
![]() $p \equiv 2 \ \pmod 3$
, in which case the base-p representation of
$p \equiv 2 \ \pmod 3$
, in which case the base-p representation of
![]() $\frac {q-1}{3}$
only contains the digit
$\frac {q-1}{3}$
only contains the digit
![]() $\frac {p-2}{3}$
and
$\frac {p-2}{3}$
and
![]() $\frac {2p-1}{3}$
, so that the condition
$\frac {2p-1}{3}$
, so that the condition
![]() $r \leq (p-1)\sqrt {q}$
holds.
$r \leq (p-1)\sqrt {q}$
holds.
One key ingredient of the proofs of Theorems 1.5 and 1.6 is Theorem 1.1. Indeed, Theorem 1.1 can also be viewed as on an upper bound of a bipartite version of Diophantine tuples over finite fields. For the applications to strong Diophantine tuples, Theorem 1.1 is sufficient. On the other hand, to obtain upper bounds on Diophantine tuples (which are not necessarily strong Diophantine tuples), we also need a version of Theorem 1.1 for restricted product sets, which can be found as Theorem 4.2. Indeed, Theorem 1.1 alone only implies a weaker bound of the form
![]() $2\sqrt {p/d}$
for
$2\sqrt {p/d}$
for
![]() $MSD_d(\lambda , {\mathbb F}_p)$
; see Remark 4.3.
$MSD_d(\lambda , {\mathbb F}_p)$
; see Remark 4.3.
1.3 Multiplicative decompositions of shifted multiplicative subgroups
A well-known conjecture of Sárközy [Reference Sárközy30] asserts that the set of nonzero squares
![]() $S_2=\{x^2: x \in {\mathbb F}_p^*\} \subset {\mathbb F}_p$
cannot be written as
$S_2=\{x^2: x \in {\mathbb F}_p^*\} \subset {\mathbb F}_p$
cannot be written as
![]() $S_2=A+B$
, where
$S_2=A+B$
, where
![]() $A,B \subset {\mathbb F}_p$
and
$A,B \subset {\mathbb F}_p$
and
![]() $|A|, |B| \geq 2$
, provided that p is a sufficiently large prime. This conjecture essentially predicts that the set of quadratic residues in a prime field cannot have a rich additive structure. Similarly, one expects that any non-trivial shift of
$|A|, |B| \geq 2$
, provided that p is a sufficiently large prime. This conjecture essentially predicts that the set of quadratic residues in a prime field cannot have a rich additive structure. Similarly, one expects that any non-trivial shift of
![]() $S_2$
cannot have a rich multiplicative structure. Indeed, this can be made precise via another interesting conjecture of Sárközy [Reference Sárközy31], which we make progress in the current article.
$S_2$
cannot have a rich multiplicative structure. Indeed, this can be made precise via another interesting conjecture of Sárközy [Reference Sárközy31], which we make progress in the current article.
Conjecture 1.8 (Sárközy)
If p is a sufficiently large prime and
![]() $\lambda \in {\mathbb F}_p^*$
, then the shifted subgroup
$\lambda \in {\mathbb F}_p^*$
, then the shifted subgroup
![]() $(S_2-\lambda )\setminus \{0\}$
cannot be written as the product
$(S_2-\lambda )\setminus \{0\}$
cannot be written as the product
![]() $AB$
, where
$AB$
, where
![]() $A,B \subset {\mathbb F}_p^*$
and
$A,B \subset {\mathbb F}_p^*$
and
![]() $|A|, |B| \geq 2$
. In other words,
$|A|, |B| \geq 2$
. In other words,
![]() $(S_2-\lambda )\setminus \{0\}$
has no non-trivial multiplicative decomposition.
$(S_2-\lambda )\setminus \{0\}$
has no non-trivial multiplicative decomposition.
We note that it is necessary to take out the element
![]() $0$
from the shifted subgroup, for otherwise one can always decompose
$0$
from the shifted subgroup, for otherwise one can always decompose
![]() $S_2-\lambda $
as
$S_2-\lambda $
as
![]() $\{0,1\} \cdot (S_2-\lambda )$
. It appears that this problem concerning multiplicative decompositions is more difficult than the one concerning additive decompositions stated previously, given that it might depend on the parameter
$\{0,1\} \cdot (S_2-\lambda )$
. It appears that this problem concerning multiplicative decompositions is more difficult than the one concerning additive decompositions stated previously, given that it might depend on the parameter
![]() $\lambda $
. Inspired by Conjecture 1.8, we formulate the following more general conjecture for any proper multiplicative subgroup. For simplicity, we denote
$\lambda $
. Inspired by Conjecture 1.8, we formulate the following more general conjecture for any proper multiplicative subgroup. For simplicity, we denote
![]() $S_d=S_d({\mathbb F}_q)=\{x^d: x \in {\mathbb F}_q^*\}$
to be the set of dth powers in
$S_d=S_d({\mathbb F}_q)=\{x^d: x \in {\mathbb F}_q^*\}$
to be the set of dth powers in
![]() ${\mathbb F}_q^*$
, equivalently, the subgroup of
${\mathbb F}_q^*$
, equivalently, the subgroup of
![]() ${\mathbb F}_q^*$
with order
${\mathbb F}_q^*$
with order
![]() $\frac {q-1}{d}$
.
$\frac {q-1}{d}$
.
Conjecture 1.9 Let
![]() $d \geq 2$
. If
$d \geq 2$
. If
![]() $q \equiv 1 \ \pmod d$
is a sufficiently large prime power, then for any
$q \equiv 1 \ \pmod d$
is a sufficiently large prime power, then for any
![]() $\lambda \in {\mathbb F}_q^*$
,
$\lambda \in {\mathbb F}_q^*$
,
![]() $(S_d-\lambda )\setminus \{0\}$
does not admit a non-trivial multiplicative decomposition, that is, there do not exist two sets
$(S_d-\lambda )\setminus \{0\}$
does not admit a non-trivial multiplicative decomposition, that is, there do not exist two sets
![]() $A,B \subset {\mathbb F}_q^*$
with
$A,B \subset {\mathbb F}_q^*$
with
![]() $|A|,|B| \geq 2$
, such that
$|A|,|B| \geq 2$
, such that
![]() $(S_d-\lambda )\setminus \{0\}=AB$
.
$(S_d-\lambda )\setminus \{0\}=AB$
.
Conjecture 1.9 predicts that a shifted multiplicative subgroup of a finite field admits a non-trivial multiplicative decomposition only when it has a small size. We remark that the integer version of Conjecture 1.9, namely, for each
![]() $k \geq 2$
, a non-trivial shift of kth powers in integers has no non-trivial multiplicative decomposition, has been proved and strengthened in a series of papers by Hajdu and Sárközy [Reference Hajdu and Sárközy18–Reference Hajdu and Sárközy20]. On the other hand, to the best knowledge of the authors, Conjecture 1.9 appears to be much harder and no partial progress has been made. For the analog of Conjecture 1.9 on the additive decomposition of multiplicative subgroups, we refer to recent papers [Reference Hanson and Petridis21, Reference Sárközy31, Reference Shkredov33, Reference Yip38] for an extensive discussion on partial progress.
$k \geq 2$
, a non-trivial shift of kth powers in integers has no non-trivial multiplicative decomposition, has been proved and strengthened in a series of papers by Hajdu and Sárközy [Reference Hajdu and Sárközy18–Reference Hajdu and Sárközy20]. On the other hand, to the best knowledge of the authors, Conjecture 1.9 appears to be much harder and no partial progress has been made. For the analog of Conjecture 1.9 on the additive decomposition of multiplicative subgroups, we refer to recent papers [Reference Hanson and Petridis21, Reference Sárközy31, Reference Shkredov33, Reference Yip38] for an extensive discussion on partial progress.
Our main contribution to Conjecture 1.9 is the following two results. The first one is a corollary of Theorem 1.1.
Corollary 1.10 Let
![]() $d \geq 2$
and p be a prime such that
$d \geq 2$
and p be a prime such that
![]() $d \mid (p-1)$
. Let
$d \mid (p-1)$
. Let
![]() $\lambda \in S_d$
. If
$\lambda \in S_d$
. If
![]() $(S_d-\lambda ) \setminus \{0\}$
can be multiplicative decomposed as the product of two sets
$(S_d-\lambda ) \setminus \{0\}$
can be multiplicative decomposed as the product of two sets
![]() $A,B \subset {\mathbb F}_p^*$
with
$A,B \subset {\mathbb F}_p^*$
with
![]() $|A|,|B| \geq 2$
, then we must have
$|A|,|B| \geq 2$
, then we must have
![]() $|A||B|=|S_d|-1$
, that is, all products
$|A||B|=|S_d|-1$
, that is, all products
![]() $ab$
are distinct. In other words,
$ab$
are distinct. In other words,
![]() $A,B$
are multiplicatively co-Sidon.
$A,B$
are multiplicatively co-Sidon.
In particular, Corollary 1.10 confirms Conjecture 1.9 under the assumption that q is a prime,
![]() $\lambda \in S_d$
, and
$\lambda \in S_d$
, and
![]() $|S_d|-1$
is a prime. The second result provides a partial answer to Conjecture 1.9 asymptotically.
$|S_d|-1$
is a prime. The second result provides a partial answer to Conjecture 1.9 asymptotically.
Theorem 1.11 Let
![]() $d \geq 2$
be fixed and n be a positive integer. As
$d \geq 2$
be fixed and n be a positive integer. As
![]() $x \to \infty $
, the number of primes
$x \to \infty $
, the number of primes
![]() $p \leq x$
such that
$p \leq x$
such that
![]() $p \equiv 1 \ \pmod d$
and
$p \equiv 1 \ \pmod d$
and
![]() $(S_d({\mathbb F}_p)-n) \setminus \{0\}$
has no non-trivial multiplicative decomposition is at least
$(S_d({\mathbb F}_p)-n) \setminus \{0\}$
has no non-trivial multiplicative decomposition is at least
 $$ \begin{align*}\bigg(\frac{1}{[\mathbb{Q}(e^{2\pi i/d}, n^{1/d}):\mathbb{Q}]}-o(1)\bigg)\pi(x).\end{align*} $$
$$ \begin{align*}\bigg(\frac{1}{[\mathbb{Q}(e^{2\pi i/d}, n^{1/d}):\mathbb{Q}]}-o(1)\bigg)\pi(x).\end{align*} $$
In particular, by setting
![]() $n=1$
and
$n=1$
and
![]() $d=2$
, our result has the following significant implication to Sárközy’s conjecture [Reference Sárközy31]: for almost all odd primes p, the shifted multiplicative subgroup
$d=2$
, our result has the following significant implication to Sárközy’s conjecture [Reference Sárközy31]: for almost all odd primes p, the shifted multiplicative subgroup
![]() $(S_2({\mathbb F}_p)-1)\setminus \{0\}$
has no non-trivial multiplicative decomposition. In other words, if
$(S_2({\mathbb F}_p)-1)\setminus \{0\}$
has no non-trivial multiplicative decomposition. In other words, if
![]() $\lambda =1$
, then Sárközy’s conjecture holds for almost all primes p; see Theorem 6.1 for a precise statement.
$\lambda =1$
, then Sárközy’s conjecture holds for almost all primes p; see Theorem 6.1 for a precise statement.
Some partial progress has been made for Conjecture 1.9 when the multiplicative decomposition is assumed to have special forms [Reference Sárközy31, Reference Shkredov33]. We also make progress in this direction in Section 6.2. In particular, in Theorem 6.6, we confirm the ternary version of Conjecture 1.9 in a strong sense, which generalizes [Reference Sárközy31, Theorem 2].
Notations. We follow standard notations from analytic number theory. We use
![]() $\pi $
and
$\pi $
and
![]() $\theta $
to denote the standard prime-counting functions. We adopt standard asymptotic notations
$\theta $
to denote the standard prime-counting functions. We adopt standard asymptotic notations
![]() $O, o, \asymp $
. We also follow the Vinogradov notation
$O, o, \asymp $
. We also follow the Vinogradov notation
![]() $\ll $
: we write
$\ll $
: we write
![]() $X \ll Y$
if there is an absolute constant
$X \ll Y$
if there is an absolute constant
![]() $C>0$
so that
$C>0$
so that
![]() $|X| \leq CY$
.
$|X| \leq CY$
.
Throughout the article, let p be a prime and q a power of p. Let
![]() ${\mathbb F}_q$
be the finite field with q elements and let
${\mathbb F}_q$
be the finite field with q elements and let
![]() ${\mathbb F}_q^*={\mathbb F}_q \setminus \{0\}$
. We always assume that
${\mathbb F}_q^*={\mathbb F}_q \setminus \{0\}$
. We always assume that
![]() $d \mid (q-1)$
with
$d \mid (q-1)$
with
![]() $d \ge 2$
, and denote
$d \ge 2$
, and denote
![]() $S_d({\mathbb F}_q)=\{x^d: x \in {\mathbb F}_q^*\}$
to be the subgroup of
$S_d({\mathbb F}_q)=\{x^d: x \in {\mathbb F}_q^*\}$
to be the subgroup of
![]() ${\mathbb F}_q^*$
with order
${\mathbb F}_q^*$
with order
![]() $\frac {q-1}{d}$
. If q is assumed to be fixed, for brevity, we simply write
$\frac {q-1}{d}$
. If q is assumed to be fixed, for brevity, we simply write
![]() $S_d$
instead of
$S_d$
instead of
![]() $S_d({\mathbb F}_q)$
.
$S_d({\mathbb F}_q)$
.
We also need some notations for arithmetic operations among sets. Given two sets A and B, we write the product set
![]() $AB=\{ab: a \in A, b \in B\}$
, and the sumset
$AB=\{ab: a \in A, b \in B\}$
, and the sumset
![]() $A+B=\{a+b: a \in A, b \in B\}$
. Given the definition of Diophantine tuples, it is also useful to define the restricted product set of A, that is,
$A+B=\{a+b: a \in A, b \in B\}$
. Given the definition of Diophantine tuples, it is also useful to define the restricted product set of A, that is,
![]() $A \hat {\times } A=\{ab: a,b \in A, a \neq b\}$
.
$A \hat {\times } A=\{ab: a,b \in A, a \neq b\}$
.
Structure of the article. In Section 2, we introduce more background. In Section 3, using Gauss sums and Weil’s bound, we give an upper bound on the size of the set which satisfies various multiplicative properties based on character sum estimates. In particular, we prove Proposition 1.4. In Section 4, we first prove Theorem 1.1 using Stepanov’s method. At the end of the section, we deduce applications of Theorem 1.1 to Diophantine tuples and prove Theorems 1.5 and 1.6. Via Gallagher’s larger sieve inequality and other tools from analytic number theory, in Section 5, we prove Theorems 1.2 and 1.3. In Section 6, we study multiplicative decompositions and prove Theorem 1.11.
2 Background
2.1 Stepanov’s method
We first describe Stepanov’s method [Reference Stepanov35]. If we can construct a low degree non-zero auxiliary polynomial that vanishes on each element of a set A with high multiplicity, then we can give an upper bound on
![]() $|A|$
based on the degree of the polynomial. It turns out that the most challenging part of our proofs is to show that the auxiliary polynomial constructed is not identically zero.
$|A|$
based on the degree of the polynomial. It turns out that the most challenging part of our proofs is to show that the auxiliary polynomial constructed is not identically zero.
To check that each root has a high multiplicity, standard derivatives might not work since we are working in a field with characteristic p. To resolve this issue, we need the following notation of derivatives, known as the Hasse derivatives or hyper-derivatives; see [Reference Lidl and Niederreiter26, Section 6.4].
Definition 2.1 Let
![]() $c_0,c_1, \ldots c_d \in {\mathbb F}_q$
. If n is a non-negative integer, then the nth hyper-derivative of
$c_0,c_1, \ldots c_d \in {\mathbb F}_q$
. If n is a non-negative integer, then the nth hyper-derivative of
![]() $f(x)=\sum _{j=0}^d c_j x^j$
is
$f(x)=\sum _{j=0}^d c_j x^j$
is
 $$ \begin{align*}E^{(n)}(f) =\sum_{j=0}^d \binom{j}{n} c_j x^{j-n}, \end{align*} $$
$$ \begin{align*}E^{(n)}(f) =\sum_{j=0}^d \binom{j}{n} c_j x^{j-n}, \end{align*} $$
where we follow the standard convention that
![]() $\binom {j}{n}=0$
for
$\binom {j}{n}=0$
for
![]() $j<n$
, so that the nth hyper-derivative is a polynomial.
$j<n$
, so that the nth hyper-derivative is a polynomial.
Following the definition, we have
![]() $E^{(0)}f=f$
. We also need the next three lemmas.
$E^{(0)}f=f$
. We also need the next three lemmas.
Lemma 2.2 [Reference Lidl and Niederreiter26, Lemma 6.47]
If
![]() $f, g \in {\mathbb F}_q[x]$
, then
$f, g \in {\mathbb F}_q[x]$
, then
 $$ \begin{align*}E^{(n)}(fg)= \sum_{k=0}^n E^{(k)} (f) E^{(n-k)} (g).\end{align*} $$
$$ \begin{align*}E^{(n)}(fg)= \sum_{k=0}^n E^{(k)} (f) E^{(n-k)} (g).\end{align*} $$
Lemma 2.3 [Reference Lidl and Niederreiter26, Corollary 6.48]
Let
![]() $n,d$
be positive integers. If
$n,d$
be positive integers. If
![]() $a\in {\mathbb F}^{*}_q$
and
$a\in {\mathbb F}^{*}_q$
and
![]() $c \in {\mathbb F}_q$
, then we have
$c \in {\mathbb F}_q$
, then we have
Lemma 2.4 [Reference Lidl and Niederreiter26, Lemma 6.51]
Let f be a non-zero polynomial in
![]() ${\mathbb F}_q[x]$
. If c is a root of
${\mathbb F}_q[x]$
. If c is a root of
![]() $E^{(k)}(f)$
for
$E^{(k)}(f)$
for
![]() $k=0,1,\ldots , m-1$
, then c is a root of multiplicity at least m.
$k=0,1,\ldots , m-1$
, then c is a root of multiplicity at least m.
2.2 Gallagher’s larger sieve inequality
In this subsection, we introduce Gallagher’s larger sieve inequality and provide necessary estimations from it. Gallagher’s larger sieve inequality will be one of the main ingredients for the proof of Theorem 1.2. In 1971, Gallagher [Reference Gallagher15] discovered the following sieve inequality.
Theorem 2.5 (Gallagher’s larger sieve inequality)
Let N be a natural number and
![]() $A\subset \{1,2,\ldots , N\}$
. Let
$A\subset \{1,2,\ldots , N\}$
. Let
![]() ${\mathcal P}$
be a set of primes. For each prime
${\mathcal P}$
be a set of primes. For each prime
![]() $p \in {\mathcal P}$
, let
$p \in {\mathcal P}$
, let
![]() $A_p=A \ \pmod {p}$
. For any
$A_p=A \ \pmod {p}$
. For any
![]() $1<Q\leq N$
, we have
$1<Q\leq N$
, we have
 $$ \begin{align} |A|\leq \frac{\underset{p\leq Q, p\in \mathcal{P}}\sum\log p - \log N}{\underset{p\leq Q, p \in \mathcal{P}}\sum\frac{\log p}{|A_p|}-\log N}, \end{align} $$
$$ \begin{align} |A|\leq \frac{\underset{p\leq Q, p\in \mathcal{P}}\sum\log p - \log N}{\underset{p\leq Q, p \in \mathcal{P}}\sum\frac{\log p}{|A_p|}-\log N}, \end{align} $$
provided that the denominator is positive.
As a preparation to apply Gallagher’s larger sieve in our proof, we need to establish a few estimates related to primes in arithmetic progressions. For
![]() $(a,k)=1$
, we follow the standard notation
$(a,k)=1$
, we follow the standard notation
 $$\begin{align*}\theta(x;k,a)=\sum_{\substack{p\leq x \\ p\equiv a \text{ mod } k}} \log p.\end{align*}$$
$$\begin{align*}\theta(x;k,a)=\sum_{\substack{p\leq x \\ p\equiv a \text{ mod } k}} \log p.\end{align*}$$
For our purposes,
![]() $\log k$
could be as large as
$\log k$
could be as large as
![]() $\sqrt {\log \log x}$
(for example, see Theorem 1.2), and we need the Siegel–Walfisz theorem to estimate
$\sqrt {\log \log x}$
(for example, see Theorem 1.2), and we need the Siegel–Walfisz theorem to estimate
![]() $\theta (x;k,a)$
.
$\theta (x;k,a)$
.
Lemma 2.6 [Reference Montgomery and Vaughan28, Corollary 11.21]
Let
![]() $A>0$
be a constant. There is a constant
$A>0$
be a constant. There is a constant
![]() $c_1>0$
such that
$c_1>0$
such that
 $$\begin{align*}\theta(Q;k,a)=\frac{Q}{\phi(k)} +O_A\bigg(Q\exp(-c_1\sqrt{\log Q})\bigg)\end{align*}$$
$$\begin{align*}\theta(Q;k,a)=\frac{Q}{\phi(k)} +O_A\bigg(Q\exp(-c_1\sqrt{\log Q})\bigg)\end{align*}$$
holds uniformly for
![]() $k\leq (\log Q)^A$
and
$k\leq (\log Q)^A$
and
![]() $(a,k)=1$
.
$(a,k)=1$
.
A standard application of partial summation with Lemma 2.6 leads to the following corollary.
Corollary 2.7 There is a constant
![]() $c>0$
, such that
$c>0$
, such that
 $$ \begin{align*}\sum_{\substack{p \leq Q\\ p \equiv a \text{ mod } k}} \frac{\log p}{\sqrt{p}}=\frac{2\sqrt{Q}}{\phi(k)} +O\left( \sqrt{Q} \exp(-c\sqrt{\log Q}) \right) \end{align*} $$
$$ \begin{align*}\sum_{\substack{p \leq Q\\ p \equiv a \text{ mod } k}} \frac{\log p}{\sqrt{p}}=\frac{2\sqrt{Q}}{\phi(k)} +O\left( \sqrt{Q} \exp(-c\sqrt{\log Q}) \right) \end{align*} $$
holds uniformly for
![]() $k \leq \log Q$
and
$k \leq \log Q$
and
![]() $(a,k)=1$
.
$(a,k)=1$
.
We also need the following lemma.
Lemma 2.8 [Reference Becker and Murty1, p. 72]
Let n be a positive integer. Then
 $$ \begin{align*}\sum_{p \mid n} \frac{\log p}{\sqrt{p}} \ll (\log n)^{1/2}. \end{align*} $$
$$ \begin{align*}\sum_{p \mid n} \frac{\log p}{\sqrt{p}} \ll (\log n)^{1/2}. \end{align*} $$
2.3 An effective estimate for
 $M_k(n, \frac {k}{k-2})$
$M_k(n, \frac {k}{k-2})$
Following [Reference Dixit, Kim and Murty7], for each real number
![]() $L>0$
, we write
$L>0$
, we write
It is shown in [Reference Dixit, Kim and Murty7] that
![]() $M_k(n,3) \ll _{k} 1$
as
$M_k(n,3) \ll _{k} 1$
as
![]() $n \to \infty $
. For our application, we show a stronger result that
$n \to \infty $
. For our application, we show a stronger result that
![]() $M_k(n,\frac {k}{k-2})\ll _{k} 1$
and we will make this estimate explicit and effective. We follow the proof in [Reference Dixit, Kim and Murty7] closely and prove the following proposition, which will be used later in the proof of Theorem 1.2.
$M_k(n,\frac {k}{k-2})\ll _{k} 1$
and we will make this estimate explicit and effective. We follow the proof in [Reference Dixit, Kim and Murty7] closely and prove the following proposition, which will be used later in the proof of Theorem 1.2.
Proposition 2.9 If
![]() $k \geq 3$
and
$k \geq 3$
and
![]() $n>(2ke)^{k^2}$
, then
$n>(2ke)^{k^2}$
, then
![]() $M_k(n,\frac {k}{k-2})\ll \log k \log \log k$
, where the implicit constant is absolute.
$M_k(n,\frac {k}{k-2})\ll \log k \log \log k$
, where the implicit constant is absolute.
Let
![]() $k \geq 3$
. Let
$k \geq 3$
. Let
![]() $m= M_k(n,\frac {k}{k-2})$
and
$m= M_k(n,\frac {k}{k-2})$
and
![]() $A=\{a_1, a_2, \ldots , a_m\}$
be a generalized m-tuple with property
$A=\{a_1, a_2, \ldots , a_m\}$
be a generalized m-tuple with property
![]() $D_k(n)$
and
$D_k(n)$
and
![]() $n^{\frac {k}{k-2}} < a_1<a_2<\cdots <a_m$
. Consider the system of equations
$n^{\frac {k}{k-2}} < a_1<a_2<\cdots <a_m$
. Consider the system of equations
 $$ \begin{align} \left\{ \begin{array}{@{}ll} a_1 x + n = u^k &\\ a_2 x + n = v^k. & \end{array} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{array}{@{}ll} a_1 x + n = u^k &\\ a_2 x + n = v^k. & \end{array} \right. \end{align} $$
Clearly, for each
![]() $i \geq 3$
,
$i \geq 3$
,
![]() $x=a_i$
is a solution to this system, and we denote
$x=a_i$
is a solution to this system, and we denote
![]() $u_i, v_i$
so that
$u_i, v_i$
so that
![]() $a_1a_i+n=u_i^k$
and
$a_1a_i+n=u_i^k$
and
![]() $a_2a_i+n=v_i^k$
. Let
$a_2a_i+n=v_i^k$
. Let
![]() $\alpha :=(a_1/a_2)^{1/k}$
.
$\alpha :=(a_1/a_2)^{1/k}$
.
The following lemma is a generalization of [Reference Dixit, Kim and Murty7, Lemma 3.1], showing that
![]() $u_i/v_i$
provides a “good” rational approximation to
$u_i/v_i$
provides a “good” rational approximation to
![]() $\alpha $
if n is large. Note that in [Reference Dixit, Kim and Murty7, Lemma 3.1], it was further assumed that k is odd and
$\alpha $
if n is large. Note that in [Reference Dixit, Kim and Murty7, Lemma 3.1], it was further assumed that k is odd and
![]() $L=3$
. Nevertheless, an almost identical proof works, and we skip the proof.
$L=3$
. Nevertheless, an almost identical proof works, and we skip the proof.
Lemma 2.10 Let
 $$ \begin{align*} c(k):= \prod_{j=1}^{\lfloor (k-1)/2\rfloor} \left(\sin \frac{2\pi j}{k}\right)^2. \end{align*} $$
$$ \begin{align*} c(k):= \prod_{j=1}^{\lfloor (k-1)/2\rfloor} \left(\sin \frac{2\pi j}{k}\right)^2. \end{align*} $$
Assume that
![]() $n> (2/c(k))^{(k-2)/2}$
. Then for each
$n> (2/c(k))^{(k-2)/2}$
. Then for each
![]() $3 \leq i \leq m$
, we have
$3 \leq i \leq m$
, we have
 $$ \begin{align} \bigg|\frac{u_i}{v_i} - \alpha\bigg| \leq \frac{a_2}{2v_i^k}. \end{align} $$
$$ \begin{align} \bigg|\frac{u_i}{v_i} - \alpha\bigg| \leq \frac{a_2}{2v_i^k}. \end{align} $$
Corollary 2.11 Assume that
![]() $n> (2/c(k))^{(k-2)/2}$
. Then
$n> (2/c(k))^{(k-2)/2}$
. Then
![]() $v_i \geq a_2^{4}$
for each
$v_i \geq a_2^{4}$
for each
![]() $14 \leq i \leq m$
and
$14 \leq i \leq m$
and
 $$ \begin{align} \bigg|\frac{u_i}{v_i} - \alpha \bigg| < \frac{1}{v_i^{k-1/2}}. \end{align} $$
$$ \begin{align} \bigg|\frac{u_i}{v_i} - \alpha \bigg| < \frac{1}{v_i^{k-1/2}}. \end{align} $$
Proof Let
![]() $2 \leq i \leq m-3$
. Applying the gap principle from [Reference Dixit, Kim and Murty7, Lemma 2.4] to
$2 \leq i \leq m-3$
. Applying the gap principle from [Reference Dixit, Kim and Murty7, Lemma 2.4] to
![]() $a_i, a_{i+1},a_{i+2}, a_{i+3}$
, we have
$a_i, a_{i+1},a_{i+2}, a_{i+3}$
, we have
It follows that
In particular
![]() $a_{14} \geq a_2^{(k-1)^4}\geq a_2^{4k}$
. Thus, if
$a_{14} \geq a_2^{(k-1)^4}\geq a_2^{4k}$
. Thus, if
![]() $i \geq 14$
, then
$i \geq 14$
, then
![]() $v_i \geq a_i^{1/k} \geq a_{14}^{1/k} \geq a_2^4$
and inequality (2.5) follows from Lemma 2.10.
$v_i \geq a_i^{1/k} \geq a_{14}^{1/k} \geq a_2^4$
and inequality (2.5) follows from Lemma 2.10.
Now we are ready to prove Proposition 2.9. Recall we have the inequality
![]() $\sin x \geq \frac {2x}{\pi }$
for
$\sin x \geq \frac {2x}{\pi }$
for
![]() $x \in [0,\frac {\pi }{2}]$
, and the inequality
$x \in [0,\frac {\pi }{2}]$
, and the inequality
![]() $s! \geq (s/e)^s $
for all positive integers s. It follows that
$s! \geq (s/e)^s $
for all positive integers s. It follows that
 $$ \begin{align*}\sqrt{c(k)}=\prod_{j=1}^{(k-1)/2} \sin \frac{2\pi j}{k}=\prod_{j=1}^{(k-1)/2} \sin \frac{\pi j}{k} \geq \prod_{j=1}^{(k-1)/2} \frac{2j}{k}=\frac{((k-1)/2)!}{(k/2)^{(k-1)/2}} \geq \bigg(\frac{k-1}{ke}\bigg)^{(k-1)/2} \end{align*} $$
$$ \begin{align*}\sqrt{c(k)}=\prod_{j=1}^{(k-1)/2} \sin \frac{2\pi j}{k}=\prod_{j=1}^{(k-1)/2} \sin \frac{\pi j}{k} \geq \prod_{j=1}^{(k-1)/2} \frac{2j}{k}=\frac{((k-1)/2)!}{(k/2)^{(k-1)/2}} \geq \bigg(\frac{k-1}{ke}\bigg)^{(k-1)/2} \end{align*} $$
when k is odd, and
 $$ \begin{align*}(c(k))^{1/4} &=\sqrt{\prod_{j=1}^{(k-2)/2} \sin \frac{2\pi j}{k}}=\prod_{j=1}^{\lfloor k/4 \rfloor} \sin \frac{\pi j}{k/2} \geq \prod_{j=1}^{\lfloor k/4 \rfloor} \frac{4j}{k} \\ &=\frac{(\lfloor k/4 \rfloor)!}{(k/4)^{\lfloor k/4 \rfloor}} \geq \bigg(\frac{4\lfloor k/4 \rfloor}{ke}\bigg)^{\lfloor k/4 \rfloor} \end{align*} $$
$$ \begin{align*}(c(k))^{1/4} &=\sqrt{\prod_{j=1}^{(k-2)/2} \sin \frac{2\pi j}{k}}=\prod_{j=1}^{\lfloor k/4 \rfloor} \sin \frac{\pi j}{k/2} \geq \prod_{j=1}^{\lfloor k/4 \rfloor} \frac{4j}{k} \\ &=\frac{(\lfloor k/4 \rfloor)!}{(k/4)^{\lfloor k/4 \rfloor}} \geq \bigg(\frac{4\lfloor k/4 \rfloor}{ke}\bigg)^{\lfloor k/4 \rfloor} \end{align*} $$
when k is even. Thus, when
![]() $k \geq 3$
, we always have
$k \geq 3$
, we always have
 $$ \begin{align*}\frac{2}{c(k)}\leq 2\bigg(\frac{ke}{k-2}\bigg)^{k} \leq 2(ke)^k. \end{align*} $$
$$ \begin{align*}\frac{2}{c(k)}\leq 2\bigg(\frac{ke}{k-2}\bigg)^{k} \leq 2(ke)^k. \end{align*} $$
Therefore, when
![]() $n>(2ke)^{k^2}$
, we can apply Lemma 2.10. Note that the absolute height of
$n>(2ke)^{k^2}$
, we can apply Lemma 2.10. Note that the absolute height of
![]() $\alpha $
is
$\alpha $
is
![]() $H(\alpha ) \leq a_2^{1/k}$
. Since
$H(\alpha ) \leq a_2^{1/k}$
. Since
![]() $k \geq 3$
, for
$k \geq 3$
, for
![]() $14\leq i \leq m$
, Lemma 2.10 implies that
$14\leq i \leq m$
, Lemma 2.10 implies that
 $$ \begin{align*} \left| \frac{u_i}{v_i} - \alpha\right| \leq \frac{1}{v_i^{k-1/2}} \leq \frac{1}{v_i^{2.5}}; \end{align*} $$
$$ \begin{align*} \left| \frac{u_i}{v_i} - \alpha\right| \leq \frac{1}{v_i^{k-1/2}} \leq \frac{1}{v_i^{2.5}}; \end{align*} $$
moreover,
![]() $\max (u_i,v_i) = v_i>a_2^{1/k} \geq \max (H(\alpha ), 2)$
. Therefore, we can apply the quantitative Roth’s theorem due to Evertse [Reference Evertse12] (see also [Reference Dixit, Kim and Murty7, Theorem 2.2]) to conclude that
$\max (u_i,v_i) = v_i>a_2^{1/k} \geq \max (H(\alpha ), 2)$
. Therefore, we can apply the quantitative Roth’s theorem due to Evertse [Reference Evertse12] (see also [Reference Dixit, Kim and Murty7, Theorem 2.2]) to conclude that
where the implicit constant is absolute.
2.4 Implications of the Paley graph conjecture
The Paley graph conjecture on double character sums implies many results of the present article related to the estimation of character sums. We record the statement of the conjecture (see for example [Reference Dixit, Kim and Murty7, Reference Güloğlu and Murty16]).
Conjecture 2.12 (Paley graph conjecture)
Let
![]() $\epsilon>0$
be a real number. Then there is
$\epsilon>0$
be a real number. Then there is
![]() $p_0=p_0(\epsilon )$
and
$p_0=p_0(\epsilon )$
and
![]() $\delta =\delta (\epsilon )>0$
such that for any prime
$\delta =\delta (\epsilon )>0$
such that for any prime
![]() $p>p_0$
, any
$p>p_0$
, any
![]() $A, B \subseteq \mathbb {F}_p$
with
$A, B \subseteq \mathbb {F}_p$
with
![]() $|A|,|B|> p^{\epsilon }$
, and any non-trivial multiplicative character
$|A|,|B|> p^{\epsilon }$
, and any non-trivial multiplicative character
![]() $\chi $
of
$\chi $
of
![]() ${\mathbb F}_p$
, the following inequality holds:
${\mathbb F}_p$
, the following inequality holds:
 $$ \begin{align*} \bigg| \sum_{a\in A,\, b\in B} \chi(a+b)\bigg| \leq p^{-\delta} |A| |B|. \end{align*} $$
$$ \begin{align*} \bigg| \sum_{a\in A,\, b\in B} \chi(a+b)\bigg| \leq p^{-\delta} |A| |B|. \end{align*} $$
The connection between the Paley graph conjecture and the problem of bounding the size of Diophantine tuples was first observed by Güloğlu and Murty in [Reference Güloğlu and Murty16]. Let
![]() $d \geq 2$
be fixed,
$d \geq 2$
be fixed,
![]() $\lambda \in {\mathbb F}_p^*$
, where
$\lambda \in {\mathbb F}_p^*$
, where
![]() $p \equiv 1 \ \pmod d$
is a prime. The Paley graph conjecture trivially implies
$p \equiv 1 \ \pmod d$
is a prime. The Paley graph conjecture trivially implies
![]() $MD_{d}(\lambda , {\mathbb F}_p)=p^{o(1)}$
and
$MD_{d}(\lambda , {\mathbb F}_p)=p^{o(1)}$
and
![]() $MSD_{d}(\lambda , {\mathbb F}_p)=p^{o(1)}$
as
$MSD_{d}(\lambda , {\mathbb F}_p)=p^{o(1)}$
as
![]() $p \to \infty $
. Also, the bound on
$p \to \infty $
. Also, the bound on
![]() $M_k(n)$
in Theorem 1.2 can be improved to
$M_k(n)$
in Theorem 1.2 can be improved to
![]() $(\log n)^{o(1)}$
(see [Reference Dixit, Kim and Murty7], [Reference Güloğlu and Murty16]) when k is fixed and
$(\log n)^{o(1)}$
(see [Reference Dixit, Kim and Murty7], [Reference Güloğlu and Murty16]) when k is fixed and
![]() $n \to \infty $
. Furthermore, the Paley graph conjecture also immediately implies Sárközy’s conjecture (Conjecture 1.8) in view of Proposition 3.4. However, the Paley graph conjecture itself remains widely open, and our results are unconditional. We refer to [Reference Schoen and Shkredov32] and the references therein for recent progress on the Paley graph conjecture assuming
$n \to \infty $
. Furthermore, the Paley graph conjecture also immediately implies Sárközy’s conjecture (Conjecture 1.8) in view of Proposition 3.4. However, the Paley graph conjecture itself remains widely open, and our results are unconditional. We refer to [Reference Schoen and Shkredov32] and the references therein for recent progress on the Paley graph conjecture assuming
![]() $A,B$
have small doubling.
$A,B$
have small doubling.
3 Preliminary estimations for product sets in shifted multiplicative subgroups
3.1 Character sum estimate and the square root upper bound
The purpose of this subsection is to prove Proposition 1.4 by establishing an upper bound on the double character sum in Proposition 3.1 using basic properties of characters and Gauss sums. For any prime p, and any
![]() $x \in {\mathbb F}_p$
, we follow the standard notation that
$x \in {\mathbb F}_p$
, we follow the standard notation that
![]() $e_p(x)=\exp (2 \pi i x/p)$
, where we embed
$e_p(x)=\exp (2 \pi i x/p)$
, where we embed
![]() ${\mathbb F}_p$
into
${\mathbb F}_p$
into
![]() ${\mathbb Z}$
. We refer the reader to [Reference Lidl and Niederreiter26, Chapter 5] for more results related to Gauss sums and character sums.
${\mathbb Z}$
. We refer the reader to [Reference Lidl and Niederreiter26, Chapter 5] for more results related to Gauss sums and character sums.
We refer to [Reference Becker and Murty1, Section 2] for a historical discussion of Vinogradov’s inequality (1.1). Gyarmati [Reference Gyarmati17, Theorem 7] and Becker and Murty [Reference Becker and Murty1, Proposition 2.7] independently showed that the Legendre symbol in inequality (1.1) can be replaced with any non-trivial Dirichlet character modulo p. For our purposes, we extend Vinogradov’s inequality (1.1) to all finite fields
![]() ${\mathbb F}_q$
and all nontrivial multiplicative characters
${\mathbb F}_q$
and all nontrivial multiplicative characters
![]() $\chi $
of
$\chi $
of
![]() ${\mathbb F}_q$
, with a slightly improved upper bound.
${\mathbb F}_q$
, with a slightly improved upper bound.
Proposition 3.1 Let
![]() $\chi $
be a non-trivial multiplicative character of
$\chi $
be a non-trivial multiplicative character of
![]() ${\mathbb F}_q$
and
${\mathbb F}_q$
and
![]() $\lambda \in {\mathbb F}_q^*$
. For any
$\lambda \in {\mathbb F}_q^*$
. For any
![]() $A,B \subset {\mathbb F}_q^*$
, we have
$A,B \subset {\mathbb F}_q^*$
, we have
 $$ \begin{align*}\bigg|\sum_{a\in A,\, b\in B}\chi(ab+\lambda)\bigg| \leq \sqrt{q|A||B|}\bigg(1-\frac{\max\{|A|,|B|\}}{q}\bigg)^{1/2}. \end{align*} $$
$$ \begin{align*}\bigg|\sum_{a\in A,\, b\in B}\chi(ab+\lambda)\bigg| \leq \sqrt{q|A||B|}\bigg(1-\frac{\max\{|A|,|B|\}}{q}\bigg)^{1/2}. \end{align*} $$
Before proving Proposition 3.1, we need some preliminary estimates. Let
![]() $\chi $
be a multiplicative character of
$\chi $
be a multiplicative character of
![]() ${\mathbb F}_q$
; then the Gauss sum associated with
${\mathbb F}_q$
; then the Gauss sum associated with
![]() $\chi $
is defined to be
$\chi $
is defined to be
where
![]() $\operatorname {Tr}_{{\mathbb F}_q}:{\mathbb F}_q \to {\mathbb F}_p$
is the absolute trace map.
$\operatorname {Tr}_{{\mathbb F}_q}:{\mathbb F}_q \to {\mathbb F}_p$
is the absolute trace map.
Lemma 3.2 [Reference Lidl and Niederreiter26, Theorem 5.12]
Let
![]() $\chi $
be a multiplicative character of
$\chi $
be a multiplicative character of
![]() ${\mathbb F}_q$
. Then for any
${\mathbb F}_q$
. Then for any
![]() $a \in {\mathbb F}_q$
,
$a \in {\mathbb F}_q$
,
 $$ \begin{align*}\overline{\chi(a)}=\frac{1}{G(\chi)} \sum_{ c \in {\mathbb F}_q} \chi(c) e_p\big(\operatorname{Tr}_{{\mathbb F}_q}(ac)\big). \end{align*} $$
$$ \begin{align*}\overline{\chi(a)}=\frac{1}{G(\chi)} \sum_{ c \in {\mathbb F}_q} \chi(c) e_p\big(\operatorname{Tr}_{{\mathbb F}_q}(ac)\big). \end{align*} $$
Now we are ready to prove Proposition 3.1.
Proof of 3.1
By Lemma 3.2, we can write
 $$ \begin{align*} \sum_{a\in A,\, b\in B}\overline{\chi(ab+\lambda)} &=\sum_{a\in A,\, b\in B}\overline{\chi(b)} \overline{\chi(a+\lambda b^{-1})}\\ &=\frac{1}{G(\chi)} \sum_{c \in {\mathbb F}_q} \chi(c) \sum_{a\in A,\, b\in B} \overline{\chi(b)} e_p\big(\operatorname{Tr}((a+\lambda b^{-1})c)\big). \end{align*} $$
$$ \begin{align*} \sum_{a\in A,\, b\in B}\overline{\chi(ab+\lambda)} &=\sum_{a\in A,\, b\in B}\overline{\chi(b)} \overline{\chi(a+\lambda b^{-1})}\\ &=\frac{1}{G(\chi)} \sum_{c \in {\mathbb F}_q} \chi(c) \sum_{a\in A,\, b\in B} \overline{\chi(b)} e_p\big(\operatorname{Tr}((a+\lambda b^{-1})c)\big). \end{align*} $$
It is well-known that
![]() $|G(\chi )|= \sqrt {q}$
(see for example [Reference Lidl and Niederreiter26, Theorem 5.11]). Since
$|G(\chi )|= \sqrt {q}$
(see for example [Reference Lidl and Niederreiter26, Theorem 5.11]). Since
![]() $|\chi (c)|=1$
for each
$|\chi (c)|=1$
for each
![]() $c \in {\mathbb F}_q^*$
, we can apply the triangle inequality and Cauchy–Schwarz inequality to obtain
$c \in {\mathbb F}_q^*$
, we can apply the triangle inequality and Cauchy–Schwarz inequality to obtain
 $$ \begin{align*} &\bigg|\sum_{a\in A,\, b\in B}\chi(ab+\lambda)\bigg| \\ &\quad \leq \frac{1}{\sqrt{q}} \sum_{c \in {\mathbb F}_q^*} \bigg|\sum_{a\in A,\, b\in B} \overline{\chi(b)} e_p\big(\operatorname{Tr}((a+\lambda b^{-1})c)\big)\bigg|\\ &\quad \leq \frac{1}{\sqrt{q}} \bigg(\sum_{c \in {\mathbb F}_q^*} \bigg|\sum_{a\in A} e_p\big(\operatorname{Tr}(ac)\big)\bigg|^2\bigg)^{1/2} \bigg(\sum_{c \in {\mathbb F}_q^*}\bigg|\sum_{b\in B} \overline{\chi(b)}e_p\big(\operatorname{Tr}(b^{-1}c)\big)\bigg|^2\bigg)^{1/2}.\end{align*} $$
$$ \begin{align*} &\bigg|\sum_{a\in A,\, b\in B}\chi(ab+\lambda)\bigg| \\ &\quad \leq \frac{1}{\sqrt{q}} \sum_{c \in {\mathbb F}_q^*} \bigg|\sum_{a\in A,\, b\in B} \overline{\chi(b)} e_p\big(\operatorname{Tr}((a+\lambda b^{-1})c)\big)\bigg|\\ &\quad \leq \frac{1}{\sqrt{q}} \bigg(\sum_{c \in {\mathbb F}_q^*} \bigg|\sum_{a\in A} e_p\big(\operatorname{Tr}(ac)\big)\bigg|^2\bigg)^{1/2} \bigg(\sum_{c \in {\mathbb F}_q^*}\bigg|\sum_{b\in B} \overline{\chi(b)}e_p\big(\operatorname{Tr}(b^{-1}c)\big)\bigg|^2\bigg)^{1/2}.\end{align*} $$
By orthogonality relations, we have
 $$ \begin{align*}\sum_{c \in {\mathbb F}_q^*} \bigg|\sum_{a\in A} e_p\big(\operatorname{Tr}(ac)\big)\bigg|^2=q|A|-|A|^2, \quad \sum_{c \in {\mathbb F}_q^*}\bigg|\sum_{b\in B} \overline{\chi(b)}e_p\big(\operatorname{Tr}(b^{-1}c)\big)\bigg|^2\leq q|B|. \end{align*} $$
$$ \begin{align*}\sum_{c \in {\mathbb F}_q^*} \bigg|\sum_{a\in A} e_p\big(\operatorname{Tr}(ac)\big)\bigg|^2=q|A|-|A|^2, \quad \sum_{c \in {\mathbb F}_q^*}\bigg|\sum_{b\in B} \overline{\chi(b)}e_p\big(\operatorname{Tr}(b^{-1}c)\big)\bigg|^2\leq q|B|. \end{align*} $$
Thus, we have
 $$ \begin{align*}\bigg|\sum_{a\in A,\, b\in B}\chi(ab+\lambda)\bigg| \leq \sqrt{q|A||B|}\bigg(1-\frac{|A|}{q}\bigg)^{1/2}. \end{align*} $$
$$ \begin{align*}\bigg|\sum_{a\in A,\, b\in B}\chi(ab+\lambda)\bigg| \leq \sqrt{q|A||B|}\bigg(1-\frac{|A|}{q}\bigg)^{1/2}. \end{align*} $$
By switching the roles of A and B, we obtain the required character sum estimate.
Let
![]() $d \mid (q-1)$
such that
$d \mid (q-1)$
such that
![]() $d \ge 2$
and denote
$d \ge 2$
and denote
![]() $S_{d}=\{x^d \colon x \in \mathbb {F}_{q}^{*}\}$
with order
$S_{d}=\{x^d \colon x \in \mathbb {F}_{q}^{*}\}$
with order
![]() $\frac {q-1}{d}$
. Then we prove Proposition 1.4.
$\frac {q-1}{d}$
. Then we prove Proposition 1.4.
Proof of Proposition 1.4
Let
![]() $\chi $
be a multiplicative character of order d.
$\chi $
be a multiplicative character of order d.
Let
![]() $A \subset {\mathbb F}_q^*$
with property
$A \subset {\mathbb F}_q^*$
with property
![]() $SD_d(\lambda , {\mathbb F}_q)$
, that is,
$SD_d(\lambda , {\mathbb F}_q)$
, that is,
![]() $AA+\lambda \subset S_d \cup \{0\}$
. Note that
$AA+\lambda \subset S_d \cup \{0\}$
. Note that
![]() $\chi (ab+\lambda )=1$
for each
$\chi (ab+\lambda )=1$
for each
![]() $a,b \in A$
, unless
$a,b \in A$
, unless
![]() $ab+\lambda =0$
. Note that given
$ab+\lambda =0$
. Note that given
![]() $a \in A$
, there is at most one
$a \in A$
, there is at most one
![]() $b \in A$
such that
$b \in A$
such that
![]() $ab+\lambda =0$
. Therefore, by Proposition 3.1, we have
$ab+\lambda =0$
. Therefore, by Proposition 3.1, we have
 $$ \begin{align*}|A|^2-|A|\leq \bigg|\sum_{a,b\in A}\chi(ab+\lambda)\bigg|\leq \sqrt{q} |A| \bigg(1-\frac{|A|}{q}\bigg)^{1/2}. \end{align*} $$
$$ \begin{align*}|A|^2-|A|\leq \bigg|\sum_{a,b\in A}\chi(ab+\lambda)\bigg|\leq \sqrt{q} |A| \bigg(1-\frac{|A|}{q}\bigg)^{1/2}. \end{align*} $$
It follows that
Next we work under the weaker assumption
![]() $A \hat {\times } A+\lambda \subset S_d \cup \{0\}$
. In this case, note that
$A \hat {\times } A+\lambda \subset S_d \cup \{0\}$
. In this case, note that
![]() $\chi (ab+\lambda )=1$
for each
$\chi (ab+\lambda )=1$
for each
![]() $a,b \in A$
such that
$a,b \in A$
such that
![]() $a\neq b$
, unless
$a\neq b$
, unless
![]() $ab+\lambda =0$
. Proposition 3.1 then implies that
$ab+\lambda =0$
. Proposition 3.1 then implies that
 $$ \begin{align*}|A|^2-3|A|\leq \bigg|\sum_{a,b\in A}\chi(ab+\lambda)\bigg|\leq \sqrt{q} |A| \bigg(1-\frac{|A|}{q}\bigg)^{1/2} \end{align*} $$
$$ \begin{align*}|A|^2-3|A|\leq \bigg|\sum_{a,b\in A}\chi(ab+\lambda)\bigg|\leq \sqrt{q} |A| \bigg(1-\frac{|A|}{q}\bigg)^{1/2} \end{align*} $$
and it follows that
![]() $|A|\leq \sqrt {q-\frac {11}{4}}+\frac {5}{2}$
.
$|A|\leq \sqrt {q-\frac {11}{4}}+\frac {5}{2}$
.
3.2 Estimates on
 $|A|$
and
$|A|$
and
 $|B|$
if
$|B|$
if
 $AB=(S_d-\lambda )\setminus \{0\}$
$AB=(S_d-\lambda )\setminus \{0\}$
Let
![]() $A,B \subset {\mathbb F}_q^*$
and
$A,B \subset {\mathbb F}_q^*$
and
![]() $\lambda \in {\mathbb F}_q^*$
. In this subsection, we provide several useful estimates on
$\lambda \in {\mathbb F}_q^*$
. In this subsection, we provide several useful estimates on
![]() $|A|$
and
$|A|$
and
![]() $|B|$
when
$|B|$
when
![]() $AB=(S_{d}-\lambda ) \setminus \{0\}$
, which will be used in Section 6.
$AB=(S_{d}-\lambda ) \setminus \{0\}$
, which will be used in Section 6.
We need to use the following lemma, due to Karatsuba [Reference Karatsuba23].
Lemma 3.3 Let
![]() $A,B \subset {\mathbb F}_q^*$
and
$A,B \subset {\mathbb F}_q^*$
and
![]() $\lambda \in {\mathbb F}_q^*$
. Then for any non-trivial multiplicative character
$\lambda \in {\mathbb F}_q^*$
. Then for any non-trivial multiplicative character
![]() $\chi $
of
$\chi $
of
![]() ${\mathbb F}_q$
and any positive integer
${\mathbb F}_q$
and any positive integer
![]() $\nu $
, we have
$\nu $
, we have
 $$ \begin{align*}\sum_{\substack{a\in A\\ b\in B}} \chi(ab+\lambda) \ll_{\nu} |A|^{(2\nu-1)/2\nu} (|B|^{1/2}q^{1/2\nu}+|B|q^{1/4\nu}). \end{align*} $$
$$ \begin{align*}\sum_{\substack{a\in A\\ b\in B}} \chi(ab+\lambda) \ll_{\nu} |A|^{(2\nu-1)/2\nu} (|B|^{1/2}q^{1/2\nu}+|B|q^{1/4\nu}). \end{align*} $$
The following proposition improves and generalizes [Reference Sárközy31, Theorem 1]. It also improves [Reference Shkredov33, Lemma 17] (see Remark 3.7).
Proposition 3.4 Let
![]() $\epsilon>0$
. Let
$\epsilon>0$
. Let
![]() $d \mid (q-1)$
such that
$d \mid (q-1)$
such that
![]() $2 \leq d \leq q^{1/2-\epsilon }$
and
$2 \leq d \leq q^{1/2-\epsilon }$
and
![]() $\lambda \in {\mathbb F}^*_q$
. If
$\lambda \in {\mathbb F}^*_q$
. If
![]() $AB=(S_d-\lambda )\setminus \{0\}$
for some
$AB=(S_d-\lambda )\setminus \{0\}$
for some
![]() $A,B \subset {\mathbb F}_q^*$
with
$A,B \subset {\mathbb F}_q^*$
with
![]() $|A|, |B| \geq 2$
, then
$|A|, |B| \geq 2$
, then
Proof Let
![]() $A, B \subset {\mathbb F}_q^*$
and
$A, B \subset {\mathbb F}_q^*$
and
![]() $\lambda \in {\mathbb F}_q^*$
such that
$\lambda \in {\mathbb F}_q^*$
such that
![]() $AB=(S_d-\lambda )\setminus \{0\}$
with
$AB=(S_d-\lambda )\setminus \{0\}$
with
![]() $|A|, |B|\geq 2$
. Without loss of generality, we assume that
$|A|, |B|\geq 2$
. Without loss of generality, we assume that
![]() $|A|\geq |B|$
. We first establish a weaker lower bound that
$|A|\geq |B|$
. We first establish a weaker lower bound that
![]() $|B|\gg q^{\epsilon /2}$
.
$|B|\gg q^{\epsilon /2}$
.
When
![]() $d=2$
, Sárközy [Reference Sárközy31] has shown that
$d=2$
, Sárközy [Reference Sárközy31] has shown that
![]() $|B|\gg \frac {\sqrt {q}}{3\log q}$
. While he only proved this estimate when
$|B|\gg \frac {\sqrt {q}}{3\log q}$
. While he only proved this estimate when
![]() $q=p$
is a prime [Reference Sárközy31, Theorem 1], it is clear that the same proof extends to all finite fields
$q=p$
is a prime [Reference Sárközy31, Theorem 1], it is clear that the same proof extends to all finite fields
![]() ${\mathbb F}_q$
.
${\mathbb F}_q$
.
Next, assume that
![]() $d \geq 3$
. Let
$d \geq 3$
. Let
![]() $B=\{b_1, b_2, \ldots , b_k\}$
and
$B=\{b_1, b_2, \ldots , b_k\}$
and
![]() $|B|=k$
. Since
$|B|=k$
. Since
![]() $AB \subset S_d-\lambda $
, we have
$AB \subset S_d-\lambda $
, we have
![]() $AB+\lambda \subset S_d$
. Let
$AB+\lambda \subset S_d$
. Let
![]() $\chi $
be a multiplicative character of
$\chi $
be a multiplicative character of
![]() ${\mathbb F}_q$
with order d. Then it follows that for each
${\mathbb F}_q$
with order d. Then it follows that for each
![]() $a \in A$
, we have
$a \in A$
, we have
![]() $\chi (a+\lambda b_i^{-1})=1/\chi (b_i)$
for each
$\chi (a+\lambda b_i^{-1})=1/\chi (b_i)$
for each
![]() $1 \leq i \leq k$
. Therefore, by a well-known consequence of Weil’s bound (see for example [Reference Lidl and Niederreiter26, Exercise 5.66]),
$1 \leq i \leq k$
. Therefore, by a well-known consequence of Weil’s bound (see for example [Reference Lidl and Niederreiter26, Exercise 5.66]),
 $$ \begin{align*}|A|\leq \frac{q}{d^k}+\bigg(k-1-\frac{k}{d}+\frac{1}{d^k}\bigg)\sqrt{q}+\frac{k}{d}< \frac{q}{d^k}+k\sqrt{q}. \end{align*} $$
$$ \begin{align*}|A|\leq \frac{q}{d^k}+\bigg(k-1-\frac{k}{d}+\frac{1}{d^k}\bigg)\sqrt{q}+\frac{k}{d}< \frac{q}{d^k}+k\sqrt{q}. \end{align*} $$
On the other hand, since
![]() $AB=(S_d-\lambda )\setminus \{0\}$
, we have
$AB=(S_d-\lambda )\setminus \{0\}$
, we have
Combining the above two inequalities, we obtain that
Since
![]() $d \geq 3$
, it follows that
$d \geq 3$
, it follows that
![]() $k^2\sqrt {q}\gg \frac {q}{d}$
and thus
$k^2\sqrt {q}\gg \frac {q}{d}$
and thus
 $$ \begin{align*}|B|=k \gg \frac{q^{1/4}}{\sqrt{d}}\gg q^{\epsilon/2}. \end{align*} $$
$$ \begin{align*}|B|=k \gg \frac{q^{1/4}}{\sqrt{d}}\gg q^{\epsilon/2}. \end{align*} $$
Let
![]() $\nu =\lceil 2/\epsilon \rceil $
. By Lemma 3.3, and as
$\nu =\lceil 2/\epsilon \rceil $
. By Lemma 3.3, and as
![]() $|B| \gg q^{1/\nu }$
, we have
$|B| \gg q^{1/\nu }$
, we have
 $$ \begin{align*}|A||B|=\sum_{\substack{a\in A\\ b\in B}} \chi(ab+\lambda) \ll |A|^{(2\nu-1)/2\nu} (|B|^{1/2}q^{1/2\nu}+|B|q^{1/4\nu})\ll |A|^{(2\nu-1)/2\nu}|B|q^{1/4\nu}. \end{align*} $$
$$ \begin{align*}|A||B|=\sum_{\substack{a\in A\\ b\in B}} \chi(ab+\lambda) \ll |A|^{(2\nu-1)/2\nu} (|B|^{1/2}q^{1/2\nu}+|B|q^{1/4\nu})\ll |A|^{(2\nu-1)/2\nu}|B|q^{1/4\nu}. \end{align*} $$
It follows that
![]() $|A|\ll q^{1/2}$
. Thus,
$|A|\ll q^{1/2}$
. Thus,
![]() $|B|\gg |S_d|/|A|\gg q^{1/2}/d$
.
$|B|\gg |S_d|/|A|\gg q^{1/2}/d$
.
Remark 3.5 We remark that the same method could be used to refine a similar result for the additive decomposition of multiplicative subgroups, which improves a result of Shparlinski [Reference Shparlinski34, Theorem 6.1] (moreover, our proof appears to be much simpler than his proof). More precisely, we can prove the following:
Let
![]() $\epsilon>0$
. Let
$\epsilon>0$
. Let
![]() $d \mid (q-1)$
such that
$d \mid (q-1)$
such that
![]() $2 \leq d \leq q^{1/2-\epsilon }$
. If
$2 \leq d \leq q^{1/2-\epsilon }$
. If
![]() $A+B=S_d$
for some
$A+B=S_d$
for some
![]() $A,B \subset {\mathbb F}_q$
with
$A,B \subset {\mathbb F}_q$
with
![]() $|A|, |B| \geq 2$
, then
$|A|, |B| \geq 2$
, then
Note that Proposition 3.4 only applies to multiplicative subgroups
![]() $G=S_d$
with
$G=S_d$
with
![]() $|G|>\sqrt {q}$
. When
$|G|>\sqrt {q}$
. When
![]() $q=p$
is a prime, and G is a non-trivial multiplicative subgroup of
$q=p$
is a prime, and G is a non-trivial multiplicative subgroup of
![]() ${\mathbb F}_p$
(in particular,
${\mathbb F}_p$
(in particular,
![]() $|G|<\sqrt {p}$
is allowed), we have the following estimate, due to Shkredov [Reference Shkredov33].
$|G|<\sqrt {p}$
is allowed), we have the following estimate, due to Shkredov [Reference Shkredov33].
Lemma 3.6 If G is a proper multiplicative subgroup of
![]() ${\mathbb F}_p$
such that
${\mathbb F}_p$
such that
![]() $AB=(G-\lambda )\setminus \{0\}$
for some
$AB=(G-\lambda )\setminus \{0\}$
for some
![]() $A,B \subset {\mathbb F}_p^*$
with
$A,B \subset {\mathbb F}_p^*$
with
![]() $|A|,|B| \geq 2$
and some
$|A|,|B| \geq 2$
and some
![]() $\lambda \in {\mathbb F}_p^*$
, then
$\lambda \in {\mathbb F}_p^*$
, then
as
![]() $|G| \to \infty $
.
$|G| \to \infty $
.
Proof If
![]() $0 \in G-\lambda $
, let
$0 \in G-\lambda $
, let
![]() $A'=A \cup \{0\}$
; otherwise, let
$A'=A \cup \{0\}$
; otherwise, let
![]() $A'=A$
. Then we have
$A'=A$
. Then we have
![]() $A'B=G-\lambda $
, or equivalently,
$A'B=G-\lambda $
, or equivalently,
![]() $A'/(B^{-1})=G-\lambda $
. Note that
$A'/(B^{-1})=G-\lambda $
. Note that
![]() $|A' \setminus \{0\}|=|A|\geq 2$
and
$|A' \setminus \{0\}|=|A|\geq 2$
and
![]() $|B^{-1}|=|B| \geq 2$
, thus, the lemma then follows immediately from [Reference Shkredov33, Lemma 17].
$|B^{-1}|=|B| \geq 2$
, thus, the lemma then follows immediately from [Reference Shkredov33, Lemma 17].
Remark 3.7 Let
![]() $AB=(S_d-\lambda ) \setminus \{0\}$
, where
$AB=(S_d-\lambda ) \setminus \{0\}$
, where
![]() $A,B \subset {\mathbb F}_p^*$
with
$A,B \subset {\mathbb F}_p^*$
with
![]() $|A|, |B| \geq 2$
and
$|A|, |B| \geq 2$
and
![]() $\lambda \in {\mathbb F}_p^*$
. When d is a constant, and
$\lambda \in {\mathbb F}_p^*$
. When d is a constant, and
![]() $p \to \infty $
, Proposition 3.4 is better than Lemma 3.6. Indeed, in [Reference Shkredov33, Lemma 17], Shkredov showed that
$p \to \infty $
, Proposition 3.4 is better than Lemma 3.6. Indeed, in [Reference Shkredov33, Lemma 17], Shkredov showed that
![]() $\max \{|A|, |B|\} \ll \sqrt {p}\log p$
, while Proposition 3.4 showed the stronger result that
$\max \{|A|, |B|\} \ll \sqrt {p}\log p$
, while Proposition 3.4 showed the stronger result that
![]() $\max \{|A|, |B|\} \ll \sqrt {p}$
, removing the
$\max \{|A|, |B|\} \ll \sqrt {p}$
, removing the
![]() $\log p$
factor. This stronger bound would be crucial in proving results related to multiplicative decompositions (for example, Theorem 6.1). Instead, Lemma 3.6 will be useful for applications in ternary decompositions (Theorem 6.6).
$\log p$
factor. This stronger bound would be crucial in proving results related to multiplicative decompositions (for example, Theorem 6.1). Instead, Lemma 3.6 will be useful for applications in ternary decompositions (Theorem 6.6).
Remark 3.8 Lemma 3.6 fails to extend to
![]() ${\mathbb F}_q$
, where q is a proper prime power. Let
${\mathbb F}_q$
, where q is a proper prime power. Let
![]() $q=r^2$
be a square,
$q=r^2$
be a square,
![]() $G={\mathbb F}_r^*$
, and
$G={\mathbb F}_r^*$
, and
![]() $\lambda =-1$
. Let A be a subset of
$\lambda =-1$
. Let A be a subset of
![]() ${\mathbb F}_r^*$
with size
${\mathbb F}_r^*$
with size
![]() $\lfloor (r-1)/2 \rfloor $
. Let
$\lfloor (r-1)/2 \rfloor $
. Let
![]() $B={\mathbb F}_r^* \setminus A^{-1}$
. Then we have
$B={\mathbb F}_r^* \setminus A^{-1}$
. Then we have
![]() $AB={\mathbb F}_r^* \setminus \{1\}=(G+1)\setminus \{0\}$
while
$AB={\mathbb F}_r^* \setminus \{1\}=(G+1)\setminus \{0\}$
while
![]() $|A|, |B| \gg |G|$
.
$|A|, |B| \gg |G|$
.
Remark 3.9 Let
![]() $d \geq 2$
be fixed. Let
$d \geq 2$
be fixed. Let
![]() $q \equiv 1 \ \pmod d$
be a prime power and let
$q \equiv 1 \ \pmod d$
be a prime power and let
![]() $\lambda \in {\mathbb F}_{q}^*$
, we define
$\lambda \in {\mathbb F}_{q}^*$
, we define
![]() $N(q,\lambda )$
be the total number of pairs
$N(q,\lambda )$
be the total number of pairs
![]() $(A,B)$
of sets
$(A,B)$
of sets
![]() $A,B \subseteq \mathbb {F}_{q}$
with
$A,B \subseteq \mathbb {F}_{q}$
with
![]() $|A|, |B| \geq 2$
such that
$|A|, |B| \geq 2$
such that
![]() $AB = (S_{d} - \lambda ) \setminus \{0 \}$
. Note that Conjecture 1.9 implies
$AB = (S_{d} - \lambda ) \setminus \{0 \}$
. Note that Conjecture 1.9 implies
![]() $N(q,\lambda )=0$
when q is sufficiently large, but it seems out of reach in general. Instead, one can find a non-trivial upper bound of
$N(q,\lambda )=0$
when q is sufficiently large, but it seems out of reach in general. Instead, one can find a non-trivial upper bound of
![]() $N(q,\lambda )$
. Using Proposition 3.4 and following the same strategy of the proof in [Reference Blackburn, Konyagin and Shparlinski3, Theorem 1], we have a non-trivial upper bound of
$N(q,\lambda )$
. Using Proposition 3.4 and following the same strategy of the proof in [Reference Blackburn, Konyagin and Shparlinski3, Theorem 1], we have a non-trivial upper bound of
![]() $N(q,\lambda )$
as follows:
$N(q,\lambda )$
as follows:
We also note that by using Corollary 1.10, we confirmed
![]() $N(q, \lambda )=0$
if q is a prime,
$N(q, \lambda )=0$
if q is a prime,
![]() $\lambda \in S_{d}$
, and
$\lambda \in S_{d}$
, and
![]() $|S_d|-1$
is a prime. In addition, Theorem 1.11 gives the same result for
$|S_d|-1$
is a prime. In addition, Theorem 1.11 gives the same result for
![]() $N(p,n)$
asymptotically for a subset of primes p with lower density at least
$N(p,n)$
asymptotically for a subset of primes p with lower density at least
![]() $\frac {1}{[\mathbb {Q}(e^{2\pi i/d}, n^{1/d}):\mathbb {Q}]}$
.
$\frac {1}{[\mathbb {Q}(e^{2\pi i/d}, n^{1/d}):\mathbb {Q}]}$
.
4 Products and restricted products in shifted multiplicative subgroups
In this section, we use Stepanov’s method to study product sets and restricted product sets that are contained in shifted multiplicative subgroups. Our proofs are inspired by Stepanov’s original paper [Reference Stepanov35], and the recent breakthrough of Hanson and Pertidis [Reference Hanson and Petridis21], together with its extensions and applications developed by the second author [Reference Yip38, Reference Yip40].
Throughout the section, we assume
![]() $d \geq 2$
and
$d \geq 2$
and
![]() $q \equiv 1 \ \pmod d$
is a prime power. Recall that
$q \equiv 1 \ \pmod d$
is a prime power. Recall that
![]() $S_d=S_d({\mathbb F}_q)=\{x^d: x \in {\mathbb F}_q^*\}$
.
$S_d=S_d({\mathbb F}_q)=\{x^d: x \in {\mathbb F}_q^*\}$
.
4.1 Product set in a shifted multiplicative subgroup
In this subsection, we prove Theorem 1.1, which can be viewed as the bipartite version of Diophantine tuples over finite fields. As a corollary of Theorem 1.1, we prove Corollary 1.10. Besides it, Theorem 1.1 will be also repeatedly used to prove several of our main results in the present article.
Proof of Theorem 1.1
Let
![]() $r=|B \cap (-\lambda A^{-1})|$
. Let
$r=|B \cap (-\lambda A^{-1})|$
. Let
![]() $A=\{a_1,a_2,\ldots , a_n\}$
and
$A=\{a_1,a_2,\ldots , a_n\}$
and
![]() $B=\{b_1,b_2, \ldots , b_m\}$
such that
$B=\{b_1,b_2, \ldots , b_m\}$
such that
![]() $b_{r+1}, \ldots , b_m \notin (-\lambda A^{-1})$
. Since
$b_{r+1}, \ldots , b_m \notin (-\lambda A^{-1})$
. Since
![]() $AB+\lambda \subset S_d \cup \{0\}$
, we have
$AB+\lambda \subset S_d \cup \{0\}$
, we have
for each
![]() $1 \leq i \leq n$
and
$1 \leq i \leq n$
and
![]() $1 \leq j \leq m$
. This simple observation will be used repeatedly in the following computation.
$1 \leq j \leq m$
. This simple observation will be used repeatedly in the following computation.
Let
![]() $c_1,c_2,...,c_n \in {\mathbb F}_q$
be the unique solution of the following system of equations:
$c_1,c_2,...,c_n \in {\mathbb F}_q$
be the unique solution of the following system of equations:

This is justified by the invertibility of the coefficient matrix of the system (a Vandermonde matrix). We claim that
![]() $\sum _{i=1}^n c_ia_i^n\neq 0$
. Suppose otherwise that
$\sum _{i=1}^n c_ia_i^n\neq 0$
. Suppose otherwise that
![]() $\sum _{i=1}^n c_ia_i^n=0$
, then
$\sum _{i=1}^n c_ia_i^n=0$
, then
![]() $c_i=0$
for all i, violating the assumption
$c_i=0$
for all i, violating the assumption
![]() $\sum _{i=1}^n c_i=1$
in equation (4.1). Indeed, the generalized Vandermonde matrix
$\sum _{i=1}^n c_i=1$
in equation (4.1). Indeed, the generalized Vandermonde matrix
![]() $(a_i^j)_{1 \leq i \leq n, 1 \leq j \leq n}$
is non-singular since it has determinant
$(a_i^j)_{1 \leq i \leq n, 1 \leq j \leq n}$
is non-singular since it has determinant
Consider the following auxiliary polynomial
 $$ \begin{align} f(x)=-\lambda^{n-1}+\sum_{i=1}^n c_i (a_ix+\lambda)^{n-1+\frac{q-1}{d}}\in {\mathbb F}_q[x]. \end{align} $$
$$ \begin{align} f(x)=-\lambda^{n-1}+\sum_{i=1}^n c_i (a_ix+\lambda)^{n-1+\frac{q-1}{d}}\in {\mathbb F}_q[x]. \end{align} $$
Note that
![]() $n=|A| \leq |S_d \cup \{0\}|\leq \frac {q-1}{d}+1$
. Thus, if
$n=|A| \leq |S_d \cup \{0\}|\leq \frac {q-1}{d}+1$
. Thus, if
![]() $q=p$
is a prime, then
$q=p$
is a prime, then
![]() $n-1+\frac {p-1}{d} \leq \frac {2(p-1)}{d} \leq p-1$
and thus the condition
$n-1+\frac {p-1}{d} \leq \frac {2(p-1)}{d} \leq p-1$
and thus the condition
![]() $\binom {n-1+\frac {q-1}{d}}{n} \not \equiv 0 \ \pmod p$
is automatically satisfied. Then f is a non-zero polynomial since the coefficient of
$\binom {n-1+\frac {q-1}{d}}{n} \not \equiv 0 \ \pmod p$
is automatically satisfied. Then f is a non-zero polynomial since the coefficient of
![]() $x^n$
in f is
$x^n$
in f is
 $$ \begin{align*}\binom{n-1+\frac{q-1}{d}}{n} \cdot \lambda^{\frac{q-1}{d}-1} \cdot \sum_{i=1}^n c_i a_i^n \neq 0 \end{align*} $$
$$ \begin{align*}\binom{n-1+\frac{q-1}{d}}{n} \cdot \lambda^{\frac{q-1}{d}-1} \cdot \sum_{i=1}^n c_i a_i^n \neq 0 \end{align*} $$
by the assumption on the binomial coefficient. Also, it is clear that the degree of f is at most
![]() $n-1+\frac {q-1}{d}$
.
$n-1+\frac {q-1}{d}$
.
Next, we compute the derivatives of f on B. For each
![]() $1\leq j \leq m$
, system (4.1) implies that
$1\leq j \leq m$
, system (4.1) implies that
 $$ \begin{align*} E^{(0)} f (b_j) &= -\lambda^{n-1}+\sum_{i=1}^n c_i (a_ib_j+\lambda)^{n-1} \\ &= -\lambda^{n-1}+\sum_{\ell=0}^{n-1} \binom{n-1}{\ell} \lambda^{n-1-\ell}\bigg(\sum_{i=1}^n c_i a_i^\ell\bigg)b_j^{\ell} =0. \end{align*} $$
$$ \begin{align*} E^{(0)} f (b_j) &= -\lambda^{n-1}+\sum_{i=1}^n c_i (a_ib_j+\lambda)^{n-1} \\ &= -\lambda^{n-1}+\sum_{\ell=0}^{n-1} \binom{n-1}{\ell} \lambda^{n-1-\ell}\bigg(\sum_{i=1}^n c_i a_i^\ell\bigg)b_j^{\ell} =0. \end{align*} $$
For each
![]() $1\leq j \leq m$
and
$1\leq j \leq m$
and
![]() $1 \leq k \leq n-2$
, we have that
$1 \leq k \leq n-2$
, we have that
 $$ \begin{align*} E^{(k)} f (b_j) &= \binom{n-1+\frac{q-1}{d}}{k} \sum_{i=1}^n c_i a_i^k (a_ib_j+\lambda)^{n-1+\frac{q-1}{d}-k} \\ &= \binom{n-1+\frac{q-1}{d}}{k} \sum_{i=1}^n c_i a_i^k (a_ib_j+\lambda)^{n-1-k} \\ &= \binom{n-1+\frac{q-1}{d}}{k} \sum_{\ell=0}^{n-1-k} \binom{n-1-k}{\ell} \lambda^{n-1-k-\ell} \bigg(\sum_{i=1}^n c_i a_i^{k+\ell}\bigg)b_j^{\ell} =0, \end{align*} $$
$$ \begin{align*} E^{(k)} f (b_j) &= \binom{n-1+\frac{q-1}{d}}{k} \sum_{i=1}^n c_i a_i^k (a_ib_j+\lambda)^{n-1+\frac{q-1}{d}-k} \\ &= \binom{n-1+\frac{q-1}{d}}{k} \sum_{i=1}^n c_i a_i^k (a_ib_j+\lambda)^{n-1-k} \\ &= \binom{n-1+\frac{q-1}{d}}{k} \sum_{\ell=0}^{n-1-k} \binom{n-1-k}{\ell} \lambda^{n-1-k-\ell} \bigg(\sum_{i=1}^n c_i a_i^{k+\ell}\bigg)b_j^{\ell} =0, \end{align*} $$
where we use Lemma 2.3 and the assumptions in system (4.1).
For each
![]() $r+1\leq j \leq m$
, by the assumption,
$r+1\leq j \leq m$
, by the assumption,
![]() $b_j \notin (-\lambda A^{-1})$
, that is,
$b_j \notin (-\lambda A^{-1})$
, that is,
![]() $a_ib_j+\lambda \neq 0$
for each
$a_ib_j+\lambda \neq 0$
for each
![]() $1 \leq i \leq n$
. Thus, for each
$1 \leq i \leq n$
. Thus, for each
![]() $r+1\leq j \leq m$
, we additionally have
$r+1\leq j \leq m$
, we additionally have
 $$ \begin{align*} E^{(n-1)} f (b_j) &= \binom{n-1+\frac{q-1}{d}}{n-1} \sum_{i=1}^n c_i a_i^{n-1}(a_ib_j+\lambda)^{\frac{q-1}{d}} = \binom{n-1+\frac{q-1}{d}}{n-1} \sum_{i=1}^n c_i a_i^{n-1}=0. \end{align*} $$
$$ \begin{align*} E^{(n-1)} f (b_j) &= \binom{n-1+\frac{q-1}{d}}{n-1} \sum_{i=1}^n c_i a_i^{n-1}(a_ib_j+\lambda)^{\frac{q-1}{d}} = \binom{n-1+\frac{q-1}{d}}{n-1} \sum_{i=1}^n c_i a_i^{n-1}=0. \end{align*} $$
Therefore, Lemma 2.4 allows us to conclude that each of
![]() $b_1,b_2, \ldots b_r$
is a root of f with multiplicity at least
$b_1,b_2, \ldots b_r$
is a root of f with multiplicity at least
![]() $n-1$
, and each of
$n-1$
, and each of
![]() $b_{r+1},b_{r+2}, \ldots b_m$
is a root of f with multiplicity at least n. It follows that
$b_{r+1},b_{r+2}, \ldots b_m$
is a root of f with multiplicity at least n. It follows that
Finally, assuming that
![]() $\lambda \in S_d$
. In this case,
$\lambda \in S_d$
. In this case,
 $$ \begin{align*}f(0)=-\lambda^{n-1}+\lambda^{n-1+\frac{q-1}{d}}\sum_{i=1}^n c_i=-\lambda^{n-1}+\lambda^{n-1}=0. \end{align*} $$
$$ \begin{align*}f(0)=-\lambda^{n-1}+\lambda^{n-1+\frac{q-1}{d}}\sum_{i=1}^n c_i=-\lambda^{n-1}+\lambda^{n-1}=0. \end{align*} $$
And the coefficient of
![]() $x^j$
of f is
$x^j$
of f is
![]() $0$
for each
$0$
for each
![]() $1 \leq j \leq n-1$
by the assumptions on
$1 \leq j \leq n-1$
by the assumptions on
![]() $c_i$
’s. It follows that
$c_i$
’s. It follows that
![]() $0$
is also a root of f with multiplicity n. Since
$0$
is also a root of f with multiplicity n. Since
![]() $0 \notin B$
, we have the stronger estimate that
$0 \notin B$
, we have the stronger estimate that
![]() $mn-r+n\leq \frac {q-1}{d}+n-1.$
$mn-r+n\leq \frac {q-1}{d}+n-1.$
Remark 4.1 More generally, one can study the same question if
![]() $AB+\lambda $
is instead contained in a coset of
$AB+\lambda $
is instead contained in a coset of
![]() $S_d$
. However, note that this more general case can be always reduced to the special case studied in Theorem 1.1. Indeed, if
$S_d$
. However, note that this more general case can be always reduced to the special case studied in Theorem 1.1. Indeed, if
![]() $AB+\lambda \subset \xi S_d \cup \{0\}$
with
$AB+\lambda \subset \xi S_d \cup \{0\}$
with
![]() $\xi \in {\mathbb F}_q^*$
, then
$\xi \in {\mathbb F}_q^*$
, then
![]() $A'B+\lambda /\xi \subset S_d \cup \{0\}$
, where
$A'B+\lambda /\xi \subset S_d \cup \{0\}$
, where
![]() $A'=A/\xi $
.
$A'=A/\xi $
.
Next, we prove Corollary 1.10, an important corollary of Theorem 1.1. It would be crucial for proving results in Section 6.
Proof of Corollary 1.10
Since
![]() $0 \notin AB+\lambda $
, we have
$0 \notin AB+\lambda $
, we have
![]() $B \cap (-\lambda A^{-1})=\emptyset $
, thus Theorem 1.1 implies that
$B \cap (-\lambda A^{-1})=\emptyset $
, thus Theorem 1.1 implies that
![]() $|A||B| \leq |S_d|-1$
. On the other hand, since
$|A||B| \leq |S_d|-1$
. On the other hand, since
![]() $(S_d-\lambda ) \setminus \{0\}=AB$
, it follows that
$(S_d-\lambda ) \setminus \{0\}=AB$
, it follows that
![]() $|A||B| \geq |AB|=|(S_d-\lambda ) \setminus \{0\}|=|S_d|-1$
. Therefore, we have
$|A||B| \geq |AB|=|(S_d-\lambda ) \setminus \{0\}|=|S_d|-1$
. Therefore, we have
![]() $|A||B|=|AB|=|S_d|-1$
.
$|A||B|=|AB|=|S_d|-1$
.
4.2 Restricted product set in a shifted multiplicative subgroup
Recall that
![]() $A' \subset {\mathbb F}_q^*$
has property
$A' \subset {\mathbb F}_q^*$
has property
![]() $D_d(\lambda , {\mathbb F}_q)$
if and only if
$D_d(\lambda , {\mathbb F}_q)$
if and only if
![]() $ab+\lambda \in S_d \cup \{0\}$
for each
$ab+\lambda \in S_d \cup \{0\}$
for each
![]() $a,b \in A'$
such that
$a,b \in A'$
such that
![]() $a \neq b$
. In other words,
$a \neq b$
. In other words,
![]() $A' \hat {\times } A'+\lambda \subset S_d \cup \{0\}$
. Thus, in this subsection, we are led to study restricted product sets and we establish the following restricted product analog of Theorem 1.1. In the next subsection, Theorems 1.1 and 4.2 will be applied together to prove Theorem 1.5 in the case that q is a prime and Theorem 1.6 in the case that q is a square.
$A' \hat {\times } A'+\lambda \subset S_d \cup \{0\}$
. Thus, in this subsection, we are led to study restricted product sets and we establish the following restricted product analog of Theorem 1.1. In the next subsection, Theorems 1.1 and 4.2 will be applied together to prove Theorem 1.5 in the case that q is a prime and Theorem 1.6 in the case that q is a square.
Theorem 4.2 Let
![]() $d \geq 2$
and let
$d \geq 2$
and let
![]() $q \equiv 1 \ \pmod d$
be a prime power. Let
$q \equiv 1 \ \pmod d$
be a prime power. Let
![]() $A' \subset {\mathbb F}_q^*$
and
$A' \subset {\mathbb F}_q^*$
and
![]() $\lambda \in {\mathbb F}_q^*$
. If
$\lambda \in {\mathbb F}_q^*$
. If
![]() $A' \hat {\times } A'+\lambda \subset S_d \cup \{0\}$
while
$A' \hat {\times } A'+\lambda \subset S_d \cup \{0\}$
while
![]() $A'A'+\lambda \not \subset S_d \cup \{0\}$
, then
$A'A'+\lambda \not \subset S_d \cup \{0\}$
, then
![]() $|A'|\leq \sqrt {2(q-1)/d}+4$
.
$|A'|\leq \sqrt {2(q-1)/d}+4$
.
The proof of Theorem 4.2 is similar to Theorem 1.1, but it is more delicate. In particular, the choice of the auxiliary polynomial (4.4) needs to be modified from that of the proof (4.2) of Theorem 1.1. In view of Theorem 1.1, we can further assume that
![]() $A'A'+\lambda \not \subset S_d \cup \{0\}$
, for otherwise we already have a good bound on
$A'A'+\lambda \not \subset S_d \cup \{0\}$
, for otherwise we already have a good bound on
![]() $|A'|$
; we refer to Section 4.3 for details. It turns out that this additional assumption (which we get for free) is crucial in our proof since it guarantees that the auxiliary polynomial we constructed is not identically zero.
$|A'|$
; we refer to Section 4.3 for details. It turns out that this additional assumption (which we get for free) is crucial in our proof since it guarantees that the auxiliary polynomial we constructed is not identically zero.
Proof of Theorem 4.2
Since
![]() $A'A'+\lambda \not \subset S_d \cup \{0\}$
, there is
$A'A'+\lambda \not \subset S_d \cup \{0\}$
, there is
![]() $b \in A'$
such that
$b \in A'$
such that
![]() $b^2+\lambda \not \subset S_d \cup \{0\}$
. Let
$b^2+\lambda \not \subset S_d \cup \{0\}$
. Let
![]() $A"=A' \setminus \{-\lambda /b\}$
. If
$A"=A' \setminus \{-\lambda /b\}$
. If
![]() $|A"|=1$
, then we are done. Otherwise, if
$|A"|=1$
, then we are done. Otherwise, if
![]() $|A"|$
is even, let
$|A"|$
is even, let
![]() $A=A"$
; if
$A=A"$
; if
![]() $|A"|$
is odd, let
$|A"|$
is odd, let
![]() $A=A" \setminus \{b'\}$
, where
$A=A" \setminus \{b'\}$
, where
![]() $b' \in A"$
is an arbitrary element such that
$b' \in A"$
is an arbitrary element such that
![]() $b' \neq b$
. Then we have
$b' \neq b$
. Then we have
![]() $b \in A$
and
$b \in A$
and
![]() $|A|$
is even. Note that
$|A|$
is even. Note that
![]() $|A| \geq |A'|-2$
, thus it suffices to show
$|A| \geq |A'|-2$
, thus it suffices to show
![]() $|A|\leq \sqrt {2(q-1)/d}+2$
.
$|A|\leq \sqrt {2(q-1)/d}+2$
.
Let
![]() $|A|=n$
, where n is even. Write
$|A|=n$
, where n is even. Write
![]() $A=\{a_1, a_2, \ldots , a_n\}$
. Without loss of generality, we may assume that
$A=\{a_1, a_2, \ldots , a_n\}$
. Without loss of generality, we may assume that
![]() $a_1=b$
. Let
$a_1=b$
. Let
![]() $m=n/2-1$
. Let
$m=n/2-1$
. Let
![]() $c_1,c_2,...,c_n \in {\mathbb F}_q$
be the unique solution of the following system of equations:
$c_1,c_2,...,c_n \in {\mathbb F}_q$
be the unique solution of the following system of equations:

Indeed, that coefficient matrix of the system is the generalized Vandermonde matrix
![]() $(a_i^j)_{1 \leq i \leq n, -m \leq j \leq m+1},$
which is non-singular since it has nonzero determinant
$(a_i^j)_{1 \leq i \leq n, -m \leq j \leq m+1},$
which is non-singular since it has nonzero determinant
![]() $(a_1 a_2 \ldots a_n)^{-m} \prod _{i<j} (a_j-a_i)\neq 0.$
Note that
$(a_1 a_2 \ldots a_n)^{-m} \prod _{i<j} (a_j-a_i)\neq 0.$
Note that
![]() $c_1 \neq 0$
; for otherwise
$c_1 \neq 0$
; for otherwise
![]() $c_1=0$
and we must have
$c_1=0$
and we must have
![]() $c_1=c_2=\cdots =c_n=0$
in view of the first
$c_1=c_2=\cdots =c_n=0$
in view of the first
![]() $n-1$
equations in system (4.3), which contradicts the last equation in system (4.3).
$n-1$
equations in system (4.3), which contradicts the last equation in system (4.3).
Consider the following auxiliary polynomial
 $$ \begin{align} f(x)=\sum_{i=1}^n c_i (a_ix+\lambda)^{m+\frac{q-1}{d}} (a_i^{-1}x-1)^m\in {\mathbb F}_q[x]. \end{align} $$
$$ \begin{align} f(x)=\sum_{i=1}^n c_i (a_ix+\lambda)^{m+\frac{q-1}{d}} (a_i^{-1}x-1)^m\in {\mathbb F}_q[x]. \end{align} $$
It is clear that the degree of f is at most
![]() $2m+\frac {q-1}{d}$
. Since
$2m+\frac {q-1}{d}$
. Since
![]() $A \hat {\times } A+\lambda \subset S_d \cup \{0\}$
, we have
$A \hat {\times } A+\lambda \subset S_d \cup \{0\}$
, we have
for each
![]() $1 \leq i,j \leq n$
. This simple observation will be used repeatedly in the following computation.
$1 \leq i,j \leq n$
. This simple observation will be used repeatedly in the following computation.
First, we claim that for each
![]() $0 \leq k_1<m$
,
$0 \leq k_1<m$
,
![]() $0\leq k_2<m$
, and
$0\leq k_2<m$
, and
![]() $1 \leq j \leq n$
, we have
$1 \leq j \leq n$
, we have
 $$ \begin{align} \sum_{i=1}^n c_i E^{(k_1)}[(a_ix+\lambda)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(k_2)}[(a_i^{-1}x-1)^m](a_j)=0. \end{align} $$
$$ \begin{align} \sum_{i=1}^n c_i E^{(k_1)}[(a_ix+\lambda)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(k_2)}[(a_i^{-1}x-1)^m](a_j)=0. \end{align} $$
Indeed, by Lemma 2.3, we have
 $$ \begin{align*} &\sum_{i=1}^n c_i E^{(k_1)}[(a_ix+\lambda)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(k_2)}[(a_i^{-1}x-1)^m](a_j)\\ &\quad = \binom{m+\frac{q-1}{d}}{k_1} \binom{m}{k_2} \bigg(\sum_{i=1}^n c_i a_i^{k_1-k_2} (a_ja_i+\lambda)^{m-k_1} (a_i^{-1}a_j-1)^{m-k_2}\bigg) \\ &\quad = \binom{m+\frac{q-1}{d}}{k_1} \binom{m}{k_2} \sum_{\ell_1=0}^{m-k_1} \sum_{\ell_2=0}^{m-k_2} \binom{m-k_1}{\ell_1} \binom{m-k_2}{\ell_2} \\ &\qquad \times\bigg(\sum_{i=1}^n c_i a_i^{k_1-k_2} (a_ja_i)^{\ell_1} \lambda^{m-k_1-\ell_1} (a_i^{-1}a_j)^{\ell_2}(-1)^{m-k_2-\ell_2}\bigg)\\ &\quad = \binom{m+\frac{q-1}{d}}{k_1} \binom{m}{k_2} \sum_{\ell_1=0}^{m-k_1} \sum_{\ell_2=0}^{m-k_2} \binom{m-k_1}{\ell_1} \binom{m-k_2}{\ell_2} a_j^{\ell_1+\ell_2} \lambda^{m-k_1-\ell_1} (-1)^{m-k_2-\ell_2} \\ &\qquad \times \bigg(\sum_{i=1}^n c_i a_i^{(k_1+\ell_1)-(k_2+\ell_2)} \bigg). \end{align*} $$
$$ \begin{align*} &\sum_{i=1}^n c_i E^{(k_1)}[(a_ix+\lambda)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(k_2)}[(a_i^{-1}x-1)^m](a_j)\\ &\quad = \binom{m+\frac{q-1}{d}}{k_1} \binom{m}{k_2} \bigg(\sum_{i=1}^n c_i a_i^{k_1-k_2} (a_ja_i+\lambda)^{m-k_1} (a_i^{-1}a_j-1)^{m-k_2}\bigg) \\ &\quad = \binom{m+\frac{q-1}{d}}{k_1} \binom{m}{k_2} \sum_{\ell_1=0}^{m-k_1} \sum_{\ell_2=0}^{m-k_2} \binom{m-k_1}{\ell_1} \binom{m-k_2}{\ell_2} \\ &\qquad \times\bigg(\sum_{i=1}^n c_i a_i^{k_1-k_2} (a_ja_i)^{\ell_1} \lambda^{m-k_1-\ell_1} (a_i^{-1}a_j)^{\ell_2}(-1)^{m-k_2-\ell_2}\bigg)\\ &\quad = \binom{m+\frac{q-1}{d}}{k_1} \binom{m}{k_2} \sum_{\ell_1=0}^{m-k_1} \sum_{\ell_2=0}^{m-k_2} \binom{m-k_1}{\ell_1} \binom{m-k_2}{\ell_2} a_j^{\ell_1+\ell_2} \lambda^{m-k_1-\ell_1} (-1)^{m-k_2-\ell_2} \\ &\qquad \times \bigg(\sum_{i=1}^n c_i a_i^{(k_1+\ell_1)-(k_2+\ell_2)} \bigg). \end{align*} $$
Note that in the exponent of the last summand, we always have
![]() $0 \leq k_1+\ell _1 \leq m$
and
$0 \leq k_1+\ell _1 \leq m$
and
![]() $0 \leq k_2+\ell _2 \leq m$
so that
$0 \leq k_2+\ell _2 \leq m$
so that
![]() $-m \leq (k_1+\ell _1)-(k_2+\ell _2) \leq m$
, and thus
$-m \leq (k_1+\ell _1)-(k_2+\ell _2) \leq m$
, and thus
 $$ \begin{align*}\sum_{i=1}^n c_i a_i^{(k_1+\ell_1)-(k_2+\ell_2)}=0 \end{align*} $$
$$ \begin{align*}\sum_{i=1}^n c_i a_i^{(k_1+\ell_1)-(k_2+\ell_2)}=0 \end{align*} $$
by the assumptions in system (4.3). This proves the claim.
Then, for each
![]() $1\leq j \leq n$
and
$1\leq j \leq n$
and
![]() $0 \leq r \leq m-1$
, we apply Lemma 2.2 and equation (4.5) in the above claim to obtain that
$0 \leq r \leq m-1$
, we apply Lemma 2.2 and equation (4.5) in the above claim to obtain that
 $$ \begin{align*} E^{(r)} f (a_j) = \sum_{i=1}^n c_i \bigg(\sum_{k=0}^r E^{(k)}[(a_ix+\lambda)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(r-k)}[(a_i^{-1}x-1)^m](a_j)\bigg)=0. \end{align*} $$
$$ \begin{align*} E^{(r)} f (a_j) = \sum_{i=1}^n c_i \bigg(\sum_{k=0}^r E^{(k)}[(a_ix+\lambda)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(r-k)}[(a_i^{-1}x-1)^m](a_j)\bigg)=0. \end{align*} $$
Similarly, using Lemma 2.2, Lemma 2.3, system (4.3), and equation (4.5), we can compute
 $$ \begin{align*} E^{(m)} f (a_1) &= \sum_{i=1}^n c_i \bigg(\sum_{k=0}^m E^{(k)}[(a_ix+\lambda)^{m+\frac{q-1}{d}}](a_1) \cdot E^{(m-k)}[(a_i^{-1}x-1)^m](a_1)\bigg)\\ &= \sum_{i=1}^n c_i \bigg(E^{(0)}[(a_ix+\lambda)^{m+\frac{q-1}{d}}](a_1) \cdot E^{(m)}[(a_i^{-1}x-1)^m](a_1)\bigg) \\ & \quad + \sum_{i=1}^n c_i \bigg(E^{(m)}[(a_ix+\lambda)^{m+\frac{q-1}{d}}](a_1) \cdot E^{(0)}[(a_i^{-1}x-1)^m](a_1)\bigg)\\ &=\sum_{i=1}^n c_i (a_1a_i+\lambda)^{m+\frac{q-1}{d}} a_i^{-m} \\ &\quad + \binom{m+\frac{q-1}{d}}{m} \bigg(\sum_{i=1}^n c_i a_i^m (a_1a_i+\lambda)^{\frac{q-1}{d}} (a_i^{-1}a_1-1)^{m}\bigg). \end{align*} $$
$$ \begin{align*} E^{(m)} f (a_1) &= \sum_{i=1}^n c_i \bigg(\sum_{k=0}^m E^{(k)}[(a_ix+\lambda)^{m+\frac{q-1}{d}}](a_1) \cdot E^{(m-k)}[(a_i^{-1}x-1)^m](a_1)\bigg)\\ &= \sum_{i=1}^n c_i \bigg(E^{(0)}[(a_ix+\lambda)^{m+\frac{q-1}{d}}](a_1) \cdot E^{(m)}[(a_i^{-1}x-1)^m](a_1)\bigg) \\ & \quad + \sum_{i=1}^n c_i \bigg(E^{(m)}[(a_ix+\lambda)^{m+\frac{q-1}{d}}](a_1) \cdot E^{(0)}[(a_i^{-1}x-1)^m](a_1)\bigg)\\ &=\sum_{i=1}^n c_i (a_1a_i+\lambda)^{m+\frac{q-1}{d}} a_i^{-m} \\ &\quad + \binom{m+\frac{q-1}{d}}{m} \bigg(\sum_{i=1}^n c_i a_i^m (a_1a_i+\lambda)^{\frac{q-1}{d}} (a_i^{-1}a_1-1)^{m}\bigg). \end{align*} $$
Since
![]() $a_1a_i+\lambda \neq 0$
for each
$a_1a_i+\lambda \neq 0$
for each
![]() $1 \leq i \leq n$
, we have
$1 \leq i \leq n$
, we have
![]() $(a_1a_i+\lambda )^{\frac {q-1}{d}}=1$
for
$(a_1a_i+\lambda )^{\frac {q-1}{d}}=1$
for
![]() $i>1$
, and thus
$i>1$
, and thus
for all i. Since
![]() $a_1^2+\lambda \notin S_d \cup \{0\}$
, we have
$a_1^2+\lambda \notin S_d \cup \{0\}$
, we have
 $$ \begin{align*}(a_1^2+\lambda)^m \bigg((a_1^2+\lambda)^{\frac{q-1}{d}}-1\bigg) \neq 0. \end{align*} $$
$$ \begin{align*}(a_1^2+\lambda)^m \bigg((a_1^2+\lambda)^{\frac{q-1}{d}}-1\bigg) \neq 0. \end{align*} $$
Putting these altogether into the computation of
![]() $E^{(m)} f (a_1)$
, we have
$E^{(m)} f (a_1)$
, we have
 $$ \begin{align*} E^{(m)} f (a_1) &=\sum_{i=1}^n c_i (a_1a_i+\lambda)^{m+\frac{q-1}{d}} a_i^{-m} +\binom{m+\frac{q-1}{d}}{m} \sum_{i=1}^n c_i a_i^m (a_i^{-1}a_1-1)^{m}\\ &=c_1 a_1^{-m} \bigg((a_1^2+\lambda)^{m+\frac{q-1}{d}}-(a_1^2+\lambda)^m\bigg)+\sum_{i=1}^n c_i (a_1a_i+\lambda)^{m} a_i^{-m} \\ &+ \binom{m+\frac{q-1}{d}}{m} \sum_{k=0}^m \binom{m}{k} a_1^{m-k}(-1)^k \bigg(\sum_{i=1}^n c_i a_i^k\bigg)\\ &=c_1 a_1^{-m} (a_1^2+\lambda)^m \bigg((a_1^2+\lambda)^{\frac{q-1}{d}}-1\bigg) + \sum_{k=0}^m \binom{m}{k} a_1^{k}\lambda^{m-k} \bigg(\sum_{i=1}^n c_i a_i^{k-m}\bigg) \\ &=c_1 a_1^{-m} (a_1^2+\lambda)^m \bigg((a_1^2+\lambda)^{\frac{q-1}{d}}-1\bigg) \neq 0, \end{align*} $$
$$ \begin{align*} E^{(m)} f (a_1) &=\sum_{i=1}^n c_i (a_1a_i+\lambda)^{m+\frac{q-1}{d}} a_i^{-m} +\binom{m+\frac{q-1}{d}}{m} \sum_{i=1}^n c_i a_i^m (a_i^{-1}a_1-1)^{m}\\ &=c_1 a_1^{-m} \bigg((a_1^2+\lambda)^{m+\frac{q-1}{d}}-(a_1^2+\lambda)^m\bigg)+\sum_{i=1}^n c_i (a_1a_i+\lambda)^{m} a_i^{-m} \\ &+ \binom{m+\frac{q-1}{d}}{m} \sum_{k=0}^m \binom{m}{k} a_1^{m-k}(-1)^k \bigg(\sum_{i=1}^n c_i a_i^k\bigg)\\ &=c_1 a_1^{-m} (a_1^2+\lambda)^m \bigg((a_1^2+\lambda)^{\frac{q-1}{d}}-1\bigg) + \sum_{k=0}^m \binom{m}{k} a_1^{k}\lambda^{m-k} \bigg(\sum_{i=1}^n c_i a_i^{k-m}\bigg) \\ &=c_1 a_1^{-m} (a_1^2+\lambda)^m \bigg((a_1^2+\lambda)^{\frac{q-1}{d}}-1\bigg) \neq 0, \end{align*} $$
where we used the fact
![]() $c_1 \neq 0$
. In particular, f is not identically zero.
$c_1 \neq 0$
. In particular, f is not identically zero.
In conclusion, f is a non-zero polynomial with degree at most
![]() $\frac {q-1}{d}+2m$
, and Lemma 2.4 implies that each of
$\frac {q-1}{d}+2m$
, and Lemma 2.4 implies that each of
![]() $a_1,a_2, \ldots a_n$
is a root of f with multiplicity at least m. Recall that
$a_1,a_2, \ldots a_n$
is a root of f with multiplicity at least m. Recall that
![]() $m=n/2-1$
. It follows that
$m=n/2-1$
. It follows that
that is, we have
![]() $(n-2)^2 \leq \frac {2(q-1)}{d}.$
Therefore,
$(n-2)^2 \leq \frac {2(q-1)}{d}.$
Therefore,
![]() $n \leq \sqrt {2(q-1)/d}+2$
. This finishes the proof.
$n \leq \sqrt {2(q-1)/d}+2$
. This finishes the proof.
4.3 Applications to generalized Diophantine tuples over finite fields
In this subsection, we illustrate how to apply Theorems 1.1 and 4.2 for obtaining improved upper bounds on the size of a generalized Diophantine tuple or a strong generalized Diophantine tuple over
![]() $\mathbb {F}_{q}$
, when
$\mathbb {F}_{q}$
, when
![]() $q=p$
is a prime and q is a square.
$q=p$
is a prime and q is a square.
Proof of Theorem 1.5
(1) Let
![]() $A \subset {\mathbb F}_p^*$
with property
$A \subset {\mathbb F}_p^*$
with property
![]() $SD_d(\lambda , {\mathbb F}_p)$
, that is,
$SD_d(\lambda , {\mathbb F}_p)$
, that is,
![]() $AA+\lambda \subset S_d \cup \{0\}$
. Theorem 1.1 implies that
$AA+\lambda \subset S_d \cup \{0\}$
. Theorem 1.1 implies that
It follows that
![]() $(|A|-1)^2 \leq |S_d|$
. If
$(|A|-1)^2 \leq |S_d|$
. If
![]() $\lambda \in S_d$
, we have a stronger upper bound:
$\lambda \in S_d$
, we have a stronger upper bound:
It follows that
![]() $(|A|-\frac {1}{2})^2 \leq |S_d|-\frac {3}{4}$
.
$(|A|-\frac {1}{2})^2 \leq |S_d|-\frac {3}{4}$
.
(2) Let
![]() $A \subset {\mathbb F}_p^*$
with property
$A \subset {\mathbb F}_p^*$
with property
![]() $D_d(\lambda , {\mathbb F}_p)$
, that is,
$D_d(\lambda , {\mathbb F}_p)$
, that is,
![]() $A \hat {\times } A+\lambda \subset S_d \cup \{0\}$
. If
$A \hat {\times } A+\lambda \subset S_d \cup \{0\}$
. If
![]() $AA+\lambda \subset S_d \cup \{0\}$
, then (1) implies that
$AA+\lambda \subset S_d \cup \{0\}$
, then (1) implies that
![]() $|A|\leq \sqrt {p/d}+1$
and we are done. If
$|A|\leq \sqrt {p/d}+1$
and we are done. If
![]() $AA+\lambda \not \subset S_d \cup \{0\}$
, then Theorem 4.2 implies the required upper bound.
$AA+\lambda \not \subset S_d \cup \{0\}$
, then Theorem 4.2 implies the required upper bound.
Remark 4.3 Theorem 1.1 can be used to deduce a weaker upper bound of the form
![]() $2\sqrt {p/d}+O(1)$
for Theorem 1.5 (2). Let
$2\sqrt {p/d}+O(1)$
for Theorem 1.5 (2). Let
![]() $A \subset {\mathbb F}_p^*$
such that
$A \subset {\mathbb F}_p^*$
such that
![]() $A\hat {\times } A+\lambda \subset S_d \cup \{0\}$
. We can write
$A\hat {\times } A+\lambda \subset S_d \cup \{0\}$
. We can write
![]() $A=B \sqcup C$
such that
$A=B \sqcup C$
such that
![]() $|B|$
and
$|B|$
and
![]() $|C|$
differ by at most
$|C|$
differ by at most
![]() $1$
. Note that since B and C are disjoint, we have
$1$
. Note that since B and C are disjoint, we have
![]() $BC+\lambda \subset A \hat {\times } A+\lambda \subset S_d \cup \{0\}$
and thus Theorem 1.1 implies that
$BC+\lambda \subset A \hat {\times } A+\lambda \subset S_d \cup \{0\}$
and thus Theorem 1.1 implies that
![]() $|B||C| \leq p/d+|B|+|C|$
, which further implies that
$|B||C| \leq p/d+|B|+|C|$
, which further implies that
![]() $|A| \leq 2\sqrt {p/d}+O(1)$
. Note that such a weaker upper bound is worse than the trivial upper bound from character sums (Proposition 1.4) when
$|A| \leq 2\sqrt {p/d}+O(1)$
. Note that such a weaker upper bound is worse than the trivial upper bound from character sums (Proposition 1.4) when
![]() $d=2,3$
, and this is one of our main motivations for establishing the bound
$d=2,3$
, and this is one of our main motivations for establishing the bound
![]() $\sqrt {2p/d}+O(1)$
in Theorem 1.5 (2).
$\sqrt {2p/d}+O(1)$
in Theorem 1.5 (2).
Next, we consider the case q is a square. First we establish a non-trivial upper bound on
![]() $MSD_d(\lambda , {\mathbb F}_q)$
and
$MSD_d(\lambda , {\mathbb F}_q)$
and
![]() $MD_d(\lambda ,{\mathbb F}_q)$
under some minor assumption. While these new bounds only improve the trivial upper bound from character sums (Proposition 1.4) slightly, we will see these new bounds are sometimes sharp in the proof of Theorem 1.6. To achieve our goal, we need the following special case of Kummer’s theorem [Reference Kummer25].
$MD_d(\lambda ,{\mathbb F}_q)$
under some minor assumption. While these new bounds only improve the trivial upper bound from character sums (Proposition 1.4) slightly, we will see these new bounds are sometimes sharp in the proof of Theorem 1.6. To achieve our goal, we need the following special case of Kummer’s theorem [Reference Kummer25].
Lemma 4.4 Let p be a prime and
![]() $m,n$
be positive integers. If there is no carry between the addition of m and n in base-p, then
$m,n$
be positive integers. If there is no carry between the addition of m and n in base-p, then
![]() $\binom {m+n}{n}$
is not divisible by p.
$\binom {m+n}{n}$
is not divisible by p.
Theorem 4.5 Let q be a prime power and a square, and let
![]() $\lambda \in {\mathbb F}_q^*$
.
$\lambda \in {\mathbb F}_q^*$
.
-
(1) Let
 $d \geq 2$
be a divisor of
$d \geq 2$
be a divisor of
 $(q-1)$
. Let r be the remainder of
$(q-1)$
. Let r be the remainder of
 $\frac {q-1}{d}$
divided by
$\frac {q-1}{d}$
divided by
 $p\sqrt {q}$
. If
$p\sqrt {q}$
. If
 $r\leq (p-1)\sqrt {q}$
, then
$r\leq (p-1)\sqrt {q}$
, then
 $MSD_d(\lambda , {\mathbb F}_q)\leq \sqrt {q}-1$
.
$MSD_d(\lambda , {\mathbb F}_q)\leq \sqrt {q}-1$
. -
(2) Let
 $q \geq 25$
and let
$q \geq 25$
and let
 $d \geq 3$
be a divisor of
$d \geq 3$
be a divisor of
 $(q-1)$
. Let r be the remainder of
$(q-1)$
. Let r be the remainder of
 $\frac {q-1}{d}$
divided by
$\frac {q-1}{d}$
divided by
 $p\sqrt {q}$
. If
$p\sqrt {q}$
. If
 $r\leq (p-1)\sqrt {q}$
, then
$r\leq (p-1)\sqrt {q}$
, then
 $MD_d(\lambda , {\mathbb F}_q)\leq \sqrt {q}-1$
.
$MD_d(\lambda , {\mathbb F}_q)\leq \sqrt {q}-1$
.
Proof (1) Since
![]() $r\leq (p-1)\sqrt {q}$
, there is no carry between the addition of
$r\leq (p-1)\sqrt {q}$
, there is no carry between the addition of
![]() $r-1$
and
$r-1$
and
![]() $\sqrt {q}$
in base-p. Thus, there is no carry between the addition of
$\sqrt {q}$
in base-p. Thus, there is no carry between the addition of
![]() $\frac {q-1}{d}-1$
and
$\frac {q-1}{d}-1$
and
![]() $\sqrt {q}$
in base-p. It follows from Lemma 4.4 that
$\sqrt {q}$
in base-p. It follows from Lemma 4.4 that
 $$ \begin{align*}\binom{\sqrt{q}-1+\frac{q-1}{d}}{\sqrt{q}}\not \equiv 0 \quad\pmod p. \end{align*} $$
$$ \begin{align*}\binom{\sqrt{q}-1+\frac{q-1}{d}}{\sqrt{q}}\not \equiv 0 \quad\pmod p. \end{align*} $$
Let
![]() $A \subset {\mathbb F}_q^*$
with property
$A \subset {\mathbb F}_q^*$
with property
![]() $SD_d(\lambda , {\mathbb F}_q)$
such that
$SD_d(\lambda , {\mathbb F}_q)$
such that
![]() $|A|=MSD_d(\lambda , {\mathbb F}_q)$
. Note that Proposition 1.4 implies that
$|A|=MSD_d(\lambda , {\mathbb F}_q)$
. Note that Proposition 1.4 implies that
![]() $|A|\leq \sqrt {q}$
. For the sake of contradiction, assume that
$|A|\leq \sqrt {q}$
. For the sake of contradiction, assume that
![]() $|A|=\sqrt {q}$
. Note that
$|A|=\sqrt {q}$
. Note that
![]() $AA+\lambda \subset S_d \cup \{0\}$
and
$AA+\lambda \subset S_d \cup \{0\}$
and
 $$ \begin{align*}\binom{|A|-1+\frac{q-1}{d}}{|A|}=\binom{\sqrt{q}-1+\frac{q-1}{d}}{\sqrt{q}}\not \equiv 0 \quad\pmod p, \end{align*} $$
$$ \begin{align*}\binom{|A|-1+\frac{q-1}{d}}{|A|}=\binom{\sqrt{q}-1+\frac{q-1}{d}}{\sqrt{q}}\not \equiv 0 \quad\pmod p, \end{align*} $$
it follows from Theorem 1.1 that
that is,
![]() $|A|\leq \sqrt {|S_d|}+1<\sqrt {q}$
, a contradiction. This completes the proof.
$|A|\leq \sqrt {|S_d|}+1<\sqrt {q}$
, a contradiction. This completes the proof.
(2) Let
![]() $A \subset {\mathbb F}_q^*$
with property
$A \subset {\mathbb F}_q^*$
with property
![]() $D_d(\lambda , {\mathbb F}_q)$
such that
$D_d(\lambda , {\mathbb F}_q)$
such that
![]() $|A|=MD_d(\lambda , {\mathbb F}_q)$
. Then
$|A|=MD_d(\lambda , {\mathbb F}_q)$
. Then
![]() $A\hat {\times } A+\lambda \subset S_d \cup \{0\}$
. If
$A\hat {\times } A+\lambda \subset S_d \cup \{0\}$
. If
![]() $AA+\lambda \subset S_d \cup \{0\}$
, we just apply (1). Next assume that
$AA+\lambda \subset S_d \cup \{0\}$
, we just apply (1). Next assume that
![]() $AA+\lambda \not \subset S_d \cup \{0\}$
, then Theorem 4.2 implies that
$AA+\lambda \not \subset S_d \cup \{0\}$
, then Theorem 4.2 implies that
 $$ \begin{align*}|A| \leq \sqrt{\frac{2(q-1)}{d}}+4 \leq \sqrt{\frac{2(q-1)}{3}}+4\leq \sqrt{q} -1, \end{align*} $$
$$ \begin{align*}|A| \leq \sqrt{\frac{2(q-1)}{d}}+4 \leq \sqrt{\frac{2(q-1)}{3}}+4\leq \sqrt{q} -1, \end{align*} $$
provided that
![]() $q \geq 738$
. When
$q \geq 738$
. When
![]() $25 \leq q \leq 737$
, we have used SageMath to verify the theorem.
$25 \leq q \leq 737$
, we have used SageMath to verify the theorem.
Now we are ready to prove Theorem 1.6, which determines the maximum size of an infinitely family of generalized Diophantine tuples and strong generalized Diophantine tuples over finite fields.
Proof of Theorem 1.6
In both cases, the upper bound
![]() $\sqrt {q}-1$
follows from Theorem 4.5. To show that
$\sqrt {q}-1$
follows from Theorem 4.5. To show that
![]() $\sqrt {q}-1$
is a lower bound, we observe that
$\sqrt {q}-1$
is a lower bound, we observe that
![]() $A=\alpha {\mathbb F}_{\sqrt {q}}^*$
has property
$A=\alpha {\mathbb F}_{\sqrt {q}}^*$
has property
![]() $SD_{d}(\lambda ,\mathbb {F}_q)$
(and therefore
$SD_{d}(\lambda ,\mathbb {F}_q)$
(and therefore
![]() $D_{d}(\lambda ,\mathbb {F}_q)$
). Indeed,
$D_{d}(\lambda ,\mathbb {F}_q)$
). Indeed,
![]() $AA+\lambda =\alpha ^2 {\mathbb F}_{\sqrt {q}}^*+\lambda \subset \alpha ^2 {\mathbb F}_{\sqrt {q}} \subset S_d \cup \{0\}$
since
$AA+\lambda =\alpha ^2 {\mathbb F}_{\sqrt {q}}^*+\lambda \subset \alpha ^2 {\mathbb F}_{\sqrt {q}} \subset S_d \cup \{0\}$
since
![]() $\alpha ^2 \in S_d$
and
$\alpha ^2 \in S_d$
and
![]() ${\mathbb F}_{\sqrt {q}}^* \subset S_d$
(from the assumption
${\mathbb F}_{\sqrt {q}}^* \subset S_d$
(from the assumption
![]() $d \mid (\sqrt {q}+1)$
).
$d \mid (\sqrt {q}+1)$
).
Remark 4.6 Our SageMath code indicates that the last statement of Theorem 1.6 does not hold when
![]() $d=2$
and
$d=2$
and
![]() $q=9,25,49$
, when
$q=9,25,49$
, when
![]() $d=3$
and
$d=3$
and
![]() $q=4,16$
, and when
$q=4,16$
, and when
![]() $d=4$
and
$d=4$
and
![]() $q=9$
. We conjecture the same statement holds for
$q=9$
. We conjecture the same statement holds for
![]() $d=2$
, provided that q is sufficiently large.
$d=2$
, provided that q is sufficiently large.
So far we have only considered special cases of applying Theorem 1.1. In general, to apply Theorem 1.1, the assumption on the binomial coefficient in the statement of Theorem 1.1 might be tricky to analyze. However, if the base-p representation of
![]() $\frac {q-1}{d}$
behaves “nicely” (for example, if the order of p modulo d is small, then the base-p representation is periodic with a small period), then it is still convenient to apply Theorem 1.1. As a further illustration, we prove the following theorem. Note that the new bound is of the same shape as that in Theorem 1.5 (2), so it can be viewed as a generalization of Theorem 1.5 (2) as changing a prime p to an arbitrary power of p, provided that
$\frac {q-1}{d}$
behaves “nicely” (for example, if the order of p modulo d is small, then the base-p representation is periodic with a small period), then it is still convenient to apply Theorem 1.1. As a further illustration, we prove the following theorem. Note that the new bound is of the same shape as that in Theorem 1.5 (2), so it can be viewed as a generalization of Theorem 1.5 (2) as changing a prime p to an arbitrary power of p, provided that
![]() $d \mid (p-1)$
.
$d \mid (p-1)$
.
Theorem 4.7 Let
![]() $d \geq 2$
, and let q be a power of p such that
$d \geq 2$
, and let q be a power of p such that
![]() $d \mid (p-1)$
. Then
$d \mid (p-1)$
. Then
![]() $MD_d(\lambda , {\mathbb F}_q) \leq \sqrt {2(q-1)/d}+4$
for any
$MD_d(\lambda , {\mathbb F}_q) \leq \sqrt {2(q-1)/d}+4$
for any
![]() $\lambda \in {\mathbb F}_q^*$
.
$\lambda \in {\mathbb F}_q^*$
.
Proof Let
![]() $B \subset {\mathbb F}_q^*$
with property
$B \subset {\mathbb F}_q^*$
with property
![]() $D_d(\lambda , {\mathbb F}_q)$
, that is,
$D_d(\lambda , {\mathbb F}_q)$
, that is,
![]() $B\hat { \times } B+\lambda \subset S_d \cup \{0\}$
. If
$B\hat { \times } B+\lambda \subset S_d \cup \{0\}$
. If
![]() $BB+\lambda \nsubseteq S_d \cup \{0\}$
, we are done by Theorem 4.2. Thus, we may assume that
$BB+\lambda \nsubseteq S_d \cup \{0\}$
, we are done by Theorem 4.2. Thus, we may assume that
![]() $BB+\lambda \subset S_d \cup \{0\}$
. It suffices to show
$BB+\lambda \subset S_d \cup \{0\}$
. It suffices to show
![]() $|B| \leq \sqrt {2(q-1)/d}+4$
. To achieve that, we try to find an arbitrary subset A of B such that
$|B| \leq \sqrt {2(q-1)/d}+4$
. To achieve that, we try to find an arbitrary subset A of B such that
![]() $\binom {|A|-1+\frac {q-1}{d}}{|A|} \not \equiv 0\ \pmod p$
and
$\binom {|A|-1+\frac {q-1}{d}}{|A|} \not \equiv 0\ \pmod p$
and
![]() $|A|$
is as large as possible. With such a subset A, we have
$|A|$
is as large as possible. With such a subset A, we have
![]() $AB+\lambda \subset S_d \cup \{0\}$
so that we can apply Theorem 1.1. In the rest of the proof, we aim to find such an A with
$AB+\lambda \subset S_d \cup \{0\}$
so that we can apply Theorem 1.1. In the rest of the proof, we aim to find such an A with
![]() $|A|\geq |B|/2$
so that, from Theorem 1.1, we can deduce
$|A|\geq |B|/2$
so that, from Theorem 1.1, we can deduce
 $$ \begin{align*}\frac{|B|^2}{2} \leq \frac{q-1}{d}+2|B|-1 \implies |B| \leq \sqrt{\frac{2(q-1)}{d}+2}+2<\sqrt{\frac{2(q-1)}{d}}+4. \end{align*} $$
$$ \begin{align*}\frac{|B|^2}{2} \leq \frac{q-1}{d}+2|B|-1 \implies |B| \leq \sqrt{\frac{2(q-1)}{d}+2}+2<\sqrt{\frac{2(q-1)}{d}}+4. \end{align*} $$
Write
![]() $|B|-1=(c_k, c_{k-1}, \ldots , c_1,c_0)_p$
in base-p, that is,
$|B|-1=(c_k, c_{k-1}, \ldots , c_1,c_0)_p$
in base-p, that is,
![]() $|B|-1=\sum _{i=0}^k c_ip^i$
with
$|B|-1=\sum _{i=0}^k c_ip^i$
with
![]() $0 \leq c_i \leq p-1$
for each
$0 \leq c_i \leq p-1$
for each
![]() $0 \leq i \leq k$
and
$0 \leq i \leq k$
and
![]() $c_k \geq 1$
. Next, we construct A according to the size of
$c_k \geq 1$
. Next, we construct A according to the size of
![]() $c_k$
.
$c_k$
.
Case 1.
![]() $c_k \leq p-1-\frac {p-1}{d}$
. In this case, let A be an arbitrary subset of B with
$c_k \leq p-1-\frac {p-1}{d}$
. In this case, let A be an arbitrary subset of B with
![]() $|A|-1=(c_k,0, \ldots , 0)_p$
, that is,
$|A|-1=(c_k,0, \ldots , 0)_p$
, that is,
![]() $|A|=c_kp^k+1$
. It is easy to verify that
$|A|=c_kp^k+1$
. It is easy to verify that
![]() $\binom {|A|-1+\frac {q-1}{d}}{|A|} \not \equiv 0 \ \pmod p$
using Lemma 4.4. Since
$\binom {|A|-1+\frac {q-1}{d}}{|A|} \not \equiv 0 \ \pmod p$
using Lemma 4.4. Since
![]() $|B| \leq (c_k+1)p^k$
, it also follows readily that
$|B| \leq (c_k+1)p^k$
, it also follows readily that
![]() $|A|\geq |B|/2$
.
$|A|\geq |B|/2$
.
Case 2.
![]() $c_k> p-1-\frac {p-1}{d}$
. In this case, let A be an arbitrary subset of B with
$c_k> p-1-\frac {p-1}{d}$
. In this case, let A be an arbitrary subset of B with
 $$ \begin{align*}|A|-1=\bigg(\frac{(d-1)(p-1)}{d},\frac{(d-1)(p-1)}{d}, \ldots, \frac{(d-1)(p-1)}{d}\bigg)_p,\end{align*} $$
$$ \begin{align*}|A|-1=\bigg(\frac{(d-1)(p-1)}{d},\frac{(d-1)(p-1)}{d}, \ldots, \frac{(d-1)(p-1)}{d}\bigg)_p,\end{align*} $$
that is,
![]() $|A|=\frac {(d-1)(p-1)}{d} \cdot \sum _{i=0}^k p^i +1$
. Again, it is easy to verify that
$|A|=\frac {(d-1)(p-1)}{d} \cdot \sum _{i=0}^k p^i +1$
. Again, it is easy to verify that
![]() $\binom {|A|-1+\frac {q-1}{d}}{|A|} \not \equiv 0 \ \pmod p$
using Lemma 4.4. Since
$\binom {|A|-1+\frac {q-1}{d}}{|A|} \not \equiv 0 \ \pmod p$
using Lemma 4.4. Since
![]() $d \geq 2$
, it follows that
$d \geq 2$
, it follows that
![]() $2|A| \geq (p-1)\sum _{i=0}^k p^i +2= p^{k+1}+1>|B|$
.
$2|A| \geq (p-1)\sum _{i=0}^k p^i +2= p^{k+1}+1>|B|$
.
Remark 4.8 Under the same assumption, the proof of Theorem 4.7 can be refined to obtain improved upper bounds on
![]() $MSD_d(\lambda , {\mathbb F}_q)$
. In particular, if
$MSD_d(\lambda , {\mathbb F}_q)$
. In particular, if
![]() $d,r \geq 2$
are fixed, and
$d,r \geq 2$
are fixed, and
![]() $p \equiv 1 \ \pmod d$
is a prime, then as
$p \equiv 1 \ \pmod d$
is a prime, then as
![]() $p \to \infty $
, we can show that
$p \to \infty $
, we can show that
![]() $MSD_d(\lambda , {\mathbb F}_{p^{2r-1}}) \leq (1+o(1))\sqrt {p^{2r-1}/d}$
uniformly among
$MSD_d(\lambda , {\mathbb F}_{p^{2r-1}}) \leq (1+o(1))\sqrt {p^{2r-1}/d}$
uniformly among
![]() $\lambda \in {\mathbb F}_{p^{2r-1}}^{*}$
. Indeed, if
$\lambda \in {\mathbb F}_{p^{2r-1}}^{*}$
. Indeed, if
![]() $B \subset {\mathbb F}_q^*$
with property
$B \subset {\mathbb F}_q^*$
with property
![]() $D_d(\lambda , {\mathbb F}_q)$
with
$D_d(\lambda , {\mathbb F}_q)$
with
![]() $q=p^{2r-1}$
and
$q=p^{2r-1}$
and
![]() $\lambda \in {\mathbb F}_{q}^{*}$
, then we can assume without loss of generality that
$\lambda \in {\mathbb F}_{q}^{*}$
, then we can assume without loss of generality that
![]() $\sqrt {q/d}<|B|$
. Otherwise, we are done. Note that
$\sqrt {q/d}<|B|$
. Otherwise, we are done. Note that
![]() $|B|<\sqrt {q}+O(1)$
by Proposition 1.4. Following the notations used in the proof of Theorem 4.7, we have
$|B|<\sqrt {q}+O(1)$
by Proposition 1.4. Following the notations used in the proof of Theorem 4.7, we have
![]() $\sqrt {p/d}-1\leq c_k \leq \sqrt {p}$
and thus we are always in Case 1, and the same construction of A gives
$\sqrt {p/d}-1\leq c_k \leq \sqrt {p}$
and thus we are always in Case 1, and the same construction of A gives
![]() $|A|=(1-o(1))|B|$
as
$|A|=(1-o(1))|B|$
as
![]() $p \to \infty $
. Thus, Theorem 1.1 gives
$p \to \infty $
. Thus, Theorem 1.1 gives
![]() $|B| \leq (1+o(1))\sqrt {q/d}$
.
$|B| \leq (1+o(1))\sqrt {q/d}$
.
5 Improved upper bounds on the largest size of generalized Diophantine tuples over integers
5.1 Proof of Theorem 1.2
In this subsection, we improve the upper bounds on the largest size of generalized Diophantine tuples with property
![]() $D_{k}(n)$
. We first recall that for each
$D_{k}(n)$
. We first recall that for each
![]() $n \ge 1$
and
$n \ge 1$
and
![]() $k \ge 2$
,
$k \ge 2$
,
For
![]() $k \geq 2$
, we defined the constant in the introduction
$k \geq 2$
, we defined the constant in the introduction
 $$ \begin{align} \eta_k=\min_{\mathcal{I}} \frac{|\mathcal{I}|}{T_{\mathcal{I}}^2}, \end{align} $$
$$ \begin{align} \eta_k=\min_{\mathcal{I}} \frac{|\mathcal{I}|}{T_{\mathcal{I}}^2}, \end{align} $$
where the minimum is taken over all nonempty subset
![]() $\mathcal {I}$
of
$\mathcal {I}$
of
and
Here is the proof of our main theorem, Theorem 1.2.
Proof of Theorem 1.2
Let
![]() $A=\{a_{1},a_{2},\ldots ,a_{m}\}$
be a generalized Diophantine m-tuple with property
$A=\{a_{1},a_{2},\ldots ,a_{m}\}$
be a generalized Diophantine m-tuple with property
![]() $D_{k}(n)$
and
$D_{k}(n)$
and
![]() $k\geq 3$
. Given the assumption that
$k\geq 3$
. Given the assumption that
![]() $\log k=O(\sqrt {\log \log n})$
, Proposition 2.9 implies that the contribution of
$\log k=O(\sqrt {\log \log n})$
, Proposition 2.9 implies that the contribution of
![]() $a_i$
with
$a_i$
with
![]() $a_i>n^{\frac {k}{k-2}}$
is
$a_i>n^{\frac {k}{k-2}}$
is
![]() $|A\cap (n^{\frac {k}{k-2}},\infty )|=O(\log k \log \log k)$
is negligible. Thus, we can assume that
$|A\cap (n^{\frac {k}{k-2}},\infty )|=O(\log k \log \log k)$
is negligible. Thus, we can assume that
![]() $A \subset [1, n^{\frac {k}{k-2}}]$
. Let
$A \subset [1, n^{\frac {k}{k-2}}]$
. Let
![]() $\mathcal {I}$
be a nonempty subset of
$\mathcal {I}$
be a nonempty subset of
![]() $\{1 \leq i \leq k: \gcd (i,k)=1, \gcd (i-1,k)>1\}$
, such that the ratio
$\{1 \leq i \leq k: \gcd (i,k)=1, \gcd (i-1,k)>1\}$
, such that the ratio
![]() $|\mathcal {I}|/T_{\mathcal {I}}^2$
in equation (5.1) is minimized by
$|\mathcal {I}|/T_{\mathcal {I}}^2$
in equation (5.1) is minimized by
![]() $\mathcal {I}$
. In other words, we have
$\mathcal {I}$
. In other words, we have
![]() $\eta _k=|\mathcal {I}|/T_{\mathcal {I}}^2$
, where
$\eta _k=|\mathcal {I}|/T_{\mathcal {I}}^2$
, where
To apply the Gallagher sieve inequality (Theorem 2.5), we set
![]() $N=n^{\frac {k}{k-2}}$
and define the set of primes
$N=n^{\frac {k}{k-2}}$
and define the set of primes
For each prime
![]() $p \in \mathcal {P}$
, denote by
$p \in \mathcal {P}$
, denote by
![]() $A_{p}$
the image of
$A_{p}$
the image of
![]() $A \ \pmod {p}$
and let
$A \ \pmod {p}$
and let
![]() $A_p^*=A_p \setminus \{0\}$
.
$A_p^*=A_p \setminus \{0\}$
.
Let
![]() $p \in \mathcal {P}$
. We can naturally view
$p \in \mathcal {P}$
. We can naturally view
![]() $A_p^*$
as a subset of
$A_p^*$
as a subset of
![]() ${\mathbb F}_p^*$
. Since A has property
${\mathbb F}_p^*$
. Since A has property
![]() $D_k(n)$
, it follows that
$D_k(n)$
, it follows that
![]() $A_p^* \hat { \times } A_p^*+ n \subset \{x^k: x \in {\mathbb F}_p^*\} \cup \{0\}$
. Note that
$A_p^* \hat { \times } A_p^*+ n \subset \{x^k: x \in {\mathbb F}_p^*\} \cup \{0\}$
. Note that
![]() $\{x^k: x \in {\mathbb F}_p^*\}$
is the multiplicative subgroup of
$\{x^k: x \in {\mathbb F}_p^*\}$
is the multiplicative subgroup of
![]() ${\mathbb F}_p^*$
with order
${\mathbb F}_p^*$
with order
![]() $\frac {p-1}{\gcd (p-1,k)}$
. Since
$\frac {p-1}{\gcd (p-1,k)}$
. Since
![]() $\gcd (p-1,k)>1$
and
$\gcd (p-1,k)>1$
and
![]() $p \nmid n$
, Theorem 1.5 (2) implies that
$p \nmid n$
, Theorem 1.5 (2) implies that
 $$\begin{align*}|A_{p}| \leq |A_p^*|+1 \leq \sqrt{\frac{2(p-1)}{\gcd(p-1,k)}}+5.\end{align*}$$
$$\begin{align*}|A_{p}| \leq |A_p^*|+1 \leq \sqrt{\frac{2(p-1)}{\gcd(p-1,k)}}+5.\end{align*}$$
Set
![]() $Q=2(\frac {\phi (k)\log N}{T})^2$
. Applying Gallagher’s larger sieve, we obtain that
$Q=2(\frac {\phi (k)\log N}{T})^2$
. Applying Gallagher’s larger sieve, we obtain that
 $$ \begin{align} |A| \le \frac{\sum_{p \in \mathcal{P},p \le Q}\log p - \log N}{\sum_{p \in \mathcal{P},p \le Q} \frac{\log p}{|A_{p}|}-\log N}. \end{align} $$
$$ \begin{align} |A| \le \frac{\sum_{p \in \mathcal{P},p \le Q}\log p - \log N}{\sum_{p \in \mathcal{P},p \le Q} \frac{\log p}{|A_{p}|}-\log N}. \end{align} $$
Let c be the constant from Corollary 2.7. For the numerator on the right-hand side of inequality (5.3), we have
 $$ \begin{align*} \sum_{p \in \mathcal{P},p \le Q}\log p - \log N & \leq \sum_{i \in \mathcal{I}}\bigg(\sum_{\substack{p\equiv i \text{ mod }k, \\p \le Q}}\log p\bigg) - \log N \\ &=\frac{|\mathcal{I}|Q}{\phi(k)}+O\bigg(|\mathcal{I}|Q\exp(-c\sqrt{\log Q})\bigg)-\log N. \end{align*} $$
$$ \begin{align*} \sum_{p \in \mathcal{P},p \le Q}\log p - \log N & \leq \sum_{i \in \mathcal{I}}\bigg(\sum_{\substack{p\equiv i \text{ mod }k, \\p \le Q}}\log p\bigg) - \log N \\ &=\frac{|\mathcal{I}|Q}{\phi(k)}+O\bigg(|\mathcal{I}|Q\exp(-c\sqrt{\log Q})\bigg)-\log N. \end{align*} $$
Next, we estimate the denominator on the right-hand side of inequality (5.3). Note that
![]() $|\mathcal {I}|\le T=\sum _{i \in \mathcal {I}} \sqrt {\gcd (i-1,k)}$
. Then we have
$|\mathcal {I}|\le T=\sum _{i \in \mathcal {I}} \sqrt {\gcd (i-1,k)}$
. Then we have
![]() $T \le |\mathcal {I}| \sqrt {k} \le \phi (k)\sqrt {k}$
, and so
$T \le |\mathcal {I}| \sqrt {k} \le \phi (k)\sqrt {k}$
, and so
![]() $\phi (k)/T \ge 1/\sqrt {k}$
. Since
$\phi (k)/T \ge 1/\sqrt {k}$
. Since
![]() $k=(\log N)^{o(1)}$
, we deduce
$k=(\log N)^{o(1)}$
, we deduce
![]() $Q> 2(\log N)^{2-o(1)}$
. Thus we have
$Q> 2(\log N)^{2-o(1)}$
. Thus we have
![]() $k=Q^{o(1)}$
. This, together with Corollary 2.7 and Lemma 2.8, deduces that for each
$k=Q^{o(1)}$
. This, together with Corollary 2.7 and Lemma 2.8, deduces that for each
![]() $i \in \mathcal {I}$
,
$i \in \mathcal {I}$
,
 $$ \begin{align*} \sum_{\substack{p \in \mathcal{P}, p \le Q\\ p \equiv i \text{ mod } k}} \frac{\log p}{|A_{p}|} & \geq \sum_{\substack{p \in \mathcal{P}, p \le Q \\ p \equiv i \text{ mod } k}} \frac{\log p}{\sqrt{\frac{2(p-1)}{\gcd(i-1,k)}}+5}\\ &=\sum_{\substack{p \le Q\\ p \equiv i \text{ mod } k}} \frac{\log p}{\sqrt{\frac{2p}{\gcd(i-1,k)}}}+O\bigg(\sum_{p \le Q} \frac{k\log p}{p}\bigg)+O\bigg(\sum_{p \mid n} \frac{\sqrt{k}\log p}{\sqrt{p}}\bigg)\\ &=\sqrt{\frac{\gcd(i-1,k)}{2}} \sum_{\substack{p \le Q\\ p \equiv i \text{ mod } k}} \frac{\log p}{\sqrt{p}}+O(k\log Q)+O(k (\log n)^{1/2})\\ &=\frac{\sqrt{2Q\gcd(i-1,k)}}{\phi(k)} +O\left( \sqrt{Q} \sqrt{\gcd(i-1,k)} \exp(-c\sqrt{\log Q}) \right). \end{align*} $$
$$ \begin{align*} \sum_{\substack{p \in \mathcal{P}, p \le Q\\ p \equiv i \text{ mod } k}} \frac{\log p}{|A_{p}|} & \geq \sum_{\substack{p \in \mathcal{P}, p \le Q \\ p \equiv i \text{ mod } k}} \frac{\log p}{\sqrt{\frac{2(p-1)}{\gcd(i-1,k)}}+5}\\ &=\sum_{\substack{p \le Q\\ p \equiv i \text{ mod } k}} \frac{\log p}{\sqrt{\frac{2p}{\gcd(i-1,k)}}}+O\bigg(\sum_{p \le Q} \frac{k\log p}{p}\bigg)+O\bigg(\sum_{p \mid n} \frac{\sqrt{k}\log p}{\sqrt{p}}\bigg)\\ &=\sqrt{\frac{\gcd(i-1,k)}{2}} \sum_{\substack{p \le Q\\ p \equiv i \text{ mod } k}} \frac{\log p}{\sqrt{p}}+O(k\log Q)+O(k (\log n)^{1/2})\\ &=\frac{\sqrt{2Q\gcd(i-1,k)}}{\phi(k)} +O\left( \sqrt{Q} \sqrt{\gcd(i-1,k)} \exp(-c\sqrt{\log Q}) \right). \end{align*} $$
Thus we have
 $$ \begin{align*} |A| &\le \frac{\sum_{p \in \mathcal{P},p \le Q}\log p - \log N}{\sum_{p \in \mathcal{P},p \le Q} \frac{\log p}{|A_{p}|}-\log N}\\ &\le \frac{\frac{|\mathcal{I}|Q}{\phi(k)}+O(|\mathcal{I}|Q\exp(-c\sqrt{\log Q}))-\log N}{\sum_{i \in \mathcal{I}}\bigg( \sum_{\substack{p \in \mathcal{P}, p \le Q\\ p \equiv i \text{ mod } k}} \frac{\log p}{|A_{p}|}\bigg) -\log N}\\ &\le \frac{\frac{|\mathcal{I}|Q}{\phi(k)}+O(|\mathcal{I}|Q\exp(-c\sqrt{\log Q}))-\log N}{\frac{T\sqrt{2Q}}{\phi(k)}+O\left(T \sqrt{Q} \exp(-c\sqrt{\log Q}) \right)-\log N}. \end{align*} $$
$$ \begin{align*} |A| &\le \frac{\sum_{p \in \mathcal{P},p \le Q}\log p - \log N}{\sum_{p \in \mathcal{P},p \le Q} \frac{\log p}{|A_{p}|}-\log N}\\ &\le \frac{\frac{|\mathcal{I}|Q}{\phi(k)}+O(|\mathcal{I}|Q\exp(-c\sqrt{\log Q}))-\log N}{\sum_{i \in \mathcal{I}}\bigg( \sum_{\substack{p \in \mathcal{P}, p \le Q\\ p \equiv i \text{ mod } k}} \frac{\log p}{|A_{p}|}\bigg) -\log N}\\ &\le \frac{\frac{|\mathcal{I}|Q}{\phi(k)}+O(|\mathcal{I}|Q\exp(-c\sqrt{\log Q}))-\log N}{\frac{T\sqrt{2Q}}{\phi(k)}+O\left(T \sqrt{Q} \exp(-c\sqrt{\log Q}) \right)-\log N}. \end{align*} $$
Finally, recall that
![]() $Q=2(\frac {\phi (k)\log N}{T})^2$
. It follows that
$Q=2(\frac {\phi (k)\log N}{T})^2$
. It follows that
 $$ \begin{align*} |A|&\leq \frac{2|\mathcal{I}|\phi(k)(\frac{\log N}{T})^2+O\left(|\mathcal{I}| (\frac{\phi(k)\log N}{T})^2\exp \Big(-c\sqrt{\log (\frac{\phi(k)\log N}{T})}\Big)\right)}{2\log N+O\left(\phi(k)\log N\exp \Big(-c\sqrt{\log (\frac{\phi(k)\log N}{T})}\Big)\right)-\log N}\\ &= \frac{\frac{2|\mathcal{I}|\phi(k)}{T^2} \log N+O\left(\frac{|\mathcal{I}|\phi(k)^2 \log N}{T^2} \exp \Big(-c\sqrt{\log (\frac{\phi(k)\log N}{T})}\Big)\right)}{1+O\left(\phi(k) \exp \Big(-c\sqrt{\log (\frac{\phi(k)\log N}{T})}\Big)\right)}. \end{align*} $$
$$ \begin{align*} |A|&\leq \frac{2|\mathcal{I}|\phi(k)(\frac{\log N}{T})^2+O\left(|\mathcal{I}| (\frac{\phi(k)\log N}{T})^2\exp \Big(-c\sqrt{\log (\frac{\phi(k)\log N}{T})}\Big)\right)}{2\log N+O\left(\phi(k)\log N\exp \Big(-c\sqrt{\log (\frac{\phi(k)\log N}{T})}\Big)\right)-\log N}\\ &= \frac{\frac{2|\mathcal{I}|\phi(k)}{T^2} \log N+O\left(\frac{|\mathcal{I}|\phi(k)^2 \log N}{T^2} \exp \Big(-c\sqrt{\log (\frac{\phi(k)\log N}{T})}\Big)\right)}{1+O\left(\phi(k) \exp \Big(-c\sqrt{\log (\frac{\phi(k)\log N}{T})}\Big)\right)}. \end{align*} $$
Recall that
![]() $N=n^{\frac {k}{k-2}}$
. Thus, to obtain our desired result, we need to show
$N=n^{\frac {k}{k-2}}$
. Thus, to obtain our desired result, we need to show
 $$ \begin{align*} |A|\leq \frac{(1+o(1))\frac{2|\mathcal{I}|\phi(k)}{T^2} \log N}{1-o(1)}, \end{align*} $$
$$ \begin{align*} |A|\leq \frac{(1+o(1))\frac{2|\mathcal{I}|\phi(k)}{T^2} \log N}{1-o(1)}, \end{align*} $$
and it suffices to show that
 $$\begin{align*}\phi(k)\exp \Big(-c\sqrt{\log (\frac{\phi(k)\log N}{T})}\Big)=o(1),\end{align*}$$
$$\begin{align*}\phi(k)\exp \Big(-c\sqrt{\log (\frac{\phi(k)\log N}{T})}\Big)=o(1),\end{align*}$$
as
![]() $N \to \infty $
, or equivalently,
$N \to \infty $
, or equivalently,
 $$\begin{align*}\log k- c\sqrt{\log \frac{\phi(k)}{T}+\log \log N} \to -\infty,\end{align*}$$
$$\begin{align*}\log k- c\sqrt{\log \frac{\phi(k)}{T}+\log \log N} \to -\infty,\end{align*}$$
as
![]() $N \to \infty $
. We notice that
$N \to \infty $
. We notice that
![]() $\phi (k)/T \ge 1/\sqrt {k}$
. Let
$\phi (k)/T \ge 1/\sqrt {k}$
. Let
![]() $c'=c/2$
. Then the assumption
$c'=c/2$
. Then the assumption
![]() $\log k\leq c'\sqrt {\log \log n}<c'\sqrt {\log \log N}$
implies
$\log k\leq c'\sqrt {\log \log n}<c'\sqrt {\log \log N}$
implies
and
 $$\begin{align*}\log k - c\sqrt{\log \frac{\phi(k)}{T}+\log \log N} \leq -(c'-o(1))\log \log N \to -\infty,\end{align*}$$
$$\begin{align*}\log k - c\sqrt{\log \frac{\phi(k)}{T}+\log \log N} \leq -(c'-o(1))\log \log N \to -\infty,\end{align*}$$
as required.
Remark 5.1 Note that when
![]() $\mathcal {I}=\{1\}$
, that is to say, when we only consider primes p such that
$\mathcal {I}=\{1\}$
, that is to say, when we only consider primes p such that
![]() $p \equiv 1 \ \pmod k$
for applying the Gallagher inequality, the condition
$p \equiv 1 \ \pmod k$
for applying the Gallagher inequality, the condition
![]() $p \equiv 1 \ \pmod k$
guarantees that the kth powers are indeed kth powers modulo p. We have
$p \equiv 1 \ \pmod k$
guarantees that the kth powers are indeed kth powers modulo p. We have
![]() $T=T_{\mathcal {I}}=\sqrt {k}$
, thus we trivially have
$T=T_{\mathcal {I}}=\sqrt {k}$
, thus we trivially have
![]() $\eta _k \leq \frac {1}{k}$
in view of equation (5.1). In particular, if k is fixed and
$\eta _k \leq \frac {1}{k}$
in view of equation (5.1). In particular, if k is fixed and
![]() $n \to \infty $
, Theorem 1.2 implies that
$n \to \infty $
, Theorem 1.2 implies that
which already provides a substantial improvement on the best-known upper bound
![]() $M_k(n)\leq (3\phi (k)+o(1))\log n$
whenever
$M_k(n)\leq (3\phi (k)+o(1))\log n$
whenever
![]() $k \geq 3$
given in [Reference Dixit, Kim and Murty7]. Moreover, note that
$k \geq 3$
given in [Reference Dixit, Kim and Murty7]. Moreover, note that
![]() $\frac {\phi (k)}{k}$
can be as small as
$\frac {\phi (k)}{k}$
can be as small as
![]() $O(\frac {1}{\log \log k})$
when k is the product of distinct primes [Reference Montgomery and Vaughan28, Theorem 2.9]. Thus, in view of Theorem 1.2, the inequality (5.4) already shows there is
$O(\frac {1}{\log \log k})$
when k is the product of distinct primes [Reference Montgomery and Vaughan28, Theorem 2.9]. Thus, in view of Theorem 1.2, the inequality (5.4) already shows there is
![]() $k=k(n)$
such that
$k=k(n)$
such that
![]() $\log k \asymp \sqrt {\log \log n}$
and
$\log k \asymp \sqrt {\log \log n}$
and
 $$ \begin{align} M_k(n)\ll \frac{\log n}{\log \log k} \ll \frac{\log n}{\log \log \log n}. \end{align} $$
$$ \begin{align} M_k(n)\ll \frac{\log n}{\log \log k} \ll \frac{\log n}{\log \log \log n}. \end{align} $$
Note that (5.5) already breaks the
![]() $\log n$
barrier. On the other hand, we can still use other primes p such that
$\log n$
barrier. On the other hand, we can still use other primes p such that
![]() $\gcd (p-1,k)>1$
for which kth powers are in fact
$\gcd (p-1,k)>1$
for which kth powers are in fact
![]() $\gcd (k,p-1)$
th powers modulo p when we apply the Gallagher sieve inequality. We can take advantage of the improvement on the upper bound of
$\gcd (k,p-1)$
th powers modulo p when we apply the Gallagher sieve inequality. We can take advantage of the improvement on the upper bound of
![]() $M_{k}(n)$
. In the next two subsections, we further provide a significant improvement on inequality (5.5).
$M_{k}(n)$
. In the next two subsections, we further provide a significant improvement on inequality (5.5).
Next, we define a strong Diophantine m-tuple with property
![]() $SD_{k}(n)$
to be a set
$SD_{k}(n)$
to be a set
![]() $\{a_1,\ldots , a_m\}$
of m distinct positive integers such that
$\{a_1,\ldots , a_m\}$
of m distinct positive integers such that
![]() $a_{i}a_{j}+n$
is a kth power for any choice of i and j. We have a stronger upper bound for the size of a strong Diophantine tuple with property
$a_{i}a_{j}+n$
is a kth power for any choice of i and j. We have a stronger upper bound for the size of a strong Diophantine tuple with property
![]() $SD_k(n)$
. We define
$SD_k(n)$
. We define
Theorem 5.2 There is a constant
![]() $c'>0$
, such that as
$c'>0$
, such that as
![]() $n \to \infty $
,
$n \to \infty $
,
 $$ \begin{align*}MS_k(n)\leq \bigg(\frac{k}{k-2}+o(1)\bigg) \ \eta_k \phi(k) \log n, \end{align*} $$
$$ \begin{align*}MS_k(n)\leq \bigg(\frac{k}{k-2}+o(1)\bigg) \ \eta_k \phi(k) \log n, \end{align*} $$
holds uniformly for positive integers
![]() $k,n \geq 3$
such that
$k,n \geq 3$
such that
![]() $\log k \leq c'\sqrt {\log \log n}$
. Moreover, if k is even, under the same assumption (including the case
$\log k \leq c'\sqrt {\log \log n}$
. Moreover, if k is even, under the same assumption (including the case
![]() $k=2$
), we have the stronger bound
$k=2$
), we have the stronger bound
where
![]() $\tau (n)$
is the number of divisors of n.
$\tau (n)$
is the number of divisors of n.
Proof The proof is very similar to the proof of Theorem 1.2 and we follow all the notations and steps as in the proof of Theorem 1.2, apart from the minor modifications stated below.
We prove the first part. For each
![]() $p \in \mathcal {P}$
, we have the stronger upper bound that
$p \in \mathcal {P}$
, we have the stronger upper bound that
![]() $|A_p| \leq \sqrt {\frac {(p-1)}{\gcd (p-1,k)}}+2$
by Theorem 1.5 (2). To optimize the upper bound obtained from Gallagher’s larger sieve, we instead set
$|A_p| \leq \sqrt {\frac {(p-1)}{\gcd (p-1,k)}}+2$
by Theorem 1.5 (2). To optimize the upper bound obtained from Gallagher’s larger sieve, we instead set
![]() $Q=(\frac {\phi (k)\log N}{T})^2$
.
$Q=(\frac {\phi (k)\log N}{T})^2$
.
Next, we assume that k is even and prove the second part. Notice that for each
![]() $x \in A$
, there is a positive integer y, such that
$x \in A$
, there is a positive integer y, such that
![]() $x^2+n=y^2$
. Thus,
$x^2+n=y^2$
. Thus,
![]() $|A|$
is bounded by the number of positive integral solutions to the equation
$|A|$
is bounded by the number of positive integral solutions to the equation
![]() $x^2+n=y^2$
, which is at most
$x^2+n=y^2$
, which is at most
![]() $\tau (n)$
. On the other hand, this also implies that all the elements in A are at most n. Thus, we can set
$\tau (n)$
. On the other hand, this also implies that all the elements in A are at most n. Thus, we can set
![]() $N=n$
instead and obtain the stronger upper bound.
$N=n$
instead and obtain the stronger upper bound.
5.2 Proof of Theorem 1.3
In this subsection, by finding a more refined upper bound on
![]() $\eta _k$
in equation (5.1), we show that the same approach significantly improves the upper bound of
$\eta _k$
in equation (5.1), we show that the same approach significantly improves the upper bound of
![]() $M_{k}(n)$
in inequality (5.5) when k is the product of the first few distinct primes.
$M_{k}(n)$
in inequality (5.5) when k is the product of the first few distinct primes.
We label all the primes in increasing order so that
![]() $2=p_1<p_2<\cdots <p_{\ell }<\cdots $
. Let
$2=p_1<p_2<\cdots <p_{\ell }<\cdots $
. Let
![]() $P_{\ell }=\prod _{i=1}^{\ell } p_i$
be the product of first
$P_{\ell }=\prod _{i=1}^{\ell } p_i$
be the product of first
![]() $\ell $
primes. Let
$\ell $
primes. Let
![]() $\mathcal {I}_1=\{1\}$
. For
$\mathcal {I}_1=\{1\}$
. For
![]() $\ell \geq 1$
, we define
$\ell \geq 1$
, we define
![]() $\mathcal {I}_{\ell +1}$
inductively:
$\mathcal {I}_{\ell +1}$
inductively:
We note that
![]() $\mathcal {I}_{\ell }\subset \mathcal {I}_{\ell +1}$
for any
$\mathcal {I}_{\ell }\subset \mathcal {I}_{\ell +1}$
for any
![]() $\ell \geq 1$
. Also, it is clear that
$\ell \geq 1$
. Also, it is clear that
Lemma 5.3 Following the above definitions, we have
Proof We give an inductive proof. When
![]() $\ell =1$
, the inclusion (5.8) holds. We assume that (5.8) holds for some
$\ell =1$
, the inclusion (5.8) holds. We assume that (5.8) holds for some
![]() $\ell \geq 1$
. Let
$\ell \geq 1$
. Let
![]() $x=i+jP_{\ell } \in \mathcal {I}_{\ell +1}$
. By the assumption, we have
$x=i+jP_{\ell } \in \mathcal {I}_{\ell +1}$
. By the assumption, we have
![]() $\gcd (i, P_{\ell })=1$
, and it follows that
$\gcd (i, P_{\ell })=1$
, and it follows that
![]() $\gcd (x, P_{\ell +1})=\gcd (x,P_{\ell })\gcd (x,p_{\ell +1})=\gcd (i, P_{\ell })\gcd (x, p_{\ell +1})=1.$
This proves the claim.
$\gcd (x, P_{\ell +1})=\gcd (x,P_{\ell })\gcd (x,p_{\ell +1})=\gcd (i, P_{\ell })\gcd (x, p_{\ell +1})=1.$
This proves the claim.
Furthermore, we introduce the following notation which is similar to the previously introduced on equation (5.2). For each
![]() $\ell \geq 1$
, we let
$\ell \geq 1$
, we let
Note that
![]() $T_1=\sqrt {2}$
. We also establish a recurrence relation on the sequence.
$T_1=\sqrt {2}$
. We also establish a recurrence relation on the sequence.
Lemma 5.4 The sequence
![]() $(T_{\ell })_{\ell \geq 1}$
satisfies the recurrence relation
$(T_{\ell })_{\ell \geq 1}$
satisfies the recurrence relation
Proof We have
 $$ \begin{align*} T_{\ell+1} &=\sum_{i \in \mathcal{I}_{\ell}} \sum_{\substack{0 \leq j<p_{\ell+1}\\ p_{\ell+1} \nmid (i+j P_{\ell})}}\sqrt{\gcd(i+jP_{\ell}-1, P_{\ell+1})}\\ &=\sum_{i \in \mathcal{I}_{\ell}} \sum_{\substack{0 \leq j<p_{\ell+1}\\ p_{\ell+1} \nmid (i+j P_{\ell})}}\sqrt{\gcd(i+jP_{\ell}-1, P_{\ell})} \sqrt{\gcd(i+jP_{\ell}-1, p_{\ell+1})}\\ &=\sum_{i \in \mathcal{I}_{\ell}} \sqrt{\gcd(i-1, P_{\ell})} \bigg(\sum_{\substack{0 \leq j<p_{\ell+1}\\ p_{\ell+1} \nmid (i+j P_{\ell})}} \sqrt{\gcd(i+jP_{\ell}-1, p_{\ell+1})}\bigg). \end{align*} $$
$$ \begin{align*} T_{\ell+1} &=\sum_{i \in \mathcal{I}_{\ell}} \sum_{\substack{0 \leq j<p_{\ell+1}\\ p_{\ell+1} \nmid (i+j P_{\ell})}}\sqrt{\gcd(i+jP_{\ell}-1, P_{\ell+1})}\\ &=\sum_{i \in \mathcal{I}_{\ell}} \sum_{\substack{0 \leq j<p_{\ell+1}\\ p_{\ell+1} \nmid (i+j P_{\ell})}}\sqrt{\gcd(i+jP_{\ell}-1, P_{\ell})} \sqrt{\gcd(i+jP_{\ell}-1, p_{\ell+1})}\\ &=\sum_{i \in \mathcal{I}_{\ell}} \sqrt{\gcd(i-1, P_{\ell})} \bigg(\sum_{\substack{0 \leq j<p_{\ell+1}\\ p_{\ell+1} \nmid (i+j P_{\ell})}} \sqrt{\gcd(i+jP_{\ell}-1, p_{\ell+1})}\bigg). \end{align*} $$
It is easy to show that the inner sum consists of
![]() $(p_{\ell +1}-2)$
many
$(p_{\ell +1}-2)$
many
![]() $1$
and a single
$1$
and a single
![]() $\sqrt {p_{\ell +1}}$
. It follows that
$\sqrt {p_{\ell +1}}$
. It follows that
proving the lemma.
We are now ready to prove Theorem 1.3.
Proof of Theorem 1.3
For each n, we choose
![]() $k=k(n)=P_\ell $
, where
$k=k(n)=P_\ell $
, where
![]() $\ell =\ell (n)$
is the largest integer such that
$\ell =\ell (n)$
is the largest integer such that
![]() $\log P_\ell <c' \sqrt {\log \log n}$
. It follows that
$\log P_\ell <c' \sqrt {\log \log n}$
. It follows that
![]() $\log k=\log P_\ell \asymp \sqrt {\log \log n}$
. Thus, using equations (5.7) and (5.9), we have
$\log k=\log P_\ell \asymp \sqrt {\log \log n}$
. Thus, using equations (5.7) and (5.9), we have
 $$ \begin{align*}\eta_k \phi(k) \leq \frac{|\mathcal{I}_\ell| \phi(P_\ell)}{T_{\ell}^2} =\prod_{p \leq p_{\ell}} \frac{(p-1)^2}{(p-2+\sqrt{p})^2}. \end{align*} $$
$$ \begin{align*}\eta_k \phi(k) \leq \frac{|\mathcal{I}_\ell| \phi(P_\ell)}{T_{\ell}^2} =\prod_{p \leq p_{\ell}} \frac{(p-1)^2}{(p-2+\sqrt{p})^2}. \end{align*} $$
Note that for each prime p, it is easy to verify that
![]() $ \frac {p-1}{p-2+\sqrt {p}} \leq 1-\frac {1}{\sqrt {p}}. $
Recall that the inequality
$ \frac {p-1}{p-2+\sqrt {p}} \leq 1-\frac {1}{\sqrt {p}}. $
Recall that the inequality
![]() $e^x \geq 1+x$
holds for all real x, and a standard application of partial summation gives
$e^x \geq 1+x$
holds for all real x, and a standard application of partial summation gives
 $$ \begin{align*}\sum\limits_{p \leq x} \frac{1}{\sqrt{p}} = \frac{2\sqrt{x}}{\log x} + O\left(\frac{\sqrt{x}}{\log ^2x}\right). \end{align*} $$
$$ \begin{align*}\sum\limits_{p \leq x} \frac{1}{\sqrt{p}} = \frac{2\sqrt{x}}{\log x} + O\left(\frac{\sqrt{x}}{\log ^2x}\right). \end{align*} $$
Also, the prime number theorem implies that
and thus
![]() $p_{\ell }=(1+o(1))\log P_{\ell }$
. Putting the above estimates altogether, we have
$p_{\ell }=(1+o(1))\log P_{\ell }$
. Putting the above estimates altogether, we have
 $$ \begin{align*} \eta_k \phi(k) &\leq \prod_{p \leq p_{\ell}} \bigg(1-\frac{1}{\sqrt{p}}\bigg)^2 \leq \exp \bigg(-2\sum_{p \leq p_{\ell}} \frac{1}{\sqrt{p}}\bigg)\\ &=\exp\bigg(-\frac{(4+o(1))\sqrt{p_{\ell}}}{\log p_{\ell}}\bigg) =\exp\bigg(-\frac{(4+o(1))\sqrt{\log P_\ell}}{\log \log P_\ell}\bigg)\\ &\leq \exp\bigg(-\frac{c"(\log \log n)^{1/4}}{\log \log \log n}\bigg). \end{align*} $$
$$ \begin{align*} \eta_k \phi(k) &\leq \prod_{p \leq p_{\ell}} \bigg(1-\frac{1}{\sqrt{p}}\bigg)^2 \leq \exp \bigg(-2\sum_{p \leq p_{\ell}} \frac{1}{\sqrt{p}}\bigg)\\ &=\exp\bigg(-\frac{(4+o(1))\sqrt{p_{\ell}}}{\log p_{\ell}}\bigg) =\exp\bigg(-\frac{(4+o(1))\sqrt{\log P_\ell}}{\log \log P_\ell}\bigg)\\ &\leq \exp\bigg(-\frac{c"(\log \log n)^{1/4}}{\log \log \log n}\bigg). \end{align*} $$
for some absolute constant
![]() $c">0$
. It follows from Theorem 1.2 that
$c">0$
. It follows from Theorem 1.2 that
 $$\begin{align*}M_k(n) \ll \eta_k\phi(k) \log n \ll \exp\bigg(-\frac{c"(\log \log n)^{1/4}}{\log \log \log n}\bigg) \log n. \end{align*}$$
$$\begin{align*}M_k(n) \ll \eta_k\phi(k) \log n \ll \exp\bigg(-\frac{c"(\log \log n)^{1/4}}{\log \log \log n}\bigg) \log n. \end{align*}$$
5.3 An upper bound on
 $\eta _{k}$
$\eta _{k}$
In this subsection, we deduce a simple upper bound of
![]() $\eta _k$
. It turns out that this upper bound well approximates
$\eta _k$
. It turns out that this upper bound well approximates
![]() $\eta _k$
empirically.
$\eta _k$
empirically.
Theorem 5.5 For any
![]() $k \ge 2$
, we have
$k \ge 2$
, we have
where
![]() $\mu _{k} = R_{k} \cdot \min \{\beta (p^\alpha ): p^\alpha \vert \vert k\}$
with
$\mu _{k} = R_{k} \cdot \min \{\beta (p^\alpha ): p^\alpha \vert \vert k\}$
with
 $$\begin{align*}R_{k}=\prod_{p^{\alpha} \mid \mid k} \frac{(p-1) p^{\alpha-1}}{\big(p^{\alpha} - p^{\alpha -1} - p^{(\alpha-1)/2} + p^{\alpha -1/2}\big)^2},\end{align*}$$
$$\begin{align*}R_{k}=\prod_{p^{\alpha} \mid \mid k} \frac{(p-1) p^{\alpha-1}}{\big(p^{\alpha} - p^{\alpha -1} - p^{(\alpha-1)/2} + p^{\alpha -1/2}\big)^2},\end{align*}$$
and
 $$\begin{align*}\beta(p^\alpha) = \frac{\big(p^{\alpha} - p^{\alpha -1} - p^{(\alpha-1)/2} + p^{\alpha -1/2}\big)^2}{(p-1)\big(- p^{(\alpha-1)/2} + p^{\alpha-1} + p^{\alpha-1/2}\big)^2}.\end{align*}$$
$$\begin{align*}\beta(p^\alpha) = \frac{\big(p^{\alpha} - p^{\alpha -1} - p^{(\alpha-1)/2} + p^{\alpha -1/2}\big)^2}{(p-1)\big(- p^{(\alpha-1)/2} + p^{\alpha-1} + p^{\alpha-1/2}\big)^2}.\end{align*}$$
Proof We denote
![]() $k=\prod _{j=1}^{\ell } p_j^{\alpha _j}$
, where
$k=\prod _{j=1}^{\ell } p_j^{\alpha _j}$
, where
![]() $p_1,p_2, \ldots , p_\ell $
are distinct primes factors of k such that
$p_1,p_2, \ldots , p_\ell $
are distinct primes factors of k such that
Define
Then
![]() $\mathcal {I}$
is obviously a subset of the set
$\mathcal {I}$
is obviously a subset of the set
![]() $\{1 \leq i \leq k: \gcd (i,k)=1, \gcd (i-1,k)>1\}$
consisting of residue classes that can be used in Gallagher’s larger sieve in the proof of Theorem 1.2. (In particular, when
$\{1 \leq i \leq k: \gcd (i,k)=1, \gcd (i-1,k)>1\}$
consisting of residue classes that can be used in Gallagher’s larger sieve in the proof of Theorem 1.2. (In particular, when
![]() $p_\ell =2$
,
$p_\ell =2$
,
![]() $\mathcal {I}$
consists of all the available residue classes with
$\mathcal {I}$
consists of all the available residue classes with
![]() $|\mathcal {I}|=\phi (k)$
.) In view of the definition of
$|\mathcal {I}|=\phi (k)$
.) In view of the definition of
![]() $\eta _k$
, it suffices to show that
$\eta _k$
, it suffices to show that
 $$ \begin{align*}\frac{|\mathcal{I}|}{T_{\mathcal{I}}^2}=\mu_k=R_k \cdot \beta(p_\ell^{\alpha_\ell}).\end{align*} $$
$$ \begin{align*}\frac{|\mathcal{I}|}{T_{\mathcal{I}}^2}=\mu_k=R_k \cdot \beta(p_\ell^{\alpha_\ell}).\end{align*} $$
We first compute the size of
![]() $\mathcal {I}$
. Equivalently, we can write
$\mathcal {I}$
. Equivalently, we can write
and hence, we deduce
![]() $|\mathcal {I}|=\prod _{j=1}^{\ell -1} (p_j-1)p_j^{\alpha _j-1} \cdot p_{\ell }^{\alpha _\ell -1}$
. In order to compute
$|\mathcal {I}|=\prod _{j=1}^{\ell -1} (p_j-1)p_j^{\alpha _j-1} \cdot p_{\ell }^{\alpha _\ell -1}$
. In order to compute
![]() $T_{\mathcal {I}}$
, we first count the number of solutions to
$T_{\mathcal {I}}$
, we first count the number of solutions to
![]() $v_{p_j}(i-1)=s$
over
$v_{p_j}(i-1)=s$
over
![]() $1 \leq i \leq p_j^{\alpha _j}$
such that
$1 \leq i \leq p_j^{\alpha _j}$
such that
![]() $p_j \nmid i$
for
$p_j \nmid i$
for
![]() $0 \leq s \leq \alpha _j$
separately, and then use the Chinese remainder theorem. Set
$0 \leq s \leq \alpha _j$
separately, and then use the Chinese remainder theorem. Set
 $$ \begin{align*} C_{j,s}&=\{1 \leq i \leq p_j^{\alpha_j}: i\not\equiv 0 \quad\pmod{p_{j}},~ v_{p_j}(i-1)=s \}, \quad \text{for } 0\leq s\leq \alpha_{j}, j<\ell;\\ C_{\ell,s}&=\{1 \leq i \leq p_{\ell}^{\alpha_{\ell}}: i\equiv 1 \quad\pmod{p_{\ell}},~ v_{p_\ell}(i-1)=s \}, \quad \text{for } 0\leq s\leq \alpha_{\ell}. \end{align*} $$
$$ \begin{align*} C_{j,s}&=\{1 \leq i \leq p_j^{\alpha_j}: i\not\equiv 0 \quad\pmod{p_{j}},~ v_{p_j}(i-1)=s \}, \quad \text{for } 0\leq s\leq \alpha_{j}, j<\ell;\\ C_{\ell,s}&=\{1 \leq i \leq p_{\ell}^{\alpha_{\ell}}: i\equiv 1 \quad\pmod{p_{\ell}},~ v_{p_\ell}(i-1)=s \}, \quad \text{for } 0\leq s\leq \alpha_{\ell}. \end{align*} $$
Note that
 $$ \begin{align*} |C_{j,s}|&=\phi(p_j^{\alpha_j-s}), \quad \quad \quad \quad \!\text{for } 0<s\leq \alpha_{j}, j<\ell;\\ |C_{j,0}|&=\phi(p_j^{\alpha_j})-p_{j}^{\alpha_{j}-1}, \quad \; \; \text{for } j<\ell;\\ |C_{\ell,s}|&=\phi(p_{\ell}^{\alpha_{\ell}-s}), \quad \quad \quad \quad \!\text{for } 0<s\leq \alpha_{\ell}, \end{align*} $$
$$ \begin{align*} |C_{j,s}|&=\phi(p_j^{\alpha_j-s}), \quad \quad \quad \quad \!\text{for } 0<s\leq \alpha_{j}, j<\ell;\\ |C_{j,0}|&=\phi(p_j^{\alpha_j})-p_{j}^{\alpha_{j}-1}, \quad \; \; \text{for } j<\ell;\\ |C_{\ell,s}|&=\phi(p_{\ell}^{\alpha_{\ell}-s}), \quad \quad \quad \quad \!\text{for } 0<s\leq \alpha_{\ell}, \end{align*} $$
and
![]() $|C_{\ell ,0}|=0$
. It follows that
$|C_{\ell ,0}|=0$
. It follows that
 $$ \begin{align*} T_{\mathcal{I}}=\sum_{i \in \mathcal{I}} \sqrt{\gcd(i-1,k)}=\sum_{d \mid k} \sqrt{d} \sum_{\substack{i \in \mathcal{I},\\ \gcd(i-1,k)=d}} 1=\prod_{j=1}^{\ell}\left(\sum_{s=0}^{\alpha_{j}}\sqrt{p_{j}^{s}}|C_{j,s}|\right). \end{align*} $$
$$ \begin{align*} T_{\mathcal{I}}=\sum_{i \in \mathcal{I}} \sqrt{\gcd(i-1,k)}=\sum_{d \mid k} \sqrt{d} \sum_{\substack{i \in \mathcal{I},\\ \gcd(i-1,k)=d}} 1=\prod_{j=1}^{\ell}\left(\sum_{s=0}^{\alpha_{j}}\sqrt{p_{j}^{s}}|C_{j,s}|\right). \end{align*} $$
For each
![]() $1 \leq j \leq \ell -1$
, we calculate
$1 \leq j \leq \ell -1$
, we calculate
 $$ \begin{align*} \sum_{s=0}^{\alpha_j} \sqrt{p_j^s} |C_{j,s}| & =\phi(p_{j}^{\alpha_{j}}) - p_{j}^{\alpha_{j}-1} + \sum_{s=1}^{\alpha_{j}}\sqrt{p_{j}^s} \phi(p_{j}^{\alpha_{j}-s}) \\ &=p_{j}^{\alpha_{j}} - p_{j}^{\alpha_{j} -1} - p_{j}^{(\alpha_{j}-1)/2} + p_{j}^{\alpha_{j} -1/2}. \end{align*} $$
$$ \begin{align*} \sum_{s=0}^{\alpha_j} \sqrt{p_j^s} |C_{j,s}| & =\phi(p_{j}^{\alpha_{j}}) - p_{j}^{\alpha_{j}-1} + \sum_{s=1}^{\alpha_{j}}\sqrt{p_{j}^s} \phi(p_{j}^{\alpha_{j}-s}) \\ &=p_{j}^{\alpha_{j}} - p_{j}^{\alpha_{j} -1} - p_{j}^{(\alpha_{j}-1)/2} + p_{j}^{\alpha_{j} -1/2}. \end{align*} $$
Similarly, we have
 $$ \begin{align*} \sum_{s=0}^{\alpha_\ell} \sqrt{p_\ell^s} |C_{\ell,s}| & = \sum_{s=1}^{\alpha_\ell} \sqrt{p_\ell^s} \phi(p_\ell^{\alpha_\ell-s})= - p_{\ell}^{(\alpha_{\ell}-1)/2} + p_{\ell}^{\alpha_{\ell}-1} + p_{\ell}^{\alpha_{\ell}-1/2}. \end{align*} $$
$$ \begin{align*} \sum_{s=0}^{\alpha_\ell} \sqrt{p_\ell^s} |C_{\ell,s}| & = \sum_{s=1}^{\alpha_\ell} \sqrt{p_\ell^s} \phi(p_\ell^{\alpha_\ell-s})= - p_{\ell}^{(\alpha_{\ell}-1)/2} + p_{\ell}^{\alpha_{\ell}-1} + p_{\ell}^{\alpha_{\ell}-1/2}. \end{align*} $$
Putting these all together, we compute
 $$ \begin{align*} T_{\mathcal{I}} &=\prod_{j=1}^{\ell-1} \bigg[p_{j}^{\alpha_{j}} - p_{j}^{\alpha_{j} -1} - p_{j}^{(\alpha_{j}-1)/2} + p_{j}^{\alpha_{j} -1/2} \bigg]\cdot \bigg( - p_{\ell}^{(\alpha_{\ell}-1)/2} + p_{\ell}^{\alpha_{\ell}-1} + p_{\ell}^{\alpha_{\ell}-1/2} \bigg). \end{align*} $$
$$ \begin{align*} T_{\mathcal{I}} &=\prod_{j=1}^{\ell-1} \bigg[p_{j}^{\alpha_{j}} - p_{j}^{\alpha_{j} -1} - p_{j}^{(\alpha_{j}-1)/2} + p_{j}^{\alpha_{j} -1/2} \bigg]\cdot \bigg( - p_{\ell}^{(\alpha_{\ell}-1)/2} + p_{\ell}^{\alpha_{\ell}-1} + p_{\ell}^{\alpha_{\ell}-1/2} \bigg). \end{align*} $$
Hence,
 $$ \begin{align*} \frac{|\mathcal{I}|}{T_{\mathcal{I}}^2} &=\prod_{j=1}^{\ell-1} \frac{(p_j-1) p_j^{\alpha_j-1}}{\big(p_{j}^{\alpha_{j}} - p_{j}^{\alpha_{j} -1} - p_{j}^{(\alpha_{j}-1)/2} + p_{j}^{\alpha_{j} -1/2}\big)^2}\cdot \frac{ p_\ell^{\alpha_\ell-1}}{\big( - p_{\ell}^{(\alpha_{\ell}-1)/2} + p_{\ell}^{\alpha_{\ell}-1} + p_{\ell}^{\alpha_{\ell}-1/2}\big)^2}. \end{align*} $$
$$ \begin{align*} \frac{|\mathcal{I}|}{T_{\mathcal{I}}^2} &=\prod_{j=1}^{\ell-1} \frac{(p_j-1) p_j^{\alpha_j-1}}{\big(p_{j}^{\alpha_{j}} - p_{j}^{\alpha_{j} -1} - p_{j}^{(\alpha_{j}-1)/2} + p_{j}^{\alpha_{j} -1/2}\big)^2}\cdot \frac{ p_\ell^{\alpha_\ell-1}}{\big( - p_{\ell}^{(\alpha_{\ell}-1)/2} + p_{\ell}^{\alpha_{\ell}-1} + p_{\ell}^{\alpha_{\ell}-1/2}\big)^2}. \end{align*} $$
Therefore, Theorem 1.2 implies
Corollary 5.6 There is a constant
![]() $c'>0$
, such that as
$c'>0$
, such that as
![]() $n \to \infty $
,
$n \to \infty $
,
 $$ \begin{align*}M_k(n)\leq \bigg({\frac{2k}{k-2}}+o(1)\bigg) \ \mu_k \phi(k) \log n, \end{align*} $$
$$ \begin{align*}M_k(n)\leq \bigg({\frac{2k}{k-2}}+o(1)\bigg) \ \mu_k \phi(k) \log n, \end{align*} $$
holds uniformly for positive integers
![]() $k,n \geq 3$
such that
$k,n \geq 3$
such that
![]() $\log k \leq c'\sqrt {\log \log n}$
.
$\log k \leq c'\sqrt {\log \log n}$
.
Remark 5.7 Our computations indicate that when
![]() $2 \leq k \leq 100{,}000$
, the inequality
$2 \leq k \leq 100{,}000$
, the inequality
![]() $\mu _k \leq 2\eta _k$
holds for all but
$\mu _k \leq 2\eta _k$
holds for all but
![]() $501$
of them. This numerical evidence suggests that
$501$
of them. This numerical evidence suggests that
![]() $\mu _k$
provides a good approximation for
$\mu _k$
provides a good approximation for
![]() $\eta _k$
for a generic k. Note that the computational complexity for computing
$\eta _k$
for a generic k. Note that the computational complexity for computing
![]() $\mu _k$
is the same as that of the prime factorization of k: a naive algorithm takes
$\mu _k$
is the same as that of the prime factorization of k: a naive algorithm takes
![]() $O(\sqrt {k})$
time. The best theoretical algorithm has running time
$O(\sqrt {k})$
time. The best theoretical algorithm has running time
![]() $O\big (\exp ((\log k)^{1/3+o(1)})\big )$
using the general number field sieve [Reference Buhler, Lenstra and Pomerance5]. On the other hand, computing
$O\big (\exp ((\log k)^{1/3+o(1)})\big )$
using the general number field sieve [Reference Buhler, Lenstra and Pomerance5]. On the other hand, computing
![]() $\eta _k$
requires
$\eta _k$
requires
![]() $O(k\log k)$
time; we refer to Appendix A for an algorithm and some computational results.
$O(k\log k)$
time; we refer to Appendix A for an algorithm and some computational results.
6 Multiplicative decompositions of shifted multiplicative subgroups
In this section, we present our contributions to Conjecture 1.9. In particular, we make significant progress toward Sárközy’s conjecture (Conjecture 1.8). We recall
![]() $S_d=S_d({\mathbb F}_q)=\{x^d: x \in {\mathbb F}_q^*\}$
.
$S_d=S_d({\mathbb F}_q)=\{x^d: x \in {\mathbb F}_q^*\}$
.
6.1 Applications to Sárközy’s conjecture
In this subsection, we show that for almost all primes
![]() $p \equiv 1 \ \pmod d$
, the set
$p \equiv 1 \ \pmod d$
, the set
![]() $(S_d({\mathbb F}_p)-1) \setminus \{0\}$
cannot be decomposed as the product of two sets non-trivially. This confirms the truth of Sárközy’s conjecture (Conjecture 1.8) as well as the truth of its generalization in the generic case (Conjecture 1.9) when the shift of the subgroup is given by
$(S_d({\mathbb F}_p)-1) \setminus \{0\}$
cannot be decomposed as the product of two sets non-trivially. This confirms the truth of Sárközy’s conjecture (Conjecture 1.8) as well as the truth of its generalization in the generic case (Conjecture 1.9) when the shift of the subgroup is given by
![]() $\lambda =1$
.
$\lambda =1$
.
Theorem 6.1 Let
![]() $d \geq 2$
be fixed. As
$d \geq 2$
be fixed. As
![]() $x \to \infty $
, the number of primes
$x \to \infty $
, the number of primes
![]() $p \leq x$
such that
$p \leq x$
such that
![]() $p \equiv 1 \ \pmod d$
and
$p \equiv 1 \ \pmod d$
and
![]() $(S_d({\mathbb F}_p)-1) \setminus \{0\}$
can be decomposed as the product of two sets non-trivially (that is, it can be written as the product of two subsets of
$(S_d({\mathbb F}_p)-1) \setminus \{0\}$
can be decomposed as the product of two sets non-trivially (that is, it can be written as the product of two subsets of
![]() ${\mathbb F}_p^*$
with size at least 2) is
${\mathbb F}_p^*$
with size at least 2) is
![]() $o(\pi (x))$
.
$o(\pi (x))$
.
Proof Let
![]() $\mathcal {P}_d$
be the set of primes p such that
$\mathcal {P}_d$
be the set of primes p such that
![]() $p \equiv 1 \ \pmod d$
and
$p \equiv 1 \ \pmod d$
and
![]() $(S_d({\mathbb F}_p)-1) \setminus \{0\}$
admits a non-trivial multiplicative decomposition. By the prime number theorem for arithmetic progressions, it suffices to show that
$(S_d({\mathbb F}_p)-1) \setminus \{0\}$
admits a non-trivial multiplicative decomposition. By the prime number theorem for arithmetic progressions, it suffices to show that
![]() $|\mathcal {P}_d \cap [0,x]|=o(x/\log x)$
.
$|\mathcal {P}_d \cap [0,x]|=o(x/\log x)$
.
Let
![]() $p \in \mathcal {P}_d$
. Then we can write
$p \in \mathcal {P}_d$
. Then we can write
![]() $(S_d-1) \setminus \{0\}$
as the product of two sets
$(S_d-1) \setminus \{0\}$
as the product of two sets
![]() $A,B \subset {\mathbb F}_p^*$
such that
$A,B \subset {\mathbb F}_p^*$
such that
![]() $|A|, |B| \geq 2$
. Then Corollary 1.10 implies that
$|A|, |B| \geq 2$
. Then Corollary 1.10 implies that
![]() $|A||B|=\frac {p-1}{d}-1,$
that is,
$|A||B|=\frac {p-1}{d}-1,$
that is,
On the other hand, Proposition 3.4 implies that we can find an absolute constant
![]() $C_d \in (0,1)$
such that
$C_d \in (0,1)$
such that
It follows that
![]() $p-(d+1)$
has a divisor in the interval
$p-(d+1)$
has a divisor in the interval
![]() $(C_d\sqrt {p}, \sqrt {p})$
. To summarize, if
$(C_d\sqrt {p}, \sqrt {p})$
. To summarize, if
![]() $p \in \mathcal {P}_d$
, then we have
$p \in \mathcal {P}_d$
, then we have
![]() $\tau (p-(d+1);C_d\sqrt {p},\sqrt {p}) \geq 1,$
where
$\tau (p-(d+1);C_d\sqrt {p},\sqrt {p}) \geq 1,$
where
![]() $\tau (n;y,z)$
denotes the number of divisors of n in the interval
$\tau (n;y,z)$
denotes the number of divisors of n in the interval
![]() $(y,z]$
. Now, we use results by Ford [Reference Ford14, Theorem 6] on the distribution of shift primes with a divisor in a given interval. Denote
$(y,z]$
. Now, we use results by Ford [Reference Ford14, Theorem 6] on the distribution of shift primes with a divisor in a given interval. Denote
Setting
![]() $y=C_d\sqrt {x}/2$
and
$y=C_d\sqrt {x}/2$
and
![]() $z=\sqrt {x}$
, [Reference Ford14, Theorem 6] and [Reference Ford14, Theorem 1, third case of (v)] imply that
$z=\sqrt {x}$
, [Reference Ford14, Theorem 6] and [Reference Ford14, Theorem 1, third case of (v)] imply that
 $$ \begin{align*}P_d(x,y,z) \ll \frac{H(x,y,z)}{\log x} \ll \frac{x}{\log x} u^\delta \bigg(\log \frac{2}{u}\bigg)^{-3/2} \end{align*} $$
$$ \begin{align*}P_d(x,y,z) \ll \frac{H(x,y,z)}{\log x} \ll \frac{x}{\log x} u^\delta \bigg(\log \frac{2}{u}\bigg)^{-3/2} \end{align*} $$
where
![]() $\delta =1-\frac {1+\log \log 2}{\log 2}$
and
$\delta =1-\frac {1+\log \log 2}{\log 2}$
and
![]() $u=\log (C_d/2)/\log y$
. It follows that as
$u=\log (C_d/2)/\log y$
. It follows that as
![]() $x \to \infty $
, we have
$x \to \infty $
, we have
![]() $P_d(x,y,z)=o(x/\log x)$
. Therefore, we have
$P_d(x,y,z)=o(x/\log x)$
. Therefore, we have
 $$ \begin{align*}\#\{p \in \mathcal{P}_d: x/2\leq p\leq x\} & \leq \#\{x/2\leq p\leq x: \tau (p-(d+1); C_d\sqrt{x}/2,\sqrt{x}) \geq 1\} \\ &=o(x/\log x). \end{align*} $$
$$ \begin{align*}\#\{p \in \mathcal{P}_d: x/2\leq p\leq x\} & \leq \#\{x/2\leq p\leq x: \tau (p-(d+1); C_d\sqrt{x}/2,\sqrt{x}) \geq 1\} \\ &=o(x/\log x). \end{align*} $$
We conclude that as
![]() $x \to \infty $
,
$x \to \infty $
,
 $$ \begin{align*} |\mathcal{P}_d \cap [0,x]| &=O(\sqrt{x})+\#\{p \in \mathcal{P}_d: \sqrt{x}\leq p\leq x\}\\ &=O(\sqrt{x})+\sum_{0\leq j \leq (\log_2 x)/2} o\bigg(\frac{x/2^j}{\log (x/2^j)}\bigg)\\ &=O(\sqrt{x})+\bigg(\sum_{0\leq j \leq (\log_2 x)/2} \frac{1}{2^j}\bigg)o\bigg(\frac{x}{\log x}\bigg) =o\bigg(\frac{x}{\log x}\bigg). \end{align*} $$
$$ \begin{align*} |\mathcal{P}_d \cap [0,x]| &=O(\sqrt{x})+\#\{p \in \mathcal{P}_d: \sqrt{x}\leq p\leq x\}\\ &=O(\sqrt{x})+\sum_{0\leq j \leq (\log_2 x)/2} o\bigg(\frac{x/2^j}{\log (x/2^j)}\bigg)\\ &=O(\sqrt{x})+\bigg(\sum_{0\leq j \leq (\log_2 x)/2} \frac{1}{2^j}\bigg)o\bigg(\frac{x}{\log x}\bigg) =o\bigg(\frac{x}{\log x}\bigg). \end{align*} $$
Using a similar argument, we can prove Theorem 1.11.
Proof of Theorem 1.11
Consider the family of primes p such that
![]() $p \equiv 1 \ \pmod d$
and n is a dth power modulo p. By a standard application of the Chebotarev density theorem, the density of such primes is given by
$p \equiv 1 \ \pmod d$
and n is a dth power modulo p. By a standard application of the Chebotarev density theorem, the density of such primes is given by
![]() $\frac {1}{[\mathbb {Q}(e^{2\pi i/d}, n^{1/d}):\mathbb {Q}]}$
. Among the family of such primes p, we can repeat the same argument as in the proof of Theorem 6.1 to show that if
$\frac {1}{[\mathbb {Q}(e^{2\pi i/d}, n^{1/d}):\mathbb {Q}]}$
. Among the family of such primes p, we can repeat the same argument as in the proof of Theorem 6.1 to show that if
![]() $(S_d({\mathbb F}_p)-n) \setminus \{0\}$
admits a non-trivial multiplicative decomposition, then
$(S_d({\mathbb F}_p)-n) \setminus \{0\}$
admits a non-trivial multiplicative decomposition, then
![]() $p-(d+1)$
necessarily has a divisor which is “close to”
$p-(d+1)$
necessarily has a divisor which is “close to”
![]() $\sqrt {p}$
. We remark that it is important to assume that n is a dth power modulo p, so that we can take advantage of Corollary 1.10. Similar to the proof of Theorem 6.1, we can show that among the family of primes
$\sqrt {p}$
. We remark that it is important to assume that n is a dth power modulo p, so that we can take advantage of Corollary 1.10. Similar to the proof of Theorem 6.1, we can show that among the family of primes
![]() $p \equiv 1 \ \pmod d$
, the property that
$p \equiv 1 \ \pmod d$
, the property that
![]() $p-(d+1)$
has a divisor with the desired magnitude fails to hold for almost all p. This finishes the proof of the theorem.
$p-(d+1)$
has a divisor with the desired magnitude fails to hold for almost all p. This finishes the proof of the theorem.
Remark 6.2 When n is a fixed negative integer, one can obtain a similar result to Theorem 1.11 following the idea of the above proof.
Remark 6.3 Theorem 1.11 essentially states if d is fixed,
![]() $p \equiv 1 \ \pmod d$
is a prime, and
$p \equiv 1 \ \pmod d$
is a prime, and
![]() $\lambda \in S_d({\mathbb F}_p)$
, then it is very unlikely that we can decompose
$\lambda \in S_d({\mathbb F}_p)$
, then it is very unlikely that we can decompose
![]() $(S_d({\mathbb F}_p)-\lambda )\setminus \{0\}$
as the product of two subsets of
$(S_d({\mathbb F}_p)-\lambda )\setminus \{0\}$
as the product of two subsets of
![]() ${\mathbb F}_p^*$
non-trivially. On the other hand, when
${\mathbb F}_p^*$
non-trivially. On the other hand, when
![]() $\lambda \notin S_d({\mathbb F}_p)$
, the above technique does not apply. Nevertheless, when
$\lambda \notin S_d({\mathbb F}_p)$
, the above technique does not apply. Nevertheless, when
![]() $\lambda \notin S_d$
and we have two sets
$\lambda \notin S_d$
and we have two sets
![]() $A,B \subset {\mathbb F}_p^*$
such that
$A,B \subset {\mathbb F}_p^*$
such that
![]() $AB=(S_d-\lambda ) \setminus \{0\}=S_d-\lambda $
, Theorem 1.1 implies that
$AB=(S_d-\lambda ) \setminus \{0\}=S_d-\lambda $
, Theorem 1.1 implies that
In particular, we get the following non-trivial fact: if
![]() $|A|$
is fixed, then
$|A|$
is fixed, then
![]() $|B|$
is also uniquely fixed.
$|B|$
is also uniquely fixed.
6.2 Applications to special multiplicative decompositions
In this subsection, we verify the ternary version of Conjecture 1.9 in a strong sense, which generalizes [Reference Sárközy31, Theorem 2].
Shkredov [Reference Shkredov33, Theorem 3] showed if G is a multiplicative subgroup of
![]() ${\mathbb F}_p$
with
${\mathbb F}_p$
with
![]() $1 \ll _{\epsilon } |G| \leq p^{6/7-\epsilon }$
, then there is no
$1 \ll _{\epsilon } |G| \leq p^{6/7-\epsilon }$
, then there is no
![]() $A \subset {\mathbb F}_p$
and
$A \subset {\mathbb F}_p$
and
![]() $\xi \in {\mathbb F}_p^*$
such that
$\xi \in {\mathbb F}_p^*$
such that
![]() $A/A=\xi G+1$
. In fact, due to the analytic nature of the proof, he pointed out that his proof can be slightly modified to show something stronger, namely
$A/A=\xi G+1$
. In fact, due to the analytic nature of the proof, he pointed out that his proof can be slightly modified to show something stronger, namely
![]() $A/A \neq (\xi G+1) \cup C$
, as long as C is small (see also [Reference Shkredov33, Remark 15]). The following corollary of Theorem 1.1 is of a similar flavor.
$A/A \neq (\xi G+1) \cup C$
, as long as C is small (see also [Reference Shkredov33, Remark 15]). The following corollary of Theorem 1.1 is of a similar flavor.
Corollary 6.4 Let p be a prime. If G is a proper multiplicative subgroup of
![]() ${\mathbb F}_p$
with
${\mathbb F}_p$
with
![]() $|G|\geq 8$
, and
$|G|\geq 8$
, and
![]() $\lambda , \xi \in {\mathbb F}_p^*$
, then there is no
$\lambda , \xi \in {\mathbb F}_p^*$
, then there is no
![]() $A \subset {\mathbb F}_p^*$
such that
$A \subset {\mathbb F}_p^*$
such that
![]() $AA=(\xi G-\lambda ) \setminus \{0\}$
.
$AA=(\xi G-\lambda ) \setminus \{0\}$
.
Proof We assume, otherwise, that
![]() $AA=(\xi G-\lambda ) \setminus \{0\}$
for some
$AA=(\xi G-\lambda ) \setminus \{0\}$
for some
![]() $A\subset \mathbb {F}_p^{*}$
. Then we observe that
$A\subset \mathbb {F}_p^{*}$
. Then we observe that
![]() $aa'=a'a$
for each
$aa'=a'a$
for each
![]() $a,a' \in A$
, it follows that
$a,a' \in A$
, it follows that
Since
![]() $|G| \geq 8$
, it follows that
$|G| \geq 8$
, it follows that
![]() $|A| \geq 4$
. Let
$|A| \geq 4$
. Let
![]() $B=A/\xi $
, and
$B=A/\xi $
, and
![]() $\lambda '=\lambda /\xi $
. Then we have
$\lambda '=\lambda /\xi $
. Then we have
![]() $AB=(G-\lambda ')\setminus \{0\}$
and thus Theorem 1.1 implies that
$AB=(G-\lambda ')\setminus \{0\}$
and thus Theorem 1.1 implies that
![]() $|A|^2=|A||B|\leq |G|+|A|-1$
. Comparing the above two inequalities, we obtain that
$|A|^2=|A||B|\leq |G|+|A|-1$
. Comparing the above two inequalities, we obtain that
which implies that
![]() $|A|\leq 3$
, contradicting the assumption that
$|A|\leq 3$
, contradicting the assumption that
![]() $|A| \geq 4$
.
$|A| \geq 4$
.
Lemma 6.5 Let
![]() $A, B, C$
be nonempty subsets of
$A, B, C$
be nonempty subsets of
![]() ${\mathbb F}_q$
and let
${\mathbb F}_q$
and let
![]() $\lambda \in {\mathbb F}_q^*$
. Then
$\lambda \in {\mathbb F}_q^*$
. Then
![]() $|ABC+\lambda |^2 \leq |AB+\lambda ||BC+\lambda ||CA+\lambda |$
.
$|ABC+\lambda |^2 \leq |AB+\lambda ||BC+\lambda ||CA+\lambda |$
.
Proof It suffices to show
![]() $|ABC|^2 \leq |AB||BC||CA|$
, which is a special case of [Reference Ruzsa29, Theorem 5.1] due to Ruzsa.
$|ABC|^2 \leq |AB||BC||CA|$
, which is a special case of [Reference Ruzsa29, Theorem 5.1] due to Ruzsa.
The following two theorems generalize Sárközy [Reference Sárközy31, Theorem 2] and confirm the ternary version of Conjecture 1.9 in a strong form.
Theorem 6.6 There exists an absolute constant
![]() $M>0$
, such that whenever p is a prime, G is a proper multiplicative subgroup of
$M>0$
, such that whenever p is a prime, G is a proper multiplicative subgroup of
![]() ${\mathbb F}_p$
with
${\mathbb F}_p$
with
![]() $|G|>M$
, and
$|G|>M$
, and
![]() $\lambda \in {\mathbb F}_p^*$
, there is no ternary multiplicative decomposition
$\lambda \in {\mathbb F}_p^*$
, there is no ternary multiplicative decomposition
![]() $ABC=(G-\lambda )\setminus \{0\}$
with
$ABC=(G-\lambda )\setminus \{0\}$
with
![]() $A,B,C \subset {\mathbb F}_p^*$
and
$A,B,C \subset {\mathbb F}_p^*$
and
![]() $|A|,|B|,|C| \geq 2$
.
$|A|,|B|,|C| \geq 2$
.
Proof Assume that there are sets
![]() $A,B,C \subset {\mathbb F}_p^*$
with
$A,B,C \subset {\mathbb F}_p^*$
with
![]() $|A|,|B|,|C| \geq 2$
, such that
$|A|,|B|,|C| \geq 2$
, such that
![]() $ABC=(G-\lambda )\setminus \{0\}$
for some proper multiplicative subgroup G of
$ABC=(G-\lambda )\setminus \{0\}$
for some proper multiplicative subgroup G of
![]() ${\mathbb F}_p$
and some
${\mathbb F}_p$
and some
![]() $\lambda \in {\mathbb F}_p^*$
.
$\lambda \in {\mathbb F}_p^*$
.
Then we can write
![]() $(G-\lambda )\setminus \{0\}$
in three different ways:
$(G-\lambda )\setminus \{0\}$
in three different ways:
![]() $A(BC), B(CA), C(AB)$
, so that we can apply the results in previous sections to each of them. Note that Lemma 3.6 implies that
$A(BC), B(CA), C(AB)$
, so that we can apply the results in previous sections to each of them. Note that Lemma 3.6 implies that
On the other hand, Theorem 1.1 implies that
Therefore, from Lemma 6.5 and the fact
![]() $|ABC| \in \{|G|, |G|-1\}$
, we have
$|ABC| \in \{|G|, |G|-1\}$
, we have
It follows that
that is,
![]() $|G|\ll 1$
, where the implicit constant is absolute. This completes the proof of the theorem.
$|G|\ll 1$
, where the implicit constant is absolute. This completes the proof of the theorem.
Theorem 6.7 Let
![]() $\epsilon>0$
. There is a constant
$\epsilon>0$
. There is a constant
![]() $Q=Q(\epsilon )$
, such that for each prime power
$Q=Q(\epsilon )$
, such that for each prime power
![]() $q>Q$
and a divisor d of
$q>Q$
and a divisor d of
![]() $q-1$
with
$q-1$
with
![]() $2 \leq d \leq q^{1/10-\epsilon }$
, there is no ternary multiplicative decomposition
$2 \leq d \leq q^{1/10-\epsilon }$
, there is no ternary multiplicative decomposition
![]() $ABC=(S_d({\mathbb F}_q)-\lambda )\setminus \{0\}$
with
$ABC=(S_d({\mathbb F}_q)-\lambda )\setminus \{0\}$
with
![]() $A,B,C \subset {\mathbb F}_q^*$
,
$A,B,C \subset {\mathbb F}_q^*$
,
![]() $|A|,|B|,|C| \geq 2$
, and
$|A|,|B|,|C| \geq 2$
, and
![]() $\lambda \in {\mathbb F}_q^*$
.
$\lambda \in {\mathbb F}_q^*$
.
Proof The proof is similar to the proof of Theorem 6.6. While Lemma 3.6 does not hold in the new setting (see Remark 3.8), we can instead use Proposition 3.4. If
![]() $ABC=(S_d({\mathbb F}_q)-\lambda )\setminus \{0\}$
, then Proposition 3.4 implies that
$ABC=(S_d({\mathbb F}_q)-\lambda )\setminus \{0\}$
, then Proposition 3.4 implies that
A similar computation leads to
![]() $d \gg q^{1/10}$
, which implies that
$d \gg q^{1/10}$
, which implies that
![]() $q \ll _{\epsilon } 1$
since we assume that
$q \ll _{\epsilon } 1$
since we assume that
![]() $d \leq q^{1/10-\epsilon }$
.
$d \leq q^{1/10-\epsilon }$
.
A Algorithm and Computations
We continue our discussion from the introduction on the following constant
 $$ \begin{align*}\gamma_k=\limsup_{n \to \infty} \frac{M_k(n)}{\log n}.\end{align*} $$
$$ \begin{align*}\gamma_k=\limsup_{n \to \infty} \frac{M_k(n)}{\log n}.\end{align*} $$
It is implicit in [Reference Dixit, Kim and Murty7] that
![]() $\gamma _k\leq 3 \phi (k)$
. We also write
$\gamma _k\leq 3 \phi (k)$
. We also write
![]() $\nu _{k} = \frac {2k}{k-2} \eta _k \phi (k).$
$\nu _{k} = \frac {2k}{k-2} \eta _k \phi (k).$

Figure A.1: Comparison between the new bound
![]() $\nu _k$
and the bound
$\nu _k$
and the bound
![]() $3\phi (k)$
in [Reference Dixit, Kim and Murty7] when
$3\phi (k)$
in [Reference Dixit, Kim and Murty7] when
![]() $2 \le k \le 1000$
. The black dots denote
$2 \le k \le 1000$
. The black dots denote
![]() $3\phi (k)$
, and the blue dots denote
$3\phi (k)$
, and the blue dots denote
![]() $\nu _k$
.
$\nu _k$
.
Table A.1: The minimum
![]() $m_{k}$
of the upper bounds
$m_{k}$
of the upper bounds
![]() $\{\nu _{i} \colon 1 \le i \le k\}$
for
$\{\nu _{i} \colon 1 \le i \le k\}$
for
![]() $2 \le k \leq 1{,}000{,}000$
.
$2 \le k \leq 1{,}000{,}000$
.

Table A.2: The upper bound
![]() $\nu _k$
of
$\nu _k$
of
![]() $\gamma _k$
when
$\gamma _k$
when
![]() $2 \le k \le 201$
.
$2 \le k \le 201$
.

Our main result, Theorem 1.2, implies that
![]() $\gamma _{k} \le \nu _{k}$
. In particular, in view of Remark 5.1, it follows that
$\gamma _{k} \le \nu _{k}$
. In particular, in view of Remark 5.1, it follows that
![]() $\gamma _k \leq 6$
for all
$\gamma _k \leq 6$
for all
![]() $k \geq 2$
and
$k \geq 2$
and
![]() $\gamma _k\leq 2+o(1)$
when
$\gamma _k\leq 2+o(1)$
when
![]() $k \to \infty $
. In Figure A.1, we pictorially compare our new bound
$k \to \infty $
. In Figure A.1, we pictorially compare our new bound
![]() $\nu _{k}$
with the bound
$\nu _{k}$
with the bound
![]() $3 \phi (k)$
when
$3 \phi (k)$
when
![]() $2 \le k \le 1000$
.
$2 \le k \le 1000$
.
Recall that for
![]() $k \ge 2$
, we defined the constant
$k \ge 2$
, we defined the constant
![]() $\eta _k=\underset {\mathcal {I}}{\min } |\mathcal {I}|/T_{\mathcal {I}}^2,$
where the minimum is taken over all nonempty subsets
$\eta _k=\underset {\mathcal {I}}{\min } |\mathcal {I}|/T_{\mathcal {I}}^2,$
where the minimum is taken over all nonempty subsets
![]() $\mathcal {I}$
of
$\mathcal {I}$
of
![]() $\{1 \leq i \leq k: \gcd (i,k)=1, \gcd (i-1,k)>1\},$
and
$\{1 \leq i \leq k: \gcd (i,k)=1, \gcd (i-1,k)>1\},$
and
![]() $T_{\mathcal {I}}=\sum _{i \in \mathcal {I}} \sqrt {\gcd (i-1,k)}.$
$T_{\mathcal {I}}=\sum _{i \in \mathcal {I}} \sqrt {\gcd (i-1,k)}.$
To compute
![]() $\eta _k$
, we use the following simple greedy algorithm with running time
$\eta _k$
, we use the following simple greedy algorithm with running time
![]() $O(k \log k)$
. The observation is as follows. If
$O(k \log k)$
. The observation is as follows. If
![]() $|\mathcal {I}|$
is fixed, our goal is to minimize
$|\mathcal {I}|$
is fixed, our goal is to minimize
![]() $|\mathcal {I}|/T_{\mathcal {I}}^2$
. Thus, we should choose those residue classes
$|\mathcal {I}|/T_{\mathcal {I}}^2$
. Thus, we should choose those residue classes
![]() $i \ \pmod k$
with
$i \ \pmod k$
with
![]() $\gcd (i-1,k)$
as large as possible to maximize
$\gcd (i-1,k)$
as large as possible to maximize
![]() $T_{\mathcal {I}}$
. Then, we can sort these gcds in decreasing order, and when
$T_{\mathcal {I}}$
. Then, we can sort these gcds in decreasing order, and when
![]() $|\mathcal {I}|$
is fixed, we pick those residue classes corresponding to the largest
$|\mathcal {I}|$
is fixed, we pick those residue classes corresponding to the largest
![]() $|\mathcal {I}|$
gcds. The following is a precise description of the algorithm.
$|\mathcal {I}|$
gcds. The following is a precise description of the algorithm.
Algorithm A.1 Let
![]() $k \ge 2$
. We follow the notations defined in Section 5.2.
$k \ge 2$
. We follow the notations defined in Section 5.2.
-
Step 1. Let
 $\mathcal {A}=\{1 \leq i \leq k: \gcd (i,k)=1, \gcd (i-1,k)>1\}$
. We list the elements of
$\mathcal {A}=\{1 \leq i \leq k: \gcd (i,k)=1, \gcd (i-1,k)>1\}$
. We list the elements of
 $\mathcal {A}$
by
$\mathcal {A}$
by
 $\{a_{1},a_{2},\ldots \}$
such that
$\{a_{1},a_{2},\ldots \}$
such that
 $\gcd (a_j -1,k)$
is decreasing by using a sorting algorithm.
$\gcd (a_j -1,k)$
is decreasing by using a sorting algorithm. -
Step 2. Set
 $I_{r}=\{a_{1},\ldots ,a_{r}\}$
,
$I_{r}=\{a_{1},\ldots ,a_{r}\}$
,
 $T_{I_{r}}=\sum _{i \in I_{r}} \sqrt {\gcd (i-1,k)}$
, and
$T_{I_{r}}=\sum _{i \in I_{r}} \sqrt {\gcd (i-1,k)}$
, and
 $\xi _{I_r}=|I_r|/T_{I_r}^2$
.
$\xi _{I_r}=|I_r|/T_{I_r}^2$
. -
Step 3. Return
 $\eta _{k}=\min _{r}\xi _{I_r}$
and terminate the algorithm.
$\eta _{k}=\min _{r}\xi _{I_r}$
and terminate the algorithm.
Note that the running time of the above algorithm is
![]() $O(k \log k)$
: sorting takes
$O(k \log k)$
: sorting takes
![]() $O(k \log k)$
time, while other steps take linear time.
$O(k \log k)$
time, while other steps take linear time.
Next, we also consider the minimum value
![]() $m_{k}$
of the upper bounds
$m_{k}$
of the upper bounds
![]() $\{ \nu _{i} \colon 2 \le i \le k\}$
for each
$\{ \nu _{i} \colon 2 \le i \le k\}$
for each
![]() $k \ge 2$
. Table A.1 shows the values of
$k \ge 2$
. Table A.1 shows the values of
![]() $m_{k}$
for
$m_{k}$
for
![]() $2 \le k \leq 1{,}000{,}000$
when they are changed.
$2 \le k \leq 1{,}000{,}000$
when they are changed.
We also report our computations on
![]() $\nu _k$
for
$\nu _k$
for
![]() $2 \leq k \leq 201$
in the following table.
$2 \leq k \leq 201$
in the following table.
Acknowledgements
The authors thank Andrej Dujella, Greg Martin, and József Solymosi for helpful discussions.