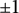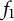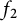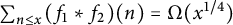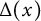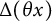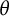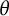1 Introduction
1.1 Main result and background
A question posed by Erdős in [Reference Erdős7], known as the Erdős discrepancy problem, states that whether for all arithmetic functions
$f:\mathbb {N}\to \{-1,1\}$
, we have that the discrepancy
$$ \begin{align} \sup_{x,d}\left|\sum_{n\leq x}f(nd)\right|=\infty. \end{align} $$
When, in addition, f is assumed to be completely multiplicative, then this reduces to whether f has unbounded partial sums.
In 2015, Tao [Reference Tao17] proved that (1.1) holds for all
$f:\mathbb {N}\to \{-1,1\}$
, and a key point of its proof is that it is sufficient to establish (1.1) only in the class of completely multiplicative functions f taking values in the unit (complex) circle.
When
$f:\mathbb {N}\to \{-1,1\}$
is assumed to be only multiplicative, then not necessarily f has unbounded partial sums. For example,
$f(n)=(-1)^{n+1}$
is multiplicative and clearly has bounded partial sums. In this case,
$f(2^k)=-1$
for all positive integers k. It was observed by Coons [Reference Coons6] that, for bounded partial sums, this rigidity on powers of
$2$
is actually necessary under suitable conditions on the values that a multiplicative function f takes at the remaining primes. Later, in the same paper [Reference Tao17], Tao gave a partial classification of multiplicative functions taking values
$\pm 1$
with bounded partial sums: They must satisfy the previous rigidity condition on powers of
$2$
, and they must be
$1$
-pretentious (for more on pretentious Number Theory, we refer the reader to [Reference Granville and Soundararajan8] by Granville and Soundararajan); that is,
$$ \begin{align*}\sum_{p}\frac{1-f(p)}{p}<\infty.\end{align*} $$
Later, Klurman [Reference Klurman12] proved that the only multiplicative functions f taking
$\pm 1$
values and with bounded partial sums are the periodic multiplicative functions with sum
$0$
inside each period, thus closing this problem for
$\pm 1$
multiplicative functions.
Building upon the referred work of Klurman, the first author proved in [Reference Aymone1] that if we allow values outside the unit disk, a M-periodic multiplicative function f with bounded partial sums such that
$f(M)\neq 0$
satisfies
-
i. For some prime
$q|M$
,
$\sum _{k=0}^\infty \frac {f(q^k)}{q^k}=0$
. -
ii. For each
$p^a\| M$
,
$f(p^k)=f(p^a)$
for all
$k\geq a$
. -
iii. For each
$\gcd (p,M)=1$
,
$f(p^k)=1$
, for all
$k\geq 1$
.
Conversely, if
$f:\mathbb {N}\to \mathbb {C}$
is multiplicative and the three conditions above are satisfied, then f has period M and has bounded partial sums. Therefore, these three conditions above give examples of multiplicative functions with values outside the unit disk with bounded partial sums, despite the fact that
$f(M)$
is zero or not.
Remark 1.1 It is interesting to observe that when it is assumed that
$|f|\leq 1$
, the only way to achieve condition i. is with
$q=2$
and
$f(2^k)=-1$
for all
$k\geq 1$
.
Remark 1.2 What makes the difference between a multiplicative function f satisfying i-ii-iii from a nonprincipal Dirichlet character
$\chi $
is that
$\chi $
neither satisfies i. nor iii.
Here, we are interested in the convolution
$f_1\ast f_2(n):=\sum _{d|n}f_1(d)f_2(n/d)$
for
$f_1$
and
$f_2$
satisfying i-ii-iii above. It was proved in [Reference Aymone1] that
$$ \begin{align*} \sum_{n\leq x}(f_1\ast f_2)(n)\ll x^{\alpha+\epsilon}, \end{align*} $$
where
$\alpha $
is the infimum over the exponents
$a>0$
such that
$\Delta (x)\ll x^{a}$
, where
$\Delta (x)$
is the classical error term in the Dirichlet divisor problem defined by
$$ \begin{align*} \sum_{n\leq x}\tau(n)=x\log x +(2\gamma-1)x+\Delta(x). \end{align*} $$
It is widely believed that
$\alpha =1/4$
, and many results were proven in this direction. The best upper bound up to date is due to Huxley [Reference Huxley9]:
$\alpha \leq 131/416 \approx 0.315$
. Regarding
$\Omega $
bounds, Soundararajan [Reference Soundararajan16] proved that
$$ \begin{align*}\Delta(x)=\Omega\left((x\log x)^{1/4}\frac{(\log\log x)^{3/4(2^{4/3}-1)}}{(\log\log\log x)^{5/8}}\right).\end{align*} $$
It was conjectured in [Reference Aymone1] that the partial sums of
$f_1\ast f_2$
obey a similar
$\Omega $
-bound for
$\Delta (x)$
; that is,
$\sum _{n\leq x}(f_1\ast f_2)(n)=\Omega (x^{1/4})$
. Here, we establish this conjecture.
Theorem 1.3 Let
$f_1$
and
$f_2$
be periodic multiplicative functions satisfying i-ii-iii above. Then
$ \sum _{n\leq x}(f_1\ast f_2)(n)=\Omega (x^{1/4})$
.
Example 1.4 The results from [Reference Aymone1] give that for each prime q, there exists a unique q-periodic multiplicative function f with bounded partial sums and such that
$f(q)\neq 0$
. In the case
$q=2$
, the corresponding function is
$f(n)=(-1)^{n+1}$
. Therefore, in this particular case, we have that
$\sum _{n\leq x}(f\ast f)(n)=\Omega (x^{1/4})$
. In particular, this establishes the conjecture in an uncovered case by Proposition 3.1 of [Reference Aymone1].
Remark 1.5 Another class of periodic multiplicative functions with bounded partial sums is that of the nonprincipal Dirichlet characters. In a forthcoming work, the first author is finishing a study where he shows a similar
$\Omega $
-bound for the partial sums of the convolution between these Dirichlet characters.
Our proof relies on two ingredients. The second one is a study of a family of quadratic forms and is explained in Section 5. The first ingredient is a generalization of a result of Tong [Reference Tong18] and proves the next theorem.
Theorem 1.6 When a and b are nonnegative integers,
$\lambda =\gcd (a,b)$
,
$c=a/\lambda $
and
$d=b/\lambda $
, we have
$$ \begin{align*} \lim_{X\to\infty}\frac{1}{X^{3/2}}\int_{1}^X \Delta(x/a)\Delta(x/b)dx=\frac{\tau(cd)}{6\pi^2\sqrt{\lambda}cd} \frac{\zeta(3/2)^4}{\zeta(3)} \prod_{p^k\|cd}\frac{1-\frac{k-1}{(k+1)p^{3/2}}}{1+1/p^{3/2}}. \end{align*} $$
Furthermore, when
$\theta>0$
is irrational, we have
$$ \begin{align*} \lim_{X\to\infty}\frac{1}{X^{3/2}}\int_{1}^X \Delta(x)\Delta(\theta x)dx=0. \end{align*} $$
1.2 The proof in the large
To prove Theorem 1.3, our starting point is the following formula from [Reference Aymone1]: If
$M_1$
and
$M_2$
are the periods of
$f_1$
and
$f_2$
, respectively, then
$$ \begin{align} \sum_{n\leq x}(f_1\ast f_2)(n)=\sum_{n|M_1M_2}(f_1\ast f_2\ast \mu \ast \mu)(n)\Delta(x/n), \end{align} $$
where
$\mu $
is the Möbius function. Therefore, the partial sums of
$f_1\ast f_2$
can be written as a finite linear combination of the quantities
$(\Delta (x/n))_n$
. Apart from the fact that
$\Delta (x)=\Omega (x^{1/4})$
, we cannot, at least by a direct argument, prevent a conspiracy among the large values of
$(\Delta (x/n))_n$
that would yield a cancellation among a linear combination of them.
To circumvent this, our approach is inspired by an elegant result of Tong [Reference Tong18]:
$$ \begin{align} \int_{1}^X\Delta(x)^2 dx=\frac{(1+o(1))}{6\pi^2}\sum_{n=1}^\infty \frac{\tau(n)^2}{n^{3/2}}\,X^{3/2}. \end{align} $$
By (1.2), the limit
$$ \begin{align*}\lim_{X\to\infty}\frac{1}{X^{3/2}}\int_{1}^X\left|\sum_{n\leq x}(f_1\ast f_2)(n)\right|^2dx\end{align*} $$
can be expressed as a quadratic form with matrix
$(c_{a,b})_{a,b|M_1M_2}$
, where
$c_{a,b}$
is the correlation
$$ \begin{align*} c_{a,b}:=\lim_{X\to\infty}\frac{1}{X^{3/2}}\int_{1}^X \Delta(x/a)\Delta(x/b)dx. \end{align*} $$
As it turns out, these correlations do not vanish and are computed in Theorem 1.6. With that in hand, the matrix correlation-term
$c_{a,b}$
can be expressed as
$$ \begin{align} \frac{C}{\sqrt{\gcd(a,b)}}\varphi\left(\frac{\operatorname{\mathrm{lcm}}(a,b)}{\gcd(a,b)}\right), \end{align} $$
for some constant
$C>0$
and multiplicative function
$\varphi $
.
This matrix entanglement is hard to analyze directly. In Section 5, we explore sufficient conditions for a matrix of the form (1.4) to be positive definite. When this happens, this ensures the referred
$\Omega $
-bound. Thanks to the Selberg diagonalization process, we show that when
$\varphi $
is completely multiplicative and satisfies other conditions, then this matrix is positive definite. The main proof somehow reduces to this case; we indeed find a way to conjugate our original matrix to reach a matrix related to a completely multiplicative function. With standard linear algebra of Hermitian matrices, we conclude that our matrix
$(c_{a,b})_{a,b|M_1M_2}$
is positive definite. We ended up with the following result.
Theorem 1.7 Let
$f_1$
and
$f_2$
be two periodic multiplicative functions satisfying i-ii-iii above with periods
$M_1$
and
$M_2$
, respectively. Let
$g=f_1\ast f_2\ast \mu \ast \mu $
and
$\gamma (n)$
the multiplicative function defined by
$$ \begin{align*}\gamma(n)=\prod_{p^{k}\| n } \frac{1-\tfrac{(k-1)}{(k+1)} p^{-3/2} }{1+ p^{-3/2}}.\end{align*} $$
Then the following limit
$$ \begin{align*}\lim_{X\to\infty}\frac{1}{X^{3/2}}\int_1^X\left|\sum_{n\leq x}(f_1\ast f_2)(n) \right|^2 dx\end{align*} $$
is positive and equals to
$$ \begin{align*}\frac{\zeta(3/2)^4}{\zeta(3)}\sum_{n,m|M_1M_2}g(n)\overline{g(m)}\frac{\gcd(n,m)^{3/2}}{nm}\tau\left(\frac{nm}{\gcd(n,m)^2}\right)\gamma\left(\frac{nm}{\gcd(n,m)^2}\right).\end{align*} $$
1.3 Byproduct study
Motivated by Nyman’s reformulation of the Riemann hypothesis [Reference Nyman15], in recent papers [Reference Báez-Duarte, Balazard, Landreau and Saias2, Reference Balazard and Martin3, Reference Balazard and Martin4] by Balazard, Duarte, and Martin, the correlation
$$ \begin{align*} A(\theta):=\int_0^\infty\{x\}\{\theta x\}\frac{dx}{x^2} \end{align*} $$
has been thoroughly studied. Here,
$\theta>0$
is any real number and
$\{x\}$
stands for the fractional part of x. Several analytic properties for the function
$A(\theta )$
have been shown.
Motivated by this, we studied the “divisor” analogue
$$ \begin{align*}I(\theta)=\lim_{X\to\infty}\frac{1}{X^{3/2}}\int_{1}^X \Delta(x)\Delta(\theta x)dx.\end{align*} $$
As stated in Theorem 1.6, when
$\theta =p/q$
is a rational number, the limit above is described by a positive multiplicative function depending on p and q. However, and somewhat surprisingly, when
$\theta $
is irrational, this correlation vanishes. The next proposition establishes that this vanishing is indeed very strong, except maybe at points
$\theta $
that are well approximated by rationals.
Proposition 1.8 Let
$\theta>0$
be an irrational number with irrationality measure
$\eta +1$
; that is, for each
$\epsilon>0$
, there is a constant
$C>0$
such that the inequality
$$ \begin{align*}|n-m\theta|\geq \frac{C}{m^{\eta+\epsilon}}\end{align*} $$
is violated only for a finite number of positive integers n and m. Then, for every positive
$\epsilon $
, we have
$$ \begin{align*}\int_{1}^X\Delta(x)\Delta(\theta x)dx=O(X^{3/2-1/(18\eta)+\epsilon}).\end{align*} $$
In the other cases of irrationals
$\theta $
, the integral above is
$o(X^{3/2})$
.
This shows that we have decorrelation among the values
$\Delta (x)$
and
$\Delta (\theta x)$
when
$\theta $
is irrational, and moreover, this gives that the function
$I(\theta )$
is continuous at the irrational numbers and discontinuous at the rationals. Another interesting remark is a result due to Khintchine [Reference Khintchine11] that states that almost all irrational numbers, with respect to (w.r.t.) Lebesgue measure, have irrationality measure equals to
$2$
.
Therefore, this result of Khintchine allow us to state the following Corollary from Proposition 1.8.
Corollary 1.9 For almost all irrational numbers
$\theta $
w.r.t. Lebesgue measure, for all small fixed
$\epsilon>0$
,
$$ \begin{align*}\int_{1}^X\Delta(x)\Delta(\theta x)dx=O(X^{3/2-1/18+\epsilon}).\end{align*} $$
We mention that a similar decorrelation also has been obtained by Ivić and Zhai in [Reference Ivić and Zhai10]. In this paper, they show decorrelation between
$\Delta (x)$
and
$\Delta _k(x)$
, where
$\Delta _k(x)$
is the error term related to the k-fold divisor function, and
$k=3$
or
$4$
.
2 Notation
2.1 Asymptotic notation
We employ both Vinogradov’s notation
$f\ll g$
or
$f=O(g)$
whenever there exists a constant
$C>0$
such that
$|f(x)|\leq C|g(x)|$
, for all x in a set of parameters. When not specified, this set of parameters is
$x\in (a,\infty )$
for sufficiently large
$a>0$
. We employ
$f=o(g)$
when
$\lim _{x\to a} \frac {f(x)}{g(x)}=0$
. In this case, a can be a complex number or
$\pm \infty $
. Finally,
$f=\Omega (g)$
when
$\limsup _{x\to a}\frac {|f(x)|}{g(x)}>0$
, where a is as in the previous notation.
2.2 Number-theoretic notation
Here, p stands for a generic prime number. We sometimes denote the least common multiple between
$a,b$
as
$\operatorname {\mathrm {lcm}}(a,b)$
. The greatest common divisor is denoted by
$\gcd (a,b)$
. The symbol
$\ast $
stands for Dirichlet convolution between two arithmetic functions:
$(f\ast g)(n)=\sum _{d|n}f(d)g(n/d)$
.
3 Multiplicative auxiliaries
Our first task is to evaluate
$ \sum _{n\ge 1}{\tau (cn)\tau (dn)}/{n^{3/2}} $
for coprime positive integers c and d.
Lemma 3.1 Let c be fixed positive number and
$f(n)$
be a multiplicative function with
$f(c)\neq 0$
. Then
$n\mapsto \frac {f(cn)}{f(c)}$
is multiplicative.
Proof For positive integers
$u,v$
, we have
$$ \begin{align*} f(u)f(v)=f(\gcd(u,v))f(\operatorname{\mathrm{lcm}}(u,v)). \end{align*} $$
Let
$u=cn$
,
$v=cm$
with
$\gcd (n,m)=1$
. Then
$f(cn)f(cm)=f(c)f(cnm)$
. Therefore, we obtain
$$ \begin{align*} \frac{f(cm)}{f(c)}\frac{f(cn)}{f(c)}=\frac{f(cnm)}{f(c)}.\\[-44pt] \end{align*} $$
Lemma 3.2 Let
$c,d$
be two fixed positive integers with
$\gcd (c,d)=1$
. Then
$$ \begin{align*} \sum_{n= 1}^\infty \frac{\tau(cn)\tau(dn)}{n^{s}} =\tau(cd)\frac{\zeta(s)^4}{\zeta(2s)} \prod_{p^{k}\| cd } \left(1+ p^{-s}\right)^{-1} \left(1-\tfrac{(k-1)}{(k+1)} p^{-s}\right). \end{align*} $$
The quantity we compute appears in several places – for instance, in [Reference Lee and Lee14] by Lee and Lee and in [Reference Borda, Munsch and Shparlinski5] by Borda, Munsch, and Shparlinski.
Proof Note that
$\frac {\tau (cn)}{\tau (c)}$
is a multiplicative function in the variable n by Lemma 3.1, and so is
$\frac {\tau (cn)\tau (dn)}{\tau (c)\tau (d)}$
. Therefore, for
$\Re (s)>1$
, we have the following Euler factorization:
$$ \begin{align*} \sum_{n= 1}^\infty \frac{\tau(cn)\tau(dn)} {\tau(c)\tau(d)n^{s}} = \prod_{p\nmid cd } \left(1 + \sum_{\ell= 1}^\infty \frac{\tau(p^\ell)^{2}}{p^{\ell s}} \right) \prod_{p\mid cd } \left(1 + \sum_{\ell= 1}^\infty \frac{\tau(cp^\ell)\tau(dp^\ell)}{\tau(c) \tau(d) p^{\ell s}} \right). \end{align*} $$
For
$|x|<1$
, we know that
$$ \begin{align*} \sum_{\ell= 0}^\infty(\ell+1)x^{\ell} = \frac{1}{(1-x)^{2}}, \;\;\quad\quad \sum_{\ell=0}^\infty(\ell+1)^{2}x^{\ell} = \frac{(1+x)}{(1-x)^{3}}, \end{align*} $$
from which we also derive that
$$ \begin{align*} \sum_{\ell=0}^\infty\ell(\ell+1) x^{\ell}= \frac{2x}{(1-x)^{3}}. \end{align*} $$
Now,
$$ \begin{align*} \prod_{p\nmid cd } \left(1 + \sum_{\ell= 1}^\infty\frac{\tau(p^\ell)^{2}}{p^{\ell s}} \right) &= \prod_{p } \left(1 + \sum_{\ell= 1}^\infty\frac{(\ell+1)^{2}}{p^{\ell s}} \right) \prod_{p\mid cd } \left(1 + \sum_{\ell= 1}^\infty\frac{(\ell+1)^{2}}{p^{\ell s}} \right)^{-1}\\ &=\prod_{p } \frac{\left(1+ p^{-s}\right)}{\left(1- p^{-s}\right)^{3}}\prod_{p| cd } \frac{\left(1- p^{-s}\right)^{3}}{\left(1+ p^{-s}\right)}\\ &=\frac{\zeta(s)^4}{\zeta(2s)} \prod_{p| cd } \frac{\left(1- p^{-s}\right)^{3}}{\left(1+ p^{-s}\right)}. \end{align*} $$
If
$\gcd (c,d)=1$
,
$$ \begin{align*} \prod_{p\mid cd } \left(1 + \sum_{\ell= 1}^\infty \frac{\tau(cp^\ell)\tau(dp^\ell)}{\tau(c) \tau(d) p^{\ell s}} \right) &=\prod_{p^{k}\| cd } \left(1 + \sum_{\ell= 1}^\infty\frac{(k+1+\ell)(\ell+1)}{(k+1)p^{\ell s}} \right) \\ &=\prod_{p^{k}\| cd } \left( 1+ \sum_{\ell= 1}^\infty\frac{(\ell+1)}{p^{\ell s}} +\frac{1}{k+1}\sum_{\ell= 1}^\infty\frac{\ell(\ell+1)}{p^{\ell s}} \right)\\ &=\prod_{p^{k}\| cd } \left(1- p^{-s}\right)^{-3}\left(1-\tfrac{(k-1)}{(k+1)} p^{-s}\right).\\[-47pt] \end{align*} $$
4 Correlations of the
$\Delta $
function
We continue with the proof with the following Lemma.
Lemma 4.1 Let
$a>0$
. Then
$$ \begin{align*}\int x^2\cos(ax)dx=x^2\frac{\sin(ax)}{a}+2x\frac{\cos(ax)}{a^2}-2\frac{\sin(ax)}{a^3}.\end{align*} $$
Moreover, for any
$X>1$
,
$$ \begin{align*}\int_{1}^Xx^2\cos(ax)dx\ll \frac{X^2}{a},\;\int_{1}^Xx^2\sin(ax)dx\ll \frac{X^2}{a}.\end{align*} $$
Proof We do integration by parts:
$$ \begin{align*}\int x^2\cos(ax)dx=x^2\frac{\sin(ax)}{a}-\int \frac{2x\sin(ax)}{a}dx.\end{align*} $$
By making the trivial bound
$|\sin (ax)|\leq 1$
in the right-hand side of the equation above, we reach to the second claim of the proposed Lemma. By making integration by parts, the last integral of the equation above gives the first claim of the Lemma. Similar arguments give similar results for
$\sin $
in place of
$\cos $
.
Lemma 4.2 Let
$a,b$
be positive integers,
$\lambda =\gcd (a,b)$
,
$c=a/\lambda $
and
$d=b/\lambda $
. Then
$$ \begin{align*} \lim_{X\to\infty}\frac{1}{X^{3/2}}\int_1^X\Delta(x/a)\Delta(x/b)dx = \frac{1}{6\pi^2\sqrt{\lambda}cd} \sum_{n=1}^\infty\frac{\tau(cn)\tau(dn)}{n^{3/2}}. \end{align*} $$
Proof Let
$N>0$
and
$\epsilon>0$
be a small number that may change from line after line. We proceed with Voronoï’s formula for
$\Delta (x)$
in the following form (see [Reference Lau and Tsang13]):
$$ \begin{align*} \Delta(x)=\frac{x^{1/4}}{\pi\sqrt{2}}\sum_{n\leq N}\frac{\tau(n)}{n^{3/4}}\cos(4\pi\sqrt{nx}-\pi/4)+R_N(x), \end{align*} $$
where, for every positive
$\epsilon $
, we have
$$ \begin{align*} R_N(x)\ll x^\epsilon+\frac{x^{1/2+\epsilon}}{N^{1/2}}. \end{align*} $$
We select N at the end. With this formula, we have that in the range
$1\leq x\leq X$
,
$$ \begin{align*} \Delta(x/a) &=\frac{(x/a)^{1/4}}{\pi\sqrt{2}} \sum_{n\leq N}\frac{\tau(n)}{n^{3/4}}\cos(4\pi\sqrt{nx/a}-\pi/4) +R_N(x/a)\\&=U_N(x/a)+R_N(x/a) \end{align*} $$
say.
Now,
$$ \begin{align*} \int_{1}^X\Delta(x/a)\Delta(x/b)dx&=\int_{1}^X U_N(x/a)U_N(x/b)dx \\& \quad +\int_{1}^X U_N(x/a)R_N(x/b)dx\\& \quad +\int_{1}^X U_N(x/b)R_N(x/a)dx\\&\quad +\int_{1}^X R_N(x/a)R_N(x/b)dx\\& =\int_{1}^X U_N(x/a)U_N(x/b)dx\\&\quad+O\left(X^{1+1/4+\epsilon}+\frac{X^{1+3/4+\epsilon}}{\sqrt{N}} +\frac{X^{2+\epsilon}}{N} \right), \end{align*} $$
where we used the Cauchy-Schwarz inequality and (1.3) in the last equality. By making the change of variable
$u=x/\lambda $
, we reach
$$ \begin{align*} &\int_{1}^X U_N(x/a)U_N(x/b)dx=\lambda\int_{1}^{X/\lambda} U_N(x/c)U_N(x/d)dx\\& \quad =\frac{\lambda}{2\pi^2(cd)^{1/4}}\sum_{n,m\leq N}\frac{\tau(n)\tau(m)}{(nm)^{3/4}}\cdot\\& \qquad \cdot\int_{1}^{X/\lambda} x^{1/2}\cos(4\pi\sqrt{nx/c}-\pi/4)\cos(4\pi\sqrt{mx/d}-\pi/4)dx \\& \quad =\frac{\lambda}{\pi^2(cd)^{1/4}} \sum_{n,m\leq N} \frac{\tau(n)\tau(m)}{(nm)^{3/4}}\cdot\\& \qquad \cdot\int_{1}^{(X/\lambda)^{1/2}} u^2 \cos(4\pi u\sqrt{n/c}-\pi/4)\cos(4\pi u\sqrt{m/d}-\pi/4)du, \end{align*} $$
where in the last equality above we made a change of variable
$u=\sqrt {x}$
. We claim now that the main contribution comes when
$n/c=m/d$
. Since c and d are coprime, this implies that
$m=dk$
and
$n=ck$
. Therefore, the sum over these n and m can be written as
$$ \begin{align} \frac{\lambda}{\pi^2cd} \sum_{k=1}^\infty \frac{\tau(ck)\tau(dk)}{k^{3/2}} \int_{1}^{(X/\lambda)^{1/2}} u^2\cos^2(4\pi u\sqrt{k}-\pi/4) du+O\left(\frac{X^{3/2+\epsilon}}{\sqrt{N}}\right). \end{align} $$
We recall now that
$\cos ^2(v)=\frac {1+\cos (2v)}{2}$
; hence, by Lemma 4.1, the integral above is
$$ \begin{align} \int_{1}^{X^{1/2}/\lambda^{1/2}} x^2\cos^2(4\pi\sqrt{n}x-\pi/4)dx=\frac{X^{3/2}}{6\lambda^{3/2}}+O(X), \end{align} $$
where the big-oh term is uniform in n. Now we will show that the sum over those n and m such that
$n/c\neq m/d$
will be
$o(X^{3/2})$
. With this, the proof is complete by combining (4.1) and (4.2).
We recall the identity
$2\cos (u)\cos (v)=\cos (u-v)+\cos (u+v)$
. Thus, for
$\sqrt {n/c}\neq \sqrt {m/d}$
, by Lemma 4.1, we find that
$$ \begin{align*} &\int_{1}^{X^{1/2}/\lambda^{1/2}} x^2\cos(4\pi\sqrt{n/c}x-\pi/4)\cos(4\pi\sqrt{m/d}x-\pi/4)dx\\& \quad =\frac{1}{2}\int_{1}^{X^{1/2}/\lambda^{1/2}} x^2\cos(4\pi(\sqrt{n/c}-\sqrt{m/d})x)dx\\& \qquad +\frac{1}{2}\int_{1}^{X^{1/2}/\lambda^{1/2}} x^2\sin(4\pi(\sqrt{n/c}+\sqrt{m/d})x)dx\\& \quad \ll \frac{X}{\left|\sqrt{n/c}-\sqrt{m/d}\right|} + \frac{X}{\sqrt{n/c}+\sqrt{m/d}} \\& \quad \ll\frac{\sqrt{n/c}+\sqrt{m/d}}{|nd-mc|}X. \end{align*} $$
Let 
be the indicator that n has property P. We find that
On calling this sum S, we readily continue with
$$ \begin{align*} S&\ll X N^\epsilon \sum_{k=1}^{N\max(c,d)}\frac{1}{k}\sum_{m\leq N}\frac{\sqrt{m}+\sqrt{k}}{((k+mc)m)^{3/4}}\\ &\ll X N^\epsilon\left(O(\log N)^2+\sum_{k\leq N}\frac{1}{\sqrt{k}}\sum_{m\leq N}\frac{1}{(m^2+mk)^{3/4}} \right)\\ &\ll X N^\epsilon\left(O(\log N)^2+\sum_{k\leq N}\frac{1}{\sqrt{k}}\left(\sum_{k\leq m\leq N}\frac{1}{m^{3/2}}+\frac{1}{k^{3/4}}\sum_{m\leq k}\frac{1}{m^{3/4}}\right) \right)\\ &\ll X N^\epsilon (\log N)^2. \end{align*} $$
Finally, by selecting
$N=X^2$
, we arrive at
$$ \begin{align*} \int_1^X\Delta(x/a)\Delta(x/b)dx = \frac{1}{6\pi^2\sqrt{\lambda}cd}\left( \sum_{n=1}^\infty\frac{\tau(cn)\tau(dn)}{n^{3/2}}\right)X^{3/2}+O(X^{3/2-1/4+\epsilon}), \end{align*} $$
where the main contribution in the O-term above comes from the usage of Cauchy-Schwarz in the beginning of the proof.
The proof is complete.
Now we deviate from the main line and prove Proposition 1.8.
Proof of Proposition 1.8
By the proof of Lemma 4.2 we have that
$$ \begin{align*} I_\theta(X):=&\int_{1}^X\Delta(x)\Delta(\theta x)dx\\=&\frac{1}{\pi^2} \sum_{n,m\leq N} \frac{\tau(n)\tau(m)}{(nm)^{3/4}} \int_{1}^{X^{1/2}} x^2 \cos(4\pi x\sqrt{n}-\pi/4)\cos(4\pi x\sqrt{m\theta}-\pi/4)dx\\&+O\left(X^{1+1/4+\epsilon}+\frac{X^{1+3/4+\epsilon}}{\sqrt{N}}+\frac{X^{2+\epsilon}}{N}\right). \end{align*} $$
Now, by appealing to the identity
$2\cos (u)\cos (v)=\cos (u-v)+\cos (u+v)$
, we reach at
$$ \begin{align*} I_\theta(X)&=\frac{1}{2\pi^2} \sum_{n,m\leq N} \frac{\tau(n)\tau(m)}{(nm)^{3/4}} \int_{1}^{X^{1/2}} x^2 \cos(4\pi x(\sqrt{n}-\sqrt{m\theta}))dx \\&\quad +\frac{1}{2\pi^2} \sum_{n,m\leq N} \frac{\tau(n)\tau(m)}{(nm)^{3/4}} \int_{1}^{X^{1/2}} x^2 \sin(4\pi x(\sqrt{n}+\sqrt{m\theta}))dx\\&\quad +O\left(X^{1+1/4}+\frac{X^{1+3/4+\epsilon}}{\sqrt{N}} +\frac{X^{2+\epsilon}}{N}\right). \end{align*} $$
We have that, by Lemma 4.1,
$$ \begin{align*} \sum_{n,m\leq N}& \frac{\tau(n)\tau(m)}{(nm)^{3/4}} \int_{1}^{X^{1/2}} x^2 \sin(4\pi x(\sqrt{n}+\sqrt{m\theta}))dx \\& \ll X N^\epsilon \sum_{n,m\leq N}\frac{1}{m^{3/4}n^{5/4}+n^{3/4}m^{5/4}}\\&\ll X N^\epsilon \sum_{n,m\leq N}\frac{1}{n^{3/4}m^{5/4}}\\& \ll X N^{1/4+\epsilon}. \end{align*} $$
Thus, we reach at
$$ \begin{align*} I_\theta(X)&=\frac{1}{2\pi^2} \sum_{n,m\leq N} \frac{\tau(n)\tau(m)}{(nm)^{3/4}} \int_{1}^{X^{1/2}} x^2 \cos(4\pi x(\sqrt{n}-\sqrt{m\theta}))dx\\& \quad +O\left(X^{1+1/4}+\frac{X^{1+3/4+\epsilon}}{\sqrt{N}} +\frac{X^{2+\epsilon}}{N}+XN^{1/4+\epsilon}\right). \end{align*} $$
On calling the last sum above
$S_\theta (X)$
,
$a_{n,m}:=4\pi (\sqrt {n} - \sqrt {m\theta })$
, we obtain that
$$ \begin{align*}S_\theta(X)=X^{3/2}\sum_{n,m\leq N} \frac{\tau(n)\tau(m)}{(nm)^{3/4}}\Lambda(a_{n,m}\sqrt{X}),\end{align*} $$
where, by Lemma 4.1,
$\Lambda (0):=1/3$
and for
$u\neq 0$
,
$$ \begin{align*}\Lambda(u):=\frac{\sin(u)}{u}+2\frac{\cos(u)}{u^2}-2\frac{\sin(u)}{u^3}.\end{align*} $$
A careful inspection shows that
$\Lambda $
is continuous and for large
$|u|$
,
$\Lambda (u)\ll |u|^{-1}$
.
Now, for a large parameter T (to be chosen), we split
$$ \begin{align*} S_\theta(X)&=X^{3/2}\sum_{\substack{n,m\leq N\\ |a_{n,m}\sqrt{X}|\leq T}} \frac{\tau(n)\tau(m)}{(nm)^{3/4}}\Lambda(a_{n,m}\sqrt{X})\\&\quad+X^{3/2}\sum_{\substack{n,m\leq N\\ |a_{n,m}\sqrt{X}|> T}} \frac{\tau(n)\tau(m)}{(nm)^{3/4}}\Lambda(a_{n,m}\sqrt{X}). \end{align*} $$
We call the first sum in the right-hand side above diagonal contribution and the second sum the nondiagonal contribution. We select
$T=X^{1/2-\delta }$
and
$N=X^{1/2+\delta }$
, for some small
$\delta>0$
.
The diagonal contribution. We have that
$$ \begin{align} D(X)&=X^{3/2}\sum_{\substack{n,m\leq N\\ |a_{n,m}\sqrt{X}|\leq T}} \frac{\tau(n)\tau(m)}{(nm)^{3/4}}\Lambda(a_{n,m}\sqrt{X}) \end{align} $$
$$ \begin{align} &\ll X^{3/2}N^\epsilon\sum_{m\leq N}\frac{1}{m^{3/4}}\sum_{\substack{n;\\|n-m\theta|\leq\frac{2\sqrt{m\theta}}{X^\delta}+\frac{1}{X^{2\delta}}}}\frac{|\Lambda(a_{n,m}\sqrt{X})|}{n^{3/4}}. \end{align} $$
The inner sum above we split accordingly
$\frac {2\sqrt {m\theta }}{X^\delta }+\frac {1}{X^{2\delta }}$
is below and above
$1$
. In the case that this quantity is greater or equal to
$1$
, we have that
$m\geq (4\theta )^{-1}X^{2\delta }$
, and hence,
$$ \begin{align*} D(X)&\ll X^{3/2}N^\epsilon\sum_{(4\theta)^{-1}X^{2\delta}\leq m\leq N}\frac{1}{m^{3/4}}\sum_{\substack{n;\\|n-m\theta|\leq\frac{2\sqrt{m\theta}}{X^\delta}+\frac{1}{X^{2\delta}}}}\frac{|\Lambda(a_{n,m}\sqrt{X})|}{n^{3/4}}\\&\ll X^{3/2}N^\epsilon\sum_{ (4\theta)^{-1}X^{2\delta}\leq m\leq N}\frac{1}{m^{3/4}}\cdot \frac{1}{m^{3/4}}\frac{\sqrt{m}}{X^\delta}\\&\ll X^{3/2-\delta}N^{\epsilon}. \end{align*} $$
In the case that
$\frac {2\sqrt {m\theta }}{X^\delta }+\frac {1}{X^{2\delta }}\leq 1$
, we have that
$m\leq (4\theta )^{-1}X^{2\delta }$
, and now the Diophantine properties of
$\theta $
come into play. If the irrationality measure of
$\theta $
is
$\eta +1$
, we have that for each
$\epsilon $
, there is a constant
$C>0$
such that the inequality
$$ \begin{align*}|n-m\theta|\geq \frac{C}{m^{\eta+\epsilon}}\end{align*} $$
is violated only for a finite number of positive integers n and m. In our case, this allows us to lower bound
$|a_{n,m}\sqrt {X}|$
for all but a finite number of n and m such that
$1\leq m\ll X^{2\delta }$
and
$1/2\le \sqrt {n}/\sqrt {m\theta }\le 2$
:
$$ \begin{align*} |a_{n,m}\sqrt{X}|\cdot\frac{\sqrt{n}+\sqrt{m\theta}}{\sqrt{n}+\sqrt{m\theta}}&=\sqrt{X}\frac{|n-m\theta|}{\sqrt{n}+\sqrt{m\theta}}\\ &\geq \frac{\sqrt{X}}{m^{\eta+\epsilon}(\sqrt{n}+\sqrt{m\theta})}\\ &\gg X^{1/2-(2\eta+1)\delta-\epsilon}. \end{align*} $$
Observe that the diagonal contribution from those exceptional n and m will be at most
$O(X)$
. With these estimates on hand and recalling that
$\Lambda (u)\ll |u|^{-1}$
, we obtain
$$ \begin{align*} &X^{3/2}N^\epsilon\sum_{m\leq (4\theta)^{-1}X^{2\delta}}\frac{1}{m^{3/4}}\sum_{\substack{n;\\|n-m\theta|\leq\frac{2\sqrt{m\theta}}{X^\delta}+\frac{1}{X^{2\delta}}}}\frac{|\Lambda(a_{n,m}\sqrt{X})|}{n^{3/4}}\\& \quad \ll X^{3/2}N^\epsilon\sum_{m\leq(4\theta)^{-1}X^{2\delta}}\frac{1}{m^{3/2}}\cdot \frac{1}{X^{1/2-(2\eta+1)\delta-\epsilon}}+O(X)\\& \quad \ll X^{1+(2\eta+1)\delta+\epsilon}. \end{align*} $$
Therefore, the diagonal contribution is at most
$$ \begin{align*}D(X)\ll X^{1+(2\eta+1)\delta+\epsilon} +X^{3/2-\delta+\epsilon}.\end{align*} $$
The nondiagonal contribution. Now, we reach
$$ \begin{align*} X^{3/2}\sum_{\substack{n,m\leq N\\ |a_{n,m}\sqrt{X}|> T}} \frac{\tau(n)\tau(m)}{(nm)^{3/4}}\Lambda(a_{n,m}\sqrt{X})&\ll \frac{X^{3/2}N^{1/2+\epsilon}}{T}\\ &=X^{3/2+1/4+(\delta+\epsilon)/2+\epsilon\delta-1/2+\delta}\\ &=X^{1+1/4+3\delta/2+\epsilon/2+\epsilon\delta}. \end{align*} $$
We choose
$\delta =\frac {1}{3(2\eta +1)}$
and obtain
$$ \begin{align*}I_\theta(X)=O(X^{3/2-1/(18\eta)}).\end{align*} $$
The proof of the first part of Proposition 1.8 is complete.
Now we assume that
$\theta $
is a Liouville number (i.e.,
$\theta $
does not have finite irrationality measure). We see that the nondiagonal argument does not depend on the Diophantine properties of
$\theta $
. Let
$\eta>0$
be a large fixed number,
$t>0$
a small number that will tend to
$0$
. For
$D(X)$
as in (4.3), by repeating verbatim the estimates above, we have that
$$ \begin{align*} D(X)&\ll X^{3/2}\sum_{m\leq(4\theta)^{-1}X^{2\delta}}\frac{\tau(m)}{m^{3/4}}\sum_{\substack{n;\\|n-m\theta|\leq\frac{2\sqrt{m\theta}}{X^\delta}+\frac{1}{X^{2\delta}}}}\frac{\tau(n)|\Lambda(a_{n,m}\sqrt{X})|}{n^{3/4}}\\&\quad+O(X^{3/2-\delta}N^{\epsilon}). \end{align*} $$
Let
$\|x\|$
be the distance from x to the nearest integer. We split the sum over m above into two sums: One over those m such that
$\|m\theta \|> t m^{-\eta }$
and the other over m such that
$\|m\theta \|\leq t m^{-\eta }$
.
Repeating the argument above for non-Liouville numbers, we have that the contribution over those m such that
$\|m\theta \|> t m^{-\eta }$
is
$O(t^{-1}X^{1+\delta (2\eta +1)})$
. Therefore,
$$ \begin{align*}D(X)\ll X^{3/2}\sum_{\substack{m=1\\{\|m\theta\|\leq tm^{-\eta}}}}^\infty\frac{1}{m^{3/2-\epsilon}}+O(t^{-1}X^{1+\delta(2\eta+1)}+X^{3/2-\delta+\epsilon}).\end{align*} $$
Combining all these estimates, we see that
$$ \begin{align*}\limsup_{X\to\infty}\frac{1}{X^{3/2}}\left|\int_{1}^X\Delta(x)\Delta(\theta x)dx\right| \ll \sum_{\substack{m=1\\{\|m\theta\|\leq tm^{-\eta}}}}^\infty\frac{1}{m^{3/2-\epsilon}}.\end{align*} $$
Since the upper bound above holds for all
$t>0$
, we have that as
$t\to 0^+$
, the sum above converges to
$0$
and thus implies that the
$\limsup $
is
$0$
. The proof is complete.
5 Quadratic forms auxiliaries
The main proof will lead to considering the quadratic form attached to a matrix of the form
$$ \begin{align} M_{S, \varphi}=\bigg(\frac{1}{\sqrt{\gcd(a,b)}} \varphi\bigg(\frac{\operatorname{\mathrm{lcm}}(a,b)}{\gcd(a,b)}\bigg) \bigg)_{a,b\in S}, \end{align} $$
where S is some finite set of integers, while
$\varphi $
is a nonnegative multiplicative function such that
$\varphi (p^k)\le 1$
. So we stray somewhat from the main line and investigate this situation. Our initial aim is to find conditions under which the associated quadratic form is positive definite, but we shall finally restrict our scope. GCD-matrices have received quite some attention, but it seems the matrices occuring in (5.1) have not been explored. We obtain results in two specific contexts.
Completely multiplicative case
Here is our first result.
Lemma 5.1 When
$\varphi $
is completely multiplicative and
$p^{1/4}\varphi (p)\in (0,1]$
, the matrix
$M_{S, \varphi }$
is nonnegative. When in addition we assume that
$p^{1/4}\varphi (p)\in (0,1)$
and S is divisor closed, this matrix is positive definite. The determinant in that case is given by the formula
$$ \begin{align*} \det \bigg(\frac{1}{\sqrt{\gcd(a,b)}} \varphi\bigg(\frac{\operatorname{\mathrm{lcm}}(a,b)}{\gcd(a,b)}\bigg) \bigg)_{a,b\in S} =\prod_{d\in S}\varphi(d)^2(\mu\ast \psi)(d), \end{align*} $$
where
$\psi $
is the completely multiplicative function given by
$\psi (p)=1/(\sqrt {p}\varphi (p)^2)$
.
By divisor closed, we mean that every divisor of an element of S also belongs to S.
Proof We write
$$ \begin{align*} \frac{1}{\sqrt{\gcd(a,b)}} \varphi\bigg(\frac{\operatorname{\mathrm{lcm}}(a,b)}{\gcd(a,b)}\bigg) =\varphi(a)\varphi(b)\psi(\gcd(a,b)), \end{align*} $$
where
$\psi (n)=1/(\varphi (n)^2\sqrt {n})$
is another nonnegative multiplicative function. We introduce the auxiliary function
$h=\mu \ast \psi $
. Notice that this function is multiplicative and nonnegative, as
$\psi (p)\ge 1$
. We use Selberg’s diagonalization process to write
$$ \begin{align*} \sum_{a,b\in S} \frac{1}{\sqrt{\gcd(a,b)}} \varphi\bigg(\frac{\operatorname{\mathrm{lcm}}(a,b)}{\gcd(a,b)}\bigg)x_ax_b &= \sum_{a,b\in S} \psi(\gcd(a,b)) \varphi(a)x_a\varphi(b)x_b \\& =\sum_{a,b\in S} \sum_{d|\gcd(a,b)}h(d)\varphi(a)x_a\varphi(b)x_b\\ &= \sum_{d} h(d)\bigg(\sum_{\substack{a\in S\\ d|a}}\varphi(a)x_a\bigg)^2 \end{align*} $$
from which the nonnegativity follows readily. When
$\varphi $
verifies the more stringent condition that
$p^{1/4}\varphi (p)\in (0,1)$
, we know that both
$\varphi $
and h are strictly positive. Let us define
$y_d=\sum _{\substack {a\in S\\ d|a}}\varphi (a)x_a$
. The variable d varies in the set D of divisors of S. We assume that S is divisor closed, so that
$D=S$
. We can readily invert the triangular system giving the
$y_d$
’s as functions of the
$x_a$
’s into
$$ \begin{align*} \varphi(a)x_a=\sum_{a|b}\mu(b/a)y_b. \end{align*} $$
Indeed, the fact that the mentioned system is triangular ensures that a solution y is unique if it exists. We next verify that the proposed expression is indeed a solution by
$$ \begin{align*} \sum_{\substack{a\in S\\ d|a}}\varphi(a)x_a =\sum_{\substack{a\in S\\ d|a}}\sum_{a|b}\mu(b/a)y_b =\sum_{\substack{b\in S\\ d|b}}y_b\sum_{d|a|b}\mu(b/a)=y_d \end{align*} $$
as the last inner sum vanishes when
$d\neq b$
. We thus have a writing as a linear combination of squares of independant linear forms. In a more pedestrian manner, if our quadratic form vanishes, then all
$y_d$
’s do vanish, and hence, so do the
$x_a$
’s.
Here is a corollary.
Lemma 5.2 When the set S contains solely squarefree integers, the matrix
$M_{S,\varphi }$
is nonnegative.
Proof Simply apply Lemma 5.1 to the completely multiplicative function
$\varphi '$
that has the same values on primes as
$\varphi $
.
Now we recall the Sylvester’s criterion.
Lemma 5.3 A hermitian complex valued matrix
$M=(m_{i,j})_{i,j\le K}$
defines a positive definite form if and only if all its principal minors
$ \det (m_{i,j})_{i,j\le k} $
for
$k\le K$
are positive.
A tensor product-like situation
Lemma 5.2 is enough to solve our main problem when
$M_1$
and
$M_2$
are coprime squarefree integers. We need to go somewhat further. Let S be a divisor closed set. We consider the quadratic form
$$ \begin{align} \sum_{a,b\in S}\varphi\bigg(\frac{\operatorname{\mathrm{lcm}}(a,b)}{\gcd(a,b)}\bigg)x_a x_b, \end{align} $$
where the variables
$x_a$
’s are also multiplicatively split; that is,
$$ \begin{align} x_a=\prod_{p^k\|a}x_{p^k}. \end{align} $$
Let
$S(p)$
the subset of S made only of
$1$
and of prime powers. We extend S so that it contains every products of integers from any collection of distinct
$S(p)$
.Footnote
1
We then find that
$$ \begin{align} \sum_{a,b\in S}\frac{1}{\sqrt{\gcd(a,b)}} \varphi\bigg(\frac{\operatorname{\mathrm{lcm}}(a,b)}{\gcd(a,b)}\bigg)x_a x_b =\prod_{p\in S}\bigg( \sum_{p^{k},p^\ell\in S(p)} \frac{\varphi\big(p^{\max(k,\ell)-\min(k,\ell)}\big)}{p^{\min(k,\ell)/2}} x_{p^k} x_{p^\ell} \bigg).\nonumber\\ \end{align} $$
We check this identity simply by opening the right-hand side and seeing that every summand from the left-hand side appears one and only one time.
6 Proof of the main result
Proof By [Reference Aymone1, Theorem 1.4], we have
$$ \begin{align*} S(x)=\sum_{n\le x}(f_1\ast f_2)(n) = \sum_{a| M_1M_2}g(a)\Delta(x/a), \end{align*} $$
where
$g=f_1\ast f_2\ast \mu \ast \mu $
. We infer from this formula that
$$ \begin{align*} &\int_1^X|S(x)|^2dx = \sum_{a,b| M_1M_2}g(a)g(b) \int_1^X \Delta(x/a)\Delta(x/b)dx \\& \quad = \frac{(1+o(1))}{6\pi^2}X^{3/2} \sum_{a,b|M_1M_2}g(a)g(b) \frac{\gcd(a,b)^{3/2}}{ab} \sum_{n= 1}^\infty \frac{\tau\left(\frac{an}{\gcd(a,b)}\right)\tau\left(\frac{bn}{\gcd(a,b)}\right)}{n^{3/2}} \end{align*} $$
by Lemma 4.2. We next use Lemma 3.2 to infer that
$$ \begin{align*} \lim_{X\to\infty} \frac{1}{X^{3/2}}\int_1^X|S(x)|^2dx = \frac{\zeta(3/2)^4}{6\pi^2\zeta(3)} \sum_{a,b| M_1M_2}g(a)g(b) \frac{1}{ \sqrt{\gcd(a,b)}} \varphi\bigg(\frac{\operatorname{\mathrm{lcm}}(a,b)}{\gcd(a,b)}\bigg), \end{align*} $$
where
$\varphi $
is multiplicative and at prime powers:
$$ \begin{align} \begin{aligned} \varphi(p^k) &= \frac{(k+1)}{p^{k}}\frac{1}{1+p^{-3/2}} \bigg(1-\frac{(k-1)}{(k+1)p^{3/2}}\bigg)\\ &= \frac{1}{p^{k} (1 + p^{-3/2})} \bigg( (k+1) - (k-1)p^{-3/2} \bigg) \\ &= \frac{1}{p^{k} (1 + p^{-3/2})} \bigg( k (1-p^{-3/2}) + (1 + p^{-3/2}) \bigg)\\ &=\frac{k \beta(p) + 1 }{p^{k}}, \end{aligned} \end{align} $$
where
$$ \begin{align*}\beta(p) = \frac{1-p^{-3/2}}{1 + p^{-3/2}}. \end{align*} $$
Now, we can write
$$ \begin{align*} \frac{1}{\sqrt{\gcd(a,b)}} \varphi\left( \frac{\operatorname{\mathrm{lcm}}(a,b)}{\gcd(a,b)} \right) = \frac{1}{(ab)^{1/4}} \left( \frac{\operatorname{\mathrm{lcm}}(a,b)}{\gcd(a,b)} \right)^{1/4} \varphi\left( \frac{\operatorname{\mathrm{lcm}}(a,b)}{\gcd(a,b)} \right). \end{align*} $$
Since the terms
$a^{-1/4}$
and
$b^{-1/4}$
can be absorbed into the variables
$g(a)$
and
$g(b)$
of the quadratic form, it is enough to consider the quantity
$$ \begin{align*}\varphi^*\left( \frac{\operatorname{\mathrm{lcm}}(a,b)}{\gcd(a,b)} \right), \quad \text{where} \ \, \varphi^*(n) = n^{1/4} \varphi(n). \end{align*} $$
We note that, at the prime power
$p^k$
, we have
$$ \begin{align} \varphi^*(p^k) = p^{k/4} \varphi(p^k) =\frac{k \beta(p) + 1 }{p^{3k/4}}. \end{align} $$
Due to (5.4) and the discussion before it, we now restrict to the prime power case; that is, we look to matrices of the form
$$ \begin{align*} \mathcal{M}_{K} = \big( \varphi^*(p^{|i-j|}) \big)_{i,j \leq K}. \end{align*} $$
As we are dealing with a given prime p, we shorten
$\beta (p)$
in
$\beta $
.
Since
$\varphi ^*$
is not completely multiplicative, it is not clear how to handle the matrix
$\mathcal {M}_K$
directly. So, our aim will be to transform this into another matrix which in some way associates with a completely multiplicative function. So, let us consider
$$ \begin{align*}\mathcal{A}_K = \mathcal{U}_K^{\top} \mathcal{M}_K \, \mathcal{U}_K, \end{align*} $$
where,
$$ \begin{align} \mathcal{U}_K(i,j) = \begin{cases} \frac{\mu(p^{|i-j|})}{p^{3(|i-j|)/4}}, & \text{when } i \geq j \, \text{ or } \, (i,j) = (K-1, K), \\0, & \text{otherwise.} \end{cases} \end{align} $$
Simply speaking,
$\mathcal {U}_K$
is
$1$
on the diagonal and
$-p^{-3/4}$
on all
$(i+1,i)$
as well as
$(K-1, K)$
. Also,
$$ \begin{align*}\det(\mathcal{U}_K) = 1 - p^{-3/2} .\end{align*} $$
We now calculate the entries of the matrix
$\mathcal {A}_K$
. We have the following:
Proposition 6.1 The matrix
$\mathcal {A}_K$
above is given by
$$ \begin{align*}\mathcal{A}_K(i,j) = \beta(1 - p^{-3/2}) \cdot \begin{cases} p^{-3|i-j|/4}, & \text{when } \, {1 \leq i, j \leq K-1} \text{ or } i=j=K, \\ 0, & \text{otherwise}. \end{cases}\\[-41pt] \end{align*} $$
We begin with the following lemma:
Lemma 6.2 We have
$$ \begin{align*}\varphi^*(p^m) - p^{-3/4} \varphi^*(p^{|m-1|}) = p^{-3m/4} \beta, \quad \text{for all } \, m \geq 0. \end{align*} $$
Proof First, assume
$m \geq 1$
. We have
$$ \begin{align*} \varphi^*(p^m) - p^{-3/4} \varphi^*(p^{m-1}) = \frac{ m\beta + 1}{p^{3m/4}} - p^{-3/4} \frac{(m-1)\beta + 1}{p^{3(m-1)/4}} = p^{-3m/4} \beta. \end{align*} $$
When
$m=0$
, we have
$$ \begin{align*} 1 - p^{-3/4} \varphi^*(p) = 1 - p^{-3/2}(\beta+1) = 1 - \frac{2p^{-3/2}}{1 + p^{-3/2}} = \beta.\\[-41pt] \end{align*} $$
Now, we shall proceed with the proof of the Proposition 6.1.
Proof of Proposition 6.1
Let us first assume that
$1 \leq i, j \leq K-1$
. We have
$$ \begin{align} \begin{aligned} \mathcal{A}_K(i,j) &= \sum\limits_{k_1, k_2} \mathcal{U}_K^{\top}(i, k_1) \mathcal{M}_K(k_1, k_2) \,\mathcal{U}_K(k_2, j)\\ &= \sum\limits_{\substack{k_1 - i \in \{0,1\} \\ k_2 - j \in \{0,1\} } } \frac{\mu(p^{k_1 - i})}{p^{3(k_1-i)/4}} \frac{\mu(p^{k_2 - j})}{p^{3(k_2-j)/4}} \varphi^*(p^{|k_1 - k_2|})\\ &= \bigg( \varphi^*(p^{|i-j|}) \big( 1 + p^{-3/2} \big) - \frac{\varphi^*(p^{|i-j+1|}) + \varphi^*(p^{|i-j-1|}) }{p^{3/4}} \bigg). \end{aligned} \end{align} $$
Here, we do not have the contribution coming from
$\mathcal {U}_K(K-1, K)$
or
$\mathcal {U}_K^{\top } (K, K-1)$
as we have assumed
$i, j \leq K-1$
. This assumption is necessary because we are considering the values
$k_1 = i+1$
and
$k_2 = j+1$
(both of which should remain
$\leq K$
).
First, let us consider the case
$i \geq j$
. Letting
$i-j = m \geq 0$
, (6.4) becomes
$$ \begin{align*} \begin{aligned} \mathcal{A}_K(i+m, i) &= \varphi^*(p^m) - p^{-3/4} \varphi^*(p^{|m-1|}) - p^{-3/4} \big( \varphi^*(p^{m+1}) - p^{-3/4} \varphi^*(p^m) \big) \\ &= p^{-3m/4} \beta - p^{-3/4} p^{-3(m+1)/4} \beta \\ &= \beta(1 - p^{-3/2}) p^{-3m/4}. \end{aligned} \end{align*} $$
Similarly, for
$j \geq i$
, we will obtain the same expression in terms of
$m = j-i$
. This proves Proposition 6.1 for
$1 \leq i,j \leq K-1$
.
Next, we consider the case when one of i or j equals K.
Claim
$\mathcal {A}_K(i,K) = \mathcal {A}_K(K, j) = 0$
, for all
$1 \leq i, j \leq K-1$
.
We revert to the first line of the expression (6.4). Letting
$m = K-i \geq 1$
, we obtain
$$ \begin{align*} \begin{aligned} \mathcal{A}_K(i, K) &= \sum\limits_{\substack{k_1 \in \{i, i+1\}\\ k_2 \in \{K-1, K\}}} \frac{\mu(p^{k_1 - i})}{p^{3(k_1 - i)/4}} \frac{\mu(p^{K-k_2})}{p^{3(K-k_2)/4}} \varphi^*(p^{|k_1 - k_2|})\\ &= - p^{-3/4} \varphi^*(p^{m-1}) + p^{-3/2} \varphi^*(p^{|m-2|}) + \varphi^*(p^m) - p^{-3/4} \varphi^*(p^{m-1}) \\ &= -p^{-3/4} \big( \varphi^*(p^{m-1}) - p^{-3/4} \varphi^*(p^{|m-2|}) \big) + \varphi^*(p^m) - p^{-3/4} \varphi^*(p^{m-1})\\ &= -p^{-3/4} p^{-3(m-1)/4} \beta + p^{-3m/4} \beta = 0. \end{aligned} \end{align*} $$
It similarly follows that
$\mathcal {A}_K(K, j) = 0$
for
$1 \leq j \leq K-1$
, proving the claim.
Next, we see that
$$ \begin{align*} \begin{aligned} \mathcal{A}_K(K, K) &= \sum\limits_{k_1, k_2 \in \{K-1, K\}} \frac{ \mu(p^{K-k_1})}{p^{3(K-k_1)/4}} \frac{\mu(p^{K-k_2})}{p^{3(K-k_2)/4}} \,\varphi^*(p^{|k_1 - k_2|}) \\ &= 1 - p^{-3/4} \varphi^*(p) -p^{-3/4} \big( \varphi^*(p) - p^{-3/4} \big)\\ &= \beta - p^{-3/4} \big( p^{-3/4} \beta \big) = \beta(1 - p^{-3/2}). \end{aligned} \end{align*} $$
This completes the proof of Proposition 6.1.
Now since
$n \mapsto n^{-3/4}$
is completely multiplicative, by the proof of Lemma 5.1, the matrix
$$ \begin{align*}\mathcal{B}_K=\left(\left( \frac{\operatorname{\mathrm{lcm}}(a,b)}{\gcd(a,b)}\right)^{-3/4}\right)_{a,b\in\{1,\ldots,p^K\}}\end{align*} $$
is positive definite for all K. Since the entries
$(i,j)$
with
$1\leq i,j\leq K-1$
of
$\mathcal {A}_K$
coincide with the ones of the matrix
$c\mathcal {B}_K$
for some positive constant c, and that the entries
$(i,K)$
and
$(K,j)$
of
$\mathcal {A}_K$
are all zero with a single exception at the entry
$(K,K)$
, by Sylvester’s criterion (Lemma 5.3), we conclude that the matrix
$\mathcal {A}_K$
is positive definite for all K.
Since
$\mathcal {A}_K= \mathcal {U}_K^{\top } \mathcal {M}_K \mathcal {U}_K$
, we have
$$ \begin{align*}\det(\mathcal{A}_K) = \det(\mathcal{U}_K)^2 \, \det(\mathcal{M}_K) = (1-p^{-3/2})^2 \, \det(\mathcal{M}_K). \end{align*} $$
This proves that
$\det (\mathcal {M}_K)>0$
, and by induction over K in Lemma 5.3,
$\mathcal {M}_K$
is positive definite for all K.
Acknowledgements
We would like to thank the referee for a careful revision and for his/her comments, suggestions, and corrections that improved this paper. This project started while the first author was a visiting Professor at Aix-Marseille Université, and he is thankful for their kind hospitality. The main bulk of this paper was built when the fourth author was a guest of the Aix-Marseille Université I2M laboratory. We thank this place for its support.
