Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fitchett, Stephanie
Harbourne, Brian
and
Holay, Sandeep
2001.
Resolutions of Fat Point Ideals Involving Eight General Points of P2.
Journal of Algebra,
Vol. 244,
Issue. 2,
p.
684.
Fitchett, Stephanie
2001.
On Bounding the Number of Generators for Fat Point Ideals on the Projective Plane.
Journal of Algebra,
Vol. 236,
Issue. 2,
p.
502.
Harbourne, Brian
Holay, Sandeep
and
Fitchett, Stephanie
2002.
Resolutions of ideals of quasiuniform fat point subschemes of 𝐏².
Transactions of the American Mathematical Society,
Vol. 355,
Issue. 2,
p.
593.
Chandler, Karen A.
2005.
The geometric interpretation of Fröberg–Iarrobino conjectures on infinitesimal neighbourhoods of points in projective space.
Journal of Algebra,
Vol. 286,
Issue. 2,
p.
421.
Guardo, Elena
and
Harbourne, Brian
2007.
Resolutions of ideals of any six fat points in P2.
Journal of Algebra,
Vol. 318,
Issue. 2,
p.
619.
Gimigliano, Alessandro
Harbourne, Brian
and
Idà, Monica
2008.
Betti numbers for fat point ideals in the plane: A geometric approach.
Transactions of the American Mathematical Society,
Vol. 361,
Issue. 2,
p.
1103.
Ballico, E.
and
Idà, M.
2008.
On the minimal free resolution for fat point schemes of multiplicity at most 3 in P2.
Journal of Pure and Applied Algebra,
Vol. 212,
Issue. 7,
p.
1756.
Bocci, Cristiano
and
Harbourne, Brian
2009.
The resurgence of ideals of points and the containment problem.
Proceedings of the American Mathematical Society,
Vol. 138,
Issue. 4,
p.
1175.
Peeva, I.
and
Stillman, M.
2009.
Open Problems on Syzygies and Hilbert Functions.
Journal of Commutative Algebra,
Vol. 1,
Issue. 1,
Gimigliano, Alessandro
Harbourne, Brian
and
Idà, Monica
2009.
The role of the cotangent bundle in resolving ideals of fat points in the plane.
Journal of Pure and Applied Algebra,
Vol. 213,
Issue. 2,
p.
203.
Geramita, A. V.
Harbourne, Brian
and
Migliore, Juan
2009.
Classifying Hilbert functions of fat point subschemes in ℙ2.
Collectanea mathematica,
Vol. 60,
Issue. 2,
p.
159.
Bocci, Cristiano
and
Harbourne, Brian
2009.
Comparing powers and symbolic powers of ideals.
Journal of Algebraic Geometry,
Vol. 19,
Issue. 3,
p.
399.
Lahyane, Mustapha
2010.
On the finite generation of the effective monoid of rational surfaces.
Journal of Pure and Applied Algebra,
Vol. 214,
Issue. 7,
p.
1217.
Hassanzadeh, Seyed Hamid
and
Simis, Aron
2012.
Plane Cremona maps: Saturation and regularity of the base ideal.
Journal of Algebra,
Vol. 371,
Issue. ,
p.
620.
Kalinin, Nikita
2017.
Tropical Approach to Nagata’s Conjecture in Positive Characteristic.
Discrete & Computational Geometry,
Vol. 58,
Issue. 1,
p.
158.
Tài Hà, Huy
and
Mantero, Paolo
2021.
Commutative Algebra.
p.
373.
Carlini, Enrico
Catalisano, Maria Virginia
Favacchio, Giuseppe
and
Guardo, Elena
2022.
Rational Normal Curves and Hadamard Products.
Mediterranean Journal of Mathematics,
Vol. 19,
Issue. 3,
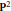 ${{\mathbf{P}}^{2}}$
${{\mathbf{P}}^{2}}$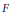 $F$ be a divisor on the blow-up
$F$ be a divisor on the blow-up 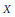 $X$ of
$X$ of 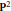 ${{\mathbf{P}}^{2}}$ at
${{\mathbf{P}}^{2}}$ at 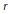 $r$ general points
$r$ general points 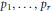 ${{p}_{1}},...,{{p}_{r}}$ and let
${{p}_{1}},...,{{p}_{r}}$ and let 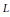 $L$ be the total transform of a line on
$L$ be the total transform of a line on 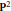 ${{\mathbf{P}}^{2}}$. An approach is presented for reducing the computation of the dimension of the cokernel of the natural map
${{\mathbf{P}}^{2}}$. An approach is presented for reducing the computation of the dimension of the cokernel of the natural map 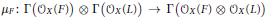 ${{\mu }_{F}}:\Gamma ({{\mathcal{O}}_{_{X}}}(F))\otimes \Gamma ({{\mathcal{O}}_{_{X}}}(L))\to \Gamma ({{\mathcal{O}}_{_{X}}}(F)\otimes {{\mathcal{O}}_{_{X}}}(L))$ to the case that
${{\mu }_{F}}:\Gamma ({{\mathcal{O}}_{_{X}}}(F))\otimes \Gamma ({{\mathcal{O}}_{_{X}}}(L))\to \Gamma ({{\mathcal{O}}_{_{X}}}(F)\otimes {{\mathcal{O}}_{_{X}}}(L))$ to the case that 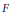 $F$ is ample. As an application, a formula for the dimension of the cokernel of
$F$ is ample. As an application, a formula for the dimension of the cokernel of 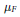 ${{\mu }_{_{F}}}$ is obtained when
${{\mu }_{_{F}}}$ is obtained when 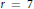 $r\,=\,7$, completely solving the problem of determining the modules in minimal free resolutions of fat point subschemes
$r\,=\,7$, completely solving the problem of determining the modules in minimal free resolutions of fat point subschemes 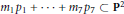 ${{m}_{1}}\,{{p}_{1}}\,+\,\cdot \cdot \cdot \,+\,{{m}_{7}}\,{{p}_{7}}\,\subset \,{{\mathbf{P}}^{2}}$. All results hold for an arbitrary algebraically closed ground field
${{m}_{1}}\,{{p}_{1}}\,+\,\cdot \cdot \cdot \,+\,{{m}_{7}}\,{{p}_{7}}\,\subset \,{{\mathbf{P}}^{2}}$. All results hold for an arbitrary algebraically closed ground field 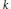 $k$.
$k$.