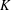 $K$-SPHERICAL FUNCTIONS ON ABELIAN SEMIGROUPS
$K$-SPHERICAL FUNCTIONS ON ABELIAN SEMIGROUPS
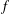 $f$-MAXIMAL SPACELIKE HYPERSURFACES IN CERTAIN WEIGHTED MANIFOLDS
$f$-MAXIMAL SPACELIKE HYPERSURFACES IN CERTAIN WEIGHTED MANIFOLDS
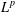 $L^{p}$–
$L^{p}$–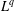 $L^{q}$ OFF-DIAGONAL ESTIMATES FOR THE ORNSTEIN–UHLENBECK SEMIGROUP: SOME POSITIVE AND NEGATIVE RESULTS
$L^{q}$ OFF-DIAGONAL ESTIMATES FOR THE ORNSTEIN–UHLENBECK SEMIGROUP: SOME POSITIVE AND NEGATIVE RESULTS
 $V$-HARMONIC MAPS AND THEIR APPLICATIONS
$V$-HARMONIC MAPS AND THEIR APPLICATIONS