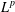Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T04:06:33.705Z Has data issue: false hasContentIssue false
  • English
  • Français

$L^{p}$–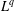$L^{q}$ OFF-DIAGONAL ESTIMATES FOR THE ORNSTEIN–UHLENBECK SEMIGROUP: SOME POSITIVE AND NEGATIVE RESULTS

Part of: Abstract harmonic analysis Groups and semigroups of linear operators, their generalizations and applications

Published online by Cambridge University Press:  06 February 2017

ALEX AMENTA  and
JONAS TEUWEN
ALEX AMENTA*
Affiliation:
Delft Institute of Applied Mathematics, Delft University of Technology, PO Box 5031, 2628 CD Delft, The Netherlands email [email protected]
JONAS TEUWEN
Affiliation:
Division of Radiation Oncology, Netherlands Cancer Institute/Antoni van Leeuwenhoek, Plesmanlaan 121, 1066 CX Amsterdam, The Netherlands Department of Imaging Physics, Optics Research Group, Delft University of Technology, PO Box 5031, 2628 CD Delft, The Netherlands email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate 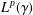$L^{p}(\unicode[STIX]{x1D6FE})$–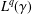$L^{q}(\unicode[STIX]{x1D6FE})$ off-diagonal estimates for the Ornstein–Uhlenbeck semigroup 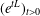$(e^{tL})_{t>0}$. For sufficiently large $t$ (quantified in terms of 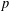$p$ and 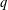$q$), these estimates hold in an unrestricted sense, while, for sufficiently small $t$, they fail when restricted to maximal admissible balls and sufficiently small annuli. Our counterexample uses Mehler kernel estimates.

Keywords

Ornstein–Uhlenbeck semigroupoff-diagonal estimatesMehler kernel

MSC classification

Primary: 47D06: One-parameter semigroups and linear evolution equations
Secondary: 43A99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 1 , August 2017 , pp. 154 - 161
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author acknowledges financial support from the Australian Research Council Discovery Grant DP120103692 and the ANR project ‘Harmonic analysis at its boundaries’ ANR-12-BS01-0013. The second author acknowledges partial financial support from the Netherlands Organisation for Scientific Research (NWO) by the NWO-VICI grant 639.033.604.

References

Auscher, P., ‘On necessary and sufficient conditions for L p -estimates of Riesz transforms associated to elliptic operators on ℝ n and related estimates’, Mem. Amer. Math. Soc. 186(871) (2007), xviii+75.Google Scholar
Auscher, P., Hofmann, S., Lacey, M., McIntosh, A. and Tchamitchian, P., ‘The solution of the Kato square root problem for second order elliptic operators on ℝ n ’, Ann. of Math. (2) 156 (2002), 633–654.CrossRefGoogle Scholar
Auscher, P. and Martell, J. M., ‘Weighted norm inequalities, off-diagonal estimates and elliptic operators part ii: off-diagonal estimates on spaces of homogeneous type’, J. Evol. Equ. 7(2) (2007), 265–316.Google Scholar
Axelsson, A., Keith, S. and McIntosh, A., ‘Quadratic estimates and functional calculi of perturbed Dirac operators’, Invent. Math. 163 (2006), 455–497.Google Scholar
Bakry, D., Bolley, F. and Gentil, I., ‘Dimension dependent hypercontractivity for Gaussian kernels’, Probab. Theory Related Fields 154(3–4) (2012), 845–874.CrossRefGoogle Scholar
Bakry, D., Bolley, F., Gentil, I. and Maheux, P., ‘Weighted Nash inequalities’, Rev. Mat. Iberoam. 28(3) (2012), 879–906.CrossRefGoogle Scholar
Mauceri, G. and Meda, S., ‘BMO and H 1 for the Ornstein–Uhlenbeck operator’, J. Funct. Anal. 252(1) (2007), 278–313.Google Scholar
Nelson, E., ‘A quartic interaction in two dimensions’, in: Mathematical Theory of Elementary Particles (Proc. Conf., Dedham, MA, 1965) (MIT Press, Cambridge, MA, 1966), 69–73.Google Scholar
Nelson, E., ‘Construction of quantum fields from Markoff fields’, J. Funct. Anal. 12 (1973), 97–112.CrossRefGoogle Scholar
Sjögren, P., ‘Operators associated with the Hermite semigroup—a survey’, in: Proceedings of the conference dedicated to Professor Miguel de Guzmán (El Escorial, 1996), J. Fourier Anal. Appl. 3 (1997), Supplement 1, 813–823.Google Scholar
Teuwen, J., ‘A note on Gaussian maximal functions’, Indag. Math. (N.S.) 26 (2015), 106–112.CrossRefGoogle Scholar
Teuwen, J., ‘On the integral kernels of derivatives of the Ornstein–Uhlenbeck semigroup’, Infin. Dimens. Anal. Quantum Probab. Relat. Top. 19 (2016), Article ID 1650030, 13 pages.Google Scholar
van Neerven, J. and Portal, P., ‘Finite speed of propagation and off-diagonal bounds for Ornstein–Uhlenbeck operators in infinite dimensions’, Ann. Mat. Pura Appl. (4) 195(6) (2016), 1889–1915.Google Scholar