Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T13:09:44.359Z Has data issue: false hasContentIssue false
  • English
  • Français

ITERATED LOGARITHM SPEED OF RETURN TIMES

Part of: Ergodic theory Topological dynamics

Published online by Cambridge University Press:  04 October 2017

ŁUKASZ PAWELEC Open the ORCID record for ŁUKASZ PAWELEC [Opens in a new window]
ŁUKASZ PAWELEC*
Affiliation:
Department of Mathematics and Mathematical Economics, Warsaw School of Economics, al. Niepodległości 162, 02–554 Warszawa, Poland email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a general setting of an ergodic dynamical system, we give a more accurate calculation of the speed of the recurrence of a point to itself (or to a fixed point). Precisely, we show that for a certain 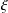$\unicode[STIX]{x1D709}$ depending on the dimension of the space, 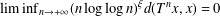$\liminf _{n\rightarrow +\infty }(n\log \log n)^{\unicode[STIX]{x1D709}}d(T^{n}x,x)=0$ almost everywhere and 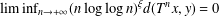$\liminf _{n\rightarrow +\infty }(n\log \log n)^{\unicode[STIX]{x1D709}}d(T^{n}x,y)=0$ for almost all $x$ and 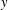$y$. This is done by assuming the exponential decay of correlations and making a weak assumption on the invariant measure.

Keywords

Poincaré theoremrecurrencedecay of correlationsshrinking target

MSC classification

Primary: 37A25: Ergodicity, mixing, rates of mixing
Secondary: 37B20: Notions of recurrence
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 3 , December 2017 , pp. 468 - 478
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Barreira, L. and Saussol, B., ‘Hausdorff dimension of measures via Poincaré recurrence’, Commun. Math. Phys. 219 (2001), 443–463.Google Scholar
Boshernitzan, M. D., ‘Quantitative recurrence results’, Invent. Math. 113 (1993), 617–631.Google Scholar
Boyarski, A. and Góra, P., Laws of Chaos: Invariant Measures and Dynamical Systems in One Dimension (Birkhäuser, Boston, 1997).Google Scholar
Mauldin, R. D. and Urbański, M., ‘Fractal measures for parabolic IFS’, Adv. Math. 136 (1998), 225–253.Google Scholar
Mauldin, R. D. and Urbański, M., Graph Directed Markov Systems: Geometry and Dynamics of Limit Sets (Cambridge University Press, Cambridge, 2003).Google Scholar
Persson, T. and Rams, M., ‘On shrinking targets for piecewise expanding interval maps’, Ergod. Th. & Dynam. Syst. 37 (2017), 646–663.CrossRefGoogle Scholar
Przytycki, F. and Urbański, M., Conformal Fractals: Ergodic Theory Methods (Cambridge University Press, Cambridge, 2010).Google Scholar
Sullivan, D., ‘Conformal dynamical systems’, in: Geometric Dynamics, Lecture Notes in Mathematics, 1007 (ed. Palis, J.) (Springer, Berlin, Heidelberg, 1983), 725–752.Google Scholar
Urbański, M., ‘Recurrence rates for loosely Markov dynamical systems’, J. Aust. Math. Soc. 82 (2007), 39–57.Google Scholar