Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T13:47:14.948Z Has data issue: false hasContentIssue false
  • English
  • Français

ON MULTIPLIERS BETWEEN SOME SPACES OF HOLOMORPHIC FUNCTIONS

Part of: Topological linear spaces and related structures Spaces and algebras of analytic functions Harmonic analysis in one variable

Published online by Cambridge University Press:  29 March 2017

BARTOSZ STANIÓW Open the ORCID record for BARTOSZ STANIÓW [Opens in a new window]
BARTOSZ STANIÓW*
Affiliation:
Faculty of Mathematics and Computer Sciences, Adam Mickiewicz University in Poznań, Poland email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study function multipliers between spaces of holomorphic functions on the unit disc of the complex plane generated by symmetric sequence spaces. In the case of sequence 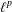$\ell ^{p}$ spaces we recover Nikol’skii’s results [‘Spaces and algebras of Toeplitz matrices operating on 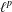$\ell ^{p}$’, Sibirsk. Mat. Zh.7 (1966), 146–158].

Keywords

holomorphic functionsmultiplierssymmetric sequence spacesconvolution

MSC classification

Primary: 46A45: Sequence spaces (including Köthe sequence spaces)
Secondary: 42A45: Multipliers 30H99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 1 , August 2017 , pp. 146 - 153
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Defant, A., Mastyło, M. and Michels, C., ‘Summing inclusion maps between symmetric sequence spaces’, Trans. Amer. Math. Soc. 354(11) (2002), 4473–4492.CrossRefGoogle Scholar
Fernandez-Cabrera, L. M., ‘Inclusion indices of function spaces and applications’, Math. Proc. Cambridge Philos. Soc. 136(3) (2004), 665–674.CrossRefGoogle Scholar
Kantorovich, L. V. and Akilov, G. P., Functional Analysis, 2nd revised edn (Nauka, Moscow, 1977), (in Russian); English translation, Pergamon Press, Oxford, 1982.Google Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces, Vol. I (Springer, Berlin, 1997).Google Scholar
Nikol’skii, N. K., ‘Spaces and algebras of Toeplitz matrices operating on ℓ p ’, Sibirsk. Mat. Zh. 7 (1966), 146–158.Google Scholar
Schur, I., ‘Über Potenzreihen, die im Innern des Einheitskreises baschränkt sind’, J. reine angew. Math. 147 (1917), 205–232.CrossRefGoogle Scholar
Sukochev, F. A. and Tomskova, A. A., ‘Schur multipliers associated with symmetric sequence spaces’, Mat. Zametki 92(6) (2012), 939–942; (in Russian); English translation, Math. Notes 92(5–6) (2012), 830–833.Google Scholar
Zygmund, A., Trigonometric Series, Vol. I (Cambridge University Press, Cambridge, 1959).Google Scholar