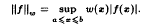Research Article
Nearly integral homomorphisms of commutative rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-12
-
- Article
-
- You have access
- Export citation
Groups whose three-generator subgroups are free
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 163-174
-
- Article
-
- You have access
- Export citation
Almost complex structures on the orthogonal twistor bundle
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 337-344
-
- Article
-
- You have access
- Export citation
Non commutative convolution measure algebras with no proper L-ideals
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 13-23
-
- Article
-
- You have access
- Export citation
Asymptotic behaviour of solutions to neutral functional differential equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 345-355
-
- Article
-
- You have access
- Export citation
Generators for the bounded automorphisms of infinite-rank free nilpotent groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 175-187
-
- Article
-
- You have access
- Export citation
Decay estimates for some nonlinear second order ordinary differential equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 25-35
-
- Article
-
- You have access
- Export citation
The heredity measure of an algebra
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 189-197
-
- Article
-
- You have access
- Export citation
Periodic solutions of a second order nonlinear differential equation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 357-361
-
- Article
-
- You have access
- Export citation
Embedding and representation theorems for clones and varieties
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 199-205
-
- Article
-
- You have access
- Export citation
Bounded measurable simultaneous monotone approximation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 37-48
-
- Article
-
- You have access
- Export citation
On a problem of Szász
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 363-364
-
- Article
-
- You have access
- Export citation
Automorphisms of nilpotent-by-abelian groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 207-213
-
- Article
-
- You have access
- Export citation
Constructing lattice-ordered fields and division rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 365-369
-
- Article
-
- You have access
- Export citation
On Witt's dimension formula for free Lie algebras and a theorem of Klyachko
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 49-57
-
- Article
-
- You have access
- Export citation
Third Engel groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 215-230
-
- Article
-
- You have access
- Export citation
Identities for existence varieties of regular semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 59-77
-
- Article
-
- You have access
- Export citation
Covers and complements in the subalgebra lattice of a Boolean algebra
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 371-379
-
- Article
-
- You have access
- Export citation
Some groups all of whose proper verbal quotients are relatively free
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 231-234
-
- Article
-
- You have access
- Export citation
Data types in distributive categories
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 79-82
-
- Article
-
- You have access
- Export citation