The following result has been established by Stadje and Gross:

THEOREM. If 〈X, d〉 is a compact connected metric space, then there is a unique positive real number a(〈X, d〉) with the property that for each natural number n, and for all {x1, x2, …, xn} ⊂ X, there exists y ∈ X for which

We give a simple proof of the fact that compact, connected topological spaces have the “average distance property”. For a metric space (X, d), this asserts the existence of a unique number a = a(X) such that, given finitely many points x1, …, xn ∈ X, then there is some y ∈ X with

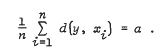
We examine the possible values of a(X) , for subsets of finite dimensional normed spaces. For example, if diam(X) denotes the diameter of some compact, convex set in a euclidean space, then a(X) ≤ diam(X)/√2 . On the other hand, a(X)/diam(X) can be arbitrarily close to 1 , for non-convex sets in euclidean spaces of sufficiently large dimension.

Let G be a graph. With every connected subgraph of G, let us associate a weight (Wα and with every spanning subgrapha or cover) C of G, a weight

where αi (i = 1, 2, …, n) are the components of C. The subgraph polynomial of G is

where the summation is taken over all the spanning subgraphs in G.

The basic properties of subgraph polynomials are given, expressions for the subgraph polynomials of multigraphs and pseudographs are derived, and the chromatic and dichromatic polynomials are shown to be special cases of the subgraph polynomial.

We call a group G cyclically separated if for any given cyclic subgroup B in G and subgroup A of finite index in B, there exists a normal subgroup N of G of finite index such that N ∩ B = A. This is equivalent to saying that for each element x ∈ G and integer n ≥ 1 dividing the order o(x) of x, there exists a normal subgroup N of G of finite index such that Nx has order n in G/N. As usual, if x has infinite order then all integers n ≥ 1 are considered to divide o(x). Cyclically separated groups, which are termed “potent groups” by some authors, form a natural subclass of residually finite groups and finite cyclically separated groups also form an interesting class whose structure we are able to describe reasonably well. Construction of finite soluble cyclically separated groups is given explicitly. In the discussion of infinite soluble cyclically separated groups we meet the interesting class of Fitting isolated groups, which is considered in some detail. A soluble group G of finite rank is Fitting isolated if, whenever H = K/L (L ⊲ K ≤ G) is a torsion-free section of G and F(H) is the Fitting subgroup of H then H/F(H) is torsion-free abelian. Every torsion-free soluble group of finite rank contains a Fitting isolated subgroup of finite index.

A simple change of the operation in a commutative semigroup leads to a groupoid. It is shown that it has no finite basis for its laws.

This paper provides an example of a non-abelian 2-group with a non-abelian automorphism group in which every automorphism is central.