Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-09T14:36:07.157Z Has data issue: false hasContentIssue false
  • English
  • Français

On a class of polynomials associated with the subgraphs of a graph and its application to chromatic and dichromatic polynomials

Published online by Cambridge University Press:  17 April 2009

E.J. Farrell
E.J. Farrell
Affiliation:
Department of Mathematics, University of West Indies, St Augustine, Trinidad, West Indies.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a graph. With every connected subgraph of G, let us associate a weight (Wα and with every spanning subgrapha or cover) C of G, a weight

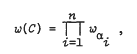
where αi (i = 1, 2, …, n) are the components of C. The subgraph polynomial of G is

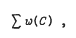
where the summation is taken over all the spanning subgraphs in G.

The basic properties of subgraph polynomials are given, expressions for the subgraph polynomials of multigraphs and pseudographs are derived, and the chromatic and dichromatic polynomials are shown to be special cases of the subgraph polynomial.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 26 , Issue 3 , December 1982 , pp. 343 - 354
Copyright
Copyright © Australian Mathematical Society 1982

References

[1]Farrell, E.J., “On a general class of graph polynomials”, J. Combin. Theory Ser. B 26 (1979), 111–122.CrossRefGoogle Scholar
[2]Harary, Frank, Graph theory (Addison-Wesley,, Reading, Massachusetts; Menlo Park, California; London; 1969).CrossRefGoogle Scholar
[3]Read, Ronald C., “An introduction to chromatic polynomials”, J. Combin. Theory 4 (1968), 52–71.CrossRefGoogle Scholar
[4]Tutte, W.T., “On dichromatic polynomials”, J. Combin. Theory 2 (1967), 301–320.CrossRefGoogle Scholar
[5]Whitney, Hassler, “A logical expansion in mathematics”, Bull. Amer. Math. Soc. 38 (1932), 572–579.CrossRefGoogle Scholar