Research Article
Universally Incomparable Ring-Homomorphisms
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 289-302
-
- Article
-
- You have access
- Export citation
Algebras generated by symmetric idempotents
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 303-308
-
- Article
-
- You have access
- Export citation
Automorphism groups of orthomodular lattices
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 309-313
-
- Article
-
- You have access
- Export citation
A Density problem for Hardy spaces of almost periodic functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 315-327
-
- Article
-
- You have access
- Export citation
Univalent functions with univalent Gelfond-Leontev derivatives
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 329-348
-
- Article
-
- You have access
- Export citation
Generalization of Leader's fixed point principle
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 349-356
-
- Article
-
- You have access
- Export citation
An integral characterization of Euclidean space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 357-364
-
- Article
-
- You have access
- Export citation
Monadic representability of certain binary relations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 365-376
-
- Article
-
- You have access
- Export citation
Oscillations in linear systems of differential-difference equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 377-387
-
- Article
-
- You have access
- Export citation
Graphs with Eulerian chains
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 389-399
-
- Article
-
- You have access
- Export citation
Free products of locally indicable groups with a single relator
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 401-404
-
- Article
-
- You have access
- Export citation
Decompositions of graphs of modules over semisimple rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 405-413
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
Epimorphisms and semigroup varieties
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 415-417
-
- Article
-
- You have access
- Export citation
Recursive properties of isomorphism types
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 419-421
-
- Article
-
- You have access
- Export citation
Composite graphs with stability index one
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 423-424
-
- Article
-
- You have access
- Export citation
Biordered sets of semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 425-427
-
- Article
-
- You have access
- Export citation
Mathematical modelling of rate-limiting mechanisms of pyritic oxidation in overburden dumps
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 429-430
-
- Article
-
- You have access
- Export citation
Corrigendum
Cardinality of discrete subsets of a topological space: Corrigendum
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 431
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 29 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f6
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 29 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

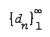 be a nondecreasing sequence of positive numbers. We consider Gelfond-Leontev derivative
be a nondecreasing sequence of positive numbers. We consider Gelfond-Leontev derivative 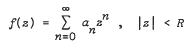 , defined by
, defined by 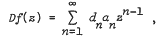 for univalence and growth properties, and extend some results of Shah and Trimble. Set
for univalence and growth properties, and extend some results of Shah and Trimble. Set 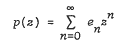 . Let
. Let 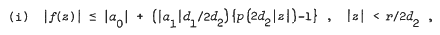
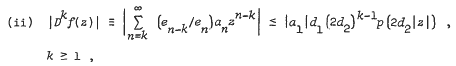
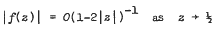 .
.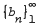 is a sequence of positive numbers satisfying and inequality, and it is shown that all functions in this class along with all their Gelfond–Leontev successive derivatives are regular and univalent in
is a sequence of positive numbers satisfying and inequality, and it is shown that all functions in this class along with all their Gelfond–Leontev successive derivatives are regular and univalent in