Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T02:11:16.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted convolutions of certain polynomials

Published online by Cambridge University Press:  17 April 2009

Massoud Jahangiri
Massoud Jahangiri
Affiliation:
Department of MathematicaUniversity of CaliforniaDavis CA 95616United States of America
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For α ≥ 0 and β ≥ 0, let K(β) consist of those functions f(z), analytic and non-zero in |z| < 1, such that for θ1 < θ2 < θ1 + 2π and 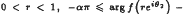. It is conjectured that for 1 ≤ α ≤ β and α an integer, the weighted convolution of polynomials having their zeros on |z| = 1 and belonging to K(α, β), also belong to K(α, β). This conjecture is known to be true for the case α = 1, which leads to an alternative proof for the generalised Polya-Schoenberg conjecture. The case α = 2 is also known to be true for cubic polynomials. We prove the conjecture for certain quartic polynomials when 2 ≤ α ≤ 4.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 40 , Issue 3 , December 1989 , pp. 397 - 405
Copyright
Copyright © Australian Mathematical Society 1989

References

[1]Jahangiri, M., ‘A gap condition for the zeros of certain polynomials in Kaplan classes K(α, β)’, Mathematika 34 (1987), 53–63.CrossRefGoogle Scholar
[2]Lewis, J.L., ‘Convolutions of Starlike functions’, Indiana Univ. Math. J. 27 (1978), 671–688.CrossRefGoogle Scholar
[3]Polya, G. and Schoenberg, I.J., ‘Remarks on de la Vallee Poussin Means and convex conformal maps of the circle’, Pacific J. Math. 8 (1958), 295–334.CrossRefGoogle Scholar
[4]Ruscheweyh, St., ‘Linear operators between classes of prestarlike functions’, Comment. Math. Helv. 52 (1977), 497–509.CrossRefGoogle Scholar
[5]Ruscheweyh, St., Convolutions in geometric function theory Sém. Math. Sup. (L Presses, De L'Universite Dc Montréal, Montreal, Que., 1982).Google Scholar
[6]Ruscheweyh, St. and Sheil-Small, T.B., ‘Hadamard products of Schlicht functions and the Polya-Schoenberg conjecture’, Comment. Math. Helv. 48 (1973), 119–135.CrossRefGoogle Scholar
[7]Sheil-Small, T.B., ‘The Hadamard product and linear transofrmations of classes of analytic functions’, J. Analyse Math. 34 (1978), 204–239.CrossRefGoogle Scholar
[8]Sheil-Small, T.B., ‘Coefficients and integral means of some classes of analytic functions’, Proc. Amer. Math. Soc. 88 (1983), 275–282.CrossRefGoogle Scholar
[9]Sheil-Small, T.B., ‘Some remarks on Bazilevic functions’, J. Analyse Math. 43 (1983/1984), 1–11.CrossRefGoogle Scholar
[10]Suffridge, T.J., ‘Starlike functions as limits of polynomials’: Advances in Complex Function Theory.: Lecture Notes in Math 505 (Springer-Verlag, New York). pp. 164–203.CrossRefGoogle Scholar