Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T04:06:32.835Z Has data issue: false hasContentIssue false
  • English
  • Français

Lebesgue constants for double Hausdorff means

Published online by Cambridge University Press:  17 April 2009

F. Ustina
F. Ustina
Affiliation:
Department of Mathematics, University of Alberta, Edmonton, Canada T6G 2G1.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

As is well known, the divergence of the set of constants known as the Lebesgue constants corresponding to a particular method of summability implies the existence of a continuous, periodic function whose Fourier series, summed by the method, diverges at a point, and of another such function the sums of whose Fourier series converge everywhere but not uniformly in the neighborhood of some point.

In 1961, Lorch and Newman established that if L(n; g) is the nth Lebesgue constant for the Hausdorff summability method corresponding to the weight function g(u), then

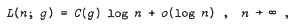
where

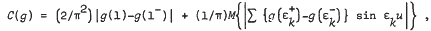
where the summation is taken over the jump discontinuities {εk} of g(u) and M{f(u)} denotes the mean value of the almost periodic function f(u).

In this paper, a partial extension of this result to the two dimensional analogue is obtained. This extension is summarized in Theorem 1.3.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 31 , Issue 2 , April 1985 , pp. 199 - 214
Copyright
Copyright © Australian Mathematical Society 1985

References

[1]Adams, C.R., “Hausdorff transformations for double sequences”, Bull. Amer. Math. Soc. 39 (1933), 303–312.Google Scholar
[2]Adams, C.R., “On definitions of bounded variation for functions of two variables”, Trans. Amer. Math. Soc. 35 (1933), 824–854.Google Scholar
[3]Livingston, A.E., “The Lebesgue constants for Euler (E, p) summation of Fourier series”, Duke Math. J. 21 (1951), 309–314.Google Scholar
[4]Lorch, L. and Newman, D.J., “The Lebesgue constants for regular Hausdorff methods”, Canad. J. Math. 13 (1961), 283–298.Google Scholar
[5]Szász, O., “Gibbs phenomenon for Hausdorff means”, Trans. Amer. Math. Soc. 28 (1926), 50–73.Google Scholar
[6]Ustina, F., “Gibbs phenomenon for the Hausdorff means of double sequences”, J. Austral. Math. Soc. 11 (1970), 169–185.CrossRefGoogle Scholar