As is well known, the divergence of the set of constants known as the Lebesgue constants corresponding to a particular method of summability implies the existence of a continuous, periodic function whose Fourier series, summed by the method, diverges at a point, and of another such function the sums of whose Fourier series converge everywhere but not uniformly in the neighborhood of some point.
In 1961, Lorch and Newman established that if L(n; g) is the nth Lebesgue constant for the Hausdorff summability method corresponding to the weight function g(u), then
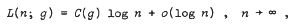
where
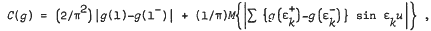
where the summation is taken over the jump discontinuities {εk} of g(u) and M{f(u)} denotes the mean value of the almost periodic function f(u).
In this paper, a partial extension of this result to the two dimensional analogue is obtained. This extension is summarized in Theorem 1.3.