Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T23:50:11.892Z Has data issue: false hasContentIssue false
  • English
  • Français

Extensions of finite nilpotent groups

Published online by Cambridge University Press:  17 April 2009

John Poland
John Poland
Affiliation:
Carleton University, Ottawa, Canada.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If G is a finite group and P is a group-theoretic property, G will be called P-max-core if for every maximal subgroup M of G, M/MG has property P where MG = ∩ 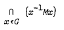is the core of M in G. In a joint paper with John D. Dixon and A.H. Rhemtulla, we showed that if p is an odd prime and G is (p-nilpotent)-max-core, then G is p-solvable, and then using the techniques of the theory of solvable groups, we characterized nilpotent-max-core groups as finite nilpotent-by-nilpotent groups. The proof of the first result used John G. Thompson's p-nilpotency criterion and hence required p > 2. In this paper I show that supersolvable-max-core groups (and hence (2-nilpotent)-max-core groups) need not be 2-solvable (that is, solvable). Also I generalize the second result, among others, and characterize (p-nilpotent)-max-core groups (for p an odd prime) as finite nilpotent-by-(p-nilpotent) groups.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 2 , Issue 2 , April 1970 , pp. 267 - 274
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]Baer, Reinhold, “Classes of finite groups and their properties”, Illinois J. Math. 1 (1957), 115–187.CrossRefGoogle Scholar
[2]Carter, Roger and Hawkes, Trevor, “The F-normalizers of a finite soluble group”, J. Algebra 5 (1967), 175–202.CrossRefGoogle Scholar
[3]Dickson, Leonard Eugene, Linear groups, with an exposition of the Galois field theory (Teubner, Leipzig, 1901; reprinted Dover, New York, 1958).Google Scholar
[4]Dixon, John D., Poland, John and Rhemtulla, A.H., “A generalization of hamiltonian and nilpotent groups”, Math. Z. 112 (1969), 335–339.CrossRefGoogle Scholar
[5]Gorenstein, Daniel, Finite groups (Harper and Row, New York, Evanston, London, 1968).Google Scholar
[6]Huppert, Bertram, Endliche Gruppen I (Springer-Verlag, Berlin, Heidelberg, New York, 1967).CrossRefGoogle Scholar
[7]Lausch, H., “Formations of π-soluble groups”, J. Austral. Math. Soc. 10 (1969), 241–250.CrossRefGoogle Scholar
[8]Suzuki, Michio, “On a class of doubly transitive groups”, Ann. of Math. (2) 75 (1962), 105–145.CrossRefGoogle Scholar