Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T02:33:24.405Z Has data issue: false hasContentIssue false
  • English
  • Français

CHARACTERISATIONS OF HARDY GROWTH SPACES WITH DOUBLING WEIGHTS

Part of: Harmonic analysis in one variable Spaces and algebras of analytic functions

Published online by Cambridge University Press:  12 May 2014

EVGUENI DOUBTSOV
EVGUENI DOUBTSOV*
Affiliation:
St. Petersburg Department of V.A. Steklov Mathematical Institute, Fontanka 27, St. Petersburg 191023, Russia email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 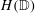$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}H(\mathbb{D})$ denote the space of holomorphic functions on the unit disc 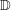$\mathbb{D}$. Given 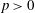$p>0$ and a weight 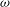$\omega $, the Hardy growth space 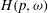$H(p, \omega )$ consists of those 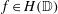$f\in H(\mathbb{D})$ for which the integral means 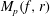$M_p(f,r)$ are estimated by 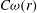$C\omega (r)$, 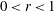$0<r<1$. Assuming that 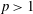$p>1$ and 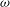$\omega $ satisfies a doubling condition, we characterise 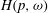$H(p, \omega )$ in terms of associated Fourier blocks. As an application, extending a result by Bennett et al. [‘Coefficients of Bloch and Lipschitz functions’, Illinois J. Math. 25 (1981), 520–531], we compute the solid hull of 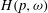$H(p, \omega )$ for 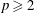$p\ge 2$.

Keywords

Hardy growth spacedoubling weight

MSC classification

Secondary: 30H10: Hardy spaces 42A55: Lacunary series of trigonometric and other functions; Riesz products
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 2 , October 2014 , pp. 275 - 282
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Abakumov, E. and Doubtsov, E., ‘Reverse estimates in growth spaces’, Math. Z. 271 (2012), 399–413.CrossRefGoogle Scholar
Anderson, J. M. and Shields, A. L., ‘Coefficient multipliers of Bloch functions’, Trans. Amer. Math. Soc. 224 (1976), 255–265.Google Scholar
Bennett, G., Stegenga, D. A. and Timoney, R. M., ‘Coefficients of Bloch and Lipschitz functions’, Illinois J. Math. 25 (1981), 520–531.CrossRefGoogle Scholar
Eikrem, K. S., ‘Hadamard gap series in growth spaces’, Collect. Math. 64 (2013), 1–15.CrossRefGoogle Scholar
Eikrem, K. S. and Malinnikova, E., ‘Radial growth of harmonic functions in the unit ball’, Math. Scand. 110 (2012), 273–296.Google Scholar
Girela, D., Pavlović, M. and Peláez, J. Á., ‘Spaces of analytic functions of Hardy–Bloch type’, J. Anal. Math. 100 (2006), 53–81.Google Scholar
Grosse-Erdmann, K.-G., Lecture Notes in Mathematics, 1679 (Springer-Verlag, Berlin, 1998).Google Scholar
Mateljević, M. and Pavlović, M., ‘L p-behaviour of the integral means of analytic functions’, Studia Math. 77 (1984), 219–237.Google Scholar
Shields, A. L. and Williams, D. L., ‘Bonded projections, duality, and multipliers in spaces of analytic functions’, Trans. Amer. Math. Soc. 162 (1971), 287–302.Google Scholar
Shields, A. L. and Williams, D. L., ‘Bounded projections and the growth of harmonic conjugates in the unit disc’, Michigan Math. J. 29 (1982), 3–25.CrossRefGoogle Scholar