Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T02:10:43.546Z Has data issue: false hasContentIssue false
  • English
  • Français

APPLICATIONS OF LERCH’S THEOREM TO PERMUTATIONS OF QUADRATIC RESIDUES

Part of: Elementary number theory Algebraic number theory: global fields Sequences and sets Combinatorics

Published online by Cambridge University Press:  10 July 2019

LI-YUAN WANG Open the ORCID record for LI-YUAN WANG [Opens in a new window]  and
HAI-LIANG WU Open the ORCID record for HAI-LIANG WU [Opens in a new window]
LI-YUAN WANG
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, People’s Republic of China email [email protected]
HAI-LIANG WU*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, People’s Republic of China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $n$ be a positive integer and $a$ an integer prime to $n$. Multiplication by $a$ induces a permutation over 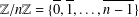$\mathbb{Z}/n\mathbb{Z}=\{\overline{0},\overline{1},\ldots ,\overline{n-1}\}$. Lerch’s theorem gives the sign of this permutation. We explore some applications of Lerch’s result to permutation problems involving quadratic residues modulo 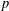$p$ and confirm some conjectures posed by Sun [‘Quadratic residues and related permutations and identities’, Preprint, 2018, arXiv:1809.07766]. We also study permutations involving arbitrary 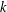$k$th power residues modulo 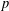$p$ and primitive roots modulo a power of 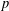$p$.

Keywords

Zolotarev’s lemmapermutationquadratic residueLerch’s theoremprimitive root

MSC classification

Primary: 11A15: Power residues, reciprocity
Secondary: 05A05: Permutations, words, matrices 11A07: Congruences; primitive roots; residue systems 11B75: Other combinatorial number theory 11R11: Quadratic extensions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 3 , December 2019 , pp. 362 - 371
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

This research was supported by the National Natural Science Foundation of China (grant no. 11571162).

References

Brunyate, A. and Clark, P. L., ‘Extending the Zolotarev–Frobenius approach to quadratic reciprocity’, Ramanujan J. 37 (2015), 25–50.Google Scholar
Cohen, H., A Course in Computational Algebraic Number Theory, Graduate Texts in Mathematics, 138 (Springer, New York, 1993).Google Scholar
Kohl, S., Question 302865 in MathOverflow, solved by F. Ladisch and F. Petrov, available at https://mathoverflow.net/questions/302865/.Google Scholar
Lerch, M., ‘Sur un théorème de Zolotarev’, Bull. Intern. Acad. François Joseph 3 (1896), 34–37.Google Scholar
Mordell, L. J., ‘The congruence ((p - 1)/2)! ≡±1(mod p)’, Amer. Math. Monthly 68 (1961), 145–146.Google Scholar
Pan, H., ‘A remark on Zolotarev’s theorem’, Preprint, 2006, arXiv:0601026.Google Scholar
Sun, Z. W, ‘Quadratic residues and related permutations and identities’, Preprint, 2018, arXiv:1809.07766.Google Scholar
Szekely, G. J. (ed), Contests in Higher Mathematics (Springer, New York, 1996).Google Scholar
Zolotarev, G., ‘Nouvelle démonstration de la loi de réciprocité de Legendre’, Nouvelles Ann. Math. 11 (1872), 354–362.Google Scholar