Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-16T19:54:49.251Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE REGULARITY OF CHARACTER DEGREE GRAPHS

Part of: Graph theory Representation theory of groups

Published online by Cambridge University Press:  08 March 2019

Z. SAYANJALI Open the ORCID record for Z. SAYANJALI [Opens in a new window] ,
Z. AKHLAGHI Open the ORCID record for Z. AKHLAGHI [Opens in a new window]  and
B. KHOSRAVI Open the ORCID record for B. KHOSRAVI [Opens in a new window]
Z. SAYANJALI
Affiliation:
Faculty of Mathematics and Computer Science, Amirkabir University of Technology (Tehran Polytechnic), 15914 Tehran, Iran email [email protected]
Z. AKHLAGHI*
Affiliation:
Faculty of Mathematics and Computer Science, Amirkabir University of Technology (Tehran Polytechnic), 15914 Tehran, Iran email [email protected]
B. KHOSRAVI
Affiliation:
Faculty of Mathematics and Computer Science, Amirkabir University of Technology (Tehran Polytechnic), 15914 Tehran, Iran email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 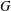$G$ be a finite group and let 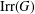$\text{Irr}(G)$ be the set of all irreducible complex characters of 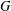$G$. Let 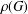$\unicode[STIX]{x1D70C}(G)$ be the set of all prime divisors of character degrees of 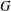$G$. The character degree graph 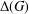$\unicode[STIX]{x1D6E5}(G)$ associated to 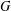$G$ is a graph whose vertex set is 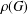$\unicode[STIX]{x1D70C}(G)$, and there is an edge between two distinct primes 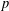$p$ and 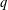$q$ if and only if 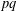$pq$ divides 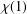$\unicode[STIX]{x1D712}(1)$ for some 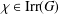$\unicode[STIX]{x1D712}\in \text{Irr}(G)$. We prove that 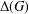$\unicode[STIX]{x1D6E5}(G)$ is 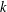$k$-regular for some natural number 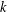$k$ if and only if 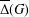$\overline{\unicode[STIX]{x1D6E5}}(G)$ is a regular bipartite graph.

Keywords

finite groupscharacter degree graph

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 3 , December 2019 , pp. 428 - 433
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Akhlaghi, Z., Casolo, C., Dolfi, S., Pacifici, E. and Sanus, L., ‘On the character degree graph of finite groups’, Annali di Mat. Pura Appl., to appear.Google Scholar
Akhlaghi, Z., Dolfi, S., Pacifici, E. and Sanus, L., ‘Bounding the number of vertices in the degree graph of a finite group’, Preprint, 2018, arXiv:1811.01674.Google Scholar
Huppert, B., Character Theory of Finite Groups (de Gruyter, Berlin, 2011).Google Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, New York, 1976).Google Scholar
Tong-Viet, H. P., ‘Finite groups whose prime graphs are regular’, J. Algebra 397 (2014), 18–31.Google Scholar
White, D. L., ‘Degree graphs of simple groups’, Rocky Mountain J. Math. 39 (2009), 1713–1739.Google Scholar
Zsigmondy, K., ‘Zur Theorie der Potenzreste’, Monatsh. Math. Phys. 3 (1892), 265–284.Google Scholar
Zuccari, C. P. M., ‘Regular character degree graphs’, J. Algebra 353 (2014), 215–224.Google Scholar