The present paper considers the present value, Z(t), of a series of cashflows up to some time t. More specifically, the cashflows and the interest rate process will often be stochastic and not necessarily independent of one another or through time. We discuss under what circumstances Z(t) will converge almost surely to some finite value as t→∞. This problem has previously been considered by Dufresne (1990) who provided a sufficient condition for almost sure convergence of Z(t) (the Root Test) and then proceeded to consider some specific examples of such processes. Here, we develop Dufresne's work and show that the sufficient condition for convergence can be proved to hold for quite a general class of model which includes the growing number of Office Models with stochastic cashflows.

Some practical applications of Sundt's (1992) generalized class of counting distributions are discussed. The numerical stabilities of some recursive formulas in Sundt's class are investigated.

Several countries have made community rating mandatory for certain lines of insurance, particularly health insurance. This paper offers a theoretical solution to the problem of designing equalisation schemes to support community rating in a market where different insurers are selling different benefit plans. The criterion chosen is that an equalisation scheme should minimise the opportunities for arbitrage between insurers, which community rating otherwise would generate. Several possible measures of arbitrage are presented, and the optimal schemes are compared against data from Australian health insurers. Finally, the approach is extended to partial community rating, for example unisex rating.

In this paper we study a transform introduced by De Pril (1989) for recursive evaluation of convolutions of counting distributions with a positive probability in zero. We discuss some cases where the evaluation of this transform is simplified and relate the transform to infinitely divisible distributions. Finally we discuss an algorithm presented by Dhaene & Vandebroek (1994) for recursive evaluation of convolutions.

We investigate the usual method of discretizing loss reserving data by calendar year and show how this procedure may introduce fluctuations in the delay probabilities. These fluctuations, when treated as random fluctuations, possess a special correlation structure and we present a simple credibility method accounting for these fluctuations. The results are illustrated by a numerical example.

The set of efficient portfolios in an asset liability model is discussed in detail. The occurence of liabilities leads to a parallel shift of the efficient set. Under an appropriate assumption, the shift vector can be decomposed in different components. For the special case, where the investor is a pension fund, it is shown how shortfall constraints can be reconciled with efficiency. Finally, optimality conditions for the market portfolio are derived.

In this paper we compare ruin functions for two risk processes with respect to stochastic ordering, stop-loss ordering and ordering of adjustment coefficients. The risk processes are as follows: in the Markov-modulated environment and the associated averaged compound Poisson model. In the latter case the arrival rate is obtained by averaging over time the arrival rate in the Markov modulated model and the distribution of the claim size is obtained by averaging the ones over consecutive claim sizes.

In practical applications of Credibility Theory the structure parameters usually have to be estimated from the data. This leads to an estimator of the a posteriori mean which is often biased and where the credibility factor depends on the data. A more coherent approach to the problem would be to also treat the unknown parameters as random variables and to simultaneously estimate the a posteriori mean and the structure parameters. Different statistical models are proposed which allow for such a solution. These models all lead to an estimation of the posterior mean which is a weighted average of the prior mean and of the observed mean, the weights depending on the observations.

This paper is devoted to the study of the initial reserve, as a function of the retention limit, needed to assure that the probability of ruin, at the end of a certain period of time, is not higher than an agreed value, for an excess of loss treaty. To assess the probability of ruin, the normal and the normal power approximation are used. It is shown that the initial reserve is not in general an increasing function of the retention, having a minimum under fair assumptions.

In this paper we present a stable recursive algorithm for the calculation of the probability of ultimate ruin in the classical risk model. We also present stable recursive algorithms for the calculation of the joint and marginal distributions of the surplus prior to ruin and the severity of ruin. In addition we present bounds for these distributions.

The paper extends earlier results by demonstrating that there is an optimal range of values for the period for amortizing valuation surpluses or deficiencies, in the case when there is a one year time delay between fixing a contribution rate and the accounting information about current fund levels. The optimal range is compared for the cases where there is no time delay and there is a one year time delay.

In the classical Bayesian approach to credibility the claims are conditionally independent and identically distributed random variables, with common density f(x, ϑ). The unknown parameter ϑ is a realization of a random variable Θ having initial (prior) density u(ϑ). Let

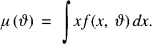
The initial pure premium is

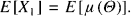
The premium for X t + 1, given X1 +, …, Xt, is the conditional expectation

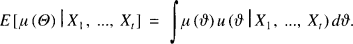
A central question is for which pairs f(x, ϑ) and u (ϑ) this expression is linear, i.e. of the form

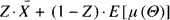
where 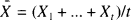is the observed average. This is indeed the case for about half a dozen famous examples. Jewell (1974) has found an elegant and general approach to unify these examples, see also Goovaerts and Hoogstad (1987, chapter 2). The classical examples can be retrieved as special cases; however a preliminary reparameterization has to be performed on a case by case basis. The purpose of this note is to propose an alternative (but of course strongly related) formulation of the general model, from which the classical examples can be retrieved in a straightforward way.