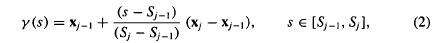Research Article
Bow flows with smooth separation in water of finite depth
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 114-126
-
- Article
-
- You have access
- Export citation
Stability analysis from fourth order evolution equation for small but finite amplitude interfacial waves in the presence of a basic current shear
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 348-365
-
- Article
-
- You have access
- Export citation
On a family of logarithmic and exponential integrals occurring in probability and reliability theory
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 469-478
-
- Article
-
- You have access
- Export citation
Numerical studies on 2-dimensional reaction-diffusion equations
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 223-243
-
- Article
-
- You have access
- Export citation
A numerical scheme for the electromagnetic response in thin conductors of arbitrary planar shape
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 479-497
-
- Article
-
- You have access
- Export citation
A line element algorithm for curve flow problems in the plane
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 244-261
-
- Article
-
- You have access
- Export citation
Front matter
ANZ volume 35 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Pulsatile flow in circular tubes of varying cross-section with suction/injection
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 366-381
-
- Article
-
- You have access
- Export citation
Solution of the problem of scattering of water waves by a nearly vertical plate
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 382-395
-
- Article
-
- You have access
- Export citation
Front matter
ANZ volume 35 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
ANZ volume 35 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
Cost-time trade-off in three-axial sums' transportation problem
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 498-505
-
- Article
-
- You have access
- Export citation
Erratum
Piecewise constant collocation for first-kind boundary integral equations
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 396-398
-
- Article
-
- You have access
- Export citation
Research Article
A boundary value problem of elastoplastic deformation process theory: Existence and uniqueness theorems
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 506-524
-
- Article
-
- You have access
- Export citation
Back matter
ANZ volume 35 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front matter
ANZ volume 35 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
ANZ volume 35 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
ANZ volume 35 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
ANZ volume 35 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

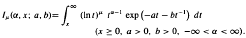
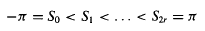

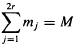 . Then γ(
. Then γ(