We wish to correct a minor error in the recent paper [2]. That paper was concerned with an integral equation defined on a closed polygon Γ with r corners at the points x0, x2, …, x2r = x0. We parameterized Γ using a mapping γ:[−π,π] → Γ defined as follows. For each l, introduce the mid-point x2l−1 of the side joining x2l—2 to x2l. Then introduce 2r + 1 points in parameter space

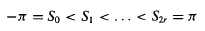
with the property that for each j = 1, …, 2r

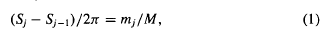
where mj are integers and 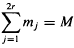. Then γ(s) is defined by

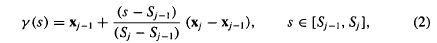
for j = 1, …, 2r. The {Sj} are then the preimages of the {xj} under γ. Moreover, in view of (1), a family of uniform meshes can be constructed on [−π, π] which include {Sj} as the break-points. Then γ maps these to meshes which are uniform on each segment joining xj−1 to xj (which we denote Γj). These meshes are used to discretize the integral equation.