This journal utilises an Online Peer Review Service (OPRS) for submissions. By clicking "Continue" you will be taken to our partner site https://mc.manuscriptcentral.com/apjournals. Please be aware that your Cambridge account is not valid for this OPRS and registration is required. We strongly advise you to read all "Author instructions" in the "Journal information" area prior to submitting.
Extreme value theory concerns the probabilities of extreme and rare events. An important example is the asymptotic behaviour of the maxima of increasing collections of random variables. The classical situation of i.i.d. random variables is studied in the famous Fisher-Tippett-Gnedenko theorem, but one can also consider dependent random variables or take the maxima of collections of random vectors or stochastic processes. Further problems include tail probabilities and the behaviour of a random vector or stochastic process conditioned on some quantity being large. Regular variation and related concepts play a key role in extreme value theory. Extremes are also investigated in other branches of probability theory such as random graphs or stochastic geometry. Extreme value theory is applied in diverse fields ranging from meteorology and environmental science over life sciences to finance and insurance, where, for example, one is interested in modelling risks or computing ruin probabilities.
Collection created by Matthias Schulte (Hamburg University of Technology)
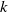 $k$
th-nearest neighbor balls
$k$
th-nearest neighbor balls