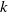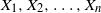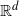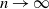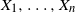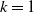1. Introduction and main results
The starting point of this paper is the following result; see [Reference Györfi, Henze and Walk11]. Let
![]() $X,X_1,\ldots,X_n, \ldots $
be a sequence of independent and identically distributed (i.i.d.) random points in
$X,X_1,\ldots,X_n, \ldots $
be a sequence of independent and identically distributed (i.i.d.) random points in
![]() $\mathbb{R}^d$
,
$\mathbb{R}^d$
,
![]() $d\geq 2$
, that are defined on a common probability space
$d\geq 2$
, that are defined on a common probability space
![]() $(\Omega,{\mathcal{A}},\mathbb{P})$
. We assume that the distribution of X, which is denoted by
$(\Omega,{\mathcal{A}},\mathbb{P})$
. We assume that the distribution of X, which is denoted by
![]() $\mu$
, is absolutely continuous with respect to Lebesgue measure
$\mu$
, is absolutely continuous with respect to Lebesgue measure
![]() $\lambda$
, and we denote the density of
$\lambda$
, and we denote the density of
![]() $\mu$
by f. Writing
$\mu$
by f. Writing
![]() $\|\cdot \|$
for the Euclidean norm in
$\|\cdot \|$
for the Euclidean norm in
![]() $\mathbb{R}^d$
, and putting
$\mathbb{R}^d$
, and putting
![]() ${\mathcal{X}}_n \,:\!=\, \{X_1,\ldots,X_n\}$
, let
${\mathcal{X}}_n \,:\!=\, \{X_1,\ldots,X_n\}$
, let
![]() $R_{i,n}\,:\!=\, \min_{j\ne i, j\le n} \|X_i-X_j\|$
be the distance from
$R_{i,n}\,:\!=\, \min_{j\ne i, j\le n} \|X_i-X_j\|$
be the distance from
![]() $X_i$
to its nearest neighbor in the set
$X_i$
to its nearest neighbor in the set
![]() ${\mathcal{X}}_n \setminus \{X_i\}$
. Moreover, let
${\mathcal{X}}_n \setminus \{X_i\}$
. Moreover, let
![]() $1\!\!1 \{A\}$
denote the indicator function of a set A, and write
$1\!\!1 \{A\}$
denote the indicator function of a set A, and write
![]() $B(x,r) = \{y \in \mathbb{R}^d\,:\, \|x-y\|\le r\}$
for the closed ball centered at x with radius r. Finally, let
$B(x,r) = \{y \in \mathbb{R}^d\,:\, \|x-y\|\le r\}$
for the closed ball centered at x with radius r. Finally, let
denote the number of exceedances of probability volumes of nearest neighbor balls that are larger than the threshold
![]() $(t + \log n)/n$
. The main result of [Reference Györfi, Henze and Walk11] is Theorem 2.2 of that paper, which states that, under a weak condition on the density f, for each fixed
$(t + \log n)/n$
. The main result of [Reference Györfi, Henze and Walk11] is Theorem 2.2 of that paper, which states that, under a weak condition on the density f, for each fixed
![]() $t \in \mathbb{R}$
, we have
$t \in \mathbb{R}$
, we have
as
![]() $n \to \infty$
, where
$n \to \infty$
, where
![]() $\overset{\mathcal{D}}{\longrightarrow}$
denotes convergence in distribution, and
$\overset{\mathcal{D}}{\longrightarrow}$
denotes convergence in distribution, and
![]() $\mathrm{Po}(\xi)$
is the Poisson distribution with parameter
$\mathrm{Po}(\xi)$
is the Poisson distribution with parameter
![]() $\xi >0$
.
$\xi >0$
.
Since the maximum probability content of these nearest balls, denoted by
![]() $P_n$
, is at most
$P_n$
, is at most
![]() $(t+ \log n)/n$
if and only if
$(t+ \log n)/n$
if and only if
![]() $C_n =0$
, we immediately obtain a Gumbel limit
$C_n =0$
, we immediately obtain a Gumbel limit
![]() $\lim_{n\to \infty} \mathbb{P}(nP_n - \log n \le t) = \exp\!({-}\exp\!({-}t))$
for
$\lim_{n\to \infty} \mathbb{P}(nP_n - \log n \le t) = \exp\!({-}\exp\!({-}t))$
for
![]() $P_n$
.
$P_n$
.
To state a sufficient condition on f that guarantees (1), let
![]() $\mathrm{supp}(\mu) \,:\!= \{x \in \mathbb{R}^d\,: \mu (B(x,r)) > 0$
for each
$\mathrm{supp}(\mu) \,:\!= \{x \in \mathbb{R}^d\,: \mu (B(x,r)) > 0$
for each
![]() $r >0\}$
denote the support of
$r >0\}$
denote the support of
![]() $\mu$
. Theorem 2.2 of [Reference Györfi, Henze and Walk11] requires that there are
$\mu$
. Theorem 2.2 of [Reference Györfi, Henze and Walk11] requires that there are
![]() $\beta \in (0, 1)$
,
$\beta \in (0, 1)$
,
![]() $c_{\max}<\infty$
and
$c_{\max}<\infty$
and
![]() $\delta >0$
such that, for any
$\delta >0$
such that, for any
![]() $r,s >0$
and any
$r,s >0$
and any
![]() $x,z \in$
$x,z \in$
![]() $\mathrm{supp}(\mu)$
with
$\mathrm{supp}(\mu)$
with
![]() $\|x-z\| \ge \max\{r,s\}$
and
$\|x-z\| \ge \max\{r,s\}$
and
![]() $\mu( B(x,r)) = \mu( B(z,s))\le \delta$
,
$\mu( B(x,r)) = \mu( B(z,s))\le \delta$
,
and
![]() $\mu( B(z, 2s))\le c_{\max}\mu( B(z,s))$
.
$\mu( B(z, 2s))\le c_{\max}\mu( B(z,s))$
.
These conditions hold if
![]() $\mathrm{supp}(\,f)$
is a compact set K (say), and there are
$\mathrm{supp}(\,f)$
is a compact set K (say), and there are
![]() $f_-,f_+ \in (0,\infty)$
such that
$f_-,f_+ \in (0,\infty)$
such that
Thus the density f of X is bounded and bounded away from zero.
The purpose of this paper is to generalize (1) to kth-nearest neighbors, and to derive a rate of convergence for the Poisson approximation of the number of exceedances.
Before stating our main results, we give some more notation. For fixed
![]() $k \le n-1$
, we let
$k \le n-1$
, we let
![]() $R_{i,n,k}$
denote the Euclidean distance of
$R_{i,n,k}$
denote the Euclidean distance of
![]() $X_i$
to its kth-nearest neighbor among
$X_i$
to its kth-nearest neighbor among
![]() ${\mathcal{X}}_n \setminus \{X_i\}$
, and we write
${\mathcal{X}}_n \setminus \{X_i\}$
, and we write
![]() $B(X_i,R_{i,n,k})$
for the kth-nearest neighbor ball centered at
$B(X_i,R_{i,n,k})$
for the kth-nearest neighbor ball centered at
![]() $X_i$
with radius
$X_i$
with radius
![]() $R_{i,n,k}$
. For fixed
$R_{i,n,k}$
. For fixed
![]() $t \in \mathbb{R}$
, put
$t \in \mathbb{R}$
, put
and let
denote the number of exceedances of probability contents of kth-nearest neighbor balls over the threshold
![]() $v_{n,k}$
defined in (3).
$v_{n,k}$
defined in (3).
The term
![]() $\log \log n$
, which shows up in the case
$\log \log n$
, which shows up in the case
![]() $k>1$
, is typical in extreme value theory. It occurs, for example, in the affine transformation of the maximum of n i.i.d. standard normal random variables, which has a Gumbel limit distribution (see Example 3.3.29 of [Reference Embrechts, Klüppelberg and Mikosch10]), or in a recent Poisson limit theorem for the number of cells having at most
$k>1$
, is typical in extreme value theory. It occurs, for example, in the affine transformation of the maximum of n i.i.d. standard normal random variables, which has a Gumbel limit distribution (see Example 3.3.29 of [Reference Embrechts, Klüppelberg and Mikosch10]), or in a recent Poisson limit theorem for the number of cells having at most
![]() $k-1$
particles in the coupon collector’s problem (see Theorem 1 of [Reference Schilling and Henze19]).
$k-1$
particles in the coupon collector’s problem (see Theorem 1 of [Reference Schilling and Henze19]).
The threshold
![]() $v_{n,k}$
is in some sense universal in dealing with the number of exceedances of probability contents of kth-nearest neighbor balls. To this end, suppose that, in much more generality than considered so far,
$v_{n,k}$
is in some sense universal in dealing with the number of exceedances of probability contents of kth-nearest neighbor balls. To this end, suppose that, in much more generality than considered so far,
![]() $X,X_1,X_2, \ldots $
are i.i.d. random elements taking values in a separable metric space
$X,X_1,X_2, \ldots $
are i.i.d. random elements taking values in a separable metric space
![]() $(S,\rho)$
. We retain the notation
$(S,\rho)$
. We retain the notation
![]() $\mu$
for the distribution of X and
$\mu$
for the distribution of X and
![]() $B(x,r) \,:\!=\, \{y \in S\,:\, \rho(x,y) \le r\}$
for the closed ball with radius r centered at
$B(x,r) \,:\!=\, \{y \in S\,:\, \rho(x,y) \le r\}$
for the closed ball with radius r centered at
![]() $x \in S$
. Regarding the distribution
$x \in S$
. Regarding the distribution
![]() $\mu$
, we assume that
$\mu$
, we assume that
As a consequence, the distances
![]() $\rho(X_i,X_j)$
, where
$\rho(X_i,X_j)$
, where
![]() $j \in \{1,\ldots,n\} \setminus \{i\}$
, are different with probability one for each
$j \in \{1,\ldots,n\} \setminus \{i\}$
, are different with probability one for each
![]() $i \in \{1,\ldots,n\}$
. Thus, for fixed
$i \in \{1,\ldots,n\}$
. Thus, for fixed
![]() $k \le n-1$
, there is almost surely a unique kth-nearest neighbor of
$k \le n-1$
, there is almost surely a unique kth-nearest neighbor of
![]() $X_i$
, and we also retain the notation
$X_i$
, and we also retain the notation
![]() $R_{i,n,k}$
for the distance of
$R_{i,n,k}$
for the distance of
![]() $X_i$
to its kth-nearest neighbor among
$X_i$
to its kth-nearest neighbor among
![]() ${\mathcal{X}}_n \setminus \{X_i\}$
and
${\mathcal{X}}_n \setminus \{X_i\}$
and
![]() $B(X_i,R_{i,n,k})$
for the ball centered at
$B(X_i,R_{i,n,k})$
for the ball centered at
![]() $X_i$
with radius
$X_i$
with radius
![]() $R_{i,n,k}$
. Note that condition (5) excludes discrete metric spaces (see e.g. Section 4 of [Reference Zubkov and Orlov20]) but not function spaces such as the space C[0, 1] of continuous functions on [0, 1] with the supremum metric, and with Wiener measure
$R_{i,n,k}$
. Note that condition (5) excludes discrete metric spaces (see e.g. Section 4 of [Reference Zubkov and Orlov20]) but not function spaces such as the space C[0, 1] of continuous functions on [0, 1] with the supremum metric, and with Wiener measure
![]() $\mu$
.
$\mu$
.
In what follows, for sequences
![]() $(a_n)_{n\geq 0}$
and
$(a_n)_{n\geq 0}$
and
![]() $(b_n)_{n\geq 0}$
of real numbers, write
$(b_n)_{n\geq 0}$
of real numbers, write
![]() $a_n={\mathrm{O}}(b_n)$
if
$a_n={\mathrm{O}}(b_n)$
if
![]() $|a_n|\leq C|b_n|$
,
$|a_n|\leq C|b_n|$
,
![]() $n\geq 1$
, for some positive constant C.
$n\geq 1$
, for some positive constant C.
Theorem 1. If
![]() $X_1,X_2, \ldots$
are i.i.d. random elements of a metric space
$X_1,X_2, \ldots$
are i.i.d. random elements of a metric space
![]() $(S,\rho)$
, and if (5) holds, then the sequence
$(S,\rho)$
, and if (5) holds, then the sequence
![]() $(C_{n,k})$
satisfies
$(C_{n,k})$
satisfies
In particular, the mean number of exceedances
![]() $C_{n,k}$
converges to
$C_{n,k}$
converges to
![]() ${\mathrm{e}}^{-t}$
as n goes to infinity. By Markov’s inequality, this result implies the tightness of the sequence
${\mathrm{e}}^{-t}$
as n goes to infinity. By Markov’s inequality, this result implies the tightness of the sequence
![]() $(C_{n,k})_{n \ge 1}$
. Thus at least a subsequence converges in distribution. The next result states convergence of
$(C_{n,k})_{n \ge 1}$
. Thus at least a subsequence converges in distribution. The next result states convergence of
![]() $C_{n,k}$
to a Poisson distribution if
$C_{n,k}$
to a Poisson distribution if
![]() $(S,\rho) = (\mathbb{R}^d,\|\cdot\|)$
and (2) holds. To this end, let
$(S,\rho) = (\mathbb{R}^d,\|\cdot\|)$
and (2) holds. To this end, let
![]() $d_{\mathrm{TV}}(Y,Z)$
be the total variation between two integer-valued random variables Y and Z, that is,
$d_{\mathrm{TV}}(Y,Z)$
be the total variation between two integer-valued random variables Y and Z, that is,
Theorem 2. Let Z be a Poisson random variable with parameter
![]() ${\mathrm{e}}^{-t}$
. If
${\mathrm{e}}^{-t}$
. If
![]() $X, X_1,X_2, \ldots $
are i.i.d. in
$X, X_1,X_2, \ldots $
are i.i.d. in
![]() $\mathbb{R}^d$
with density f, and if the distribution
$\mathbb{R}^d$
with density f, and if the distribution
![]() $\mu$
of X has compact support
$\mu$
of X has compact support
![]() $[0, 1]^d$
and satisfies (2), then, as
$[0, 1]^d$
and satisfies (2), then, as
![]() $n \to \infty$
,
$n \to \infty$
,
Theorem 2 is not only a generalization of Theorem 2.2 of [Reference Györfi, Henze and Walk11] over all
![]() $k\geq 1$
: it also provides a rate of convergence for the Poisson approximation of
$k\geq 1$
: it also provides a rate of convergence for the Poisson approximation of
![]() $C_{n,k}$
. Our theorem is stated in the particular case that the support of
$C_{n,k}$
. Our theorem is stated in the particular case that the support of
![]() $\mu$
is
$\mu$
is
![]() $[0, 1]^d$
, but we think it can be extended to any measure
$[0, 1]^d$
, but we think it can be extended to any measure
![]() $\mu$
whose support is a general convex body. For the sake of readability of the manuscript, we have not dealt with such a generalization.
$\mu$
whose support is a general convex body. For the sake of readability of the manuscript, we have not dealt with such a generalization.
Remark 1. The study of extremes of kth-nearest neighbor balls is classical in stochastic geometry, and it has various applications; see e.g. [Reference Penrose17]. In Section 4 of [Reference Otto16], Otto obtained bounds for the total variation distance of the process of Poisson points with large kth-nearest neighbor ball (with respect to the intensity measure) and a Poisson process. Parallel to our work, Bobrowski et al. have extended these results to the Kantorovich–Rubinstein distance and generalized them to the binomial process, in a paper that has just been submitted [Reference Bobrowski, Schulte and Yogeshwaran5, Section 6.2]. Theorem 6.5 of [Reference Bobrowski, Schulte and Yogeshwaran5] implies our Theorem 2. Nevertheless, the approaches in [Reference Bobrowski, Schulte and Yogeshwaran5, Reference Otto16] and in the present paper are conceptionally different. While the results in [Reference Bobrowski, Schulte and Yogeshwaran5] and [Reference Otto16] rely on Palm couplings of a thinned Poisson/binomial process and employ distances of point processes, we derive a bound on the total variation distance of the number of large kth-nearest neighbor balls and a Poisson-distributed random variable. Our approach permits us to build arguments on classical Poisson approximation theory [Reference Arratia, Goldstein and Gordon2] and an asymptotic independence property stated in Lemma 1 below, and it thus results in a considerably shorter and less technical proof.
Remark 2. From Theorem 2 we can deduce an analogous Poisson approximation result for Poisson input (instead of
![]() $X_1,X_2,\dots$
). Assume without loss of generality that
$X_1,X_2,\dots$
). Assume without loss of generality that
![]() $\mu (\mathbb{R}^d)=1$
, and let
$\mu (\mathbb{R}^d)=1$
, and let
![]() $\eta_n$
be a Poisson process with intensity measure
$\eta_n$
be a Poisson process with intensity measure
![]() $n \mu$
. By Proposition 3.8 of [Reference Last and Penrose15], there are i.i.d. random points
$n \mu$
. By Proposition 3.8 of [Reference Last and Penrose15], there are i.i.d. random points
![]() $X_1,X_2,\dots$
in
$X_1,X_2,\dots$
in
![]() $\mathbb{R}^d$
, where
$\mathbb{R}^d$
, where
![]() $X_1$
has the distribution
$X_1$
has the distribution
![]() $\mu$
, and a Poisson random variable N(n) with expectation n that is independent of
$\mu$
, and a Poisson random variable N(n) with expectation n that is independent of
![]() $X_1,X_2,\dots,$
such that
$X_1,X_2,\dots,$
such that
![]() $\eta_n=\sum_{i=1}^{N(n)} \delta_{X_i}$
. Here
$\eta_n=\sum_{i=1}^{N(n)} \delta_{X_i}$
. Here
![]() $\delta_x$
denotes a unit mass at
$\delta_x$
denotes a unit mass at
![]() $x \in \mathbb{R}^d$
. Let
$x \in \mathbb{R}^d$
. Let
 \begin{equation*}D_{n,k} \,:\!=\, \sum_{i=1}^{N(n)} 1\!\!1 \{\mu ( B(X_i,R_{i,N(n),k})) > v_{n,k}\}\end{equation*}
\begin{equation*}D_{n,k} \,:\!=\, \sum_{i=1}^{N(n)} 1\!\!1 \{\mu ( B(X_i,R_{i,N(n),k})) > v_{n,k}\}\end{equation*}
be the number of exceedances of probability contents of kth-nearest neighbor balls over the threshold
![]() $v_{n,k}$
for the process
$v_{n,k}$
for the process
![]() $\eta_n$
. By the triangle inequality, we have
$\eta_n$
. By the triangle inequality, we have
where
![]() $d_{\mathrm{TV}}(D_{n,k}, C_{n,k})$
is at most
$d_{\mathrm{TV}}(D_{n,k}, C_{n,k})$
is at most
 \begin{align*}\mathbb{E} \Biggl|\sum_{i=1}^{N(n)} 1\!\!1 \{\mu ( B(X_i,R_{i,N(n),k})) > v_{n,k}\}-\sum_{i=1}^n 1\!\!1 \{\mu ( B(X_i,R_{i,n,k})) > v_{n,k}\}\Biggr|.\end{align*}
\begin{align*}\mathbb{E} \Biggl|\sum_{i=1}^{N(n)} 1\!\!1 \{\mu ( B(X_i,R_{i,N(n),k})) > v_{n,k}\}-\sum_{i=1}^n 1\!\!1 \{\mu ( B(X_i,R_{i,n,k})) > v_{n,k}\}\Biggr|.\end{align*}
The last term can be bounded using a concentration inequality for the Poisson distribution; see e.g. Lemma 1.4 of [Reference Penrose18] (we omit the details). Together with Theorem 2, it follows that
as
![]() $n \to \infty$
. This result is also implied by Theorem 4.2 of [Reference Otto16] and by Theorem 6.4 of [Reference Bobrowski, Schulte and Yogeshwaran5].
$n \to \infty$
. This result is also implied by Theorem 4.2 of [Reference Otto16] and by Theorem 6.4 of [Reference Bobrowski, Schulte and Yogeshwaran5].
Now let
![]() $P_{n,k} = \max_{1 \le i \le n} \mu(B(X_i,R_{i,n,k}))$
be the maximum probability content of the kth-nearest neighbor balls. Since
$P_{n,k} = \max_{1 \le i \le n} \mu(B(X_i,R_{i,n,k}))$
be the maximum probability content of the kth-nearest neighbor balls. Since
![]() $C_{n,k} = 0$
if and only if
$C_{n,k} = 0$
if and only if
![]() $P_{n,k} \le v_{n,k}$
, we obtain the following corollary.
$P_{n,k} \le v_{n,k}$
, we obtain the following corollary.
Corollary 1. Under the conditions of Theorem 2, we have
where
![]() ${\rm G}(t) = \exp\!({-}\exp\!({-}t))$
is the distribution function of the Gumbel distribution.
${\rm G}(t) = \exp\!({-}\exp\!({-}t))$
is the distribution function of the Gumbel distribution.
Remark 3. If, in the Euclidean case, the density f is continuous, then
![]() $\mu(B(X_i,R_{i,n,k}))$
is approximately equal to
$\mu(B(X_i,R_{i,n,k}))$
is approximately equal to
![]() $f(X_i)\kappa_d R_{i,n,k}^d$
, where
$f(X_i)\kappa_d R_{i,n,k}^d$
, where
![]() $\kappa_d = \pi^{d/2}/\Gamma(1+d/2)$
is the volume of the unit ball in
$\kappa_d = \pi^{d/2}/\Gamma(1+d/2)$
is the volume of the unit ball in
![]() $\mathbb{R}^d$
. Under additional smoothness assumptions on f and (2), Henze [Reference Henze12, Reference Henze13] proved that
$\mathbb{R}^d$
. Under additional smoothness assumptions on f and (2), Henze [Reference Henze12, Reference Henze13] proved that
where K is the support of
![]() $\mu$
. Here the distance
$\mu$
. Here the distance
![]() $\|X_i-\partial K\|$
of
$\|X_i-\partial K\|$
of
![]() $X_i$
to the boundary of K is important to overcome edge effects. These effects dominate the asymptotic behavior of the maximum of the kth-nearest neighbor distances if
$X_i$
to the boundary of K is important to overcome edge effects. These effects dominate the asymptotic behavior of the maximum of the kth-nearest neighbor distances if
![]() $k \ge d$
; see [Reference Dette and Henze8, Reference Dette and Henze9]. In fact Henze [Reference Henze12] proved convergence of the factorial moments of
$k \ge d$
; see [Reference Dette and Henze8, Reference Dette and Henze9]. In fact Henze [Reference Henze12] proved convergence of the factorial moments of
to the corresponding factorial moments of a random variable with the Poisson distribution
![]() $\mathrm{Po} ({\mathrm{e}}^{-t})$
and thus, by the method of moments, more than (6), namely
$\mathrm{Po} ({\mathrm{e}}^{-t})$
and thus, by the method of moments, more than (6), namely
![]() $\widetilde{C}_{n,k} \overset{\mathcal{D}}{\rightarrow} \mathrm{Po} ({\mathrm{e}}^{-t})$
. However, our proof of Theorem 2 is completely different, since it is based on the Chen–Stein method and provides a rate of convergence.
$\widetilde{C}_{n,k} \overset{\mathcal{D}}{\rightarrow} \mathrm{Po} ({\mathrm{e}}^{-t})$
. However, our proof of Theorem 2 is completely different, since it is based on the Chen–Stein method and provides a rate of convergence.
2. Proofs
2.1. Proof of Theorem 1
Proof. By symmetry, we have
For a fixed
![]() $x \in S$
, let
$x \in S$
, let
be the cumulative distribution function of
![]() $\rho(x,X)$
. Due to the condition (5), the function
$\rho(x,X)$
. Due to the condition (5), the function
![]() $H_x$
is continuous, and by the probability integral transform (see e.g. [Reference Biau and Devroye4, p. 8]), the random variable
$H_x$
is continuous, and by the probability integral transform (see e.g. [Reference Biau and Devroye4, p. 8]), the random variable
is uniformly distributed in the unit interval [0, 1]. Put
![]() $U_j \,:\!=\, H_x(\rho(x,X_{j+1}))$
,
$U_j \,:\!=\, H_x(\rho(x,X_{j+1}))$
,
![]() $j=1,\ldots,n-1$
. Then
$j=1,\ldots,n-1$
. Then
![]() $U_1,\ldots,U_{n-1}$
are i.i.d. random variables with a uniform distribution in (0, 1). Hence, conditionally on
$U_1,\ldots,U_{n-1}$
are i.i.d. random variables with a uniform distribution in (0, 1). Hence, conditionally on
![]() $X_1=x$
, the random variable
$X_1=x$
, the random variable
![]() $\mu (B(X_1,R_{1,n,k}))$
has the same distribution as
$\mu (B(X_1,R_{1,n,k}))$
has the same distribution as
![]() $U_{k\,:\, n-1}$
, where
$U_{k\,:\, n-1}$
, where
![]() $U_{1\,:\, n-1} < \cdots < U_{n-1\,:\, n-1}$
are the order statistics of
$U_{1\,:\, n-1} < \cdots < U_{n-1\,:\, n-1}$
are the order statistics of
![]() $U_1,\ldots,U_{n-1}$
, and this distribution does not depend on x. Now, because of a well-known relation between the distribution of order statistics from the uniform distribution on (0, 1) and the binomial distribution (see e.g. [Reference Ahsanullah, Nevzzorov and Shakil1, p. 16]), we have
$U_1,\ldots,U_{n-1}$
, and this distribution does not depend on x. Now, because of a well-known relation between the distribution of order statistics from the uniform distribution on (0, 1) and the binomial distribution (see e.g. [Reference Ahsanullah, Nevzzorov and Shakil1, p. 16]), we have
 \begin{equation*}\mathbb{P}(U_{k\,:\, n-1} > s) = \sum_{j=0}^{k-1} \binom{n-1 }{ j} s^j (1-s)^{n-1-j}\end{equation*}
\begin{equation*}\mathbb{P}(U_{k\,:\, n-1} > s) = \sum_{j=0}^{k-1} \binom{n-1 }{ j} s^j (1-s)^{n-1-j}\end{equation*}
and thus
 \begin{equation}\mathbb{E} [C_{n,k}] = n \sum_{j=0}^{k-1} \binom{n-1 }{ j} v_{n,k}^j (1-v_{n,k})^{n-1-j}.\end{equation}
\begin{equation}\mathbb{E} [C_{n,k}] = n \sum_{j=0}^{k-1} \binom{n-1 }{ j} v_{n,k}^j (1-v_{n,k})^{n-1-j}.\end{equation}
Here the summand for
![]() $j=k-1$
equals
$j=k-1$
equals
 \begin{equation*}n \binom{n-1 }{ k-1} v_{n,k}^{k-1} (1-v_{n,k})^{n-k} = \dfrac{n}{(k-1)!}\, (nv_{n,k})^{k-1}\, \prod_{i=1}^{k-1}\dfrac{n-i}{n}\, (1-v_{n,k})^{n-k}.\end{equation*}
\begin{equation*}n \binom{n-1 }{ k-1} v_{n,k}^{k-1} (1-v_{n,k})^{n-k} = \dfrac{n}{(k-1)!}\, (nv_{n,k})^{k-1}\, \prod_{i=1}^{k-1}\dfrac{n-i}{n}\, (1-v_{n,k})^{n-k}.\end{equation*}
Using Taylor expansions, (3) yields
 \begin{equation*}nv_{n,k} = \log n+{\mathrm{O}} (\!\log\log n), \quad \prod_{i=1}^{k-1}\dfrac{n-i}{n} = 1+{\mathrm{O}}\biggl( \dfrac{1}{n}\biggr) \end{equation*}
\begin{equation*}nv_{n,k} = \log n+{\mathrm{O}} (\!\log\log n), \quad \prod_{i=1}^{k-1}\dfrac{n-i}{n} = 1+{\mathrm{O}}\biggl( \dfrac{1}{n}\biggr) \end{equation*}
and
Straightforward computations now give
Regarding the remaining summands on the right-hand side of (7), it is readily seen that
 \begin{equation*}\sum_{j=0}^{k-2} \binom{n-1 }{ j} v_{n,k}^j (1-v_{n,k})^{n-1-j} = {\mathrm{O}}\biggl( n \binom{n-1 }{ k-1} v_{n,k}^{k-1} (1-v_{n,k})^{n-k} \cdot \dfrac{1}{nv_{n,k}} \biggr),\end{equation*}
\begin{equation*}\sum_{j=0}^{k-2} \binom{n-1 }{ j} v_{n,k}^j (1-v_{n,k})^{n-1-j} = {\mathrm{O}}\biggl( n \binom{n-1 }{ k-1} v_{n,k}^{k-1} (1-v_{n,k})^{n-k} \cdot \dfrac{1}{nv_{n,k}} \biggr),\end{equation*}
with the convention that the sum equals 0 if
![]() $k=1$
. From the above computations and from (3), it follows that this sum equals
$k=1$
. From the above computations and from (3), it follows that this sum equals
![]() ${\mathrm{O}}(1/\log n )$
, which concludes the proof of Theorem 1.
${\mathrm{O}}(1/\log n )$
, which concludes the proof of Theorem 1.
Remark 4. In the proof given above, we conditioned on the realizations x of
![]() $X_1$
. Since the distribution of
$X_1$
. Since the distribution of
![]() $H_x(\rho(x,X)) = \mu(B(x,\rho(x,X)))$
does not depend on X, we obtain as a by-product that
$H_x(\rho(x,X)) = \mu(B(x,\rho(x,X)))$
does not depend on X, we obtain as a by-product that
 \begin{equation*}\mathbb{P}(\mu (B(X_1,R_{1,n,k})) > v_{n,k} ) = \sum_{j=0}^{k-1} \binom{n-1 }{ j} v_{n,k}^j (1-v_{n,k})^{n-1-j} \sim \dfrac{{\mathrm{e}}^{-t}}{n},\end{equation*}
\begin{equation*}\mathbb{P}(\mu (B(X_1,R_{1,n,k})) > v_{n,k} ) = \sum_{j=0}^{k-1} \binom{n-1 }{ j} v_{n,k}^j (1-v_{n,k})^{n-1-j} \sim \dfrac{{\mathrm{e}}^{-t}}{n},\end{equation*}
if
![]() $X_1,X_2,\ldots,X_n$
are independent and
$X_1,X_2,\ldots,X_n$
are independent and
![]() $X_2,\ldots,X_n$
are i.i.d. according to
$X_2,\ldots,X_n$
are i.i.d. according to
![]() $\mu$
. Here
$\mu$
. Here
![]() $X_1$
may have an arbitrary distribution and
$X_1$
may have an arbitrary distribution and
![]() $a_n \sim b_n$
means that
$a_n \sim b_n$
means that
![]() $a_n/b_n \to 1$
as
$a_n/b_n \to 1$
as
![]() $n \to \infty$
.
$n \to \infty$
.
2.2. Proof of Theorem 2
The main idea to derive Theorem 2 is to discretize
![]() $\mathrm{supp}(\mu)=[0, 1]^d$
into finitely many ‘small sets’ and then to employ the Chen–Stein method. To apply this method we will have to check an asymptotic independence property and a local property which ensures that, with high probability, two exceedances cannot appear in the same neighborhood. We introduce these properties below and recall a result due to Arratia et al. [Reference Arratia, Goldstein and Gordon2] on the Chen–Stein method.
$\mathrm{supp}(\mu)=[0, 1]^d$
into finitely many ‘small sets’ and then to employ the Chen–Stein method. To apply this method we will have to check an asymptotic independence property and a local property which ensures that, with high probability, two exceedances cannot appear in the same neighborhood. We introduce these properties below and recall a result due to Arratia et al. [Reference Arratia, Goldstein and Gordon2] on the Chen–Stein method.
2.2.1. The asymptotic independence property
Fix
![]() $\varepsilon > 0$
. Writing
$\varepsilon > 0$
. Writing
![]() $\lfloor \cdot \rfloor$
for the floor function, we partition
$\lfloor \cdot \rfloor$
for the floor function, we partition
![]() $[0, 1]^d$
into a set
$[0, 1]^d$
into a set
![]() $\mathcal{V}_n$
of
$\mathcal{V}_n$
of
![]() $N_n^d$
subcubes (i.e. subsets that are cubes) of equal size that can only have boundary points in common, where
$N_n^d$
subcubes (i.e. subsets that are cubes) of equal size that can only have boundary points in common, where
The subcubes are indexed by the set
With a slight abuse of notation, we identify a cube with its index. Let
be the event that each of the subcubes contains at least one of the points of
![]() ${\mathcal{X}}_n$
. The event
${\mathcal{X}}_n$
. The event
![]() $\mathcal{E}_n$
is extensively used in stochastic geometry to derive central limit theorems or to deal with extremes [Reference Avram and Bertsimas3, Reference Bonnet and Chenavier6, Reference Chenavier and Robert7], and it will play a crucial role throughout the rest of the paper. The following lemma, which captures the idea of ‘asymptotic independence’, is at the heart of our development.
$\mathcal{E}_n$
is extensively used in stochastic geometry to derive central limit theorems or to deal with extremes [Reference Avram and Bertsimas3, Reference Bonnet and Chenavier6, Reference Chenavier and Robert7], and it will play a crucial role throughout the rest of the paper. The following lemma, which captures the idea of ‘asymptotic independence’, is at the heart of our development.
Lemma 1. For each
![]() $\alpha>0$
, we have
$\alpha>0$
, we have
![]() $\operatorname{\mathbb{P}}\!({\mathcal{E}_n^c})={\mathrm{o}}(n^{-\alpha})$
as
$\operatorname{\mathbb{P}}\!({\mathcal{E}_n^c})={\mathrm{o}}(n^{-\alpha})$
as
![]() $n \to \infty$
.
$n \to \infty$
.
Proof. By subadditivity and independence, it follows that
 \begin{align*}\operatorname{\mathbb{P}}\!({\mathcal{E}_n^c}) & \leq \sum_{\textbf{j}\in \mathcal{V}_n}\operatorname{\mathbb{P}}\!({{\mathcal{X}}_n\cap \textbf{j}=\emptyset})\\& = \sum_{\textbf{j}\in \mathcal{V}_n}(\!\operatorname{\mathbb{P}}\!({X_1\not\in \textbf{j}}) )^n\\& = \sum_{\textbf{j}\in \mathcal{V}_n} (1-\mu(\textbf{j}))^n\\& \leq \sum_{\textbf{j}\in \mathcal{V}_n} \exp\!({-}n\mu(\textbf{j})).\end{align*}
\begin{align*}\operatorname{\mathbb{P}}\!({\mathcal{E}_n^c}) & \leq \sum_{\textbf{j}\in \mathcal{V}_n}\operatorname{\mathbb{P}}\!({{\mathcal{X}}_n\cap \textbf{j}=\emptyset})\\& = \sum_{\textbf{j}\in \mathcal{V}_n}(\!\operatorname{\mathbb{P}}\!({X_1\not\in \textbf{j}}) )^n\\& = \sum_{\textbf{j}\in \mathcal{V}_n} (1-\mu(\textbf{j}))^n\\& \leq \sum_{\textbf{j}\in \mathcal{V}_n} \exp\!({-}n\mu(\textbf{j})).\end{align*}
Here the last inequality holds since
![]() $\log\!(1-x)\leq -x$
for each
$\log\!(1-x)\leq -x$
for each
![]() $x\in [0, 1)$
. Since
$x\in [0, 1)$
. Since
![]() $f\geq f_- >0$
on K, we have
$f\geq f_- >0$
on K, we have
![]() $\mu(\textbf{j})=\int_\textbf{j} f \,{\mathrm{d}} \lambda \geq f_- \lambda(\textbf{j})$
, whence, writing
$\mu(\textbf{j})=\int_\textbf{j} f \,{\mathrm{d}} \lambda \geq f_- \lambda(\textbf{j})$
, whence, writing
![]() $\# M$
for the cardinality of a finite set M,
$\# M$
for the cardinality of a finite set M,
 \begin{align*}\mathbb{P} (\mathcal{E}_n^c) & \leq \sum_{\textbf{j}\in \mathcal{V}_n} \exp\!({-}n f_- \lambda(\textbf{j}))\\&\leq \#\mathcal{V}_n \exp\bigl({-} f_-(\!\log n)^{1+\varepsilon}\bigr).\end{align*}
\begin{align*}\mathbb{P} (\mathcal{E}_n^c) & \leq \sum_{\textbf{j}\in \mathcal{V}_n} \exp\!({-}n f_- \lambda(\textbf{j}))\\&\leq \#\mathcal{V}_n \exp\bigl({-} f_-(\!\log n)^{1+\varepsilon}\bigr).\end{align*}
Since
![]() $\#\mathcal{V}_n\leq n/(\!\log n)^{1+\varepsilon}$
, it follows that
$\#\mathcal{V}_n\leq n/(\!\log n)^{1+\varepsilon}$
, it follows that
![]() $n^\alpha \operatorname{\mathbb{P}}\!({\mathcal{E}_n^c}) \to 0 \text{ as } n \to \infty$
.
$n^\alpha \operatorname{\mathbb{P}}\!({\mathcal{E}_n^c}) \to 0 \text{ as } n \to \infty$
.
2.2.2. The local property
Now define a metric
![]() $\texttt{d}$
on
$\texttt{d}$
on
![]() $\mathcal{V}_n$
by putting
$\mathcal{V}_n$
by putting
![]() $\texttt{d}(\textbf{j},\textbf{j}^{\prime})\,:\!=\, \max_{1\leq s\leq d}|j_{s}-j^{\prime}_{s}|$
for any two different subcubes
$\texttt{d}(\textbf{j},\textbf{j}^{\prime})\,:\!=\, \max_{1\leq s\leq d}|j_{s}-j^{\prime}_{s}|$
for any two different subcubes
![]() $\textbf{j}$
and
$\textbf{j}$
and
![]() $\textbf{j}^{\prime}$
, and
$\textbf{j}^{\prime}$
, and
![]() $\texttt{d}(\textbf{j},\textbf{j})\,:\!=\, 0$
,
$\texttt{d}(\textbf{j},\textbf{j})\,:\!=\, 0$
,
![]() $\textbf{j} \in \mathcal{V}_n$
. Let
$\textbf{j} \in \mathcal{V}_n$
. Let
be the ball of subcubes of radius r centered at
![]() $\textbf{j}$
. For any
$\textbf{j}$
. For any
![]() $\textbf{j}\in \mathcal{V}_n$
, put
$\textbf{j}\in \mathcal{V}_n$
, put
with the convention
![]() $M_\textbf{j}=0$
if
$M_\textbf{j}=0$
if
![]() ${\mathcal{X}}_n\cap \textbf{j}=\emptyset$
. Conditionally on the event
${\mathcal{X}}_n\cap \textbf{j}=\emptyset$
. Conditionally on the event
![]() $\mathcal{E}_n$
, and provided that
$\mathcal{E}_n$
, and provided that
![]() $\texttt{d}(\textbf{j},\textbf{j}^{\prime})\geq 2k+1$
, the random variables
$\texttt{d}(\textbf{j},\textbf{j}^{\prime})\geq 2k+1$
, the random variables
![]() $M_\textbf{j}$
and
$M_\textbf{j}$
and
![]() $M_{\textbf{j}^{\prime}}$
are independent. Lemma 1 is referred to as the asymptotic independence property: conditionally on the event
$M_{\textbf{j}^{\prime}}$
are independent. Lemma 1 is referred to as the asymptotic independence property: conditionally on the event
![]() $\mathcal{E}_n$
, which occurs with high probability, the extremes
$\mathcal{E}_n$
, which occurs with high probability, the extremes
![]() $M_\textbf{j}$
and
$M_\textbf{j}$
and
![]() $M^{\prime}_\textbf{j}$
attained on two subcubes which are sufficiently distant from each other are independent.
$M^{\prime}_\textbf{j}$
attained on two subcubes which are sufficiently distant from each other are independent.
The following lemma claims that, with high probability, two exceedances cannot occur in the same neighborhood.
Lemma 2. With the notation
![]() $a \wedge b \,:\!=\, \min(a,b)$
for
$a \wedge b \,:\!=\, \min(a,b)$
for
![]() $a,b \in \mathbb{R}$
, let
$a,b \in \mathbb{R}$
, let
Then
![]() $R(n) = {\mathrm{O}}\bigl(n^{-1}(\!\log n)^{2-d+\varepsilon}\bigr)$
as
$R(n) = {\mathrm{O}}\bigl(n^{-1}(\!\log n)^{2-d+\varepsilon}\bigr)$
as
![]() $n \to \infty$
.
$n \to \infty$
.
Here, with a slight abuse of notation, we have identified the family of subcubes
![]() $S(\textbf{j},2k)=\{\textbf{j}^{\prime}\in \mathcal{V}_n\,:\, {\texttt{d}} (\textbf{j},\textbf{j}^{\prime})\leq 2k\}$
with the set
$S(\textbf{j},2k)=\{\textbf{j}^{\prime}\in \mathcal{V}_n\,:\, {\texttt{d}} (\textbf{j},\textbf{j}^{\prime})\leq 2k\}$
with the set
![]() $\bigcup \big\{\textbf{j}^{\prime}\,:\, \textbf{j}^{\prime}\in \mathcal{V}_n \text{ and } {\texttt{d}} (\textbf{j},\textbf{j}^{\prime})\leq 2k\}.$
$\bigcup \big\{\textbf{j}^{\prime}\,:\, \textbf{j}^{\prime}\in \mathcal{V}_n \text{ and } {\texttt{d}} (\textbf{j},\textbf{j}^{\prime})\leq 2k\}.$
We prepare the proof of Lemma 2. with the following result, which gives the volume of two d-dimensional balls.
Lemma 3. If
![]() $x \in B(0,2)$
, then
$x \in B(0,2)$
, then
Proof. We calculate the volume of
![]() $\lambda(B(0, 1)\cup B(x,1))$
as the sum of the volumes of the following two congruent sets. The first one, say B, is given by the set of all points in
$\lambda(B(0, 1)\cup B(x,1))$
as the sum of the volumes of the following two congruent sets. The first one, say B, is given by the set of all points in
![]() $B(0, 1)\cup B(x,1)$
that are closer to 0 than to x, and for the second one we change the roles of 0 and x. The set B is the union of a cone C with radius
$B(0, 1)\cup B(x,1)$
that are closer to 0 than to x, and for the second one we change the roles of 0 and x. The set B is the union of a cone C with radius
![]() $\sqrt{1-(\|x\|/2)^2}$
, height
$\sqrt{1-(\|x\|/2)^2}$
, height
![]() $\|x\|/2$
and apex at the origin and a set
$\|x\|/2$
and apex at the origin and a set
![]() $D\,:\!=\, B(0, 1)\setminus S$
, where S is a simplicial cone with external angle
$D\,:\!=\, B(0, 1)\setminus S$
, where S is a simplicial cone with external angle
![]() $\arccos\!(\|x\|/2)$
. From elementary geometry, we obtain that the volumes of C and d are given by
$\arccos\!(\|x\|/2)$
. From elementary geometry, we obtain that the volumes of C and d are given by
This finishes the proof of the lemma.
Proof of Lemma
2. For
![]() $z \in {[0, 1]^d}$
, let
$z \in {[0, 1]^d}$
, let
Writing
![]() $\#{\mathcal{Y}}(A)$
for the number of points of a finite set
$\#{\mathcal{Y}}(A)$
for the number of points of a finite set
![]() ${\mathcal{Y}}$
of random points in
${\mathcal{Y}}$
of random points in
![]() $\mathbb{R}^d$
that fall into a Borel set A, we have
$\mathbb{R}^d$
that fall into a Borel set A, we have
In the following, we assume that
![]() $r_{n,k}(X_{i^{\prime}})\le r_{n,k}(X_{i})$
(which is at the cost of a factor 2) and distinguish the two cases
$r_{n,k}(X_{i^{\prime}})\le r_{n,k}(X_{i})$
(which is at the cost of a factor 2) and distinguish the two cases
![]() $X_{i^{\prime}} \in B(X_i,r_{n,k}(X_{i}))$
and
$X_{i^{\prime}} \in B(X_i,r_{n,k}(X_{i}))$
and
![]() $X_{i^{\prime}} \in S(\textbf{j},2k) \setminus B(X_i,r_{n,k}(X_{i}))$
. This distinction of cases gives
$X_{i^{\prime}} \in S(\textbf{j},2k) \setminus B(X_i,r_{n,k}(X_{i}))$
. This distinction of cases gives
 \begin{align*}&\mathbb{P} \bigl( X_i,X_{i^{\prime}}\in S(\textbf{j},2k);\, \mu(B(X_i,R_{i,n,k})) \wedge \mu(B(X_{i^{\prime}},R_{i^{\prime},n,k}))>v_{n,k} \bigr)\notag\\&\quad\le 2 \mathbb{P} \bigl( X_i,X_{i^{\prime}}\in S(\textbf{j},2k);\, r_{n,k}(X_{i^{\prime}})\le r_{n,k}(X_{i}); \notag\\ &\quad \quad \quad \mu(B(X_i,R_{i,n,k})) \wedge \mu(B(X_{i^{\prime}},R_{i^{\prime},n,k}))>v_{n,k} \bigr).\end{align*}
\begin{align*}&\mathbb{P} \bigl( X_i,X_{i^{\prime}}\in S(\textbf{j},2k);\, \mu(B(X_i,R_{i,n,k})) \wedge \mu(B(X_{i^{\prime}},R_{i^{\prime},n,k}))>v_{n,k} \bigr)\notag\\&\quad\le 2 \mathbb{P} \bigl( X_i,X_{i^{\prime}}\in S(\textbf{j},2k);\, r_{n,k}(X_{i^{\prime}})\le r_{n,k}(X_{i}); \notag\\ &\quad \quad \quad \mu(B(X_i,R_{i,n,k})) \wedge \mu(B(X_{i^{\prime}},R_{i^{\prime},n,k}))>v_{n,k} \bigr).\end{align*}
Therefore
 \begin{align} &\mathbb{P} \bigl( X_i,X_{i^{\prime}}\in S(\textbf{j},2k);\, \mu(B(X_i,R_{i,n,k})) \wedge \mu(B(X_{i^{\prime}},R_{i^{\prime},n,k}))>v_{n,k} \bigr)\nonumber\\&\quad \le 2 \mathbb{P} \bigl( X_i \in S(\textbf{j},2k);\, X_{i^{\prime}} \in B(X_i,r_{n,k}(X_{i}));\, r_{n,k}(X_{i^{\prime}})\le r_{n,k}(X_{i});\nonumber\\ &\quad \quad \quad \quad \mu(B(X_i,R_{i,n,k})) \wedge \mu(B(X_{i^{\prime}},R_{i^{\prime},n,k}))>v_{n,k} \bigr)\end{align}
\begin{align} &\mathbb{P} \bigl( X_i,X_{i^{\prime}}\in S(\textbf{j},2k);\, \mu(B(X_i,R_{i,n,k})) \wedge \mu(B(X_{i^{\prime}},R_{i^{\prime},n,k}))>v_{n,k} \bigr)\nonumber\\&\quad \le 2 \mathbb{P} \bigl( X_i \in S(\textbf{j},2k);\, X_{i^{\prime}} \in B(X_i,r_{n,k}(X_{i}));\, r_{n,k}(X_{i^{\prime}})\le r_{n,k}(X_{i});\nonumber\\ &\quad \quad \quad \quad \mu(B(X_i,R_{i,n,k})) \wedge \mu(B(X_{i^{\prime}},R_{i^{\prime},n,k}))>v_{n,k} \bigr)\end{align}
We bound the summands (8) and (9) separately. Since
![]() $X_i$
and
$X_i$
and
![]() $X_{i^{\prime}}$
are independent, (8) takes the form
$X_{i^{\prime}}$
are independent, (8) takes the form
 \begin{align*}&2\int_{S(\textbf{j},2k)} \int_{B(x,r_{n,k}(x))} \, \mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\} \cup \{x\})(B(y,r_{n,k}(y)))\le k-1; \notag\\&\quad \quad \#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\} \cup \{y\})(B(x,r_{n,k}(x)))\le k-1\bigr)\,1\!\!1{\{r_{n,k}(y) \le r_{n,k}(x)\}}\, \mu(\mathrm{d}y)\,\mu(\mathrm{d}x). \end{align*}
\begin{align*}&2\int_{S(\textbf{j},2k)} \int_{B(x,r_{n,k}(x))} \, \mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\} \cup \{x\})(B(y,r_{n,k}(y)))\le k-1; \notag\\&\quad \quad \#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\} \cup \{y\})(B(x,r_{n,k}(x)))\le k-1\bigr)\,1\!\!1{\{r_{n,k}(y) \le r_{n,k}(x)\}}\, \mu(\mathrm{d}y)\,\mu(\mathrm{d}x). \end{align*}
For
![]() $y \in B(x,r_{n,k}(x))$
, the probability in the integrand figuring above is bounded from above by
$y \in B(x,r_{n,k}(x))$
, the probability in the integrand figuring above is bounded from above by
 \begin{align}&\mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(y,r_{n,k}(y)))\le k-1;\notag\\&\quad \quad \#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(x,r_{n,k}(x)))\le k-2\bigr)\notag\\&\quad \le \mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(y,r_{n,k}(y)))\le k-1;\notag\\&\quad \quad \#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(y))\le k-2)\bigr).\end{align}
\begin{align}&\mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(y,r_{n,k}(y)))\le k-1;\notag\\&\quad \quad \#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(x,r_{n,k}(x)))\le k-2\bigr)\notag\\&\quad \le \mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(y,r_{n,k}(y)))\le k-1;\notag\\&\quad \quad \#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(y))\le k-2)\bigr).\end{align}
Since the random vector
is negatively quadrant-dependent (see [Reference Joag-Dev and Proschan14, Section 3.1]), equation (10) has the upper bound
 \begin{align}& \mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(y,r_{n,k}(y)))\le k-1\bigr)\notag\\&\quad\quad \times \mathbb{P}\bigl( \#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(y)))\le k-2\bigr)\notag\\&\quad \le \mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(y,r_{n,k}(y)))\le k-1\bigr)\notag\\&\quad \quad \times \mathbb{P}\bigl( \#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(x)))\le k-2\bigr),\end{align}
\begin{align}& \mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(y,r_{n,k}(y)))\le k-1\bigr)\notag\\&\quad\quad \times \mathbb{P}\bigl( \#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(y)))\le k-2\bigr)\notag\\&\quad \le \mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(y,r_{n,k}(y)))\le k-1\bigr)\notag\\&\quad \quad \times \mathbb{P}\bigl( \#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(x)))\le k-2\bigr),\end{align}
where the last inequality holds since
![]() $r_{n,k}(y) \le r_{n,k}(x)$
. Analogously to Remark 4, the first probability is
$r_{n,k}(y) \le r_{n,k}(x)$
. Analogously to Remark 4, the first probability is
 \begin{align*}\mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(y,r_{n,k}(y)))\le k-1\bigr)= \sum_{j=0}^{k-1} \binom{n-2 }{ j} v_{n,k}^j (1-v_{n,k})^{n-2-j} \sim \dfrac{{\mathrm{e}}^{-t}}{n}.\end{align*}
\begin{align*}\mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(y,r_{n,k}(y)))\le k-1\bigr)= \sum_{j=0}^{k-1} \binom{n-2 }{ j} v_{n,k}^j (1-v_{n,k})^{n-2-j} \sim \dfrac{{\mathrm{e}}^{-t}}{n}.\end{align*}
The latter probability in (11) is given by
 \begin{align}&\sum_{\ell=0}^{k-2} \binom{n-2}{\ell} \mu (B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(x)))^\ell (1-\mu(B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(x))))^{n-2-\ell}.\nonumber\\[-8pt] \end{align}
\begin{align}&\sum_{\ell=0}^{k-2} \binom{n-2}{\ell} \mu (B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(x)))^\ell (1-\mu(B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(x))))^{n-2-\ell}.\nonumber\\[-8pt] \end{align}
In a next step, we estimate
![]() $\mu (B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(x)))$
. Since
$\mu (B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(x)))$
. Since
![]() $f(x) \ge f_- >0,\,x \in {[0, 1]^d}$
, and by the homogeneity of d-dimensional Lebesgue measure
$f(x) \ge f_- >0,\,x \in {[0, 1]^d}$
, and by the homogeneity of d-dimensional Lebesgue measure
![]() $\lambda$
, we obtain
$\lambda$
, we obtain
 \begin{align*}\mu (B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(x)))&\ge\, f_- \lambda (B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(x))) \\& =\, f_- r_{n,k}(x)^d \lambda (B(0, 1)\setminus B(r_{n,k}(x)^{-1}(y-x),1))\\& =\, f_- r_{n,k}(x)^d (\lambda (B(0, 1)\cup B(r_{n,k}(x)^{-1}(y-x),1))-\kappa_d).\end{align*}
\begin{align*}\mu (B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(x)))&\ge\, f_- \lambda (B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(x))) \\& =\, f_- r_{n,k}(x)^d \lambda (B(0, 1)\setminus B(r_{n,k}(x)^{-1}(y-x),1))\\& =\, f_- r_{n,k}(x)^d (\lambda (B(0, 1)\cup B(r_{n,k}(x)^{-1}(y-x),1))-\kappa_d).\end{align*}
For
![]() $y \in B(x,r_{n,k}(x))$
, Lemma 3 yields
$y \in B(x,r_{n,k}(x))$
, Lemma 3 yields
 \begin{align*} & \mu (B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(x))) \ge f_- r_{n,k}(x)^{d}\\ &\quad \times \biggl(\kappa_d\biggl(1-\dfrac{2\arccos\!(\|x-y\|/2r_{n,k}(x))}{\pi}\biggr)+\dfrac{\|x-y\|\kappa_{d-1}}{2dr_{n,k}(x)}\Bigl(\sqrt{1-(\|x-y\|/2r_{n,k}(x))^2}\Bigr)^{d-1}\biggr). \end{align*}
\begin{align*} & \mu (B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(x))) \ge f_- r_{n,k}(x)^{d}\\ &\quad \times \biggl(\kappa_d\biggl(1-\dfrac{2\arccos\!(\|x-y\|/2r_{n,k}(x))}{\pi}\biggr)+\dfrac{\|x-y\|\kappa_{d-1}}{2dr_{n,k}(x)}\Bigl(\sqrt{1-(\|x-y\|/2r_{n,k}(x))^2}\Bigr)^{d-1}\biggr). \end{align*}
Since
![]() $\inf_{s>0} s^{-1}(1-2\arccos\!(s)/\pi)>0$
, there is
$\inf_{s>0} s^{-1}(1-2\arccos\!(s)/\pi)>0$
, there is
![]() $c_0>0$
such that
$c_0>0$
such that
Equation (12) and the bound
![]() $f(x) \le f_+,\,x \in {[0, 1]^d},$
give
$f(x) \le f_+,\,x \in {[0, 1]^d},$
give
 \begin{align*}&\int_{B(x,r_{n,k}(x))} \mathbb{P} \bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(x,r_{n,k}(x))\setminus B(y,r_{n,k}({x})))\le k-1\bigr)\\& \quad \quad \times 1\!\!1{\{r_{n,k}(y) \le r_{n,k}(x)\}}\, \mu(\mathrm{d}y)\\&\quad \le f_+ \sum_{\ell=0}^{k-2} \binom{n-2}{\ell} \int_{B(x,r_{n,k}(x))} \bigl(c_0\|x-y\|r_{n,k}(x)^{d-1}\bigr)^\ell\\& \quad\quad \times \bigl(1-c_0\|x-y\|r_{n,k}(x)^{d-1}\bigr)^{n-2-\ell} \lambda(\mathrm{d}y).\end{align*}
\begin{align*}&\int_{B(x,r_{n,k}(x))} \mathbb{P} \bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(x,r_{n,k}(x))\setminus B(y,r_{n,k}({x})))\le k-1\bigr)\\& \quad \quad \times 1\!\!1{\{r_{n,k}(y) \le r_{n,k}(x)\}}\, \mu(\mathrm{d}y)\\&\quad \le f_+ \sum_{\ell=0}^{k-2} \binom{n-2}{\ell} \int_{B(x,r_{n,k}(x))} \bigl(c_0\|x-y\|r_{n,k}(x)^{d-1}\bigr)^\ell\\& \quad\quad \times \bigl(1-c_0\|x-y\|r_{n,k}(x)^{d-1}\bigr)^{n-2-\ell} \lambda(\mathrm{d}y).\end{align*}
We now introduce spherical coordinates and obtain
 \begin{align*}&f_+ d \kappa_d \sum_{\ell=0}^{k-2} \binom{n-2}{\ell} \int_0^{r_{n,k}(x)} \bigl(c_0 t r_{n,k}(x)^{d-1}\bigr)^\ell \bigl(1-c_0 t r_{n,k}(x)^{d-1}\bigr)^{n-2-\ell} t^{d-1} \mathrm{d}t\\&\quad =f_+ d \kappa_d \sum_{\ell=0}^{k-2} \binom{n-2}{\ell} \int_0^{r_{n,k}(x)} \bigl(c_0 t r_{n,k}(x)^{d-1}\bigr)^\ell\\& \quad\quad \times\exp \bigl( (n-2-\ell) \log\!(1-c_0 t r_{n,k}(x)^{d-1})\bigr) t^{d-1} \mathrm{d}t\\&\quad \le f_+d \kappa_d \sum_{\ell=0}^{k-2} \binom{n-2}{\ell} \int_0^{r_{n,k}(x)} \bigl(c_0 t r_{n,k}(x)^{d-1}\bigr)^\ell\\& \quad\quad \times \exp \bigl( -c_0(n-2-\ell) t r_{n,k}(x)^{d-1}\bigr) t^{d-1} \mathrm{d}t.\end{align*}
\begin{align*}&f_+ d \kappa_d \sum_{\ell=0}^{k-2} \binom{n-2}{\ell} \int_0^{r_{n,k}(x)} \bigl(c_0 t r_{n,k}(x)^{d-1}\bigr)^\ell \bigl(1-c_0 t r_{n,k}(x)^{d-1}\bigr)^{n-2-\ell} t^{d-1} \mathrm{d}t\\&\quad =f_+ d \kappa_d \sum_{\ell=0}^{k-2} \binom{n-2}{\ell} \int_0^{r_{n,k}(x)} \bigl(c_0 t r_{n,k}(x)^{d-1}\bigr)^\ell\\& \quad\quad \times\exp \bigl( (n-2-\ell) \log\!(1-c_0 t r_{n,k}(x)^{d-1})\bigr) t^{d-1} \mathrm{d}t\\&\quad \le f_+d \kappa_d \sum_{\ell=0}^{k-2} \binom{n-2}{\ell} \int_0^{r_{n,k}(x)} \bigl(c_0 t r_{n,k}(x)^{d-1}\bigr)^\ell\\& \quad\quad \times \exp \bigl( -c_0(n-2-\ell) t r_{n,k}(x)^{d-1}\bigr) t^{d-1} \mathrm{d}t.\end{align*}
Here the last line follows from the inequality
![]() $\log s \le s-1,\,s>0$
. Next we apply the change of variables
$\log s \le s-1,\,s>0$
. Next we apply the change of variables
which shows that the last upper bound takes the form
 \begin{equation}f_+d \kappa_d {c_0^{-d}} r_{n,k}(x)^{d(1-d)} \sum_{\ell=0}^{k-2} \binom{n-2}{\ell} (n-2-\ell)^{-d-\ell} \int_0^{c_0 (n-2-\ell)r_{n,k}(x)^d} s^{\ell+d-1} \,{\mathrm{e}}^{-s} \,\mathrm{d}s.\end{equation}
\begin{equation}f_+d \kappa_d {c_0^{-d}} r_{n,k}(x)^{d(1-d)} \sum_{\ell=0}^{k-2} \binom{n-2}{\ell} (n-2-\ell)^{-d-\ell} \int_0^{c_0 (n-2-\ell)r_{n,k}(x)^d} s^{\ell+d-1} \,{\mathrm{e}}^{-s} \,\mathrm{d}s.\end{equation}
We now use the bounds
![]() $f_- \kappa_d r_{n,k}(x)^d \le v_{n,k}$
,
$f_- \kappa_d r_{n,k}(x)^d \le v_{n,k}$
,
![]() $\binom{n-2}{\ell}\le n^{\ell}/\ell!$
, and the fact that the integral figuring in (13) converges as
$\binom{n-2}{\ell}\le n^{\ell}/\ell!$
, and the fact that the integral figuring in (13) converges as
![]() $n \to \infty$
. Hence the expression in (13) is bounded from above by
$n \to \infty$
. Hence the expression in (13) is bounded from above by
![]() $c_1 n^{-1} (\!\log n)^{1-d}$
, where
$c_1 n^{-1} (\!\log n)^{1-d}$
, where
![]() $c_1$
is some positive constant. Consequently (8) is bounded from above by
$c_1$
is some positive constant. Consequently (8) is bounded from above by
 \begin{align}&c_1 n^{-1}(\!\log n)^{1-d} \lambda(S(\textbf{j},2k)) \sup_{y \in S(\textbf{j},2k)} \mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(y,r_{n,k}(y)))\le k-1\bigr) \notag\\ &\quad \sim c_2 n^{-3} (\!\log n)^{2-d+\varepsilon} \end{align}
\begin{align}&c_1 n^{-1}(\!\log n)^{1-d} \lambda(S(\textbf{j},2k)) \sup_{y \in S(\textbf{j},2k)} \mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(y,r_{n,k}(y)))\le k-1\bigr) \notag\\ &\quad \sim c_2 n^{-3} (\!\log n)^{2-d+\varepsilon} \end{align}
for some
![]() $c_2>0$
.
$c_2>0$
.
By analogy with the reasoning above, (9) is given by the integral
 \begin{align}&2\int_{S(\textbf{j},2k)}\int_{S(\textbf{j},2k) \setminus B(x,r_{n,k}(x))}\mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\} \cup \{x\})(B(y,r_{n,k}(y))) \le k-1\bigr)\notag\\&\quad \times \mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(y)))\le k-1\bigr) \notag\\& \quad \times1\!\!1{\{r_{n,k}(y) \le r_{n,k}(x)\}} \mu(\mathrm{d}y)\,\mu(\mathrm{d}x). \end{align}
\begin{align}&2\int_{S(\textbf{j},2k)}\int_{S(\textbf{j},2k) \setminus B(x,r_{n,k}(x))}\mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\} \cup \{x\})(B(y,r_{n,k}(y))) \le k-1\bigr)\notag\\&\quad \times \mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(y)))\le k-1\bigr) \notag\\& \quad \times1\!\!1{\{r_{n,k}(y) \le r_{n,k}(x)\}} \mu(\mathrm{d}y)\,\mu(\mathrm{d}x). \end{align}
If
![]() $y \notin B(x,r_{n,k}(x))$
and
$y \notin B(x,r_{n,k}(x))$
and
![]() $r_{n,k}(x)\ge r_{n,k}(y)$
, we have the lower bound
$r_{n,k}(x)\ge r_{n,k}(y)$
, we have the lower bound
Since
![]() $f_+ \kappa_d r_{n,k}(x)^d \geq v_{n,k}$
, we find a constant
$f_+ \kappa_d r_{n,k}(x)^d \geq v_{n,k}$
, we find a constant
![]() $c_3>0$
such that
$c_3>0$
such that
whence
 \begin{align*}&\mathbb{P} \bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(y)))\le k-1\bigr)\\&\quad \le \sum_{\ell=0}^{k-1} \binom{n-2}{\ell} (c_3v_{n,k})^\ell (1-c_3v_{n,k})^{n-2-\ell}\\&\quad \sim \dfrac{c_3^{k-1}}{(k-1)!} (\!\log n)^{k-1} \exp (n \log (1-c_3v_{n,k}))\end{align*}
\begin{align*}&\mathbb{P} \bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(x,r_{n,k}(x))\setminus B(y,r_{n,k}(y)))\le k-1\bigr)\\&\quad \le \sum_{\ell=0}^{k-1} \binom{n-2}{\ell} (c_3v_{n,k})^\ell (1-c_3v_{n,k})^{n-2-\ell}\\&\quad \sim \dfrac{c_3^{k-1}}{(k-1)!} (\!\log n)^{k-1} \exp (n \log (1-c_3v_{n,k}))\end{align*}
as
![]() $n \to \infty$
. Since
$n \to \infty$
. Since
![]() $\log s \le s-1$
for
$\log s \le s-1$
for
![]() $s>0$
, (15) is bounded from above by
$s>0$
, (15) is bounded from above by
 \begin{align}&c_4 n^{-c_3} \lambda(S(\textbf{j},2k))^2 \sup_{y \in S(\textbf{j},2k)} \mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(y,r_{n,k}(y)))\le k-1\bigr)\notag\\&\quad \sim c_5 (4k+1)^{2d} \dfrac{(\!\log n)^{2+2\varepsilon}}{n^{3+c_3}}, \end{align}
\begin{align}&c_4 n^{-c_3} \lambda(S(\textbf{j},2k))^2 \sup_{y \in S(\textbf{j},2k)} \mathbb{P}\bigl(\#(\mathcal{X}_n \setminus \{X_i,X_{i^{\prime}}\})(B(y,r_{n,k}(y)))\le k-1\bigr)\notag\\&\quad \sim c_5 (4k+1)^{2d} \dfrac{(\!\log n)^{2+2\varepsilon}}{n^{3+c_3}}, \end{align}
where
![]() $c_4$
and
$c_4$
and
![]() $c_5$
are positive constants. Summing over all
$c_5$
are positive constants. Summing over all
![]() $i\neq i^{\prime}\leq n$
, it follows from (14) and (16) that
$i\neq i^{\prime}\leq n$
, it follows from (14) and (16) that
![]() $R(n)={\mathrm{O}}(n^{-1}(\!\log n)^{2-d+\varepsilon})$
as
$R(n)={\mathrm{O}}(n^{-1}(\!\log n)^{2-d+\varepsilon})$
as
![]() $n \to \infty$
, which finishes the proof of Lemma 2.
$n \to \infty$
, which finishes the proof of Lemma 2.
2.2.3. A Poisson approximation result based on the Chen–Stein method
In this subsection we recall a Poisson approximation result due to Arratia et al. [Reference Arratia, Goldstein and Gordon2], which is based on the Chen–Stein method. To this end, we consider a finite or countable collection
![]() $(Y_\alpha)_{\alpha\in I}$
of
$(Y_\alpha)_{\alpha\in I}$
of
![]() $\{0, 1\}$
-valued random variables and we let
$\{0, 1\}$
-valued random variables and we let
![]() $p_\alpha = \mathbb{P}(Y_\alpha=1)>0$
,
$p_\alpha = \mathbb{P}(Y_\alpha=1)>0$
,
![]() $p_{\alpha\beta}=\mathbb{P}(Y_\alpha=1, Y_\beta=1)$
. Moreover, suppose that for each
$p_{\alpha\beta}=\mathbb{P}(Y_\alpha=1, Y_\beta=1)$
. Moreover, suppose that for each
![]() $\alpha\in I$
there is a set
$\alpha\in I$
there is a set
![]() $B_\alpha\subset I$
that contains
$B_\alpha\subset I$
that contains
![]() $\alpha$
. The set
$\alpha$
. The set
![]() $B_\alpha$
is regarded as a neighborhood of
$B_\alpha$
is regarded as a neighborhood of
![]() $\alpha$
that consists of the set of indices
$\alpha$
that consists of the set of indices
![]() $\beta$
such that
$\beta$
such that
![]() $Y_\alpha$
and
$Y_\alpha$
and
![]() $Y_\beta$
are not independent. Finally, put
$Y_\beta$
are not independent. Finally, put
Theorem 3. (Theorem 1 of [Reference Arratia, Goldstein and Gordon2].) Let
![]() $W=\sum_{\alpha \in I}Y_\alpha$
, and assume
$W=\sum_{\alpha \in I}Y_\alpha$
, and assume
![]() $\lambda\,:\!=\, \mathbb{E}(W) \in (0,\infty)$
. Then
$\lambda\,:\!=\, \mathbb{E}(W) \in (0,\infty)$
. Then
2.2.4. Proof of Theorem 2
Recall
![]() $v_{n,k}$
from (3) and
$v_{n,k}$
from (3) and
![]() $C_{n,k}$
from (4). Put
$C_{n,k}$
from (4). Put
The following lemma claims that the number
![]() $C_{n,k}$
of exceedances is close to the number of subcubes for which there exists at least one exceedance, i.e.
$C_{n,k}$
of exceedances is close to the number of subcubes for which there exists at least one exceedance, i.e.
![]() $\widehat{C}_{n,k}$
, and that
$\widehat{C}_{n,k}$
, and that
![]() $\widehat{C}_{n,k}$
can be approximated by a Poisson random variable.
$\widehat{C}_{n,k}$
can be approximated by a Poisson random variable.
Lemma 4. We have
-
(a)
 $\mathbb{P} (C_{n,k} \neq \widehat{C}_{n,k} ) = {\mathrm{O}} \bigl((\!\log n)^{1-d} \bigr)$
,
$\mathbb{P} (C_{n,k} \neq \widehat{C}_{n,k} ) = {\mathrm{O}} \bigl((\!\log n)^{1-d} \bigr)$
, -
(b)
 $d_{\mathrm{TV}}(\widehat{C}_{n,k}, \mathrm{Po}(\mathbb{E}[\widehat{C}_{n,k}]))\ = {\mathrm{O}} \bigl((\!\log n)^{1-d} \bigr)$
,
$d_{\mathrm{TV}}(\widehat{C}_{n,k}, \mathrm{Po}(\mathbb{E}[\widehat{C}_{n,k}]))\ = {\mathrm{O}} \bigl((\!\log n)^{1-d} \bigr)$
, -
(c)
 $\mathbb{E} [ \widehat{C}_{n,k}] = {\mathrm{e}}^{-t} + {\mathrm{O}} ( {\log\log n}/{\log n} )$
.
$\mathbb{E} [ \widehat{C}_{n,k}] = {\mathrm{e}}^{-t} + {\mathrm{O}} ( {\log\log n}/{\log n} )$
.
Proof. Assertion (a) is a direct consequence of Lemma 2 and of the inequalities
 \begin{align*}& \mathbb{P}(C_{n,k}\neq \widehat{C}_{n,k})\\& \quad = \mathbb{P} \bigl(\exists \textbf{j}\in\mathcal{V}_n, \exists i,\ell \text{ s.t. } X_i,X_\ell \in \textbf{j};\, \mu(B(X_i,R_{i,n,k})) \wedge \mu(B(X_{\ell},R_{\ell,n,k}))>v_{n,k} \bigr)\\& \quad \leq \sum_{\textbf{j}\in \mathcal{V}_n}\sum_{i\neq \ell \leq n}\operatorname{\mathbb{P}}\bigl({X_i,X_{\ell}\in \textbf{j};\, \mu(B(X_i,R_{i,n,k})) \wedge \mu(B(X_{\ell},R_{\ell,n,k}))>v_{n,k} }\bigr)\\& \quad \leq \dfrac{n}{(\!\log n)^{1+\varepsilon}}\times R(n).\end{align*}
\begin{align*}& \mathbb{P}(C_{n,k}\neq \widehat{C}_{n,k})\\& \quad = \mathbb{P} \bigl(\exists \textbf{j}\in\mathcal{V}_n, \exists i,\ell \text{ s.t. } X_i,X_\ell \in \textbf{j};\, \mu(B(X_i,R_{i,n,k})) \wedge \mu(B(X_{\ell},R_{\ell,n,k}))>v_{n,k} \bigr)\\& \quad \leq \sum_{\textbf{j}\in \mathcal{V}_n}\sum_{i\neq \ell \leq n}\operatorname{\mathbb{P}}\bigl({X_i,X_{\ell}\in \textbf{j};\, \mu(B(X_i,R_{i,n,k})) \wedge \mu(B(X_{\ell},R_{\ell,n,k}))>v_{n,k} }\bigr)\\& \quad \leq \dfrac{n}{(\!\log n)^{1+\varepsilon}}\times R(n).\end{align*}
To prove (b), we apply Theorem 3 to the collection
![]() $(Y_\alpha)_{\alpha\in I} = (M_{\textbf{j}})_{\textbf{j}\in \mathcal{V}_n}$
. Recall that, conditionally on the event
$(Y_\alpha)_{\alpha\in I} = (M_{\textbf{j}})_{\textbf{j}\in \mathcal{V}_n}$
. Recall that, conditionally on the event
![]() $\mathcal{E}_n$
, the random variables
$\mathcal{E}_n$
, the random variables
![]() $M_{\textbf{j}}$
and
$M_{\textbf{j}}$
and
![]() $M_{\textbf{j}^{\prime}}$
are independent provided that
$M_{\textbf{j}^{\prime}}$
are independent provided that
![]() $\texttt{d}(\textbf{j},\textbf{j}^{\prime})\geq 2k+1$
. With a slight abuse of notation, we omit conditioning on
$\texttt{d}(\textbf{j},\textbf{j}^{\prime})\geq 2k+1$
. With a slight abuse of notation, we omit conditioning on
![]() $\mathcal{E}_n$
since this event occurs with probability tending to 1 as
$\mathcal{E}_n$
since this event occurs with probability tending to 1 as
![]() $n \to \infty$
(Lemma 1) at a rate that is at least polynomial. The first two terms in (17) are
$n \to \infty$
(Lemma 1) at a rate that is at least polynomial. The first two terms in (17) are
where
The term
![]() $b_3$
figuring in (17) equals 0 since, conditionally on
$b_3$
figuring in (17) equals 0 since, conditionally on
![]() $\mathcal{E}_n$
, the random variable
$\mathcal{E}_n$
, the random variable
![]() $M_\textbf{j}$
is independent of the
$M_\textbf{j}$
is independent of the
![]() $\sigma$
-field
$\sigma$
-field
![]() $\sigma(M_{\textbf{j}^{\prime}}\,:\, \textbf{j}^{\prime}\not\in S(\textbf{j},2k))$
. Thus, according to Theorem 3, we have
$\sigma(M_{\textbf{j}^{\prime}}\,:\, \textbf{j}^{\prime}\not\in S(\textbf{j},2k))$
. Thus, according to Theorem 3, we have
First we deal with
![]() $b_1$
. As for the first assertion, note that for each
$b_1$
. As for the first assertion, note that for each
![]() $\textbf{j}\in \mathcal{V}_n$
, using symmetry, we obtain
$\textbf{j}\in \mathcal{V}_n$
, using symmetry, we obtain
 \begin{align*}p_\textbf{j} & = \mathbb{P} \biggl(\bigcup_{i\leq n}\{X_i\in \textbf{j}, \mu(B(X_i,R_{i,n,k})) >v_{n,k} \}\biggr) \\& \leq n \cdot \mathbb{P} \bigl( X_1\in \textbf{j}, \mu(B(X_1,R_{1,n,k})) >v_{n,k} \bigr)\\& = n \cdot \int_{\textbf{j}} \mathbb{P}(\mu(B(x,R_{1,n,k})) >v_{n,k}\mid X_1=x) f(x) {\mathrm{d}} x\\& \le n f^+ \lambda(\textbf{j}) \int_{\textbf{j}} \mathbb{P}(\mu(B(x,R_{1,n,k})) >v_{n,k}\mid X_1=x) \, \dfrac{1}{\lambda(\textbf{j})} {\mathrm{d}} x\\& = n f^+ \lambda(\textbf{j}) \mathbb{P}\bigl(\mu(B(\widetilde{X}_1,R_{1,n,k})) >v_{n,k}\bigr),\end{align*}
\begin{align*}p_\textbf{j} & = \mathbb{P} \biggl(\bigcup_{i\leq n}\{X_i\in \textbf{j}, \mu(B(X_i,R_{i,n,k})) >v_{n,k} \}\biggr) \\& \leq n \cdot \mathbb{P} \bigl( X_1\in \textbf{j}, \mu(B(X_1,R_{1,n,k})) >v_{n,k} \bigr)\\& = n \cdot \int_{\textbf{j}} \mathbb{P}(\mu(B(x,R_{1,n,k})) >v_{n,k}\mid X_1=x) f(x) {\mathrm{d}} x\\& \le n f^+ \lambda(\textbf{j}) \int_{\textbf{j}} \mathbb{P}(\mu(B(x,R_{1,n,k})) >v_{n,k}\mid X_1=x) \, \dfrac{1}{\lambda(\textbf{j})} {\mathrm{d}} x\\& = n f^+ \lambda(\textbf{j}) \mathbb{P}\bigl(\mu(B(\widetilde{X}_1,R_{1,n,k})) >v_{n,k}\bigr),\end{align*}
where
![]() $\widetilde{X}_1$
is independent of
$\widetilde{X}_1$
is independent of
![]() $X_2,\ldots,X_n$
and has a uniform distribution over
$X_2,\ldots,X_n$
and has a uniform distribution over
![]() $\textbf{j}$
. Invoking Remark 4, the probability figuring in the last line is asymptotically equal to
$\textbf{j}$
. Invoking Remark 4, the probability figuring in the last line is asymptotically equal to
![]() ${\mathrm{e}}^{-t}/n$
as
${\mathrm{e}}^{-t}/n$
as
![]() $n \to \infty$
. Since
$n \to \infty$
. Since
![]() $\lambda(\textbf{j})={\mathrm{O}}( (\!\log n)^{1+\varepsilon}/n)$
, we thus have
$\lambda(\textbf{j})={\mathrm{O}}( (\!\log n)^{1+\varepsilon}/n)$
, we thus have
where C is a constant that does not depend on
![]() $\textbf{j}$
. Since
$\textbf{j}$
. Since
![]() $\#\mathcal{V}_n\leq {n}/{ (\!\log n)^{1+\varepsilon}}$
and
$\#\mathcal{V}_n\leq {n}/{ (\!\log n)^{1+\varepsilon}}$
and
![]() $\#S(\textbf{j}, 2k)\leq (4k+1)^d$
, summing over
$\#S(\textbf{j}, 2k)\leq (4k+1)^d$
, summing over
![]() $\textbf{j},\textbf{j}^{\prime}$
gives
$\textbf{j},\textbf{j}^{\prime}$
gives
 \begin{equation*}b_1 \leq C^2 \sum_{\textbf{j}\in \mathcal{V}_n}\sum_{\textbf{j}^{\prime}\in S(\textbf{j},2k)} \biggl( \dfrac{(\!\log n)^{1+\varepsilon}}{n} \biggr)^2 = {\mathrm{O}}\biggl( \dfrac{(\!\log n)^{1+\varepsilon}}{n} \biggr).\end{equation*}
\begin{equation*}b_1 \leq C^2 \sum_{\textbf{j}\in \mathcal{V}_n}\sum_{\textbf{j}^{\prime}\in S(\textbf{j},2k)} \biggl( \dfrac{(\!\log n)^{1+\varepsilon}}{n} \biggr)^2 = {\mathrm{O}}\biggl( \dfrac{(\!\log n)^{1+\varepsilon}}{n} \biggr).\end{equation*}
To deal with
![]() $b_2$
, note that for each
$b_2$
, note that for each
![]() $\textbf{j},\textbf{j}^{\prime}\in \mathcal{V}_n$
and
$\textbf{j},\textbf{j}^{\prime}\in \mathcal{V}_n$
and
![]() $\textbf{j}^{\prime}\in S(\textbf{j},2k)$
we have
$\textbf{j}^{\prime}\in S(\textbf{j},2k)$
we have
 \begin{align*}p_{\textbf{j}\textbf{j}^{\prime}} & = \mathbb{P} \biggl( \bigcup_{i\neq i^{\prime}\leq n} \{ X_i\in \textbf{j}, X_{i^{\prime}}\in S(\textbf{j},2k), \mu(B(X_i,R_{i,n,k}))\wedge \mu(B(X_{i^{\prime}},R_{i^{\prime},n,k})) >v_{n,k} \} \biggr)\\& \leq \mathbb{P} \biggl( \bigcup_{i\neq i^{\prime}\leq n} \{ X_i, X_{i^{\prime}}\in S(\textbf{j},2k);\, \mu(B(X_i,R_{i,n,k})) \wedge \mu(B(X_{i^{\prime}},R_{i^{\prime},n,k})) >v_{n,k} \} \biggr).\end{align*}
\begin{align*}p_{\textbf{j}\textbf{j}^{\prime}} & = \mathbb{P} \biggl( \bigcup_{i\neq i^{\prime}\leq n} \{ X_i\in \textbf{j}, X_{i^{\prime}}\in S(\textbf{j},2k), \mu(B(X_i,R_{i,n,k}))\wedge \mu(B(X_{i^{\prime}},R_{i^{\prime},n,k})) >v_{n,k} \} \biggr)\\& \leq \mathbb{P} \biggl( \bigcup_{i\neq i^{\prime}\leq n} \{ X_i, X_{i^{\prime}}\in S(\textbf{j},2k);\, \mu(B(X_i,R_{i,n,k})) \wedge \mu(B(X_{i^{\prime}},R_{i^{\prime},n,k})) >v_{n,k} \} \biggr).\end{align*}
Using subadditivity, and taking the supremum, we obtain
 \begin{align*}& b_2 \leq\\&\ \sum_{\textbf{j}\in \mathcal{V}_n}\sum_{\textbf{j}^{\prime}\in S(\textbf{j},2k)} \sup_{\textbf{j}\in\mathcal{V}_n}\sum_{i\neq i^{\prime}\leq n}\mathbb{P} \bigl(X_i,X_{i^{\prime}}\in S(\textbf{j},2k);\, \mu(B(X_i,R_{i,n,k})) \wedge\mu(B(X_{i^{\prime}},R_{i^{\prime},n,k}))>v_{n,k}\bigr) . \end{align*}
\begin{align*}& b_2 \leq\\&\ \sum_{\textbf{j}\in \mathcal{V}_n}\sum_{\textbf{j}^{\prime}\in S(\textbf{j},2k)} \sup_{\textbf{j}\in\mathcal{V}_n}\sum_{i\neq i^{\prime}\leq n}\mathbb{P} \bigl(X_i,X_{i^{\prime}}\in S(\textbf{j},2k);\, \mu(B(X_i,R_{i,n,k})) \wedge\mu(B(X_{i^{\prime}},R_{i^{\prime},n,k}))>v_{n,k}\bigr) . \end{align*}
Therefore
According to Lemma 2, the last term equals
![]() ${\mathrm{O}}\bigl((\!\log n)^{1-d} \bigr)$
, which concludes the proof of (b).
${\mathrm{O}}\bigl((\!\log n)^{1-d} \bigr)$
, which concludes the proof of (b).
To prove (c), observe that
By Theorem 1, the last summand is
![]() ${\mathrm{O}} ( {\log\log n}/{\log n} )$
. Since
${\mathrm{O}} ( {\log\log n}/{\log n} )$
. Since
![]() $C_{n,k} \ge \widehat{C}_{n,k}$
, we further have
$C_{n,k} \ge \widehat{C}_{n,k}$
, we further have
 \begin{align*}|\mathbb{E} [\widehat{C}_{n,k}] - \mathbb{E}[C_{n,k}]| & = \mathbb{E} [C_{n,k}-\widehat{C}_{n,k}]\\& = \mathbb{E} \biggl( \sum_{i\leq n} 1\!\!1 \{\mu(B(X_i, R_{i,n,k}))>v_{n,k}\} - \sum_{\textbf{j}\in\mathcal{V}_n} 1\!\!1 \{M_\textbf{j}>v_{n,k}\} \biggr)\\& = \sum_{\textbf{j}\in\mathcal{V}_n} \mathbb{E} \Biggl[ \biggl( \sum_{i\leq n} 1\!\!1\{X_i\in \textbf{j}\} 1\!\!1 \{\mu(B(X_i,R_{i,n,k})) > v_{n,k} \} - 1 \biggr)1\!\!1 \{M_\textbf{j}>v_{n,k}\} \Biggr]\\& \leq \sum_{\textbf{j}\in \mathcal{V}_n}\sum_{i\neq i^{\prime}\leq n} \mathbb{P} (X_i,X_{i^{\prime}}\in \textbf{j}, \mu(B(X_i,R_{i,n,k})), \mu(B(X_{i^{\prime}},R_{i^{\prime},n,k}))> v_{n,k} )\\& \leq \#\mathcal{V}_n \times R(n).\end{align*}
\begin{align*}|\mathbb{E} [\widehat{C}_{n,k}] - \mathbb{E}[C_{n,k}]| & = \mathbb{E} [C_{n,k}-\widehat{C}_{n,k}]\\& = \mathbb{E} \biggl( \sum_{i\leq n} 1\!\!1 \{\mu(B(X_i, R_{i,n,k}))>v_{n,k}\} - \sum_{\textbf{j}\in\mathcal{V}_n} 1\!\!1 \{M_\textbf{j}>v_{n,k}\} \biggr)\\& = \sum_{\textbf{j}\in\mathcal{V}_n} \mathbb{E} \Biggl[ \biggl( \sum_{i\leq n} 1\!\!1\{X_i\in \textbf{j}\} 1\!\!1 \{\mu(B(X_i,R_{i,n,k})) > v_{n,k} \} - 1 \biggr)1\!\!1 \{M_\textbf{j}>v_{n,k}\} \Biggr]\\& \leq \sum_{\textbf{j}\in \mathcal{V}_n}\sum_{i\neq i^{\prime}\leq n} \mathbb{P} (X_i,X_{i^{\prime}}\in \textbf{j}, \mu(B(X_i,R_{i,n,k})), \mu(B(X_{i^{\prime}},R_{i^{\prime},n,k}))> v_{n,k} )\\& \leq \#\mathcal{V}_n \times R(n).\end{align*}
According to Lemma 2, the last term equals
![]() ${\mathrm{O}}\bigl((\!\log n)^{1-d} \bigr)$
. This concludes the proof of Lemma 4 and thus of Theorem 2.
${\mathrm{O}}\bigl((\!\log n)^{1-d} \bigr)$
. This concludes the proof of Lemma 4 and thus of Theorem 2.
3. Concluding remarks
When dealing with limit laws for large kth-nearest neighbor distances of a sequence of i.i.d. random points in
![]() $\mathbb{R}^d$
with density f, which take values in a bounded region K, the modification of the kth-nearest neighbor distances made in (6) (by introducing the ‘boundary distances’
$\mathbb{R}^d$
with density f, which take values in a bounded region K, the modification of the kth-nearest neighbor distances made in (6) (by introducing the ‘boundary distances’
![]() $\|X_i - \partial K\|$
) and the condition that f is bounded away from zero, which have been adopted in [Reference Henze12] and [Reference Henze13], seem to be crucial, since boundary effects play a decisive role [Reference Dette and Henze8, Reference Dette and Henze9]. Regarding kth-nearest neighbor balls with large probability volume, there is no need to introduce
$\|X_i - \partial K\|$
) and the condition that f is bounded away from zero, which have been adopted in [Reference Henze12] and [Reference Henze13], seem to be crucial, since boundary effects play a decisive role [Reference Dette and Henze8, Reference Dette and Henze9]. Regarding kth-nearest neighbor balls with large probability volume, there is no need to introduce
![]() $\|X_i - \partial K\|$
. It is an open problem, however, whether Theorem 2 continues to hold for densities that are not bounded away from zero.
$\|X_i - \partial K\|$
. It is an open problem, however, whether Theorem 2 continues to hold for densities that are not bounded away from zero.
A second open problem refers to Theorem 1, which states convergence of expectations of
![]() $C_{n,k}$
in a setting beyond the finite-dimensional case. Since
$C_{n,k}$
in a setting beyond the finite-dimensional case. Since
![]() $C_{n,k}$
is non-negative, the sequence
$C_{n,k}$
is non-negative, the sequence
![]() $(C_{n,k})_{k}$
is tight by Markov’s inequality. Can one find conditions on the underlying distribution that ensure convergence in distribution to some random element of the metric space?
$(C_{n,k})_{k}$
is tight by Markov’s inequality. Can one find conditions on the underlying distribution that ensure convergence in distribution to some random element of the metric space?
Acknowledgements
The authors would like to thank an anonymous referee and an Associate Editor for many valuable remarks.
Funding information
There are no funding bodies to thank relating to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.