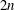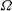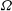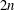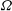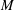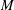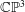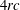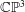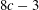A trisymplectic structure on a complex 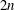2n$2n$-manifold is a three-dimensional space 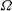{\rm\Omega}${\rm\Omega}$ of closed holomorphic forms such that any element of 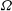{\rm\Omega}${\rm\Omega}$ has constant rank 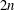2n$2n$, n$n$ or zero, and degenerate forms in 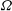{\rm\Omega}${\rm\Omega}$ belong to a non-degenerate quadric hypersurface. We show that a trisymplectic manifold is equipped with a holomorphic 3-web and the Chern connection of this 3-web is holomorphic, torsion-free, and preserves the three symplectic forms. We construct a trisymplectic structure on the moduli of regular rational curves in the twistor space of a hyperkähler manifold, and define a trisymplectic reduction of a trisymplectic manifold, which is a complexified form of a hyperkähler reduction. We prove that the trisymplectic reduction in the space of regular rational curves on the twistor space of a hyperkähler manifold 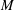M$M$ is compatible with the hyperkähler reduction on 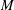M$M$. As an application of these geometric ideas, we consider the ADHM construction of instantons and show that the moduli space of rank r$r$, charge c$c$ framed instanton bundles on 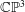\mathbb{C}\mathbb{P}^{3}$\mathbb{C}\mathbb{P}^{3}$ is a smooth trisymplectic manifold of complex dimension 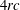4rc$4rc$. In particular, it follows that the moduli space of rank two, charge c$c$ instanton bundles on 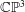\mathbb{C}\mathbb{P}^{3}$\mathbb{C}\mathbb{P}^{3}$ is a smooth complex manifold dimension 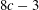8c-3$8c-3$, thus settling part of a 30-year-old conjecture.

For any integer $m\geq 4$ we construct twistor spaces of algebraic dimension a = 2 associated to some self-dual structures on mP2, the connected sum of m complex projective planes P2. Together with previously known results this implies that for any $m\geq 5$ all the possible values for algebraic dimension $0\leq a \leq 3$ are attained for some such twistor spaces. Our method is to construct such twistor spaces by small deformations of Joyce twistor spaces.

We show that for any positive integer τ there exist on $4{\Bbb CP}$2, the connected sum of four complex projective planes, twistor spaces whose algebraic dimensions are two. Here, τ appears as the order of the normal bundle of C in S, where S is a real smooth half-anti-canonical divisor on the twistor space and C is a real smooth anti-canonical divisor on S. This completely answers the problem posed by Campana and Kreussler. Our proof is based on the method developed by Honda, which can be regarded as a generalization of the theory of Donaldson and Friedman.