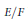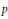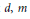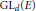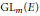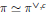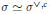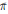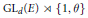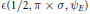1 results
Expression d'un facteur epsilon de paire par une formule intégrale
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 5 / 01 October 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 993-1049
- Print publication:
- 01 October 2014
-
- Article
-
- You have access
- Export citation
-
Let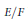
$E/F$ be a quadratic extension of 
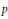$p$-adic fields and let 
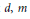$d,\,m$ be nonnegative integers of distinct parities. Fix admissible irreducible tempered representations 
$\pi $ and 
$\sigma $ of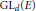 
$\text{G}{{\text{L}}_{d}}\left( E \right)$ and 
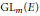$\text{G}{{\text{L}}_{m}}\left( E \right)$ respectively. We assume that $\pi $ and $\sigma $ are conjugate-dual. That is to say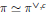 
$\pi \,\simeq \,{{\pi }^{\vee \text{,}\,c}}$ and 
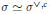$\sigma \,\simeq \,{{\sigma }^{\vee ,c}}$ where 
$c$ is the nontrivial 
$F$-automorphism of 
$E$. This implies that we can extend $\pi $ to an unitary representation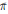 
$\tilde{\pi }$ of a nonconnected group 
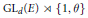$\text{G}{{\text{L}}_{d}}\left( E \right)\,\rtimes \,\left\{ 1,\,0 \right\}$. Define 
$\tilde{\sigma }$ the same way. We state and prove an integral formula for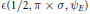 
$\in \left( 1/2,\,\pi \,\times \,\sigma ,\,{{\psi }_{E}} \right)$ involving the characters of 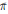$\tilde{\pi }$ and $\tilde{\sigma }$. This formula is related to the local Gan–Gross–Prasad conjecture for unitary groups.
