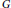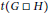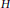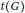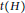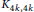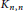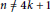1 results
The Thickness of the Cartesian Product of Two Graphs
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 705-720
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
-
The thickness of a graph 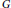G is the minimum number of planar subgraphs whose union is 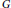G. A t-minimal graph is a graph of thickness t that contains no proper subgraph of thickness t. In this paper, upper and lower bounds are obtained for the thickness, 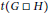t\left( G\,\square \,H \right), of the Cartesian product of two graphs 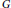G and 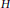H, in terms of the thickness 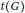t\left( G \right) and 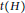t\left( H \right). Furthermore, the thickness of the Cartesian product of two planar graphs and of a t-minimal graph and a planar graph are determined. By using a new planar decomposition of the complete bipartite graph 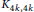{{K}_{4k,\,4k}}, the thickness of the Cartesian product of two complete bipartite graphs 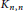{{K}_{n,n}} and 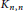{{K}_{n,n}} is also given for 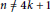n\,\ne \,4k\,+\,1.
