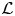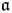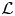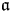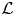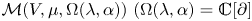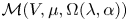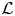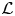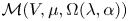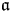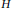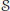The Virasoro algebra 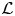 $\mathcal {L}$ is an infinite-dimensional Lie algebra with basis {Lm, C| m ∈ ℤ} and relations [Lm, Ln] = (n − m)Lm+n + δm+n,0((m3 − m)/12)C, [Lm, C] = 0 for m, n ∈ ℤ. Let
$\mathcal {L}$ is an infinite-dimensional Lie algebra with basis {Lm, C| m ∈ ℤ} and relations [Lm, Ln] = (n − m)Lm+n + δm+n,0((m3 − m)/12)C, [Lm, C] = 0 for m, n ∈ ℤ. Let 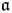 $\mathfrak a$ be the subalgebra of
$\mathfrak a$ be the subalgebra of 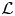 $\mathcal {L}$ spanned by Li for i ≥ −1. For any triple (μ, λ, α) of complex numbers with μ ≠ 0, λ ≠ 0 and any non-trivial
$\mathcal {L}$ spanned by Li for i ≥ −1. For any triple (μ, λ, α) of complex numbers with μ ≠ 0, λ ≠ 0 and any non-trivial 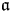 $\mathfrak a$-module V satisfying the condition: for any v ∈ V there exists a non-negative integer m such that Liv = 0 for all i ≥ m, non-weight
$\mathfrak a$-module V satisfying the condition: for any v ∈ V there exists a non-negative integer m such that Liv = 0 for all i ≥ m, non-weight 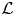 $\mathcal {L}$-modules on the linear tensor product of V and ℂ[∂], denoted by
$\mathcal {L}$-modules on the linear tensor product of V and ℂ[∂], denoted by 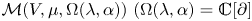 $\mathcal {M}(V,\mu ,\Omega (\lambda ,\alpha ))\ (\Omega (\lambda ,\alpha )=\mathbb {C}[\partial ]$ as vector spaces), are constructed in this paper. We prove that
$\mathcal {M}(V,\mu ,\Omega (\lambda ,\alpha ))\ (\Omega (\lambda ,\alpha )=\mathbb {C}[\partial ]$ as vector spaces), are constructed in this paper. We prove that 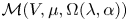 $\mathcal {M}(V,\mu ,\Omega (\lambda ,\alpha ))$ is simple if and only if μ ≠ 1, λ ≠ 0, α ≠ 0. We also give necessary and sufficient conditions for two such simple
$\mathcal {M}(V,\mu ,\Omega (\lambda ,\alpha ))$ is simple if and only if μ ≠ 1, λ ≠ 0, α ≠ 0. We also give necessary and sufficient conditions for two such simple 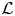 $\mathcal {L}$-modules being isomorphic. Finally, these simple
$\mathcal {L}$-modules being isomorphic. Finally, these simple 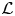 $\mathcal {L}$-modules
$\mathcal {L}$-modules 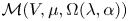 $\mathcal {M}(V,\mu ,\Omega (\lambda ,\alpha ))$ are proved to be new for V not being the highest weight
$\mathcal {M}(V,\mu ,\Omega (\lambda ,\alpha ))$ are proved to be new for V not being the highest weight 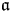 $\mathfrak a$-module whose highest weight is non-zero.
$\mathfrak a$-module whose highest weight is non-zero.