Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T07:33:34.322Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of Simple Weight Modules over the Schrödinger Algebra

Published online by Cambridge University Press:  20 November 2018

V. V. Bavula  and
T. Lu
V. V. Bavula
Affiliation:
Department of Pure Mathematics, University of Sheffield, Hicks Building, Sheffield Sh 6RH, UK, e-mail: [email protected]
T. Lu
Affiliation:
School of Mathematical Sciences, Huaqiao University, Quanzhou, Fujian 362021, China, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

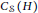A classification of simple weight modules over the Schrödinger algebra is given. The Krull and the global dimensions are found for the centralizer ${{C}_{S}}(H)$ (and some of its prime factor algebras) of the Cartan element 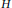$H$ in the universal enveloping algebra 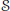$S$ of the Schrödinger (Lie) algebra. The simple 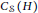${{C}_{S}}(H)$-modules are classified. The Krull and the global dimensions are found for some (prime) factor algebras of the algebra 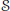$S$ (over the centre). It is proved that some (prime) factor algebras of 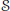$S$ and 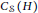${{C}_{S}}(H)$ are tensor homological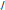$/$Krull minimal.

Keywords

17B1017B2017B3516E1016P9016P4016P50weight modulesimple modulecentralizerKrull dimensionglobal dimensiontensor homological minimal algebratensor Krull minimal algebra
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 1 , 01 March 2018 , pp. 16 - 39
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Auslander, M., On the dimension ofmodules and algebras. III. Global dimension. Nagoya Math. J. 9 (1955), 66–77. http://dx.doi.org/10.1017/S0027763000023291.Google Scholar
[2] Bavula, V. V., Finite-dimensionality of Extn and Torn of simple modules over a class of algebras. Funct. Anal. Appl. 25(1991) no. 3, 229–230. http://dx.doi.org/!0.1007/BF01085496.Google Scholar
[3] Bavula, V. V., Simple D[X, Y; a, a]-modules. Ukrainian Math. J. 44 (1992), no. 12, 1500–1511. http://dx.doi.Org/10.1007/BF01061 275.Google Scholar
[4] Bavula, V. V., Generalized Weyl algebras, kernet and tensor-simple algebras, their simple modules. In: Representations of algebras (Ottawa, 1992), CMS Conf. Proc, 14, American Mathematical Society, Providence, RI, 1993, pp. 83-107.Google Scholar
[5] Bavula, V. V., Description oftwo-sided Ideals in a class of noncommutative rings. I. Ukrainian Math. J. 45 (1993), no. 2, 223–234. http://dx.doi.org/10.1007/BF01060977.Google Scholar
[6] Bavula, V. V., Generalized Weyl algebras and their representations. St. Petersburg Math. J. 4 (1993), no. 1, 71–92.Google Scholar
[7] Bavula, V. V., Global dimension of generalized Weyl algebras. In: Representation of Algebras (Cocoyoc, 1994), CMS Conf. Proc, 18, American Mathematical Society, Providence, RI, 1996, pp. 81-107.Google Scholar
[8] Bavula, V. V., Tensor homological minimal algebras, global dimension ofthe tensor product of algebras and of generalized Weyl algebras. Bull. Sei. Math. 120 (1996), no. 3, 293–335.Google Scholar
[9] Bavula, V. V. and Lenagan, T., Krull dimension of generalized Weyl algebras with noncommutative coefficients. J. Algebra 235 (2001), 315–358. http://dx.doi.Org/10.1006/jabr.2000.8466.Google Scholar
[10] Bavula, V. V. and Lenagan, T., Generalized Weyl algebras are tensor Krull minimal. J. Algebra 239 (2001), 93–111. http://dx.doi.Org/10.1006/jabr.2000.8641.Google Scholar
[11] Bavula, V. V. and Lu, T., The prime spectrum and simple modules over the quantum spatial ageing algebra. Algebr. Represent. Theory 19 (2016), no. 5, 1109–1133. http://dx.doi.org/10.1007/s10468-016-9613-8.Google Scholar
[12] Bavula, V. V. and Lu, T., Prime ideals ofthe enveloping algebra ofthe Euclidean algebra and a classification ofits simple weight modules. J. Math. Phys. 58(2017), no. 1, 011701, 33. http://dx.doi.Org/10.1063/1.4973378.Google Scholar
[13] Bavula, V. V. and Lu, T., Torsion simple modules over the quantum spatial ageing algebra. Commun. Algebra (published online 26 Oct. 2016). http://dx.doi.org/10.1080/00927872.2016.1240177.Google Scholar
[14] Bavula, V. V. and Lu, T., The universal enveloping algebra U(sl 2 ⋉ V2), its prime spectrum and a classification of its simple weight modules. J. Lie Theory, to appear.Google Scholar
[15] Bavula, V. V. and Lu, T., The universal enveloping algebra ofthe Schrödinger algebra and its prime spectrum. Bull. Lond. Math. Soc, to appear.Google Scholar
[16] Bavula, V. V. and Van Oystaeyen, F., Krull dimension of generalized Weyl algebras and iterated skew polynomial rings: commutative coefficients. J. Algebra 208 (1998), 1–34. http://dx.doi.org/10.1006/jabr.1998.7482.Google Scholar
[17] Block, R. E., The irreducible representations ofthe Lie algebra s 1(2) and ofthe Weyl algebra. Adv. Math. 39 (1981), 69–110. http://dx.doi.Org/10.1016/0001-8708(81)90058-XGoogle Scholar
[18] Dubsky, B., Classification of simple weight modules with finite-dimensional weight Spaces over the Schrödinger algebra. Linear Algebra Appl. 443 (2014), 204–214. http://dx.doi.Org/10.1016/j.laa.2O13.11.016.Google Scholar
[19] Dubsky, B., Lü, R., Mazorchuk, V., and Zhao, K., Category O for the Schrödinger algebra. Linear Algebra Appl. 460 (2014), 17–50. http://dx.doi.Org/10.1016/j.laa.2O14.07.030.Google Scholar
[20] Dobrev, V., Doebner, H. D., and Mrugalla, C., Lowest weight representations ofthe Schrödinger algebra and generalized heat/Schrödinger equations. Reports on Mathematical Physics 39 (1997), 201–218. http://dx.doi.Org/10.1016/S0034-4877(97)88001-9.Google Scholar
[21] Hodges, T. J., Noncommutative deformation of type-A Kleinian singularities. J. Algebra 161(1993) no. 2, 271–290. http://dx.doi.org/10.1006/jabr.1993.1219.Google Scholar
[22] Lü, R., Mazorchuk, V., and Zhao, K., Classification of simple weight modules over the 1-spatial ageing algebra. Algebr. Represent. Theory 18 (2015), no. 2, 381–395. http://dx.doi.Org/10.1007/s10468-014-9499-2.Google Scholar
[23] McConnell, J. C. and Robson, J. C., Noncommutative noetherian rings. Graduate Studies in Mathematics, 30, American Mathematical Society, Providence, RI, 2001. http://dx.doi.Org/10.1090/gsm/030.Google Scholar
[24] Perroud, M., Projective representations of the Schrödinger group. Helv. Phys. Acta 50 (1977), 233–252.Google Scholar
[25] Reinhart, G. S., Note on the global dimension ofa certain ring. Proc. Amer. Math. Soc. 13 (1962), 341–346. http://dx.doi.org/10.1090/S0002-9939-1962-0137747-7.Google Scholar
[26] Rentschier, R. and Gabriel, P., Sur la dimension des anneaux et ensembles ordonnes. C. R. Acad. Sei. Paris Ser. A-B, 265(1967), A712-A715.Google Scholar
[27] Smith, S. P., Krull dimension ofthe enveloping algebra ofsl(2). J. Algebra 71 (1981), 89–94. http://dx.doi.Org/10.1016/0021-8693(81)90114-9.Google Scholar
[28] Stafford, J. T., Homological properties ofthe enveloping algebra U(sl 2). Math. Proc. Camb. Phil. Soc. 91 (1982), no. 1, 29–37. http://dx.doi.org/10.1017/S0305004100059089Google Scholar
[29] Wu, Y. and Zhu, L., Simple weight modules for Schrödinger algebra. Linear Algebra Appl. 438 (2013), 559–563. http://dx.doi.Org/10.1016/j.laa.2O12.07.029.Google Scholar
[30] Zhang, X. and Cheng, Y., Simple Schrödinger modules which are locally finite over the positive part. J. Pure Appl. Algebra 219 (2015), 2799–2815. http://dx.doi.Org/10.1016/j.jpaa.2O14.09.029Google Scholar