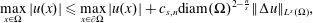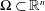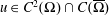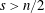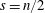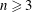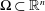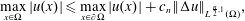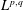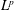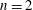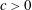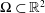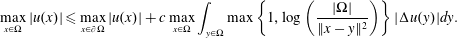1 results
An Endpoint Alexandrov Bakelman Pucci Estimate in the Plane
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 11 January 2019, pp. 643-651
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
-
The classical Alexandrov–Bakelman–Pucci estimate for the Laplacian states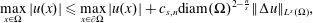
where
$$\begin{eqnarray}\max _{x\in \unicode[STIX]{x03A9}}|u(x)|\leqslant \max _{x\in \unicode[STIX]{x2202}\unicode[STIX]{x03A9}}|u(x)|+c_{s,n}\text{diam}(\unicode[STIX]{x03A9})^{2-\frac{n}{s}}\Vert \unicode[STIX]{x0394}u\Vert _{L^{s}(\unicode[STIX]{x03A9})},\end{eqnarray}$$
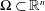$\unicode[STIX]{x03A9}\subset \mathbb{R}^{n}$, 
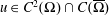$u\in C^{2}(\unicode[STIX]{x03A9})\cap C(\overline{\unicode[STIX]{x03A9}})$ and 
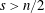$s>n/2$. The inequality fails for 
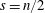$s=n/2$. A Sobolev embedding result of Milman and Pustylnik, originally phrased in a slightly different context, implies an endpoint inequality: if 
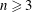$n\geqslant 3$ and 
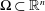$\unicode[STIX]{x03A9}\subset \mathbb{R}^{n}$ is bounded, then where
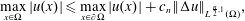$$\begin{eqnarray}\max _{x\in \unicode[STIX]{x03A9}}|u(x)|\leqslant \max _{x\in \unicode[STIX]{x2202}\unicode[STIX]{x03A9}}|u(x)|+c_{n}\Vert \unicode[STIX]{x0394}u\Vert _{L^{\frac{n}{2},1}(\unicode[STIX]{x03A9})},\end{eqnarray}$$
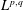$L^{p,q}$ is the Lorentz space refinement of 
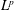$L^{p}$. This inequality fails for 
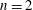$n=2$, and we prove a sharp substitute result: there exists 
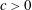$c>0$ such that for all 
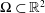$\unicode[STIX]{x03A9}\subset \mathbb{R}^{2}$ with finite measure, This is somewhat dual to the classical Trudinger–Moser inequality; we also note that it is sharper than the usual estimates given in Orlicz spaces; the proof is rearrangement-free. The Laplacian can be replaced by any uniformly elliptic operator in divergence form.
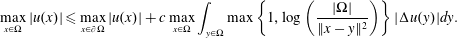$$\begin{eqnarray}\max _{x\in \unicode[STIX]{x03A9}}|u(x)|\leqslant \max _{x\in \unicode[STIX]{x2202}\unicode[STIX]{x03A9}}|u(x)|+c\max _{x\in \unicode[STIX]{x03A9}}\int _{y\in \unicode[STIX]{x03A9}}\max \left\{1,\log \left(\frac{|\unicode[STIX]{x03A9}|}{\Vert x-y\Vert ^{2}}\right)\right\}|\unicode[STIX]{x0394}u(y)|dy.\end{eqnarray}$$
