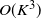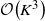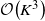Restless bandits are a class of sequential resource allocation problems concerned with allocating one or more resources among several alternative processes where the evolution of the processes depends on the resources allocated to them. Such models capture the fundamental trade-offs between exploration and exploitation. In 1988, Whittle developed an index heuristic for restless bandit problems which has emerged as a popular solution approach because of its simplicity and strong empirical performance. The Whittle index heuristic is applicable if the model satisfies a technical condition known as indexability. In this paper, we present two general sufficient conditions for indexability and identify simpler-to-verify refinements of these conditions. We then revisit a previously proposed algorithm called the adaptive greedy algorithm which is known to compute the Whittle index for a sub-class of restless bandits. We show that a generalization of the adaptive greedy algorithm computes the Whittle index for all indexable restless bandits. We present an efficient implementation of this algorithm which can compute the Whittle index of a restless bandit with K states in 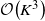 $\mathcal{O}\!\left(K^3\right)$ computations. Finally, we present a detailed numerical study which affirms the strong performance of the Whittle index heuristic.
$\mathcal{O}\!\left(K^3\right)$ computations. Finally, we present a detailed numerical study which affirms the strong performance of the Whittle index heuristic.
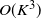 $O(K^3)$ algorithm to compute whittle index – CORRIGENDUM
$O(K^3)$ algorithm to compute whittle index – CORRIGENDUM
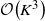 $\mathcal{O}\!\left(K^3\right)$ algorithm to compute Whittle index
$\mathcal{O}\!\left(K^3\right)$ algorithm to compute Whittle index