Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T11:27:41.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Conditions for indexability of restless bandits and an $\mathcal{O}\!\left(K^3\right)$ algorithm to compute Whittle index

Part of: Numerical methods in calculus of variations and optimal control Mathematical economics

Published online by Cambridge University Press:  14 June 2022

Nima Akbarzadeh Open the ORCID record for Nima Akbarzadeh [Opens in a new window]  and
Aditya Mahajan
Nima Akbarzadeh*
Affiliation:
McGill University
Aditya Mahajan*
Affiliation:
McGill University
*
*Postal address: Department of Electrical and Computer Engineering, McGill University, 3480 Rue University, Montréal, QC H3A 0E9.
*Postal address: Department of Electrical and Computer Engineering, McGill University, 3480 Rue University, Montréal, QC H3A 0E9.
Get access Rights & Permissions [Opens in a new window]

Abstract

Restless bandits are a class of sequential resource allocation problems concerned with allocating one or more resources among several alternative processes where the evolution of the processes depends on the resources allocated to them. Such models capture the fundamental trade-offs between exploration and exploitation. In 1988, Whittle developed an index heuristic for restless bandit problems which has emerged as a popular solution approach because of its simplicity and strong empirical performance. The Whittle index heuristic is applicable if the model satisfies a technical condition known as indexability. In this paper, we present two general sufficient conditions for indexability and identify simpler-to-verify refinements of these conditions. We then revisit a previously proposed algorithm called the adaptive greedy algorithm which is known to compute the Whittle index for a sub-class of restless bandits. We show that a generalization of the adaptive greedy algorithm computes the Whittle index for all indexable restless bandits. We present an efficient implementation of this algorithm which can compute the Whittle index of a restless bandit with K states in 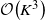$\mathcal{O}\!\left(K^3\right)$ computations. Finally, we present a detailed numerical study which affirms the strong performance of the Whittle index heuristic.

Keywords

Multi-armed banditsrestless banditsWhittle indexindexabilitystochastic schedulingresource allocation

MSC classification

Primary: 90C40: Markov and semi-Markov decision processes
Secondary: 90C39: Dynamic programming 49M20: Methods of relaxation type 91B32: Resource and cost allocation
Type
Original Article
Information
Advances in Applied Probability , Volume 54 , Issue 4 , December 2022 , pp. 1164 - 1192
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abad, C. and Iyengar, G. (2016). A near-optimal maintenance policy for automated DR devices. IEEE Trans. Smart Grid 7, 1411–1419.CrossRefGoogle Scholar
Akbarzadeh, N. and Mahajan, A. (2019). Dynamic spectrum access under partial observations: a restless bandit approach. In Canadian Workshop on Information Theory, Institute of Electrical and Electronics Engineers, Piscataway, NJ, pp. 1–6.Google Scholar
Akbarzadeh, N. and Mahajan, A. (2019). Restless bandits with controlled restarts: indexability and computation of Whittle index. In 58th IEEE Conference on Decision and Control, Institute of Electrical and Electronics Engineers, Piscataway, NJ, pp. 7294–7300.CrossRefGoogle Scholar
Akbarzadeh, N. and Mahajan, A. (2020). An improved algorithm to compute Whittle index. Available at https://codeocean.com/capsule/8680851/tree/v1.Google Scholar
Ansell, P. S., Glazebrook, K. D., Niño-Mora, J. and O’Keeffe, M. (2003). Whittle’s index policy for a multi-class queueing system with convex holding costs. Math. Operat. Res. 57, 21–39.Google Scholar
Archibald, T. W., Black, D. P. and Glazebrook, K. D. (2009). Indexability and index heuristics for a simple class of inventory routing problems. Operat. Res. 57, 314–326.CrossRefGoogle Scholar
Avrachenkov, K., Ayesta, U., Doncel, J. and Jacko, P. (2013). Congestion control of TCP flows in internet routers by means of index policy. Computer Networks 57, 3463–3478.CrossRefGoogle Scholar
Ayesta, U., Erausquin, M. and Jacko, P. (2010). A modeling framework for optimizing the flow-level scheduling with time-varying channels. Performance Evaluation 67, 1014–1029.CrossRefGoogle Scholar
Bertsimas, D. and Niño-Mora, J. (1996). Conservation laws, extended polymatroids and multiarmed bandit problems; a polyhedral approach to indexable systems. Math. Operat. Res. 21, 257–306.CrossRefGoogle Scholar
Chakravorty, J. and Mahajan, A. (2014). Multi-armed bandits, Gittins index, and its calculation. In Methods and Applications of Statistics in Clinical Trials: Planning, Analysis, and Inferential Methods, Vol. 2, John Wiley, Hoboken, NJ, pp. 416–435.Google Scholar
Deo, S. et al. (2013). Improving health outcomes through better capacity allocation in a community-based chronic care model. Operat. Res. 61, 1277–1294.CrossRefGoogle Scholar
Egidi, N. and Maponi, P. (2006). A Sherman–Morrison approach to the solution of linear systems. J. Comput. Appl. Math. 189, 703–718.CrossRefGoogle Scholar
Gittins, J., Glazebrook, K. and Weber, R. (2011). Multi-armed Bandit Allocation Indices. John Wiley, Chichester.CrossRefGoogle Scholar
Gittins, J. C. (1979). Bandit processes and dynamic allocation indices. J. R. Statist. Soc. B 41, 148–177.Google Scholar
Glazebrook, K., Hodge, D. and Kirkbride, C. (2013). Monotone policies and indexability for bidirectional restless bandits. Adv. Appl. Prob. 45, 51–85.CrossRefGoogle Scholar
Glazebrook, K. and Mitchell, H. (2002). An index policy for a stochastic scheduling model with improving/deteriorating jobs. Naval Res. Logistics 49, 706–721.CrossRefGoogle Scholar
Glazebrook, K. D., Kirkbride, C. and Ouenniche, J. (2009). Index policies for the admission control and routing of impatient customers to heterogeneous service stations. Operat. Res. 57, 975–989.CrossRefGoogle Scholar
Glazebrook, K. D., Mitchell, H. M. and Ansell, P. S. (2005). Index policies for the maintenance of a collection of machines by a set of repairmen. Europ. J. Operat. Res. 165, 267–284.CrossRefGoogle Scholar
Glazebrook, K. D., Ruiz-Hernandez, D. and Kirkbride, C. (2006). Some indexable families of restless bandit problems. Adv. Appl. Prob. 38, 643–672.CrossRefGoogle Scholar
Jacko, P. (2012). Optimal index rules for single resource allocation to stochastic dynamic competitors. In VALUETOOLS ’11: Proc. 5th International ICST Conference on Performance Evaluation Methodologies and Tools, Association for Computing Machinery, New York, pp. 425–433.CrossRefGoogle Scholar
Liu, K. and Zhao, Q. (2010). Indexability of restless bandit problems and optimality of Whittle index for dynamic multichannel access. IEEE Trans. Inf. Theory 56, 5547–5567.CrossRefGoogle Scholar
Lott, C. and Teneketzis, D. (2000). On the optimality of an index rule in multichannel allocation for single-hop mobile networks with multiple service classes. Prob. Eng. Inf. Sci. 14, 259–297.CrossRefGoogle Scholar
Niño-Mora, J. (2001). Restless bandits, partial conservation laws and indexability. Adv. Appl. Prob. 33, 76–98.CrossRefGoogle Scholar
Niño-Mora, J. (2002). Dynamic allocation indices for restless projects and queueing admission control: a polyhedral approach. Math. Program. 93, 361–413.CrossRefGoogle Scholar
Niño-Mora, J. (2007). Dynamic priority allocation via restless bandit marginal productivity indices. TOP 15, 161–198.CrossRefGoogle Scholar
Niño-Mora, J. (2006). Restless bandit marginal productivity indices, diminishing returns, and optimal control of make-to-order/make-to-stock M/G/1 queues. Math. Operat. Res. 31, 50–84.Google Scholar
Papadimitriou, C. H. and Tsitsiklis, J. N. (1999). The complexity of optimal queuing network control. Math. Operat. Res. 24, 293–305.CrossRefGoogle Scholar
Puterman, M. L. (2014). Markov Decision Processes: Discrete Stochastic Dynamic Programming. John Wiley, Hoboken, NJ.Google Scholar
Qian, Y., Zhang, C., Krishnamachari, B. and Tambe, M. (2016). Restless poachers: handling exploration–exploitation tradeoffs in security domains. In AAMAS ’16: Proc. 2016 International Conference on Autonomous Agents and Multiagent Systems, Association for Computing Machinery, New York, pp. 123–131.Google Scholar
Wang, J., Ren, X., Mo, Y. and Shi, L. (2020). Whittle index policy for dynamic multichannel allocation in remote state estimation. IEEE Trans. Automatic Control 65, 591–603.CrossRefGoogle Scholar
Weber, R. R. and Weiss, G. (1990). On an index policy for restless bandits. J. Appl. Prob. 27, 637–648.Google Scholar
Whittle, P. (1988). Restless bandits: activity allocation in a changing world. J. Appl. Prob. 25, 287–298.CrossRefGoogle Scholar
Yu, Z., Xu, Y. and Tong, L. (2018). Deadline scheduling as restless bandits. IEEE Trans. Automatic Control 63, 2343–2358.CrossRefGoogle Scholar