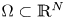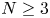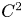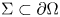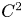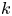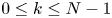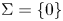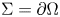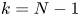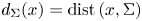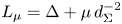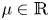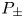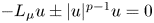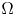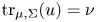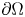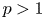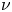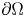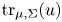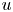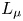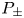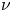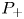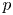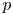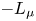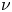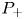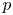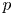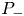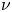Let \Omega \subset \mathbb {R}^N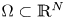$\Omega \subset \mathbb {R}^N$ (N\geq 3$N\geq 3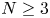$) be a C^2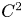$C^2$ bounded domain and \Sigma \subset \partial \Omega$\Sigma \subset \partial \Omega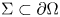$ be a C^2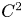$C^2$ compact submanifold without boundary, of dimension k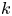$k$, 0\leq k \leq N-1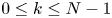$0\leq k \leq N-1$. We assume that \Sigma = \{0\}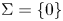$\Sigma = \{0\}$ if k = 0$k = 0$ and \Sigma =\partial \Omega$\Sigma =\partial \Omega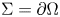$ if k=N-1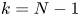$k=N-1$. Let d_{\Sigma }(x)=\mathrm {dist}\,(x,\Sigma )$d_{\Sigma }(x)=\mathrm {dist}\,(x,\Sigma )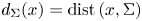$ and L_\mu = \Delta + \mu \,d_{\Sigma }^{-2}$L_\mu = \Delta + \mu \,d_{\Sigma }^{-2}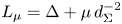$, where \mu \in {\mathbb {R}}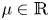$\mu \in {\mathbb {R}}$. 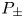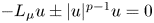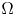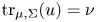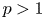We study boundary value problems (P_\pm$P_\pm$) -{L_\mu} u \pm |u|^{p-1}u = 0$-{L_\mu} u \pm |u|^{p-1}u = 0$ in \Omega$\Omega$ and \mathrm {tr}_{\mu,\Sigma}(u)=\nu$\mathrm {tr}_{\mu,\Sigma}(u)=\nu$ on \partial \Omega$\partial \Omega$, where p>1$p>1$, \nu$\nu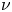$ is a given measure on \partial \Omega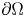$\partial \Omega$ and \mathrm {tr}_{\mu,\Sigma}(u)$\mathrm {tr}_{\mu,\Sigma}(u)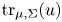$ denotes the boundary trace of u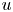$u$ associated to L_\mu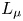$L_\mu$. Different critical exponents for the existence of a solution to (P_\pm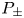$P_\pm$) appear according to concentration of \nu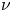$\nu$. The solvability for problem (P_+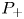$P_+$) was proved in [3, 29] in subcritical ranges for p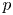$p$, namely for p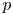$p$ smaller than one of the critical exponents. In this paper, assuming the positivity of the first eigenvalue of -L_\mu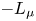$-L_\mu$, we provide conditions on \nu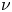$\nu$ expressed in terms of capacities for the existence of a (unique) solution to (P_+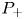$P_+$) in supercritical ranges for p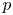$p$, i.e. for p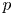$p$ equal or bigger than one of the critical exponents. 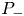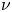We also establish various equivalent criteria for the existence of a solution to (P_-$P_-$) under a smallness assumption on \nu$\nu$.