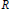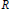Let $R$ be a countable, principal ideal domain which is not a field and $A$ be a countable $R$-algebra which is free as an 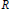$R$-module. Then we will construct an 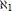${{\aleph }_{1}}$-free 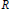$R$-module 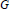$G$ of rank 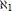${{\aleph }_{1}}$ with endomorphism algebra $\text{En}{{\text{d}}_{R}}\,G=A$. Clearly the result does not hold for fields. Recall that an 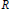$R$-module is 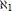${{\aleph }_{1}}$-free if all its countable submodules are free, a condition closely related to Pontryagin’s theorem. This result has many consequences, depending on the algebra $A$ in use. For instance, if we choose 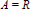$A\,=\,R$, then clearly 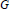$G$ is an indecomposable ‘almost free’module. The existence of such modules was unknown for rings with only finitelymany primes like 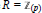$R={{\mathbb{Z}}_{\left( p \right)}}$, the integers localized at some prime $p$. The result complements a classical realization theorem of Corner’s showing that any such algebra is an endomorphism algebra of some torsionfree, reduced 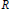$R$-module 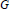$G$ of countable rank. Its proof is based on new combinatorialalgebraic techniques related with what we call rigid tree-elements coming from a module generated over a forest of trees.