Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T03:15:44.134Z Has data issue: false hasContentIssue false
  • English
  • Français

Indecomposable Almost Free Modules—The Local Case

Published online by Cambridge University Press:  20 November 2018

Rüdiger Göbel  and
Saharon Shelah
Rüdiger Göbel*
Affiliation:
Fachbereich 6, Mathematik und Informatik Universität Essen 45117 Essen Germany
Saharon Shelah*
Affiliation:
Department of Mathematics, Hebrew University, Jerusalem, Israel and Rutgers University, New Brunswick, New Jersey, U.S.A.
*
e-mail: [email protected]
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

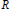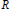Let $R$ be a countable, principal ideal domain which is not a field and $A$ be a countable $R$-algebra which is free as an 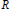$R$-module. Then we will construct an 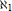${{\aleph }_{1}}$-free 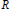$R$-module 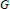$G$ of rank 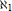${{\aleph }_{1}}$ with endomorphism algebra 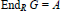$\text{En}{{\text{d}}_{R}}\,G=A$. Clearly the result does not hold for fields. Recall that an 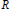$R$-module is 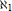${{\aleph }_{1}}$-free if all its countable submodules are free, a condition closely related to Pontryagin’s theorem. This result has many consequences, depending on the algebra $A$ in use. For instance, if we choose 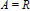$A\,=\,R$, then clearly 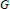$G$ is an indecomposable ‘almost free’module. The existence of such modules was unknown for rings with only finitelymany primes like 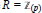$R={{\mathbb{Z}}_{\left( p \right)}}$, the integers localized at some prime $p$. The result complements a classical realization theorem of Corner’s showing that any such algebra is an endomorphism algebra of some torsionfree, reduced 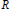$R$-module 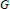$G$ of countable rank. Its proof is based on new combinatorialalgebraic techniques related with what we call rigid tree-elements coming from a module generated over a forest of trees.

Keywords

20K2020K2620K3013C10indecomposable modules of local ringsℵ1-free modules of rank ℵ1realizing rings as endomorphism rings
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 4 , 01 August 1998 , pp. 719 - 738
Copyright
Copyright © Canadian Mathematical Society 1998

Footnotes

This work is supported by the project No. G-0294-081.06/93 of the German-Israeli Foundation for Scientific Research & Development.

No. 591 from Shelah’s list of publications.

References

1. Baer, R., Abelian groups without elements of finite order. Duke Math. J. 3(1937), 68–122.Google Scholar
2. Corner, A. L. S., Every countable reduced torsion-free ring is an endomorphism ring. Proc. London Math. Soc. (3) 13(1963), 687–710.Google Scholar
3. Corner, A. L. S., Additive categories and a theorem of W. G. Leavitt. Bull. Amer. Math. Soc. 75(1969), 78–82.Google Scholar
4. Corner, A. L. S. and Göbel, R., Prescribing endomorphism algebras, a unified treatment. Proc. London Math. Soc. (3) 50(1985), 447–479.Google Scholar
5. Devlin, K. and Shelah, S., A weak version of ⋄ which follows from 2 ℒ 0 Ú 2 ℒ 1 . Israel J. Math. 29(1978), 239–247.Google Scholar
6. Dugas, M., Fast freie abelsche Gruppen mit Endomorphismenringℤ. J. Algebra 71(1981), 314–321.Google Scholar
7. Dugas, M. and Göbel, R., Every cotorsion-free ring is an endomorphism ring. Proc. London Math. Soc (3) 45(1982), 319–336.Google Scholar
8. Dugas, M., Every cotorsion-free algebra is an endomorphism algebra. Math. Z. 181(1982), 451–470.Google Scholar
9. Dugas, M., On radicals and products. Pacific J. Math. 18(1985), 70–104.Google Scholar
10. Eda, K., Cardinal restrictions for preradicals. In: Abelian Group Theory, Contemporary Math. 87, Providence, 1989. 277–283.Google Scholar
11. Eklof, P. C., On the existence ofî-free abelian groups. Proc. Amer. Math. Soc. 47(1975), 65–72.Google Scholar
12. Eklof, P. C., Set theoretic methods in homological algebra and abelian groups. Les Presses de l’Université de Montréal, Montreal, 1980.Google Scholar
13. Eklof, P.C. and A. H.Mekler, On constructing indecomposable groups in L. J. Algebra 49(1977), 96–103.Google Scholar
14. Eklof, P.C., Almost free modules, set-theoretic methods. North-Holland, Amsterdam, 1990.Google Scholar
15. Eklof, P. C. and Shelah, S., On Whitehead modules. J. Algebra 142(1991), 492–510.Google Scholar
16. Fuchs, L., Infinite abelian groups, Vol. I. Academic Press, New York, 1970.Google Scholar
17. Fuchs, L., Infinite abelian groups, Vol.II. Academic Press, New York, 1973.Google Scholar
18. Göbel, R., An easy topological construction for realizing endomorphism rings. Proc. Roy. Irish Acad. Sect. A 92(1992), 281–284.Google Scholar
19. Göbel, R. and May, W., Independence in completions and endomorphism algebras.Math. Forum1(1989), 215-226.Google Scholar
20. Göbel, R. and May, W., Four submodules suffice for realizing algebras over commutative rings. J. Pure Appl. Algebra 65(1990), 29–43.Google Scholar
21. Göbel, R. and Shelah, S., On the existence of rigid ℵ 1-free abelian groups of cardinality ℵ1. In: Abelian Groups and Modules, Proceedings of the Padova Conference 1994, Math. and Its Appl. 343, Kluwer Academic Publ., London, 1995. 277–237.Google Scholar
22. Göbel, R., G.C.H. implies the existence of many rigid almost free abelian groups. In: Abelian Groups and Modules, Proceedings of the international conference at Colorado Springs 1995, Lecture Notes in Pure and Appl. Math. 182, Marcel Dekker, New York, 1996. 253–271.Google Scholar
23. Phillip Griffith, ℵ n-free abelian groups. Quart. J. Math. Oxford Ser. (2) 23(1972), 417–425.Google Scholar
24. Higman, G., Almost free groups. Proc. London Math. Soc. 1(1951), 184–190.Google Scholar
25. Higman, G., Some countably free groups. In: Proceedings Group Theory, W. de Gruyter Publ. Singapore, 1991. 129–150.Google Scholar
26. Hill, P., New criteria for freeness in abelian groups II. Trans. Amer.Math. Soc. 196(1974), 191–201.Google Scholar
27. Jech, T., Set Theory. Academic Press, New York, 1978.Google Scholar
28. Magidor, M. and Shelah, S., When does almost free imply free? (for groups, transversals, etc.). J. Amer. Math. Soc. (4) 7(1994), 769–830.Google Scholar
29. Mekler, A. H., How to construct almost free groups. Canad. J. Math. 32(1980), 1206–1228.Google Scholar
30. Rotman, J., Homological Algebra. Academic Press, New York, 1979.Google Scholar
31. Shelah, S., A compactness theoremfor singular cardinals, free algebras,Whitehead problemand transversals. Israel J. Math. 21(1975), 319–349.Google Scholar
32. Shelah, S., On successors of singular cardinals. Logic Colloquium ‘78 97, Stud. Logic Foundations Math., North Holland, Amsterdam, New York, 1978. 357–380.Google Scholar
33. Shelah, S., On uncountable abelian groups, Israel J. Math. 32(1979), 311–330.Google Scholar
34. Shelah, S., Whitehead groups may not be free, even assumingCH, II. Israel J. Math. 35(1980), 257–285.Google Scholar
35. Shelah, S., On endo-rigid stronglyℵ 1-free abelian groups in ℵ 1. Israel J. Math. 40(1981), 291–295.Google Scholar
36. Shelah, S., A combinatorial principle and endomorphism rings. I: On p-groups. Israel J. Math. 49(1984), 239–257.Google Scholar
37. Shelah, S., A combinatorial theorem and endomorphism rings of abelian groups, II. In: Abelian groups and modules, CISMLecture Notes 287, Springer Wien, New York, 1984. 37–86.Google Scholar
38. Shelah, S., Incompactness in regular cardinals. Notre Dame J. Formal Logic, 26(1985), 195–228.Google Scholar
39. Shelah, S., A note on k-freeness of abelian groups. In: Around classification theory of models, Lecture Notes in Math. 1182, Springer, Berlin, 1986. 260–268.Google Scholar
40. Shelah, S., The number of pairwise non-elementary embeddable models. J. Symbolic Logic, 54(1989), 1431–1455.Google Scholar
41. Shelah, S., Non Structure Theory. Oxford Univ. Press, 1996.Google Scholar
42. Shelah, S. and Spasojevic, Z., A forcing axiom on strongly inaccessible cardinals making all uniformizations for all ladder systems lying on a fixed stationary set and applications for abelian groups. manuscript 587.Google Scholar