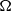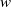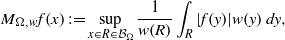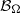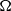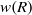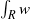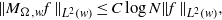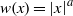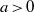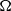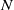1 results
DIRECTIONAL MAXIMAL OPERATORS AND RADIAL WEIGHTS ON THE PLANE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 12 September 2013, pp. 397-414
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
-
Let 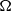\Omega be the set of unit vectors and 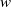w be a radial weight on the plane. We consider the weighted directional maximal operator defined by
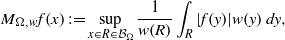\begin{eqnarray*}{M}_{\Omega , w} f(x): = \sup _{x\in R\in \mathcal{B} _{\Omega }}\frac{1}{w(R)} \int \nolimits \nolimits_{R} \vert f(y)\vert w(y)\hspace{0.167em} dy,\end{eqnarray*}where 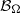{ \mathcal{B} }_{\Omega } denotes the set of all rectangles on the plane whose longest side is parallel to some unit vector in 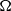\Omega and 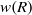w(R) denotes 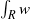\int \nolimits \nolimits_{R} w. In this paper we prove an almost-orthogonality principle for this maximal operator under certain conditions on the weight. The condition allows us to get the weighted norm inequality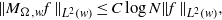\begin{eqnarray*}\Vert {M}_{\Omega , w} f\mathop{\Vert }\nolimits_{{L}^{2} (w)} \leq C\log N\Vert f\mathop{\Vert }\nolimits_{{L}^{2} (w)} ,\end{eqnarray*}when 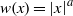w(x)= \vert x\hspace{-1.2pt}\mathop{\vert }\nolimits ^{a} , 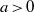a\gt 0, and when 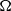\Omega is the set of unit vectors on the plane with cardinality 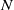N sufficiently large.
