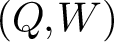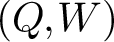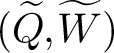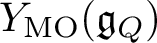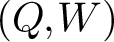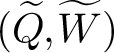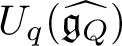Given a quiver with potential 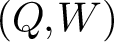$(Q,W)$, Kontsevich–Soibelman constructed a cohomological Hall algebra (CoHA) on the critical cohomology of the stack of representations of 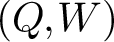$(Q,W)$. Special cases of this construction are related to work of Nakajima, Varagnolo, Schiffmann–Vasserot, Maulik–Okounkov, Yang–Zhao, etc. about geometric constructions of Yangians and their representations; indeed, given a quiver Q, there exists an associated pair 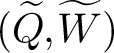$(\widetilde{Q}, \widetilde{W})$ whose CoHA is conjecturally the positive half of the Maulik–Okounkov Yangian 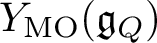$Y_{\text {MO}}(\mathfrak {g}_{Q})$.

For a quiver with potential 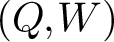$(Q,W)$, we follow a suggestion of Kontsevich–Soibelman and study a categorification of the above algebra constructed using categories of singularities. Its Grothendieck group is a K-theoretic Hall algebra (KHA) for quivers with potential. We construct representations using framed quivers, and we prove a wall-crossing theorem for KHAs. We expect the KHA for 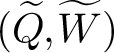$(\widetilde{Q}, \widetilde{W})$ to recover the positive part of quantum affine algebra 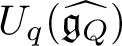$U_{q}(\widehat {\mathfrak {g}_{Q}})$ defined by Okounkov–Smirnov.