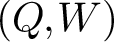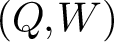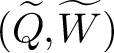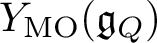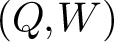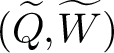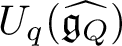1 Introduction
1.1 Quivers with potential
Let Y be a Calabi–Yau
![]() $3$
-fold, and let
$3$
-fold, and let
![]() $\beta \in H^{4}(Y,\mathbb {Z})\oplus H^{6}(Y,\mathbb {Z})$
. The Donaldson–Thomas (DT) invariants of Y are virtual counts of curves on Y of support
$\beta \in H^{4}(Y,\mathbb {Z})\oplus H^{6}(Y,\mathbb {Z})$
. The Donaldson–Thomas (DT) invariants of Y are virtual counts of curves on Y of support
![]() $\beta $
, and they are defined using the geometry of the moduli stack
$\beta $
, and they are defined using the geometry of the moduli stack
![]() $\mathfrak {M}_{\beta }$
of sheaves with compact support
$\mathfrak {M}_{\beta }$
of sheaves with compact support
![]() $\beta $
. One can define DT invariants for quivers with potential
$\beta $
. One can define DT invariants for quivers with potential
![]() $(Q,W)$
using the vanishing cycle sheaf
$(Q,W)$
using the vanishing cycle sheaf
![]() $\varphi _{\text {Tr}\,(W)}\mathbb {Q}$
of the regular function
$\varphi _{\text {Tr}\,(W)}\mathbb {Q}$
of the regular function
on the stack
![]() $\mathcal {X}(d)$
of representation of Q of a given dimension d.
$\mathcal {X}(d)$
of representation of Q of a given dimension d.
For any Calabi–Yau
![]() $3$
-fold
$3$
-fold
![]() $Y,$
the stack
$Y,$
the stack
![]() $\mathfrak {M}_{\beta }$
is locally analytically described by
$\mathfrak {M}_{\beta }$
is locally analytically described by
![]() $\text {crit}\,(\text {Tr}\,(W))\subset \mathcal {X}(d)$
for a quiver with potential
$\text {crit}\,(\text {Tr}\,(W))\subset \mathcal {X}(d)$
for a quiver with potential
![]() $(Q,W)$
[Reference Joyce and Song14], [Reference Toda34], and the DT invariants are defined using the sheaves
$(Q,W)$
[Reference Joyce and Song14], [Reference Toda34], and the DT invariants are defined using the sheaves
![]() $\varphi _{\text {Tr}\,(W)}\mathbb {Q}$
. This description is global for
$\varphi _{\text {Tr}\,(W)}\mathbb {Q}$
. This description is global for
![]() $Y=\mathbb {A}^{3}_{\mathbb {C}}$
and
$Y=\mathbb {A}^{3}_{\mathbb {C}}$
and
![]() $\beta =d\in \mathbb {N}$
. Consider the quiver
$\beta =d\in \mathbb {N}$
. Consider the quiver
![]() $Q_{3}$
with one vertex and three loops
$Q_{3}$
with one vertex and three loops
![]() $x, y$
and z and potential
$x, y$
and z and potential
![]() $W_{3}=xyz-xzy$
. Then
$W_{3}=xyz-xzy$
. Then
It is thus worthwhile to study the DT theory of quivers with potential and try to generalize the constructions and results to the general case of a Calabi–Yau
![]() $3$
-fold.
$3$
-fold.
1.2 Cohomological Hall algebras
Let I be the set of vertices of Q, let
![]() $\theta \in \mathbb {Q}^{I}$
be a generic King stability condition, let
$\theta \in \mathbb {Q}^{I}$
be a generic King stability condition, let
![]() $\mu \in \mathbb {Q}$
a slope, let
$\mu \in \mathbb {Q}$
a slope, let
![]() $\Lambda _{\mu }\subset \mathbb {N}^{I}$
be the subset of dimension vectors of slope
$\Lambda _{\mu }\subset \mathbb {N}^{I}$
be the subset of dimension vectors of slope
![]() $\mu $
and let
$\mu $
and let
![]() $d\in \Lambda _{\mu }$
. Denote by
$d\in \Lambda _{\mu }$
. Denote by
the stack of
![]() $\theta $
-semistable representations of slope
$\theta $
-semistable representations of slope
![]() $\mu $
. The cohomological Hall algebra (CoHA), constructed by Kontsevich–Soibelman [Reference Kontsevich and Soibelman16], is an algebra with underlying
$\mu $
. The cohomological Hall algebra (CoHA), constructed by Kontsevich–Soibelman [Reference Kontsevich and Soibelman16], is an algebra with underlying
![]() $\Lambda _{\mu }$
-graded vector space:
$\Lambda _{\mu }$
-graded vector space:
 $$ \begin{align*}\text{CoHA}\,(Q, W)_{\mu}:=\bigoplus_{d\in \Lambda_{\mu}}H^{\cdot}\left(\mathcal{X}(d)^{\text{ss}}, \varphi_{\text{Tr}\,W}\mathbb{Q}\right),\end{align*} $$
$$ \begin{align*}\text{CoHA}\,(Q, W)_{\mu}:=\bigoplus_{d\in \Lambda_{\mu}}H^{\cdot}\left(\mathcal{X}(d)^{\text{ss}}, \varphi_{\text{Tr}\,W}\mathbb{Q}\right),\end{align*} $$
where the multiplication
![]() $m=p_{*}q^{*}$
is defined using the maps
$m=p_{*}q^{*}$
is defined using the maps
 $$ \begin{align} \mathcal{X}(d)^{\text{ss}}\times \mathcal{X}(e)^{\text{ss}}\xleftarrow{q} \mathcal{X}(d,e)^{\text{ss}}\xrightarrow{p} \mathcal{X}(d+e)^{\text{ss}} \end{align} $$
$$ \begin{align} \mathcal{X}(d)^{\text{ss}}\times \mathcal{X}(e)^{\text{ss}}\xleftarrow{q} \mathcal{X}(d,e)^{\text{ss}}\xrightarrow{p} \mathcal{X}(d+e)^{\text{ss}} \end{align} $$
from the stack
![]() $\mathcal {X}(d,e)$
parametrizing pairs of representations
$\mathcal {X}(d,e)$
parametrizing pairs of representations
![]() $A\subset B$
with A of dimension d and B of dimension
$A\subset B$
with A of dimension d and B of dimension
![]() $d+e$
. Consider the regular function
$d+e$
. Consider the regular function
Assume zero is its only critical value. The critical locus of
![]() $\text {Tr}(W)$
is
$\text {Tr}(W)$
is
![]() $\mathcal {X}(Q,W,d)$
, the moduli of representations of dimension d of the Jacobi algebra
$\mathcal {X}(Q,W,d)$
, the moduli of representations of dimension d of the Jacobi algebra

so the vector space
![]() $H^{\cdot }(\mathcal {X}(d),\varphi _{\text {Tr}\,W}\mathbb {Q})$
is the critical cohomology of the (usually singular) space
$H^{\cdot }(\mathcal {X}(d),\varphi _{\text {Tr}\,W}\mathbb {Q})$
is the critical cohomology of the (usually singular) space
![]() $\mathcal {X}(Q,W,d)$
with coefficients in (a shift of) a perverse sheaf. Using framed quivers, Davison–Meinhardt [Reference Davison and Meinhardt6] and Soibelman [Reference Soibelman32] constructed representations of these algebras.
$\mathcal {X}(Q,W,d)$
with coefficients in (a shift of) a perverse sheaf. Using framed quivers, Davison–Meinhardt [Reference Davison and Meinhardt6] and Soibelman [Reference Soibelman32] constructed representations of these algebras.
For any quiver Q, there is a tripled quiver with potential
 $(\widetilde{Q}, \widetilde{W})$
whose CoHA recovers the preprojective Hall algebra of Q as defined by Schiffmann–Vasserot [Reference Schiffmann and Vasserot31] and Yang–Zhao [Reference Yang and Zhao39]; see [Reference Ren and Soibelman28]. In [Reference Davison4], Davison conjectured that a
$(\widetilde{Q}, \widetilde{W})$
whose CoHA recovers the preprojective Hall algebra of Q as defined by Schiffmann–Vasserot [Reference Schiffmann and Vasserot31] and Yang–Zhao [Reference Yang and Zhao39]; see [Reference Ren and Soibelman28]. In [Reference Davison4], Davison conjectured that a
![]() $\mathbb {C}^{*}$
-equivariant version of
$\mathbb {C}^{*}$
-equivariant version of
 $\text {CoHA}(\widetilde{Q}, \widetilde{W})$
is the positive half of the Maulik–Okounkov Yangian
$\text {CoHA}(\widetilde{Q}, \widetilde{W})$
is the positive half of the Maulik–Okounkov Yangian
![]() $Y_{\text {MO}}$
.
$Y_{\text {MO}}$
.
1.3 Categorical and K-theoretic Hall algebras
In [Reference Kontsevich and Soibelman16, Section 8.1], Kontsevich–Soibelman propose the category of singularities

as a categorification of the critical cohomology
![]() $H^{\cdot }(\mathcal {X}(d), \varphi _{\text {Tr}\,W}\mathbb {Q})$
; see Efimov’s work [Reference Efimov7]. The category of singularities is equivalent to the category of matrix factorizations
$H^{\cdot }(\mathcal {X}(d), \varphi _{\text {Tr}\,W}\mathbb {Q})$
; see Efimov’s work [Reference Efimov7]. The category of singularities is equivalent to the category of matrix factorizations
![]() $\text {MF}(\mathcal {X}(d), W)$
for the regular function
$\text {MF}(\mathcal {X}(d), W)$
for the regular function
![]() $\text {Tr}\,W$
.
$\text {Tr}\,W$
.
Consider the torus
![]() $(\mathbb {C}^{*})^{E}$
whose factor corresponding to
$(\mathbb {C}^{*})^{E}$
whose factor corresponding to
![]() $e\in E$
acts on
$e\in E$
acts on
![]() $R(d)$
by scaling the linear map corresponding to e. Let
$R(d)$
by scaling the linear map corresponding to e. Let
![]() $T\subset (\mathbb {C}^{*})^{E}$
be a torus under which W is invariant. We use the notations introduced in Subsection 1.2.
$T\subset (\mathbb {C}^{*})^{E}$
be a torus under which W is invariant. We use the notations introduced in Subsection 1.2.
Theorem 1.1. Consider the
![]() $\Lambda _{\mu }$
-graded category
$\Lambda _{\mu }$
-graded category
 $$ \begin{align*}\text{HA}_{T}(Q,W)_{\mu}:=\bigoplus_{d\in\Lambda_{\mu}} D_{\text{sg}, T}\left(\mathcal{X}(d)^{\text{ss}}_{0}\right).\end{align*} $$
$$ \begin{align*}\text{HA}_{T}(Q,W)_{\mu}:=\bigoplus_{d\in\Lambda_{\mu}} D_{\text{sg}, T}\left(\mathcal{X}(d)^{\text{ss}}_{0}\right).\end{align*} $$
Then
![]() $\text {HA}_{T}(Q,W)_{\mu }$
is monoidal with multiplication
$\text {HA}_{T}(Q,W)_{\mu }$
is monoidal with multiplication
![]() $m:=p_{*}q^{*}$
, where p and q are the maps in (1). The underlying category is called the categorical Hall algebra (HA) of
$m:=p_{*}q^{*}$
, where p and q are the maps in (1). The underlying category is called the categorical Hall algebra (HA) of
![]() $(Q,W)$
. The Grothendieck group is called the K-theoretic Hall algebra (KHA) of
$(Q,W)$
. The Grothendieck group is called the K-theoretic Hall algebra (KHA) of
![]() $(Q,W)$
.
$(Q,W)$
.
In analogy to cohomology, we may call
![]() $K_{0}\left (D_{\text {sg}}\left (\mathcal {X}(d)_{0}\right )\right )$
the critical K-theory of
$K_{0}\left (D_{\text {sg}}\left (\mathcal {X}(d)_{0}\right )\right )$
the critical K-theory of
![]() $\mathcal {X}(Q,W,d)$
and may denote it by
$\mathcal {X}(Q,W,d)$
and may denote it by
![]() $K_{\text {crit}}\left (\mathcal {X}(Q,W,d)\right )$
. We denote the full Hall algebra (for the zero stability condition) by
$K_{\text {crit}}\left (\mathcal {X}(Q,W,d)\right )$
. We denote the full Hall algebra (for the zero stability condition) by
![]() $\text {HA}_{T}(Q,W)$
and
$\text {HA}_{T}(Q,W)$
and
![]() $\text {KHA}_{T}(Q,W)$
.
$\text {KHA}_{T}(Q,W)$
.
Assume that there is a
![]() $\mathbb {C}^{*}\subset (\mathbb {C}^{*})^{E}$
such that
$\mathbb {C}^{*}\subset (\mathbb {C}^{*})^{E}$
such that
![]() $\text {Tr}\,W_{d}$
has weight
$\text {Tr}\,W_{d}$
has weight
![]() $2$
with respect to
$2$
with respect to
![]() $\mathbb {C}^{*}$
for any
$\mathbb {C}^{*}$
for any
![]() $d\in \mathbb {N}^{I}$
. Then one can consider graded matrix factorization categories
$d\in \mathbb {N}^{I}$
. Then one can consider graded matrix factorization categories
![]() $\text {MF}^{\text {gr}}(\mathcal {X}(d), W)$
which are equivalent to categories of graded singularities
$\text {MF}^{\text {gr}}(\mathcal {X}(d), W)$
which are equivalent to categories of graded singularities
![]() $D_{\text {sg}}^{\text {gr}}\left (\mathcal {X}(d)^{\text {ss}}_{0}\right )$
. One can define a graded version of HA with underlying
$D_{\text {sg}}^{\text {gr}}\left (\mathcal {X}(d)^{\text {ss}}_{0}\right )$
. One can define a graded version of HA with underlying
![]() $\Lambda _{\mu }$
-graded category
$\Lambda _{\mu }$
-graded category
 $$ \begin{align*}\text{HA}^{\text{gr}}_{T}(Q,W)_{\mu}:=\bigoplus_{d\in\Lambda_{\mu}} D^{\text{gr}}_{\text{sg}, T}\left(\mathcal{X}(d)^{\text{ss}}_{0}\right)\end{align*} $$
$$ \begin{align*}\text{HA}^{\text{gr}}_{T}(Q,W)_{\mu}:=\bigoplus_{d\in\Lambda_{\mu}} D^{\text{gr}}_{\text{sg}, T}\left(\mathcal{X}(d)^{\text{ss}}_{0}\right)\end{align*} $$
and multiplication
![]() $m:=p_{*}q^{*}$
. Its Grothendieck group is called
$m:=p_{*}q^{*}$
. Its Grothendieck group is called
![]() $\text {KHA}^{\text {gr}}$
.
$\text {KHA}^{\text {gr}}$
.
1.4 Preprojective Hall algebras
Let Q be a quiver, and consider the tripled quiver
 $(\widetilde{Q}, \widetilde{W})$
. Consider the preprojective Hall algebra defined by Varagnolo–Vasserot:
$(\widetilde{Q}, \widetilde{W})$
. Consider the preprojective Hall algebra defined by Varagnolo–Vasserot:
 $$ \begin{align*}\text{HA}_{T}(Q):=\bigoplus_{d\in\mathbb{N}^{I}} D^{b}_{T}\left(\mathfrak{P}(d)\right),\end{align*} $$
$$ \begin{align*}\text{HA}_{T}(Q):=\bigoplus_{d\in\mathbb{N}^{I}} D^{b}_{T}\left(\mathfrak{P}(d)\right),\end{align*} $$
where
![]() $\mathfrak {P}(d)$
is the stack of representations of dimension d of the preprojective algebra of Q. Using Isik’s equivalence [Reference Isik13], there is an equivalence of underlying categories
$\mathfrak {P}(d)$
is the stack of representations of dimension d of the preprojective algebra of Q. Using Isik’s equivalence [Reference Isik13], there is an equivalence of underlying categories
 $$ \begin{align*}\text{HA}^{\text{gr}}_{T}(\widetilde{Q}, \widetilde{W})\cong \text{HA}_{T}(Q),\end{align*} $$
$$ \begin{align*}\text{HA}^{\text{gr}}_{T}(\widetilde{Q}, \widetilde{W})\cong \text{HA}_{T}(Q),\end{align*} $$
where
![]() $\text {HA}^{\text {gr}}$
is defined using a natural
$\text {HA}^{\text {gr}}$
is defined using a natural
 $\mathbb {C}^{*}\subset (\mathbb {C}^{*})^{\widetilde {E}}$
such that
$\mathbb {C}^{*}\subset (\mathbb {C}^{*})^{\widetilde {E}}$
such that
![]() $\text {Tr}\,\widetilde {W}_{d}$
is homogeneous of weight
$\text {Tr}\,\widetilde {W}_{d}$
is homogeneous of weight
![]() $2$
for any
$2$
for any
![]() $d\in \mathbb {N}^{I}$
. The multiplications differ by conjugation by an equivariant parameter; see [Reference Varagnolo and Vasserot38] and Subsection 3.2.3. Using [Reference Toda36, Corollary 3.13], the categories
$d\in \mathbb {N}^{I}$
. The multiplications differ by conjugation by an equivariant parameter; see [Reference Varagnolo and Vasserot38] and Subsection 3.2.3. Using [Reference Toda36, Corollary 3.13], the categories
![]() $\text {MF}_{T}(\mathcal {X}(d), W)$
and
$\text {MF}_{T}(\mathcal {X}(d), W)$
and
![]() $\text {MF}^{\text {gr}}_{T}(\mathcal {X}(d), W)$
have the same Grothendieck group, so there is an isomorphism
$\text {MF}^{\text {gr}}_{T}(\mathcal {X}(d), W)$
have the same Grothendieck group, so there is an isomorphism
 $$ \begin{align} \text{KHA}^{\text{gr}}_{T}(\widetilde{Q}, \widetilde{W})\cong \text{KHA}_{T}(\widetilde{Q}, \widetilde{W}).\end{align} $$
$$ \begin{align} \text{KHA}^{\text{gr}}_{T}(\widetilde{Q}, \widetilde{W})\cong \text{KHA}_{T}(\widetilde{Q}, \widetilde{W}).\end{align} $$
1.5 Representations of the KHA
There are representations of
![]() $\text {KHA}_{T}(Q,W)_{\mu }$
on critical K-theory spaces associated to moduli of framed representations
$\text {KHA}_{T}(Q,W)_{\mu }$
on critical K-theory spaces associated to moduli of framed representations
 $$ \begin{align*}\bigoplus_{d\in\Lambda_{\mu}} K_{0}^{T}\left(D_{\text{sg}}\left(\mathcal{X}(f,d)^{\text{ss}}_{0}\right)\right).\end{align*} $$
$$ \begin{align*}\bigoplus_{d\in\Lambda_{\mu}} K_{0}^{T}\left(D_{\text{sg}}\left(\mathcal{X}(f,d)^{\text{ss}}_{0}\right)\right).\end{align*} $$
There are analogous representations of
![]() $\text {KHA}^{\text {gr}}_{T}(Q,W)_{\mu }$
. These representations are analogous to the ones constructed in [Reference Davison and Meinhardt6], [Reference Soibelman32] in cohomology.
$\text {KHA}^{\text {gr}}_{T}(Q,W)_{\mu }$
. These representations are analogous to the ones constructed in [Reference Davison and Meinhardt6], [Reference Soibelman32] in cohomology.
Further, for a quiver Q, there are representations of
 $\text {KHA}_{T}^{\text {gr}}(\widetilde{Q}, \widetilde{W})\cong \text {KHA}_{T}(Q)$
on the K-theory of Nakajima quiver varieties
$\text {KHA}_{T}^{\text {gr}}(\widetilde{Q}, \widetilde{W})\cong \text {KHA}_{T}(Q)$
on the K-theory of Nakajima quiver varieties
 $$ \begin{align*}\bigoplus_{d\in\mathbb{N}^{I}} K_{0}^{T}\left(N(f,d)\right).\end{align*} $$
$$ \begin{align*}\bigoplus_{d\in\mathbb{N}^{I}} K_{0}^{T}\left(N(f,d)\right).\end{align*} $$
Quantum affine algebras also naturally act on Nakajima quiver varieties [Reference Nakajima18]. Analogous to Davison’s conjecture [Reference Davison4], we expect preprojective KHAs to be related to positive parts of quantum affine algebras.
Conjecture 1.2. Consider the torus
![]() $\mathbb {C}^{*}$
scaling the linear maps corresponding to edges of the doubled quiver
$\mathbb {C}^{*}$
scaling the linear maps corresponding to edges of the doubled quiver
![]() $Q^{d}$
with weight
$Q^{d}$
with weight
![]() $1$
and scaling the linear maps corresponding to edges of the loops
$1$
and scaling the linear maps corresponding to edges of the loops
![]() $\omega _{i}$
with weight
$\omega _{i}$
with weight
![]() $-2$
; see Subsection 2.4 for the definitions of the doubled quiver
$-2$
; see Subsection 2.4 for the definitions of the doubled quiver
![]() $Q^{d}$
and of the tripled quiver
$Q^{d}$
and of the tripled quiver
![]() $\widetilde{Q}$
. After possibly tensoring with
$\widetilde{Q}$
. After possibly tensoring with
![]() $\mathbb {C}(q)\cong \left (\text {Frac}\,K_{0}(B\mathbb {C}^{*})\right )\otimes \mathbb {C}$
, there is an isomorphism
$\mathbb {C}(q)\cong \left (\text {Frac}\,K_{0}(B\mathbb {C}^{*})\right )\otimes \mathbb {C}$
, there is an isomorphism
 $$ \begin{align*}\text{KHA}_{\mathbb{C}^{*}}\left(Q\right)\cong U^{>}_{q}\left(\widehat{\mathfrak{g}_{Q}}\right),\end{align*} $$
$$ \begin{align*}\text{KHA}_{\mathbb{C}^{*}}\left(Q\right)\cong U^{>}_{q}\left(\widehat{\mathfrak{g}_{Q}}\right),\end{align*} $$
where the right-hand side is the positive part of Okounkov–Smirnov affine quantum algebra [Reference Maulik and Okounkov17], [Reference Orlov22].
The conjecture is true for finite and affine type quivers except
 $A_{1}^{(1)}$
; see [Reference Varagnolo and Vasserot38]. In these cases,
$A_{1}^{(1)}$
; see [Reference Varagnolo and Vasserot38]. In these cases,
![]() $\mathfrak {g}_{Q}$
is the Kac–Moody algebra of Q, but for general quivers Q, the Lie algebra
$\mathfrak {g}_{Q}$
is the Kac–Moody algebra of Q, but for general quivers Q, the Lie algebra
![]() $\mathfrak {g}_{Q}$
is strictly larger than the Kac–Moody algebra of Q.
$\mathfrak {g}_{Q}$
is strictly larger than the Kac–Moody algebra of Q.
1.6 The Jordan quiver
For the Jordan quiver Q with one vertex and one loop, the tripled quiver
![]() $\widetilde{Q}$
has one vertex, three loops and potential
$\widetilde{Q}$
has one vertex, three loops and potential
 $\widetilde {W}=xyz-xzy.$
Let
$\widetilde {W}=xyz-xzy.$
Let
![]() $T\subset (\mathbb {C}^{*})^{3}$
be a torus which fixes W. Consider the action of
$T\subset (\mathbb {C}^{*})^{3}$
be a torus which fixes W. Consider the action of
![]() $\mathbb {C}^{*}$
which scales the linear map corresponding to z with weight
$\mathbb {C}^{*}$
which scales the linear map corresponding to z with weight
![]() $2$
. We consider graded matrix factorization with respect to
$2$
. We consider graded matrix factorization with respect to
![]() $\mathbb {C}^{*}$
. By Isik’s theorem [Reference Isik13], there is an equivalence
$\mathbb {C}^{*}$
. By Isik’s theorem [Reference Isik13], there is an equivalence
 $$ \begin{align*}\text{HA}_{T}^{\text{gr}}(\widetilde{Q}, \widetilde{W})\cong \bigoplus_{d\geqslant 0} D^{b}_{T}\left(\mathfrak{C}(d)\right),\end{align*} $$
$$ \begin{align*}\text{HA}_{T}^{\text{gr}}(\widetilde{Q}, \widetilde{W})\cong \bigoplus_{d\geqslant 0} D^{b}_{T}\left(\mathfrak{C}(d)\right),\end{align*} $$
where
![]() $\mathfrak {C}(d)$
is the stack of commuting matrices of dimension d and the right-hand side has an algebra structure defined by correspondences [Reference Varagnolo and Vasserot38], [Reference Schiffmann and Vasserot30]. The framed representations of the
$\mathfrak {C}(d)$
is the stack of commuting matrices of dimension d and the right-hand side has an algebra structure defined by correspondences [Reference Varagnolo and Vasserot38], [Reference Schiffmann and Vasserot30]. The framed representations of the
 $\text {KHA}_{T}(\widetilde{Q}, \widetilde{W})$
from Subsection 1.5 for the vector
$\text {KHA}_{T}(\widetilde{Q}, \widetilde{W})$
from Subsection 1.5 for the vector
![]() $f=1$
are
$f=1$
are
 $$ \begin{align*}\bigoplus_{d\geqslant 0} K_{\text{crit}}^{T}\left(\text{Hilb}\left(\mathbb{A}^{3}_{\mathbb{C}},d\right)\right).\end{align*} $$
$$ \begin{align*}\bigoplus_{d\geqslant 0} K_{\text{crit}}^{T}\left(\text{Hilb}\left(\mathbb{A}^{3}_{\mathbb{C}},d\right)\right).\end{align*} $$
Further, one constructs representations of
 $\text {KHA}_{T}(\widetilde{Q}, \widetilde{W})$
on the vector space
$\text {KHA}_{T}(\widetilde{Q}, \widetilde{W})$
on the vector space
 $$ \begin{align} \bigoplus_{d\geqslant 0}K_{0}^{T}\left(\text{Hilb}\left(\mathbb{A}^{2}_{\mathbb{C}},d\right)\right). \end{align} $$
$$ \begin{align} \bigoplus_{d\geqslant 0}K_{0}^{T}\left(\text{Hilb}\left(\mathbb{A}^{2}_{\mathbb{C}},d\right)\right). \end{align} $$
Schiffmann–Vasserot [Reference Schiffmann and Vasserot30] and Feigin–Tsymbaliuk [Reference Feigin and Tsymbaliuk8] construct representations of
 $U_{q, t}(\widehat {\widehat {\mathfrak {gl}_{1}}})$
, the Drinfeld double of a subalgebra of
$U_{q, t}(\widehat {\widehat {\mathfrak {gl}_{1}}})$
, the Drinfeld double of a subalgebra of
 $\text {KHA}_{T}(\widetilde{Q}, \widetilde{W})$
, on the vector space (3).
$\text {KHA}_{T}(\widetilde{Q}, \widetilde{W})$
, on the vector space (3).
1.7 Wall-crossing
The CoHA satisfies a wall-crossing theorem by work of Davison–Meinhardt [Reference Davison and Meinhardt6]. We prove an analogous result for KHAs of quivers with potential which satisfy a Künneth-type assumption (see Subsection 5.1.3):
 $$ \begin{align*}\text{KHA}(Q,W)\xrightarrow{\sim} \bigotimes_{\mu\in\mathbb{Q}} \text{KHA}(Q,W)_{\mu}.\end{align*} $$
$$ \begin{align*}\text{KHA}(Q,W)\xrightarrow{\sim} \bigotimes_{\mu\in\mathbb{Q}} \text{KHA}(Q,W)_{\mu}.\end{align*} $$
It is an advantage that we can formulate an analogous categorical statement because by general principles it suffices to check the categorical statement for the zero potential. In this case, the statement follows from work of Halpern–Leistner [Reference Halpern-Leistner11] and Ballard–Favero–Katzarkov [Reference Ballard, Favero and Katzarkov2] on semiorthogonal decompositions in GIT.
1.8 Further properties of the KHA
There is a PBW theorem for CoHAs [Reference Davison and Meinhardt6] for all symmetric quivers Q with potential. For KHAs, we expect such a theorem for
 $(\widetilde{Q}, \widetilde{W})$
by Conjecture 1.2. In [Reference Pădurariu23, Section 7], we prove a PBW theorem for KHAs for all pairs
$(\widetilde{Q}, \widetilde{W})$
by Conjecture 1.2. In [Reference Pădurariu23, Section 7], we prove a PBW theorem for KHAs for all pairs
![]() $(Q,W)$
with Q symmetric.
$(Q,W)$
with Q symmetric.
In [Reference Pădurariu24], inspired by explicit computations of KHAs due to Neguţ [Reference Neguţ19], [Reference Neguţ20], we construct a Drinfeld double Hopf algebra of KHAs for a class of quivers with potential
![]() $(Q,W)$
satisfying a Künneth-type assumption. This class includes all tripled quivers
$(Q,W)$
satisfying a Künneth-type assumption. This class includes all tripled quivers
 $(\widetilde{Q}, \widetilde{W})$
.
$(\widetilde{Q}, \widetilde{W})$
.
1.9 Outline of the paper
In Section 2, we review notions about quivers with potential, semiorthogonal decompositions, categories of singularities and matrix factorizations. In Section 3, we prove Theorem 1.1 and discuss some examples of KHAs. In Section 4, we construct the representations of the KHA mentioned in Subsection 1.5. In Section 5, we prove wall-crossing theorems for categorical and K-theoretic HAs.
1.10 Notations and conventions
All the schemes and stacks considered are over
![]() $\mathbb {C}$
. Let X be a scheme or stack. We denote by
$\mathbb {C}$
. Let X be a scheme or stack. We denote by
![]() $D^{b}(X)$
the derived category of coherent sheaves, by
$D^{b}(X)$
the derived category of coherent sheaves, by
![]() $\text {Perf}(X)\subset D^{b}(X)$
its subcategory of perfect complexes and by
$\text {Perf}(X)\subset D^{b}(X)$
its subcategory of perfect complexes and by
![]() $D_{\text {sg}}(X)$
the category of singularities. All functors considered, such as pullback and pushforward, are derived. We denote by
$D_{\text {sg}}(X)$
the category of singularities. All functors considered, such as pullback and pushforward, are derived. We denote by
![]() $K_{i}(X)$
the K-theory of the category
$K_{i}(X)$
the K-theory of the category
![]() $\text {Perf}(X)$
and by
$\text {Perf}(X)$
and by
![]() $G_{i}(X)$
the K-theory of the category
$G_{i}(X)$
the K-theory of the category
![]() $D^{b}(X)$
. For a regular immersion
$D^{b}(X)$
. For a regular immersion
![]() $\iota :\mathcal {X}\hookrightarrow \mathcal {X}^{\prime }$
, denote by
$\iota :\mathcal {X}\hookrightarrow \mathcal {X}^{\prime }$
, denote by
![]() $N_{\iota }$
the normal bundle of
$N_{\iota }$
the normal bundle of
![]() $\mathcal {X}$
in
$\mathcal {X}$
in
![]() $\mathcal {X}^{\prime }$
. For the purposes of this paper, a smooth quotient stack will have the form
$\mathcal {X}^{\prime }$
. For the purposes of this paper, a smooth quotient stack will have the form
where A is a (quasi-)affine smooth variety and G is a reductive group.
The categories considered are dg, and we denote by
![]() $\otimes $
the product of dg categories [Reference Keller15, Subsections 2.2 and 2.3].
$\otimes $
the product of dg categories [Reference Keller15, Subsections 2.2 and 2.3].
We assume that the quivers with potential
![]() $(Q,W)$
considered are such that the regular functions
$(Q,W)$
considered are such that the regular functions
![]() $\text {Tr}\,W: \mathcal {X}(d)\to \mathbb {A}^{1}_{\mathbb {C}}$
have zero as the only critical value. We denote by
$\text {Tr}\,W: \mathcal {X}(d)\to \mathbb {A}^{1}_{\mathbb {C}}$
have zero as the only critical value. We denote by
![]() $\text {MF}(\mathcal {X}(d), W)$
the category of matrix factorizations for the regular function
$\text {MF}(\mathcal {X}(d), W)$
the category of matrix factorizations for the regular function
![]() $\text {Tr}\,W$
. The zero fiber
$\text {Tr}\,W$
. The zero fiber
![]() $\mathcal {X}(d)_{0}$
of
$\mathcal {X}(d)_{0}$
of
![]() $\text {Tr}\,W$
is derived.
$\text {Tr}\,W$
is derived.
2 Background material
2.1 Quivers with potential
Let
![]() $Q=(I, E, s, t)$
be a quiver with vertex set I, edge set E and source and target maps
$Q=(I, E, s, t)$
be a quiver with vertex set I, edge set E and source and target maps
![]() $s, t: E\to I$
. Let
$s, t: E\to I$
. Let
 $d=\left (d^{i}\right )_{i\in I}\in \mathbb {N}^{I}$
be a dimension vector of Q. Consider vector spaces
$d=\left (d^{i}\right )_{i\in I}\in \mathbb {N}^{I}$
be a dimension vector of Q. Consider vector spaces
![]() $V^{i}$
of dimension
$V^{i}$
of dimension
![]() $d^{i}$
. Consider the reductive group
$d^{i}$
. Consider the reductive group
![]() $G(d)$
and its representation
$G(d)$
and its representation
![]() $R(d)$
:
$R(d)$
:
 $$ \begin{align*} G(d)&:=\prod_{I\in I} GL\left(V^{i}\right),\\[3pt] R(d)&:=\prod_{e\in E} \text{Hom}\,(V^{s(e)}, V^{t(e)}). \end{align*} $$
$$ \begin{align*} G(d)&:=\prod_{I\in I} GL\left(V^{i}\right),\\[3pt] R(d)&:=\prod_{e\in E} \text{Hom}\,(V^{s(e)}, V^{t(e)}). \end{align*} $$
Define the quotient stack of representation of Q of dimension d:
A potential W is a linear combination of cycles in Q. A potential determines a regular function:
We will assume throughout the paper that
![]() $0$
is the only critical value. The critical locus of this function is the moduli of representations of the Jacobi algebra
$0$
is the only critical value. The critical locus of this function is the moduli of representations of the Jacobi algebra
, where
![]() $\mathbb {C}Q$
is the path algebra of Q and
$\mathbb {C}Q$
is the path algebra of Q and
![]() $\mathcal {J}$
is the two-sided ideal in
$\mathcal {J}$
is the two-sided ideal in
![]() $\mathbb {C}Q$
generated by the derivatives
$\mathbb {C}Q$
generated by the derivatives
 $\frac {\partial W}{\partial e}$
of W along all edges
$\frac {\partial W}{\partial e}$
of W along all edges
![]() $e\in E$
.
$e\in E$
.
2.2 King stability conditions
Given a tuple
![]() $\theta =(\theta ^{i})_{i\in I}\in \mathbb {Q}^{I}$
, we define the slope function on a dimension vector
$\theta =(\theta ^{i})_{i\in I}\in \mathbb {Q}^{I}$
, we define the slope function on a dimension vector
![]() $d\in \mathbb {N}^{I}\setminus \{0\}$
by
$d\in \mathbb {N}^{I}\setminus \{0\}$
by
 $$ \begin{align*}\tau(d):=\frac{\sum_{i\in I}\theta^{i}d^{i}}{\sum_{i\in I}d^{i}}\in\mathbb{Q}.\end{align*} $$
$$ \begin{align*}\tau(d):=\frac{\sum_{i\in I}\theta^{i}d^{i}}{\sum_{i\in I}d^{i}}\in\mathbb{Q}.\end{align*} $$
For a slope
![]() $\mu \in \mathbb {Q}$
, let
$\mu \in \mathbb {Q}$
, let
![]() $\Lambda _{\mu }\subset \mathbb {N}^{I}$
be the monoid of dimension vectors d with
$\Lambda _{\mu }\subset \mathbb {N}^{I}$
be the monoid of dimension vectors d with
![]() $\tau (d)=\mu $
together with
$\tau (d)=\mu $
together with
![]() $d=0$
. Call a representation V of Q (
$d=0$
. Call a representation V of Q (
![]() $\theta $
-)(semi)stable if, for every proper subrepresentation
$\theta $
-)(semi)stable if, for every proper subrepresentation
![]() $W\subset V$
, we have that
$W\subset V$
, we have that
The locus of stable representations
![]() $R(d)^{\text {s}}$
and semistable representations
$R(d)^{\text {s}}$
and semistable representations
![]() $R(d)^{\text {ss}}$
inside
$R(d)^{\text {ss}}$
inside
![]() $R(d)$
are open. We consider the moduli stack
$R(d)$
are open. We consider the moduli stack
of semistable representations of dimension d.
2.3 Moduli of framed representations
Fix a framing vector
![]() $f\in \mathbb {N}^{I}$
. We define a new quiver
$f\in \mathbb {N}^{I}$
. We define a new quiver
![]() $Q^{f}=(I^{f}, E^{f})$
with
$Q^{f}=(I^{f}, E^{f})$
with
![]() $I^{f}=I\sqcup \{\infty \}$
, and
$I^{f}=I\sqcup \{\infty \}$
, and
![]() $E^{f}$
contains E and
$E^{f}$
contains E and
![]() $f^{i}$
edges from
$f^{i}$
edges from
![]() $\infty $
to the vertex
$\infty $
to the vertex
![]() $i\in I$
. The dimension vector
$i\in I$
. The dimension vector
![]() $d\in \mathbb {N}^{I}$
can be extended to a dimension vector for the new quiver
$d\in \mathbb {N}^{I}$
can be extended to a dimension vector for the new quiver
 $$ \begin{align*}\widetilde{d}:=(1,d)\in\mathbb{N}^{I^{f}}=\mathbb{N}\times \mathbb{N}^{I}.\end{align*} $$
$$ \begin{align*}\widetilde{d}:=(1,d)\in\mathbb{N}^{I^{f}}=\mathbb{N}\times \mathbb{N}^{I}.\end{align*} $$
Fix a slope
![]() $\mu \in \mathbb {Q}$
. Define
$\mu \in \mathbb {Q}$
. Define
![]() $\theta ^{\prime }=\mu +\varepsilon $
for a small positive rational number
$\theta ^{\prime }=\mu +\varepsilon $
for a small positive rational number
![]() $\varepsilon>0$
. The stability condition
$\varepsilon>0$
. The stability condition
![]() $\theta $
is extended to a stability condition for the quiver
$\theta $
is extended to a stability condition for the quiver
![]() $Q^{f}$
:
$Q^{f}$
:
 $$ \begin{align*}\theta^{f}:=(\theta^{\prime}, \theta)\in \mathbb{Q}^{I^{f}}.\end{align*} $$
$$ \begin{align*}\theta^{f}:=(\theta^{\prime}, \theta)\in \mathbb{Q}^{I^{f}}.\end{align*} $$
2.4 The tripled quiver
The following construction was introduced by Ginzburg [Reference Ginzburg9], and it is used in conjunction with dimensional reduction to obtain representations of a preprojective CoHA or KHA on the cohomology or K-theory of Nakajima quiver varieties.
Let
![]() $Q=(I,E)$
be a quiver. For an edge e, let
$Q=(I,E)$
be a quiver. For an edge e, let
![]() $\overline {e}$
be the edge of opposite orientation. Let
$\overline {e}$
be the edge of opposite orientation. Let
![]() $\overline {E}:=\{\overline {e}|\,e\in E\}$
. The double quiver
$\overline {E}:=\{\overline {e}|\,e\in E\}$
. The double quiver
![]() $Q^{d}=(I, E^{d})$
has edge set
$Q^{d}=(I, E^{d})$
has edge set
![]() $E^{d}:=E\cup \overline {E}$
. For every
$E^{d}:=E\cup \overline {E}$
. For every
![]() $i\in I$
, denote by
$i\in I$
, denote by
![]() $\omega _{i}$
a loop at i. The tripled quiver
$\omega _{i}$
a loop at i. The tripled quiver
 $\widetilde {Q}=(I, \widetilde {E})$
has vertex set I and
$\widetilde {Q}=(I, \widetilde {E})$
has vertex set I and
 $\widetilde {E}=E^{d}\sqcup \{\omega _{i}|\,i\in I\}.$
The potential
$\widetilde {E}=E^{d}\sqcup \{\omega _{i}|\,i\in I\}.$
The potential
![]() $\widetilde {W}$
is defined by
$\widetilde {W}$
is defined by
 $$ \begin{align*}\widetilde{W}:=\sum_{e\in E} \omega_{s(e)}[\bar{e}, e].\end{align*} $$
$$ \begin{align*}\widetilde{W}:=\sum_{e\in E} \omega_{s(e)}[\bar{e}, e].\end{align*} $$
2.5 Nakajima quiver varieties
Let Q be a quiver,
![]() $d\in \mathbb {N}^{I}$
a dimension vector,
$d\in \mathbb {N}^{I}$
a dimension vector,
![]() $\theta \in \mathbb {Q}^{I}$
a stability condition,
$\theta \in \mathbb {Q}^{I}$
a stability condition,
![]() $\mu \in \mathbb {Q}$
and
$\mu \in \mathbb {Q}$
and
![]() $f\in \mathbb {N}^{I}$
a framing vector. Extend
$f\in \mathbb {N}^{I}$
a framing vector. Extend
![]() $\theta $
to the stability condition
$\theta $
to the stability condition
![]() $\theta ^{f}$
for
$\theta ^{f}$
for
![]() $Q^{f}$
as in Subsection 2.3. Associated to
$Q^{f}$
as in Subsection 2.3. Associated to
![]() $\theta $
, there is a character
$\theta $
, there is a character
 $$ \begin{align*}\chi_{\theta}:=\prod_{i\in I} \det(g^{i})^{m\theta^{i}}: G(d)\to\mathbb{C}^{*}\end{align*} $$
$$ \begin{align*}\chi_{\theta}:=\prod_{i\in I} \det(g^{i})^{m\theta^{i}}: G(d)\to\mathbb{C}^{*}\end{align*} $$
for m a positive integer such that
![]() $m\theta ^{i}$
are all integers. The action of
$m\theta ^{i}$
are all integers. The action of
![]() $G(d)\cong G(1,d)/\mathbb {C}^{*}$
on
$G(d)\cong G(1,d)/\mathbb {C}^{*}$
on
![]() $R(1,d)$
induces a moment map:
$R(1,d)$
induces a moment map:
Define the Nakajima quiver variety
![]() $N(f,d)$
by the GIT quotient:
$N(f,d)$
by the GIT quotient:
There is also a description of Nakajima quiver varieties using the framed quiver in Subsection 2.3 given by Crawley–Boevey [Reference Crawley-Boevey3, Section 1].
2.6 Semiorthogonal decompositions
Let
![]() $\mathcal A$
be a triangulated category, and let
$\mathcal A$
be a triangulated category, and let
![]() $\mathcal A_{i}\subset \mathcal A$
be full triangulated subcategories for
$\mathcal A_{i}\subset \mathcal A$
be full triangulated subcategories for
![]() $1\leqslant i\leqslant n$
. We say that
$1\leqslant i\leqslant n$
. We say that
![]() $\mathcal A$
has a semiorthogonal decomposition
$\mathcal A$
has a semiorthogonal decomposition
if for every object
![]() $A_{i}\in \mathcal {A}_{i}$
and
$A_{i}\in \mathcal {A}_{i}$
and
![]() $A_{j}\in \mathcal {A}_{j}$
and
$A_{j}\in \mathcal {A}_{j}$
and
![]() $i<j$
we have
$i<j$
we have
![]() $\text {RHom}\,(A_{i},A_{j})=0$
, and the smallest full triangulated subcategory of
$\text {RHom}\,(A_{i},A_{j})=0$
, and the smallest full triangulated subcategory of
![]() $\mathcal {A}$
containing
$\mathcal {A}$
containing
![]() $\mathcal {A}_{i}$
for
$\mathcal {A}_{i}$
for
![]() $1\leqslant i\leqslant m$
is
$1\leqslant i\leqslant m$
is
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Let
![]() $\mathcal {B}$
be a triangulated subcategory of
$\mathcal {B}$
be a triangulated subcategory of
![]() $\mathcal {A}$
. There exists a semiorthogonal decomposition
$\mathcal {A}$
. There exists a semiorthogonal decomposition
![]() $\mathcal A=\langle \mathcal {C}, \mathcal {B}\rangle $
if and only if the inclusion
$\mathcal A=\langle \mathcal {C}, \mathcal {B}\rangle $
if and only if the inclusion
![]() $\mathcal {B}\hookrightarrow \mathcal A$
has a right adjoint
$\mathcal {B}\hookrightarrow \mathcal A$
has a right adjoint
![]() $\mathcal A\to \mathcal {B}$
. If this happens, we say that
$\mathcal A\to \mathcal {B}$
. If this happens, we say that
![]() $\mathcal {B}$
is right admissible in
$\mathcal {B}$
is right admissible in
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
2.7 Window categories
2.7.1
Let
![]() $\mathcal {X}=X/G$
be a quotient stack where G be a reductive group and X is a smooth affine variety with a G action.
$\mathcal {X}=X/G$
be a quotient stack where G be a reductive group and X is a smooth affine variety with a G action.
For pairs
![]() $(\lambda , Z)$
with
$(\lambda , Z)$
with
![]() $\lambda $
a cocharacter of G and Z a connected component of
$\lambda $
a cocharacter of G and Z a connected component of
![]() $X^{\lambda }$
, consider the diagram
$X^{\lambda }$
, consider the diagram
 $$ \begin{align} \mathcal{Z}:=Z/L\xleftarrow{q}\mathcal{S}:=S/P \xrightarrow{p} \mathcal{X}, \end{align} $$
$$ \begin{align} \mathcal{Z}:=Z/L\xleftarrow{q}\mathcal{S}:=S/P \xrightarrow{p} \mathcal{X}, \end{align} $$
where
![]() $S\subset X$
is the subset of points x such that
$S\subset X$
is the subset of points x such that
![]() $\lim _{z\to 0} \lambda (z)x\in Z$
, and L and P are the Levi and parabolic groups corresponding to
$\lim _{z\to 0} \lambda (z)x\in Z$
, and L and P are the Levi and parabolic groups corresponding to
![]() $\lambda $
. The map q is an affine bundle map, and the map p is proper. We say that
$\lambda $
. The map q is an affine bundle map, and the map p is proper. We say that
![]() $(\lambda , Z)$
is a Kempf–Ness stratum if the map p is a closed immersion. The map p is always a closed immersion if G is abelian.
$(\lambda , Z)$
is a Kempf–Ness stratum if the map p is a closed immersion. The map p is always a closed immersion if G is abelian.
2.7.2
Consider locally closed substacks
![]() $\mathcal {S}_{i}\subset \mathcal {X}$
indexed by
$\mathcal {S}_{i}\subset \mathcal {X}$
indexed by
![]() $i\in I$
for I a partially ordered set such that
$i\in I$
for I a partially ordered set such that
 $$ \begin{align*}\mathcal{S}_{i}\subset \mathcal{X}\setminus \bigcup_{j<i}\mathcal{S}_{j}\end{align*} $$
$$ \begin{align*}\mathcal{S}_{i}\subset \mathcal{X}\setminus \bigcup_{j<i}\mathcal{S}_{j}\end{align*} $$
is a Kempf–Ness stratum. We denote by
 $$ \begin{align*} \mathcal{U}&:=\bigcup_{i\in I}\mathcal{S}_{i},\\[3pt] \mathcal{X}^{\text{ss}}&:=\mathcal{X}\setminus\mathcal{U}. \end{align*} $$
$$ \begin{align*} \mathcal{U}&:=\bigcup_{i\in I}\mathcal{S}_{i},\\[3pt] \mathcal{X}^{\text{ss}}&:=\mathcal{X}\setminus\mathcal{U}. \end{align*} $$
It might happen that
![]() $\mathcal {X}^{\text {ss}}$
is empty. An example of such a stratification is given by the usual Kempf–Ness strata
$\mathcal {X}^{\text {ss}}$
is empty. An example of such a stratification is given by the usual Kempf–Ness strata
![]() $\mathcal {S}_{i}$
for
$\mathcal {S}_{i}$
for
![]() $i\in I$
and the semistable stack
$i\in I$
and the semistable stack
![]() $\mathcal {X}^{\text {ss}}\subset \mathcal {X}$
with respect to a linearization
$\mathcal {X}^{\text {ss}}\subset \mathcal {X}$
with respect to a linearization
![]() $\mathcal {L}$
on
$\mathcal {L}$
on
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
2.7.3
We continue with the notation from the previous subsection. Halpern–Leistner [Reference Halpern-Leistner11] constructed categories
![]() $\mathbb {G}_{w}\subset D^{b}(\mathcal {X})$
which are equivalent to
$\mathbb {G}_{w}\subset D^{b}(\mathcal {X})$
which are equivalent to
![]() $D^{b}\left (\mathcal {X}^{\text {ss}}\right )$
under the restriction map
$D^{b}\left (\mathcal {X}^{\text {ss}}\right )$
under the restriction map
![]() $j:\mathcal {X}^{\text {ss}}\hookrightarrow \mathcal {X}$
, which we now explain.
$j:\mathcal {X}^{\text {ss}}\hookrightarrow \mathcal {X}$
, which we now explain.
Let
![]() $i\in I$
. Assume that
$i\in I$
. Assume that
![]() $\mathcal {S}_{i}$
is an attracting locus for
$\mathcal {S}_{i}$
is an attracting locus for
![]() $(\lambda _{i}, Z_{i})$
. Consider the inclusion map
$(\lambda _{i}, Z_{i})$
. Consider the inclusion map
![]() $j_{i}:Z_{i}\hookrightarrow X$
. For
$j_{i}:Z_{i}\hookrightarrow X$
. For
![]() $w\in \mathbb {Z}$
, let
$w\in \mathbb {Z}$
, let
![]() $D^{b}(\mathcal {Z})_{w}$
be the subcategory of
$D^{b}(\mathcal {Z})_{w}$
be the subcategory of
![]() $D^{b}(\mathcal {Z})$
of complexes on which
$D^{b}(\mathcal {Z})$
of complexes on which
![]() $\lambda _{i}$
acts with weight w. Define
$\lambda _{i}$
acts with weight w. Define
 $n_{i}=\langle \lambda _{i}^{-1}, j_{i}^{*}\left (\det N_{p_{i}}\right )\rangle $
, where
$n_{i}=\langle \lambda _{i}^{-1}, j_{i}^{*}\left (\det N_{p_{i}}\right )\rangle $
, where
![]() $N_{p_{i}}$
is the normal bundle of
$N_{p_{i}}$
is the normal bundle of
![]() $\mathcal {S}_{i}$
in
$\mathcal {S}_{i}$
in
![]() $\mathcal {X}$
. Choose
$\mathcal {X}$
. Choose
![]() $w_{i}\in \mathbb {Z}$
, and define
$w_{i}\in \mathbb {Z}$
, and define
In [Reference Halpern-Leistner11, Theorem 2.10, Amplification 2.11], Halpern–Leistner constructs a semiorthogonal decomposition:
 $$ \begin{align} D^{b}(\mathcal{X})=\big\langle p_{i*}q_{i}^{*} D^{b}(\mathcal{Z}_{i})_{v_{i}},\mathbb{G}_{w}, p_{i*}q_{i}^{*} D^{b}(\mathcal{Z}_{i})_{t_{i}}\big\rangle, \end{align} $$
$$ \begin{align} D^{b}(\mathcal{X})=\big\langle p_{i*}q_{i}^{*} D^{b}(\mathcal{Z}_{i})_{v_{i}},\mathbb{G}_{w}, p_{i*}q_{i}^{*} D^{b}(\mathcal{Z}_{i})_{t_{i}}\big\rangle, \end{align} $$
where the categories on the left-hand side of
![]() $\mathbb {G}_{w}$
are after all
$\mathbb {G}_{w}$
are after all
![]() $i\in I$
and all
$i\in I$
and all
![]() $v_{i}<w_{i}$
, and the categories on the right-hand side of
$v_{i}<w_{i}$
, and the categories on the right-hand side of
![]() $\mathbb {G}_{w}$
are after all
$\mathbb {G}_{w}$
are after all
![]() $i\in I$
and all
$i\in I$
and all
![]() $t_{i}\geqslant w_{i}$
. The functors
$t_{i}\geqslant w_{i}$
. The functors
![]() $q_{i}^{*}$
and
$q_{i}^{*}$
and
![]() $p_{i*}$
are fully faithful on
$p_{i*}$
are fully faithful on
![]() $D^{b}(\mathcal {Z}_{i})_{v_{i}}$
and
$D^{b}(\mathcal {Z}_{i})_{v_{i}}$
and
![]() $q_{i}^{*}D^{b}(\mathcal {Z}_{i})_{v_{i}}$
, respectively, for
$q_{i}^{*}D^{b}(\mathcal {Z}_{i})_{v_{i}}$
, respectively, for
![]() $i\in I$
and
$i\in I$
and
![]() $v_{i}$
as above. The restriction functor
$v_{i}$
as above. The restriction functor
![]() $j^{*}:D^{b}(\mathcal {X})\to D^{b}\left (\mathcal {X}^{\text {ss}}\right )$
induces an equivalence of categories:
$j^{*}:D^{b}(\mathcal {X})\to D^{b}\left (\mathcal {X}^{\text {ss}}\right )$
induces an equivalence of categories:
2.8 Categories of singularities and matrix factorizations
A reference for this section is [Reference Toda35, Section 2.2]. Let Y be an affine scheme with an action of a reductive group G. Consider the quotient stack
![]() $\mathcal {Y}=Y/G$
. The category of singularities of
$\mathcal {Y}=Y/G$
. The category of singularities of
![]() $\mathcal {Y}$
is a triangulated category defined as the quotient of triangulated categories
$\mathcal {Y}$
is a triangulated category defined as the quotient of triangulated categories
 $$ \begin{align*}D_{\text{sg}}(\mathcal{Y}):=D^{b}(\mathcal{Y})/\text{Perf}(\mathcal{Y}),\end{align*} $$
$$ \begin{align*}D_{\text{sg}}(\mathcal{Y}):=D^{b}(\mathcal{Y})/\text{Perf}(\mathcal{Y}),\end{align*} $$
where
![]() $\text {Perf}(\mathcal {Y})\subset D^{b}(\mathcal {Y})$
is the full subcategory of perfect complexes. If
$\text {Perf}(\mathcal {Y})\subset D^{b}(\mathcal {Y})$
is the full subcategory of perfect complexes. If
![]() $\mathcal {Y}$
is smooth, the category of singularities is trivial. We have an exact sequence
$\mathcal {Y}$
is smooth, the category of singularities is trivial. We have an exact sequence
Let
![]() $\mathcal {X}=X/G$
be a smooth quotient stack with X an affine scheme, and consider a regular function
$\mathcal {X}=X/G$
be a smooth quotient stack with X an affine scheme, and consider a regular function
Consider the category of matrix factorizations
![]() $\text {MF}(\mathcal {X}, f)$
. It has objects
$\text {MF}(\mathcal {X}, f)$
. It has objects
![]() $(\mathbb {Z}/2\mathbb {Z})\times G$
-equivariant factorizations
$(\mathbb {Z}/2\mathbb {Z})\times G$
-equivariant factorizations
![]() $(P, d_{P})$
, where P is a G-equivariant coherent sheaf,
$(P, d_{P})$
, where P is a G-equivariant coherent sheaf,
![]() $\langle 1\rangle $
is the twist corresponding to a nontrivial
$\langle 1\rangle $
is the twist corresponding to a nontrivial
![]() $\mathbb {Z}/2\mathbb {Z}$
-character on X, and
$\mathbb {Z}/2\mathbb {Z}$
-character on X, and
with
![]() $d_{P}\circ d_{P}=f$
. Alternatively, the objects of
$d_{P}\circ d_{P}=f$
. Alternatively, the objects of
![]() $\text {MF}(\mathcal {X}, f)$
are tuplets
$\text {MF}(\mathcal {X}, f)$
are tuplets
where F and G are
![]() $ G$
-equivariant coherent sheaves,
$ G$
-equivariant coherent sheaves,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are G-equivariant morphisms with
$\beta $
are G-equivariant morphisms with
![]() $\alpha \circ \beta $
and
$\alpha \circ \beta $
and
![]() $\beta \circ \alpha $
are multiplication by f. By a theorem of Orlov [Reference Orlov22], there is an equivalence
$\beta \circ \alpha $
are multiplication by f. By a theorem of Orlov [Reference Orlov22], there is an equivalence
Recall that, for
![]() $f=0$
, the fiber
$f=0$
, the fiber
![]() $\mathcal {X}_{0}$
is derived. We will freely switch between
$\mathcal {X}_{0}$
is derived. We will freely switch between
![]() $D_{\text {sg}}$
and
$D_{\text {sg}}$
and
![]() $\text {MF}$
throughout this paper.
$\text {MF}$
throughout this paper.
For a triangulated subcategory
![]() $\mathcal {A}$
of
$\mathcal {A}$
of
![]() $D^{b}(\mathcal {X})$
, define
$D^{b}(\mathcal {X})$
, define
![]() $\text {MF}(\mathcal {A}, f)$
as the full subcategory of
$\text {MF}(\mathcal {A}, f)$
as the full subcategory of
![]() $\text {MF}(\mathcal {X}, f)$
with objects pairs
$\text {MF}(\mathcal {X}, f)$
with objects pairs
![]() $(P, d_{P})$
with P in
$(P, d_{P})$
with P in
![]() $\mathcal {A}$
. We explain next that semiorthogonal decompositions for the ambient smooth stack induce semiorthogonal decompositions for matrix factorizations; see also [Reference Halpern-Leistner and Pomerleano12, Lemma 1.18].
$\mathcal {A}$
. We explain next that semiorthogonal decompositions for the ambient smooth stack induce semiorthogonal decompositions for matrix factorizations; see also [Reference Halpern-Leistner and Pomerleano12, Lemma 1.18].
Proposition 2.1. Let I be a totally ordered set, and consider a semiorthogonal decomposition
 $$ \begin{align*}D^{b}(\mathcal{X})=\big\langle \mathcal{A}_{i}\big\rangle_{i\in I}.\end{align*} $$
$$ \begin{align*}D^{b}(\mathcal{X})=\big\langle \mathcal{A}_{i}\big\rangle_{i\in I}.\end{align*} $$
There is a semiorthogonal decomposition
 $$ \begin{align*}\text{MF}(\mathcal{X}, f)=\big\langle \text{MF}(\mathcal{A}_{i}, f)\big\rangle_{i\in I}.\end{align*} $$
$$ \begin{align*}\text{MF}(\mathcal{X}, f)=\big\langle \text{MF}(\mathcal{A}_{i}, f)\big\rangle_{i\in I}.\end{align*} $$
Proof. Assume for simplicity that the semiorthogonal decomposition is
 $$ \begin{align*}D^{b}(\mathcal{X})=\big\langle \mathcal{A}_{1}, \mathcal{A}_{2}\big\rangle.\end{align*} $$
$$ \begin{align*}D^{b}(\mathcal{X})=\big\langle \mathcal{A}_{1}, \mathcal{A}_{2}\big\rangle.\end{align*} $$
Consider an object
in
![]() $\text {MF}(\mathcal {X}, f)$
, and consider
$\text {MF}(\mathcal {X}, f)$
, and consider
![]() $F_{i}, G_{i}\in \mathcal {A}_{i}$
such that
$F_{i}, G_{i}\in \mathcal {A}_{i}$
such that
 $$ \begin{align*} F_{2}\to F&\to F_{1}\xrightarrow{[1]}\\ G_{2}\to G&\to G_{1}\xrightarrow{[1]}. \end{align*} $$
$$ \begin{align*} F_{2}\to F&\to F_{1}\xrightarrow{[1]}\\ G_{2}\to G&\to G_{1}\xrightarrow{[1]}. \end{align*} $$
The map
![]() $\alpha : F\to G$
induces a map
$\alpha : F\to G$
induces a map
![]() $\alpha : F_{2}\to G$
and thus a map
$\alpha : F_{2}\to G$
and thus a map
because
![]() $\text {RHom}(F_{2}, G_{1})=0$
. Further, it induces a map
$\text {RHom}(F_{2}, G_{1})=0$
. Further, it induces a map
![]() $\alpha : F\to G_{1}$
and thus a map
$\alpha : F\to G_{1}$
and thus a map
because
![]() $\text {RHom}(F_{2}, G_{1})=0$
. Similarly, there are induced maps
$\text {RHom}(F_{2}, G_{1})=0$
. Similarly, there are induced maps
![]() $\beta _{i}: G_{i}\to F_{i}$
for
$\beta _{i}: G_{i}\to F_{i}$
for
![]() $i=1,2$
. The tuplets
$i=1,2$
. The tuplets
are in
![]() $\text {MF}(\mathcal {A}_{i}, f)$
. There is a distinguished triangle
$\text {MF}(\mathcal {A}_{i}, f)$
. There is a distinguished triangle
 $$ \begin{align*}E_{1}\to E\to E_{2}\xrightarrow{[1]}.\end{align*} $$
$$ \begin{align*}E_{1}\to E\to E_{2}\xrightarrow{[1]}.\end{align*} $$
The orthogonality claim is immediate.
We say that f satisfies Assumption A if there is an extra action of
![]() $\mathbb {C}^{*}$
on X which commutes with the action of G such that f is
$\mathbb {C}^{*}$
on X which commutes with the action of G such that f is
![]() $\mathbb {C}^{*}$
-equivariant of weight
$\mathbb {C}^{*}$
-equivariant of weight
![]() $2$
. Denote by
$2$
. Denote by
![]() $(1)$
the twist by the character
$(1)$
the twist by the character
Consider the category of graded matrix factorizations
![]() $\text {MF}^{\text {gr}}(\mathcal {X}, f)$
. It has objects pairs
$\text {MF}^{\text {gr}}(\mathcal {X}, f)$
. It has objects pairs
![]() $(P, d_{P})$
with P an equivariant
$(P, d_{P})$
with P an equivariant
![]() $G\times \mathbb {C}^{*}$
-sheaf on X and
$G\times \mathbb {C}^{*}$
-sheaf on X and
![]() $d_{P}:P\to P(1)$
a
$d_{P}:P\to P(1)$
a
![]() $G\times \mathbb {C}^{*}$
-equivariant morphism. For f zero and the trivial
$G\times \mathbb {C}^{*}$
-equivariant morphism. For f zero and the trivial
![]() $\mathbb {C}^{*}$
-action on
$\mathbb {C}^{*}$
-action on
![]() $\mathcal {X}$
, we have that
$\mathcal {X}$
, we have that
(see [Reference Toda35, Remark 2.3.7]). For a triangulated subcategory
![]() $\mathcal {B}$
of
$\mathcal {B}$
of
![]() $D^{b}_{\mathbb {C}^{*}}(\mathcal {X})$
, define
$D^{b}_{\mathbb {C}^{*}}(\mathcal {X})$
, define
![]() $\text {MF}^{\text {gr}}(\mathcal {B}, f)$
as the full subcategory of
$\text {MF}^{\text {gr}}(\mathcal {B}, f)$
as the full subcategory of
![]() $\text {MF}^{\text {gr}}(\mathcal {X}, f)$
with objects pairs
$\text {MF}^{\text {gr}}(\mathcal {X}, f)$
with objects pairs
![]() $(P, d_{P})$
with P in
$(P, d_{P})$
with P in
![]() $\mathcal {B}$
. The same argument used in Proposition 2.1 shows that:
$\mathcal {B}$
. The same argument used in Proposition 2.1 shows that:
Proposition 2.2. Let I be a totally ordered set and consider a semiorthogonal decomposition
 $$ \begin{align*}D^{b}_{\mathbb{C}^{*}}(\mathcal{X})=\big\langle \mathcal{B}_{i}\big\rangle_{i\in I}.\end{align*} $$
$$ \begin{align*}D^{b}_{\mathbb{C}^{*}}(\mathcal{X})=\big\langle \mathcal{B}_{i}\big\rangle_{i\in I}.\end{align*} $$
There is a semiorthogonal decomposition
 $$ \begin{align*}\text{MF}^{\text{gr}}(\mathcal{X}, f)=\big\langle \text{MF}^{\text{gr}}(\mathcal{B}_{i}, f)\big\rangle_{i\in I}.\end{align*} $$
$$ \begin{align*}\text{MF}^{\text{gr}}(\mathcal{X}, f)=\big\langle \text{MF}^{\text{gr}}(\mathcal{B}_{i}, f)\big\rangle_{i\in I}.\end{align*} $$
2.9 Functoriality of categories of singularities
References for this subsection are [Reference Polishchuk and Vaintrob26], [Reference Toda35]. Let
![]() $\mathcal {X}$
,
$\mathcal {X}$
,
![]() $\mathcal {X}^{\prime }$
be smooth quotient stacks (see (4)) with a map
$\mathcal {X}^{\prime }$
be smooth quotient stacks (see (4)) with a map
![]() $\alpha : \mathcal {X}^{\prime }\to \mathcal {X}$
. Let
$\alpha : \mathcal {X}^{\prime }\to \mathcal {X}$
. Let
be a regular function, and consider
![]() $f^{\prime }:=f\alpha :\mathcal {X}^{\prime }\to \mathbb {A}^{1}_{\mathbb {C}}.$
Assume that
$f^{\prime }:=f\alpha :\mathcal {X}^{\prime }\to \mathbb {A}^{1}_{\mathbb {C}}.$
Assume that
![]() $0$
is the only critical value for each of f and
$0$
is the only critical value for each of f and
![]() $f^{\prime }$
. There is a functor
$f^{\prime }$
. There is a functor
 $$ \begin{align*} \alpha^{*}: \text{MF}(\mathcal{X}, f)&\to \text{MF}\left(\mathcal{X}^{\prime}, f^{\prime}\right),\\[3pt] (P, d_{P})&\mapsto\left(\alpha^{*}P, \alpha^{*}d_{P}\right). \end{align*} $$
$$ \begin{align*} \alpha^{*}: \text{MF}(\mathcal{X}, f)&\to \text{MF}\left(\mathcal{X}^{\prime}, f^{\prime}\right),\\[3pt] (P, d_{P})&\mapsto\left(\alpha^{*}P, \alpha^{*}d_{P}\right). \end{align*} $$
If
![]() $\alpha $
is proper, there is a functor
$\alpha $
is proper, there is a functor
 $$ \begin{align*} \alpha_{*}: \text{MF}\left(\mathcal{X}^{\prime}, f^{\prime}\right)&\to \text{MF}(\mathcal{X}, f),\\[3pt] \left(P^{\prime}, d_{P^{\prime}}\right)&\mapsto\left(\alpha_{*}P^{\prime}, \alpha_{*}d_{P^{\prime}}\right). \end{align*} $$
$$ \begin{align*} \alpha_{*}: \text{MF}\left(\mathcal{X}^{\prime}, f^{\prime}\right)&\to \text{MF}(\mathcal{X}, f),\\[3pt] \left(P^{\prime}, d_{P^{\prime}}\right)&\mapsto\left(\alpha_{*}P^{\prime}, \alpha_{*}d_{P^{\prime}}\right). \end{align*} $$
Assume there are
![]() $\mathbb {C}^{*}$
-actions on
$\mathbb {C}^{*}$
-actions on
![]() $\mathcal {X}^{\prime }$
and
$\mathcal {X}^{\prime }$
and
![]() $\mathcal {X}$
such that
$\mathcal {X}$
such that
![]() $\alpha $
is
$\alpha $
is
![]() $\mathbb {C}^{*}$
-equivariant and such that
$\mathbb {C}^{*}$
-equivariant and such that
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {X}^{\prime }$
satisfy Assumption A with respect to the
$\mathcal {X}^{\prime }$
satisfy Assumption A with respect to the
![]() $\mathbb {C}^{*}$
-action. There are pullback and pushforward functors
$\mathbb {C}^{*}$
-action. There are pullback and pushforward functors
 $$ \begin{align*} \alpha^{*}&: \text{MF}^{\text{gr}}(\mathcal{X}, f)\to \text{MF}^{\text{gr}}\left(\mathcal{X}^{\prime}, f^{\prime}\right),\\[3pt] \alpha_{*}&: \text{MF}^{\text{gr}}\left(\mathcal{X}^{\prime}, f^{\prime}\right)\to \text{MF}^{\text{gr}}(\mathcal{X}, f). \end{align*} $$
$$ \begin{align*} \alpha^{*}&: \text{MF}^{\text{gr}}(\mathcal{X}, f)\to \text{MF}^{\text{gr}}\left(\mathcal{X}^{\prime}, f^{\prime}\right),\\[3pt] \alpha_{*}&: \text{MF}^{\text{gr}}\left(\mathcal{X}^{\prime}, f^{\prime}\right)\to \text{MF}^{\text{gr}}(\mathcal{X}, f). \end{align*} $$
There are also such functors for categories of singularities. These pullback and pushforward functors satisfy properties as those for derived categories, for example proper base change for Cartesian diagrams.
2.10 Thom–Sebastiani theorem
Let
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}$
be smooth quotient stacks with regular functions
$\mathcal {Y}$
be smooth quotient stacks with regular functions
 $$ \begin{align*} f&:\mathcal{X}\to\mathbb{A}^{1}_{\mathbb{C}},\\[3pt] g&:\mathcal{Y}\to\mathbb{A}^{1}_{\mathbb{C}},\\[3pt] f+g&:\mathcal{X}\times\mathcal{Y}\to\mathbb{A}^{1}_{\mathbb{C}}. \end{align*} $$
$$ \begin{align*} f&:\mathcal{X}\to\mathbb{A}^{1}_{\mathbb{C}},\\[3pt] g&:\mathcal{Y}\to\mathbb{A}^{1}_{\mathbb{C}},\\[3pt] f+g&:\mathcal{X}\times\mathcal{Y}\to\mathbb{A}^{1}_{\mathbb{C}}. \end{align*} $$
Consider the functors induced by exterior tensor product (see [Reference Ballard, Favero and Katzarkov1, Definition 3.22]):
 $$ \begin{align*} \text{TS}&:\text{MF}^{\text{gr}}(\mathcal{X}, f)\otimes \text{MF}^{\text{gr}}(\mathcal{Y}, g)\to \text{MF}^{\text{gr}}(\mathcal{X}\times\mathcal{Y}, f+g),\\[3pt] \text{TS}&:\text{MF}(\mathcal{X}, f)\otimes \text{MF}(\mathcal{Y}, g)\to \text{MF}(\mathcal{X}\times\mathcal{Y}, f+g). \end{align*} $$
$$ \begin{align*} \text{TS}&:\text{MF}^{\text{gr}}(\mathcal{X}, f)\otimes \text{MF}^{\text{gr}}(\mathcal{Y}, g)\to \text{MF}^{\text{gr}}(\mathcal{X}\times\mathcal{Y}, f+g),\\[3pt] \text{TS}&:\text{MF}(\mathcal{X}, f)\otimes \text{MF}(\mathcal{Y}, g)\to \text{MF}(\mathcal{X}\times\mathcal{Y}, f+g). \end{align*} $$
To define the first functor above, we assume that
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}$
satisfy Assumption A and denote the corresponding tori by
$\mathcal {Y}$
satisfy Assumption A and denote the corresponding tori by
![]() $\mathbb {C}^{*}_{1}$
and
$\mathbb {C}^{*}_{1}$
and
![]() $\mathbb {C}^{*}_{2}$
; the corresponding
$\mathbb {C}^{*}_{2}$
; the corresponding
![]() $\mathbb {C}^{*}$
on
$\mathbb {C}^{*}$
on
![]() $\mathcal {X}\times \mathcal {Y}$
is the diagonal
$\mathcal {X}\times \mathcal {Y}$
is the diagonal
![]() $\mathbb {C}^{*}\hookrightarrow \mathbb {C}^{*}_{1}\times \mathbb {C}^{*}_{2}$
.
$\mathbb {C}^{*}\hookrightarrow \mathbb {C}^{*}_{1}\times \mathbb {C}^{*}_{2}$
.
The Thom–Sebastiani theorem says that the first functor is an equivalence [Reference Ballard, Favero and Katzarkov1, Section 3 and Section 5.1], [Reference Efimov and Positselski10, Section 2.5]:
There is also a version when a version of the second one is an equivalence [Reference Preygel27]. When using categories of singularities, the Thom–Sebastiani functor is induced by pushforward along
![]() $i:\mathcal {X}_{0}\times \mathcal {Y}_{0}\hookrightarrow (\mathcal {X}\times \mathcal {Y})_{0}$
(see [Reference Preygel27, Theorem 4.13]):
$i:\mathcal {X}_{0}\times \mathcal {Y}_{0}\hookrightarrow (\mathcal {X}\times \mathcal {Y})_{0}$
(see [Reference Preygel27, Theorem 4.13]):
There are maps
 $$ \begin{align*} \text{TS}&:K_{0}\left(\text{MF}^{\text{gr}}(\mathcal{X}, f)\right)\otimes K_{0}\left(\text{MF}^{\text{gr}}(\mathcal{Y}, g)\right)\to K_{0}\left(\text{MF}^{\text{gr}}(\mathcal{X}\times\mathcal{Y}, f+g)\right),\\[3pt] \text{TS}&:K_{0}\left(\text{MF}(\mathcal{X}, f)\right)\otimes K_{0}\left(\text{MF}(\mathcal{Y}, g)\right)\to K_{0}\left(\text{MF}(\mathcal{X}\times\mathcal{Y}, f+g)\right). \end{align*} $$
$$ \begin{align*} \text{TS}&:K_{0}\left(\text{MF}^{\text{gr}}(\mathcal{X}, f)\right)\otimes K_{0}\left(\text{MF}^{\text{gr}}(\mathcal{Y}, g)\right)\to K_{0}\left(\text{MF}^{\text{gr}}(\mathcal{X}\times\mathcal{Y}, f+g)\right),\\[3pt] \text{TS}&:K_{0}\left(\text{MF}(\mathcal{X}, f)\right)\otimes K_{0}\left(\text{MF}(\mathcal{Y}, g)\right)\to K_{0}\left(\text{MF}(\mathcal{X}\times\mathcal{Y}, f+g)\right). \end{align*} $$
In general, these maps are not isomorphisms.
2.11 Dimensional reduction
Let X be a smooth affine scheme with an action of a reductive group G, let
![]() $\mathcal {X}=X/G$
and let E be a G-equivariant vector bundle on X. Let
$\mathcal {X}=X/G$
and let E be a G-equivariant vector bundle on X. Let
![]() $\mathbb {C}^{*}$
act on the fibers of E with weight
$\mathbb {C}^{*}$
act on the fibers of E with weight
![]() $2$
, and consider
$2$
, and consider
![]() $s\in \Gamma (X, E)$
a section of E of
$s\in \Gamma (X, E)$
a section of E of
![]() $\mathbb {C}^{*}$
-weight
$\mathbb {C}^{*}$
-weight
![]() $2$
. It induces a map
$2$
. It induces a map
![]() $\partial : E^{\vee }\to \mathcal {O}_{X}$
. Consider the Köszul stack
$\partial : E^{\vee }\to \mathcal {O}_{X}$
. Consider the Köszul stack
 $$ \begin{align*}\mathfrak{P}:=\text{Spec}\left(\mathcal{O}_{X}\left[E^{\vee}[1];\partial\right]\right)\big/G.\end{align*} $$
$$ \begin{align*}\mathfrak{P}:=\text{Spec}\left(\mathcal{O}_{X}\left[E^{\vee}[1];\partial\right]\right)\big/G.\end{align*} $$
The section s also induces the regular function
defined by
![]() $w(x,v)=\langle s(x), v \rangle $
for
$w(x,v)=\langle s(x), v \rangle $
for
![]() $x\in X(\mathbb {C})$
and
$x\in X(\mathbb {C})$
and
![]() $v\in E^{\vee }|_{x}$
. Consider the category of graded matrix factorizations
$v\in E^{\vee }|_{x}$
. Consider the category of graded matrix factorizations
![]() $\text {MF}^{\text {gr}}\left (\mathcal {E}, w\right )$
with respect to the group
$\text {MF}^{\text {gr}}\left (\mathcal {E}, w\right )$
with respect to the group
![]() $\mathbb {C}^{*}$
mentioned above. There is an equivalence of categories due to Isik [Reference Isik13], called dimensional reduction or the Köszul equivalence:
$\mathbb {C}^{*}$
mentioned above. There is an equivalence of categories due to Isik [Reference Isik13], called dimensional reduction or the Köszul equivalence:
The analogous result in cohomology was proved by Davison [Reference Davison4].
2.12 Localization theorems for categories of singularities
We discuss some properties of categories of singularities on stacks which are used for computations in KHAs.
Proposition 2.3. Let X be an affine scheme with an action of a reductive group G, and consider the stack
![]() $\mathcal {X}=X/G$
. Let
$\mathcal {X}=X/G$
. Let
![]() $B\subset G$
be a Borel subgroup with maximal torus T, and let
$B\subset G$
be a Borel subgroup with maximal torus T, and let
![]() $\mathcal {Y}:=X/B$
and
$\mathcal {Y}:=X/B$
and
![]() $\mathcal {Z}=X/T$
. There are natural maps
$\mathcal {Z}=X/T$
. There are natural maps
![]() $\tau :\mathcal {Z}\to \mathcal {Y}$
and
$\tau :\mathcal {Z}\to \mathcal {Y}$
and
![]() $\pi :\mathcal {Y}\to \mathcal {X}$
. Then
$\pi :\mathcal {Y}\to \mathcal {X}$
. Then
 $$ \begin{align*} \pi^{*}&: G_{0}(\mathcal{X})\hookrightarrow G_{0}(\mathcal{Y}),\\[3pt] \pi^{*}&: K_{0}(\mathcal{X})\hookrightarrow K_{0}(\mathcal{Y}),\\[3pt] \tau^{*}&: G_{0}(\mathcal{Y})\cong G_{0}(\mathcal{Z}),\\[3pt] \tau^{*}&: K_{0}(\mathcal{Y})\cong K_{0}(\mathcal{Z}). \end{align*} $$
$$ \begin{align*} \pi^{*}&: G_{0}(\mathcal{X})\hookrightarrow G_{0}(\mathcal{Y}),\\[3pt] \pi^{*}&: K_{0}(\mathcal{X})\hookrightarrow K_{0}(\mathcal{Y}),\\[3pt] \tau^{*}&: G_{0}(\mathcal{Y})\cong G_{0}(\mathcal{Z}),\\[3pt] \tau^{*}&: K_{0}(\mathcal{Y})\cong K_{0}(\mathcal{Z}). \end{align*} $$
Proof. The map
![]() $\tau $
is an affine bundle map, so
$\tau $
is an affine bundle map, so
![]() $\tau ^{*}$
is an isomorphism in K and G-theory.
$\tau ^{*}$
is an isomorphism in K and G-theory.
Next, we have that
![]() $\mathcal {Y}=\left (X\times _{B} G\right )/G$
. The map
$\mathcal {Y}=\left (X\times _{B} G\right )/G$
. The map
![]() $\pi ^{*}$
is fully faithful by the projection formula and
$\pi ^{*}$
is fully faithful by the projection formula and
![]() $\pi _{*}\mathcal {O}_{\mathcal {Y}}=\mathcal {O}_{\mathcal {X}}$
. It has a right adjoint
$\pi _{*}\mathcal {O}_{\mathcal {Y}}=\mathcal {O}_{\mathcal {X}}$
. It has a right adjoint
![]() $\pi _{*}$
. Thus, the categories
$\pi _{*}$
. Thus, the categories
 $$ \begin{align*} \pi^{*}&: D^{b}(\mathcal{X})\to D^{b}(\mathcal{Y})\\[3pt] \pi^{*}&: \text{Perf}(\mathcal{X})\to \text{Perf}(\mathcal{Y}) \end{align*} $$
$$ \begin{align*} \pi^{*}&: D^{b}(\mathcal{X})\to D^{b}(\mathcal{Y})\\[3pt] \pi^{*}&: \text{Perf}(\mathcal{X})\to \text{Perf}(\mathcal{Y}) \end{align*} $$
are admissible, and the conclusion follows.
Assume next that
![]() $\mathcal {X}=X/T$
for a vector space X with an action of a torus T. Consider a regular function
$\mathcal {X}=X/T$
for a vector space X with an action of a torus T. Consider a regular function
with
![]() $0$
the only critical value. Let
$0$
the only critical value. Let
![]() $\lambda :\mathbb {C}^{*}\to T$
be a cocharacter, and let
$\lambda :\mathbb {C}^{*}\to T$
be a cocharacter, and let
![]() $w\in \mathbb {Z}$
. Define
$w\in \mathbb {Z}$
. Define
 $$ \begin{align*}D^{b}(BT)_{\geqslant w}\subset D^{b}(BT)\end{align*} $$
$$ \begin{align*}D^{b}(BT)_{\geqslant w}\subset D^{b}(BT)\end{align*} $$
the subcategory of complexes on which
![]() $\lambda $
acts with weights
$\lambda $
acts with weights
![]() $\geqslant w$
. It induces a filtration
$\geqslant w$
. It induces a filtration
![]() $K_{0}(BT)_{\geqslant w}\subset K_{0}(BT)$
. We denote its associated graded pieces by
$K_{0}(BT)_{\geqslant w}\subset K_{0}(BT)$
. We denote its associated graded pieces by
![]() $\text {gr}_{w} K_{0}(BT)$
. Let
$\text {gr}_{w} K_{0}(BT)$
. Let
![]() $a: X^{\lambda }/T\hookrightarrow \mathcal {X}$
. It induces a functor
$a: X^{\lambda }/T\hookrightarrow \mathcal {X}$
. It induces a functor
 $a^{*}: D_{\text {sg}}(\mathcal {X}_{0})\to D_{\text {sg}}\left (X^{\lambda }_{0}/T\right )$
. Let
$a^{*}: D_{\text {sg}}(\mathcal {X}_{0})\to D_{\text {sg}}\left (X^{\lambda }_{0}/T\right )$
. Let
be the subcategory of complexes
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\lambda $
acts with weights
$\lambda $
acts with weights
![]() $\geqslant w$
on
$\geqslant w$
on
![]() $a^{*}(F)$
. It induces a filtration
$a^{*}(F)$
. It induces a filtration
 $$ \begin{align*}K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right)_{\geqslant w}\subset K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right).\end{align*} $$
$$ \begin{align*}K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right)_{\geqslant w}\subset K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right).\end{align*} $$
We denote its associated graded pieces by
![]() $\text {gr}_{w} K_{0}\left (D_{\text {sg}}(\mathcal {X}_{0})\right )$
.
$\text {gr}_{w} K_{0}\left (D_{\text {sg}}(\mathcal {X}_{0})\right )$
.
![]() $K_{0}(BT)$
acts on
$K_{0}(BT)$
acts on
![]() $K_{0}\left (D_{\text {sg}}(\mathcal {X}_{0})\right )$
via the tensor product and respects the above filtrations.
$K_{0}\left (D_{\text {sg}}(\mathcal {X}_{0})\right )$
via the tensor product and respects the above filtrations.
Next, assume that
![]() $\mathcal {E}$
is a vector bundle on
$\mathcal {E}$
is a vector bundle on
![]() $\mathcal {X}$
, and consider the zero section
$\mathcal {X}$
, and consider the zero section
![]() $\iota :\mathcal {X}\hookrightarrow \mathcal {E}$
. Define the Euler class
$\iota :\mathcal {X}\hookrightarrow \mathcal {E}$
. Define the Euler class
![]() $\text {eu}(\mathcal {E}):=\iota ^{*}\iota _{*}(1)\in K_{0}(BT)\cong K_{0}(\mathcal {X}).$
$\text {eu}(\mathcal {E}):=\iota ^{*}\iota _{*}(1)\in K_{0}(BT)\cong K_{0}(\mathcal {X}).$
Proposition 2.4. We are continuing in the above framework. Assume that there exists
![]() $\lambda :\mathbb {C}^{*}\hookrightarrow T$
such that
$\lambda :\mathbb {C}^{*}\hookrightarrow T$
such that
![]() $\mathcal {E}^{\lambda }=\mathcal {X}$
. Then the class
$\mathcal {E}^{\lambda }=\mathcal {X}$
. Then the class
![]() $\text {eu}\,(\mathcal {E})$
is not a zero divisor in
$\text {eu}\,(\mathcal {E})$
is not a zero divisor in
![]() $K_{0}\left (D_{\text {sg}}(\mathcal {X}_{0})\right ).$
$K_{0}\left (D_{\text {sg}}(\mathcal {X}_{0})\right ).$
Proof. Let S be the set of weights of the normal bundle
![]() $N_{\iota }$
. We have that
$N_{\iota }$
. We have that
 $$ \begin{align*}\text{eu}(\mathcal{E})=\prod_{\beta\in S}(1-q^{\beta})\in K_{0}(B\mathbb{C}^{*}).\end{align*} $$
$$ \begin{align*}\text{eu}(\mathcal{E})=\prod_{\beta\in S}(1-q^{\beta})\in K_{0}(B\mathbb{C}^{*}).\end{align*} $$
The hypothesis implies that
![]() $\langle \lambda , \beta \rangle $
is not zero for
$\langle \lambda , \beta \rangle $
is not zero for
![]() $\beta \in S$
. Let v be the smallest
$\beta \in S$
. Let v be the smallest
![]() $\lambda $
-weight of a monomial in
$\lambda $
-weight of a monomial in
![]() $\text {eu}(\mathcal {E})$
. Then
$\text {eu}(\mathcal {E})$
. Then
Let
![]() $w\in \mathbb {Z}$
. Multiplication by
$w\in \mathbb {Z}$
. Multiplication by
![]() $\text {eu}(\mathcal {E})$
induces the multiplication by
$\text {eu}(\mathcal {E})$
induces the multiplication by
![]() $\pm q^{v}$
-map
$\pm q^{v}$
-map
 $$ \begin{align*}\text{gr}_{w} K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right)\xrightarrow{\sim} \text{gr}_{v+w} K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right),\end{align*} $$
$$ \begin{align*}\text{gr}_{w} K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right)\xrightarrow{\sim} \text{gr}_{v+w} K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right),\end{align*} $$
so
![]() $\text {eu}(\mathcal {E})$
is not a zero divisor.
$\text {eu}(\mathcal {E})$
is not a zero divisor.
For the next result, let T be a torus, let X be a representation of T, and let
![]() $Y\hookrightarrow X$
a T-equivariant affine subscheme. Denote by S the set of weights
$Y\hookrightarrow X$
a T-equivariant affine subscheme. Denote by S the set of weights
![]() $\beta $
of T in
$\beta $
of T in
![]() $X/X^{T}$
and by
$X/X^{T}$
and by
![]() $\mathcal {I}$
the set of functions
$\mathcal {I}$
the set of functions
![]() $1-q^{\beta }$
with
$1-q^{\beta }$
with
![]() $\beta \in S$
. Consider the stack
$\beta \in S$
. Consider the stack
![]() $\mathcal {X}=X/T$
. For M a
$\mathcal {X}=X/T$
. For M a
![]() $K_{0}(BT)$
-module, we denote by
$K_{0}(BT)$
-module, we denote by
![]() $M_{\mathcal {I}}$
the localization of M at functions in
$M_{\mathcal {I}}$
the localization of M at functions in
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Theorem 2.5. Let
![]() $f:\mathcal {X}\to \mathbb {A}^{1}_{\mathbb {C}}$
be a regular function, and let
$f:\mathcal {X}\to \mathbb {A}^{1}_{\mathbb {C}}$
be a regular function, and let
![]() $\lambda :\mathbb {C}^{*}\to T$
be a cocharacter. Consider the attracting diagram for
$\lambda :\mathbb {C}^{*}\to T$
be a cocharacter. Consider the attracting diagram for
![]() $\lambda $
:
$\lambda $
:
 $$ \begin{align*}\mathcal{Z}:=X^{\lambda}/T\xleftarrow{q}\mathcal{S}:=X^{\lambda\geqslant 0}/T \xrightarrow{p} \mathcal{X}.\end{align*} $$
$$ \begin{align*}\mathcal{Z}:=X^{\lambda}/T\xleftarrow{q}\mathcal{S}:=X^{\lambda\geqslant 0}/T \xrightarrow{p} \mathcal{X}.\end{align*} $$
Let
![]() $\iota :\mathcal {Z}\hookrightarrow \mathcal {X}$
be the natural inclusion map. There are isomorphisms
$\iota :\mathcal {Z}\hookrightarrow \mathcal {X}$
be the natural inclusion map. There are isomorphisms
 $$ \begin{align*} p_{*}q^{*}&: K_{0}\left(D_{\text{sg}}(\mathcal{Z}_{0})\right)_{\mathcal{I}}\xrightarrow{\sim} K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right)_{\mathcal{I}},\\[3pt] \iota_{*}&: K_{0}\left(D_{\text{sg}}(\mathcal{Z}_{0})\right)_{\mathcal{I}}\xrightarrow{\sim} K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right)_{\mathcal{I}},\\[3pt] \iota^{*}&:K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right)_{\mathcal{I}}\xrightarrow{\sim} K_{0}\left(D_{\text{sg}}(\mathcal{Z}_{0})\right)_{\mathcal{I}}. \end{align*} $$
$$ \begin{align*} p_{*}q^{*}&: K_{0}\left(D_{\text{sg}}(\mathcal{Z}_{0})\right)_{\mathcal{I}}\xrightarrow{\sim} K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right)_{\mathcal{I}},\\[3pt] \iota_{*}&: K_{0}\left(D_{\text{sg}}(\mathcal{Z}_{0})\right)_{\mathcal{I}}\xrightarrow{\sim} K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right)_{\mathcal{I}},\\[3pt] \iota^{*}&:K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right)_{\mathcal{I}}\xrightarrow{\sim} K_{0}\left(D_{\text{sg}}(\mathcal{Z}_{0})\right)_{\mathcal{I}}. \end{align*} $$
We review Takeda’s localization theorem in K-theory [Reference Takeda33].
Proposition 2.6. In the above framework, we have that
![]() $G_{i}^{T}(Y\setminus Y^{T})_{\mathcal {I}}=0$
for any
$G_{i}^{T}(Y\setminus Y^{T})_{\mathcal {I}}=0$
for any
![]() $i\geqslant 0$
.
$i\geqslant 0$
.
Proof. This follows from Takeda’s original argument [Reference Takeda33, page 79]. Let
![]() $\iota :X^{T}\hookrightarrow X$
be the natural inclusion.
$\iota :X^{T}\hookrightarrow X$
be the natural inclusion.
![]() $G_{i}^{T}(Y\setminus Y^{T})$
is a
$G_{i}^{T}(Y\setminus Y^{T})$
is a
![]() $K_{0}^{T}(Y\setminus Y^{T})$
-module, so it suffices to show that
$K_{0}^{T}(Y\setminus Y^{T})$
-module, so it suffices to show that
![]() $K_{0}^{T}(Y\setminus Y^{T})_{\mathcal {I}}=0$
. There is a restriction map of rings
$K_{0}^{T}(Y\setminus Y^{T})_{\mathcal {I}}=0$
. There is a restriction map of rings
 $$ \begin{align*}K_{0}^{T}\left(X\setminus X^{T}\right)\to K_{0}^{T}\left(Y\setminus Y^{T}\right).\end{align*} $$
$$ \begin{align*}K_{0}^{T}\left(X\setminus X^{T}\right)\to K_{0}^{T}\left(Y\setminus Y^{T}\right).\end{align*} $$
It suffices to show that
![]() $K_{0}^{T}(X\setminus X^{T})_{\mathcal {I}}=0$
because then the unit of
$K_{0}^{T}(X\setminus X^{T})_{\mathcal {I}}=0$
because then the unit of
![]() $K_{0}^{T}(Y\setminus Y^{T})_{\mathcal {I}}$
is annihilated, and so
$K_{0}^{T}(Y\setminus Y^{T})_{\mathcal {I}}$
is annihilated, and so
![]() $K_{0}^{T}(Y\setminus Y^{T})_{\mathcal {I}}=0$
. It thus suffices to show that
$K_{0}^{T}(Y\setminus Y^{T})_{\mathcal {I}}=0$
. It thus suffices to show that
 $$ \begin{align*}\iota_{*}: K_{0}^{T}\left(X^{T}\right)_{\mathcal{I}} \xrightarrow{\sim} K_{0}^{T}\left(X\right)_{\mathcal{I}}.\end{align*} $$
$$ \begin{align*}\iota_{*}: K_{0}^{T}\left(X^{T}\right)_{\mathcal{I}} \xrightarrow{\sim} K_{0}^{T}\left(X\right)_{\mathcal{I}}.\end{align*} $$
This is true because
![]() $\iota _{*}$
is multiplication by
$\iota _{*}$
is multiplication by
 $\prod _{\beta \in S}\left (1-q^{\beta }\right )$
.
$\prod _{\beta \in S}\left (1-q^{\beta }\right )$
.
Proof of Theorem 2.5
Let
![]() $\mathcal {U}:=\mathcal {X}\setminus \mathcal {S}\subset \mathcal {X}$
. Consider the natural inclusion
$\mathcal {U}:=\mathcal {X}\setminus \mathcal {S}\subset \mathcal {X}$
. Consider the natural inclusion
![]() $t:\mathcal {Z}\hookrightarrow \mathcal {S}$
. Then
$t:\mathcal {Z}\hookrightarrow \mathcal {S}$
. Then
![]() $\iota =p\circ t$
. By Proposition 2.1 and the semiorthogonal decomposition (6), there are semiorthogonal decompositions:
$\iota =p\circ t$
. By Proposition 2.1 and the semiorthogonal decomposition (6), there are semiorthogonal decompositions:
 $$ \begin{align*} D_{\text{sg}}(\mathcal{X}_{0})&=\big\langle D_{\text{sg}}(\mathcal{Z}_{0})_{<w}, \mathbb{D}_{w}, D_{\text{sg}}(\mathcal{Z}_{0})_{\geqslant w}\big\rangle,\\[3pt] D_{\text{sg}}(\mathcal{Z}_{0})&=\big\langle D_{\text{sg}}(\mathcal{Z}_{0})_{<w}, D_{\text{sg}}(\mathcal{Z}_{0})_{\geqslant w}\big\rangle \end{align*} $$
$$ \begin{align*} D_{\text{sg}}(\mathcal{X}_{0})&=\big\langle D_{\text{sg}}(\mathcal{Z}_{0})_{<w}, \mathbb{D}_{w}, D_{\text{sg}}(\mathcal{Z}_{0})_{\geqslant w}\big\rangle,\\[3pt] D_{\text{sg}}(\mathcal{Z}_{0})&=\big\langle D_{\text{sg}}(\mathcal{Z}_{0})_{<w}, D_{\text{sg}}(\mathcal{Z}_{0})_{\geqslant w}\big\rangle \end{align*} $$
with
![]() $\mathbb {D}_{w}\cong D_{\text {sg}}(\mathcal {U}_{0})$
by (6). By passing to the Grothendieck group, there is a decomposition
$\mathbb {D}_{w}\cong D_{\text {sg}}(\mathcal {U}_{0})$
by (6). By passing to the Grothendieck group, there is a decomposition
where the map
![]() $K_{0}\left (D_{\text {sg}}(\mathcal {Z}_{0})\right )\to K_{0}\left (D_{\text {sg}}(\mathcal {X}_{0})\right )$
is
$K_{0}\left (D_{\text {sg}}(\mathcal {Z}_{0})\right )\to K_{0}\left (D_{\text {sg}}(\mathcal {X}_{0})\right )$
is
![]() $p_{*}q^{*}$
. We show that
$p_{*}q^{*}$
. We show that
By the definition of the category of singularities, the map
![]() $G_{0}(\mathcal {U}_{0})\twoheadrightarrow K_{0}\left (D_{\text {sg}}(\mathcal {U}_{0})\right )$
is surjective. We have that
$G_{0}(\mathcal {U}_{0})\twoheadrightarrow K_{0}\left (D_{\text {sg}}(\mathcal {U}_{0})\right )$
is surjective. We have that
so by Proposition 2.6 we have that
![]() $G_{0}(\mathcal {U}_{0})_{\mathcal {I}}=0.$
Thus,
$G_{0}(\mathcal {U}_{0})_{\mathcal {I}}=0.$
Thus,
 $$ \begin{align} p_{*}q^{*}: K_{0}\left(D_{\text{sg}}(\mathcal{Z}_{0})\right)_{\mathcal{I}}\xrightarrow{\sim} K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right)_{\mathcal{I}}. \end{align} $$
$$ \begin{align} p_{*}q^{*}: K_{0}\left(D_{\text{sg}}(\mathcal{Z}_{0})\right)_{\mathcal{I}}\xrightarrow{\sim} K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right)_{\mathcal{I}}. \end{align} $$
Let
![]() $x\in K_{0}\left (D_{\text {sg}}(\mathcal {Z}_{0})\right )$
. Let e be the Euler class of the vector bundle
$x\in K_{0}\left (D_{\text {sg}}(\mathcal {Z}_{0})\right )$
. Let e be the Euler class of the vector bundle
![]() $q:\mathcal {S}\to \mathcal {Z}$
. Then e divides
$q:\mathcal {S}\to \mathcal {Z}$
. Then e divides
 $e^{\prime }:=\prod _{\beta \in S}\left (1-q^{\beta }\right )$
. By the assumption
$e^{\prime }:=\prod _{\beta \in S}\left (1-q^{\beta }\right )$
. By the assumption
![]() $f|_{\mathcal {S}}=q^{*}\left (f|_{\mathcal {Z}}\right )$
, we have that
$f|_{\mathcal {S}}=q^{*}\left (f|_{\mathcal {Z}}\right )$
, we have that
The factors of e are in the set
![]() $\mathcal {I}$
, so (10) implies that
$\mathcal {I}$
, so (10) implies that
 $$ \begin{align*}\iota_{*}:=p_{*}t_{*}: K_{0}\left(D_{\text{sg}}(\mathcal{Z}_{0})\right)_{\mathcal{I}}\xrightarrow{\sim} K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right)_{\mathcal{I}}.\end{align*} $$
$$ \begin{align*}\iota_{*}:=p_{*}t_{*}: K_{0}\left(D_{\text{sg}}(\mathcal{Z}_{0})\right)_{\mathcal{I}}\xrightarrow{\sim} K_{0}\left(D_{\text{sg}}(\mathcal{X}_{0})\right)_{\mathcal{I}}.\end{align*} $$
The last statement follows from
![]() $\iota ^{*}\iota _{*}$
being multiplication by
$\iota ^{*}\iota _{*}$
being multiplication by
![]() $e^{\prime }$
and using that the factors of
$e^{\prime }$
and using that the factors of
![]() $e^{\prime }$
are in
$e^{\prime }$
are in
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Remark. Via the restriction maps, Proposition 2.4 and Theorem 2.5 also hold for open substacks of
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
3 The Hall algebra
3.1 Definition of the Hall algebra
Let
![]() $(Q,W)$
be a quiver with potential. For
$(Q,W)$
be a quiver with potential. For
![]() $d\in \mathbb {N}^{I}$
, consider the stack of representations
$d\in \mathbb {N}^{I}$
, consider the stack of representations
with regular function
![]() $\text {Tr}(W):\mathcal {X}(d)\to \mathbb {A}^{1}_{\mathbb {C}};$
see Subsection 2.1 for more details. For
$\text {Tr}(W):\mathcal {X}(d)\to \mathbb {A}^{1}_{\mathbb {C}};$
see Subsection 2.1 for more details. For
![]() $d,e\in \mathbb {N}^{I}$
two dimension vectors, consider the stack
$d,e\in \mathbb {N}^{I}$
two dimension vectors, consider the stack
of pairs of representations
![]() $ A\subset B$
, where A has dimension d and B has dimension
$ A\subset B$
, where A has dimension d and B has dimension
![]() $d+e$
. Let
$d+e$
. Let
![]() $\theta \in \mathbb {Q}^{I}$
be a King stability condition. Define the slope function:
$\theta \in \mathbb {Q}^{I}$
be a King stability condition. Define the slope function:
 $$ \begin{align*}\tau(d):=\frac{\sum_{i\in I}\theta^{i} d^{i}}{\sum_{i\in I} d^{i}}.\end{align*} $$
$$ \begin{align*}\tau(d):=\frac{\sum_{i\in I}\theta^{i} d^{i}}{\sum_{i\in I} d^{i}}.\end{align*} $$
For a fixed slope
![]() $\mu $
, let
$\mu $
, let
![]() $\Lambda _{\mu }\subset \mathbb {N}^{I}$
be the monoid of dimension vectors with slope
$\Lambda _{\mu }\subset \mathbb {N}^{I}$
be the monoid of dimension vectors with slope
![]() $\mu $
. We denote by
$\mu $
. We denote by
![]() $\mathcal {X}(d)^{\text {ss}}\subset \mathcal {X}(d)$
the substack of
$\mathcal {X}(d)^{\text {ss}}\subset \mathcal {X}(d)$
the substack of
![]() $\theta $
-semistable representations. There is a cocharacter
$\theta $
-semistable representations. There is a cocharacter
![]() $\lambda _{d,e}$
whose diagram of fixed and attracting loci (1) is
$\lambda _{d,e}$
whose diagram of fixed and attracting loci (1) is
 $$ \begin{align} \mathcal{X}(d)^{\text{ss}}\times \mathcal{X}(e)^{\text{ss}}\xleftarrow{q_{d,e}} \mathcal{X}(d,e)^{\text{ss}} \xrightarrow{p_{d,e}} \mathcal{X}(d+e)^{\text{ss}}. \end{align} $$
$$ \begin{align} \mathcal{X}(d)^{\text{ss}}\times \mathcal{X}(e)^{\text{ss}}\xleftarrow{q_{d,e}} \mathcal{X}(d,e)^{\text{ss}} \xrightarrow{p_{d,e}} \mathcal{X}(d+e)^{\text{ss}}. \end{align} $$
Fix such a cocharacter
![]() $\lambda _{d,e}$
. The induced regular functions are compatible with respect to these maps:
$\lambda _{d,e}$
. The induced regular functions are compatible with respect to these maps:
We use p and q instead of
![]() $p_{d,e}$
and
$p_{d,e}$
and
![]() $q_{d,e}$
when there is no danger of confusion.
$q_{d,e}$
when there is no danger of confusion.
For every edge
![]() $e\in E$
, let
$e\in E$
, let
![]() $\mathbb {C}^{*}$
act on
$\mathbb {C}^{*}$
act on
![]() $\text {Hom}\,(\mathbb {C}^{s(e)},\mathbb {C}^{t(e)})$
by scalar multiplication. We denote the product of these multiplicative groups by
$\text {Hom}\,(\mathbb {C}^{s(e)},\mathbb {C}^{t(e)})$
by scalar multiplication. We denote the product of these multiplicative groups by
![]() $(\mathbb {C}^{*})^{E}$
. The Hall algebras considered in this paper are equivariant with respect to a torus T such that
$(\mathbb {C}^{*})^{E}$
. The Hall algebras considered in this paper are equivariant with respect to a torus T such that
![]() $T\subset (\mathbb {C}^{*})^{E}$
and W is T-invariant. We say that
$T\subset (\mathbb {C}^{*})^{E}$
and W is T-invariant. We say that
![]() $(Q,W)$
satisfies Assumption A if there exists an extra
$(Q,W)$
satisfies Assumption A if there exists an extra
![]() $\mathbb {C}^{*}\subset (\mathbb {C}^{*})^{E}$
such that the regular functions
$\mathbb {C}^{*}\subset (\mathbb {C}^{*})^{E}$
such that the regular functions
![]() $\text {Tr}(W_{d})$
are all homogeneous of weight
$\text {Tr}(W_{d})$
are all homogeneous of weight
![]() $2$
. We consider graded categories of matrix factorizations with respect to such a fixed
$2$
. We consider graded categories of matrix factorizations with respect to such a fixed
![]() $\mathbb {C}^{*}$
. Different choices of such
$\mathbb {C}^{*}$
. Different choices of such
![]() $\mathbb {C}^{*}$
give different categories
$\mathbb {C}^{*}$
give different categories
![]() $\text {MF}^{\text {gr}}$
, but all these categories have the same Grothendieck group [Reference Toda36, Corollary 3.13].
$\text {MF}^{\text {gr}}$
, but all these categories have the same Grothendieck group [Reference Toda36, Corollary 3.13].
Consider the diagonal map
![]() $\delta : BT\to BT\times BT.$
There are induced maps
$\delta : BT\to BT\times BT.$
There are induced maps
Definition 3.1. Consider the functor
 $$ \begin{align*} m_{d,e} :=p_{*}q^{*}\,\text{TS}\,\delta^{*}: \text{MF}_{T}\left(\mathcal{X}(d)^{\text{ss}}, W_{d}\right) & \,\boxtimes\, \text{MF}_{T}\left(\mathcal{X}(e)^{\text{ss}}, W_{e}\right) \\[3pt] &\qquad\qquad\qquad\quad \to \text{MF}_{T}\left(\mathcal{X}(d+e)^{\text{ss}}, W_{d+e}\right), \end{align*} $$
$$ \begin{align*} m_{d,e} :=p_{*}q^{*}\,\text{TS}\,\delta^{*}: \text{MF}_{T}\left(\mathcal{X}(d)^{\text{ss}}, W_{d}\right) & \,\boxtimes\, \text{MF}_{T}\left(\mathcal{X}(e)^{\text{ss}}, W_{e}\right) \\[3pt] &\qquad\qquad\qquad\quad \to \text{MF}_{T}\left(\mathcal{X}(d+e)^{\text{ss}}, W_{d+e}\right), \end{align*} $$
where
![]() $\text {TS}$
is the Thom–Sebastiani functor; see Subsection 2.10. Under Assumption A, we consider the functor
$\text {TS}$
is the Thom–Sebastiani functor; see Subsection 2.10. Under Assumption A, we consider the functor
 $$ \begin{align*} m_{d,e}:=p_{*}q^{*}\,\text{TS}\,\delta^{*}: \text{MF}^{\text{gr}}_{T}\left(\mathcal{X}(d)^{\text{ss}}, W_{d}\right) & \,\boxtimes\, \text{MF}^{\text{gr}}_{T}\left(\mathcal{X}(e)^{\text{ss}}, W_{e}\right) \\[3pt] &\qquad\qquad\qquad\quad \rightarrow \text{MF}^{\text{gr}}_{T}\left(\mathcal{X}(d+e)^{\text{ss}}, W_{d+e}\right).\end{align*} $$
$$ \begin{align*} m_{d,e}:=p_{*}q^{*}\,\text{TS}\,\delta^{*}: \text{MF}^{\text{gr}}_{T}\left(\mathcal{X}(d)^{\text{ss}}, W_{d}\right) & \,\boxtimes\, \text{MF}^{\text{gr}}_{T}\left(\mathcal{X}(e)^{\text{ss}}, W_{e}\right) \\[3pt] &\qquad\qquad\qquad\quad \rightarrow \text{MF}^{\text{gr}}_{T}\left(\mathcal{X}(d+e)^{\text{ss}}, W_{d+e}\right).\end{align*} $$
Definition 3.2. Consider the
![]() $\Lambda _{\mu }$
-graded category
$\Lambda _{\mu }$
-graded category
 $$ \begin{align*}\text{HA}_{T}(Q,W)_{\mu}:=\bigoplus_{d\in\Lambda_{\mu}} \text{MF}_{T}\left(\mathcal{X}(d)^{\text{ss}}, W_{d}\right).\end{align*} $$
$$ \begin{align*}\text{HA}_{T}(Q,W)_{\mu}:=\bigoplus_{d\in\Lambda_{\mu}} \text{MF}_{T}\left(\mathcal{X}(d)^{\text{ss}}, W_{d}\right).\end{align*} $$
Under Assumption A, we consider the
![]() $\Lambda _{\mu }$
-graded category
$\Lambda _{\mu }$
-graded category
 $$ \begin{align*}\text{HA}^{\text{gr}}_{T}(Q,W)_{\mu}:=\bigoplus_{d\in\Lambda_{\mu}} \text{MF}^{\text{gr}}_{T}\left(\mathcal{X}(d)^{\text{ss}}, W_{d}\right).\end{align*} $$
$$ \begin{align*}\text{HA}^{\text{gr}}_{T}(Q,W)_{\mu}:=\bigoplus_{d\in\Lambda_{\mu}} \text{MF}^{\text{gr}}_{T}\left(\mathcal{X}(d)^{\text{ss}}, W_{d}\right).\end{align*} $$
We call these categories the categorical Hall algebras of
![]() $(Q,W)$
. We call the Grothendieck group of these categories the K-theoretic Hall algebras of
$(Q,W)$
. We call the Grothendieck group of these categories the K-theoretic Hall algebras of
![]() $(Q,W)$
.
$(Q,W)$
.
In this section, we prove Theorem 1.1 and its version for graded matrix factorizations:
Theorem 3.3. The categories
![]() $\text {HA}_{T}(Q,W)_{\mu }$
and
$\text {HA}_{T}(Q,W)_{\mu }$
and
![]() $\text {HA}^{\text {gr}}_{T}(Q,W)_{\mu }$
are monoidal with respect to the multiplication functors m.
$\text {HA}^{\text {gr}}_{T}(Q,W)_{\mu }$
are monoidal with respect to the multiplication functors m.
Proof. We discuss the statement for
![]() $\text {MF}$
, the one for
$\text {MF}$
, the one for
![]() $\text {MF}^{\text {gr}}$
follows in the same way. Let
$\text {MF}^{\text {gr}}$
follows in the same way. Let
![]() $d, e, f\in \Lambda _{\mu }$
. Let
$d, e, f\in \Lambda _{\mu }$
. Let
![]() $\mathcal {X}(d,e,f)$
be the stacks of triples of representations of Q
$\mathcal {X}(d,e,f)$
be the stacks of triples of representations of Q
with A of dimension d,
![]() $B/A$
of dimension e and
$B/A$
of dimension e and
![]() $C/B$
of dimension f. We use the shorthand notations
$C/B$
of dimension f. We use the shorthand notations
 $$ \begin{align*} \textbf{C}_{T}(d)&:=\text{MF}\left(\mathcal{X}(d)^{\text{ss}}, W_{d}\right),\\[3pt] \textbf{C}_{T}(d,e)&:=\text{MF}\left(\mathcal{X}(d,e)^{\text{ss}}, W_{d+e}\right),\\[3pt] \textbf{C}_{T}(d,e,f)&:=\text{MF}\left(\mathcal{X}(d,e,f)^{\text{ss}}, W_{d+e+f}\right)\,\text{, etc.} \end{align*} $$
$$ \begin{align*} \textbf{C}_{T}(d)&:=\text{MF}\left(\mathcal{X}(d)^{\text{ss}}, W_{d}\right),\\[3pt] \textbf{C}_{T}(d,e)&:=\text{MF}\left(\mathcal{X}(d,e)^{\text{ss}}, W_{d+e}\right),\\[3pt] \textbf{C}_{T}(d,e,f)&:=\text{MF}\left(\mathcal{X}(d,e,f)^{\text{ss}}, W_{d+e+f}\right)\,\text{, etc.} \end{align*} $$
We also use the shorthand notation
![]() $\mathcal {X}_{T}(d)=\mathcal {X}(d)/T$
. We need to show that the following diagram commutes:
$\mathcal {X}_{T}(d)=\mathcal {X}(d)/T$
. We need to show that the following diagram commutes:

where we abused notation and dropped
![]() $\text {TS}$
from the notation of the morphisms. The Thom–Sebastiani functor commutes with the pullbacks and pushforwards above. For the upper right corner, the maps are induced from the ones of the Cartesian diagram
$\text {TS}$
from the notation of the morphisms. The Thom–Sebastiani functor commutes with the pullbacks and pushforwards above. For the upper right corner, the maps are induced from the ones of the Cartesian diagram

and one can use proper base change to deduce that
![]() $p_{2*}q_{1}^{*}\delta ^{*}=q_{d,e+f}^{*}\delta ^{*} p_{e,f*}$
. A similar argument shows that the lower left corner commutes. The lower right corner clearly commutes. For the upper left corner of diagram (12), consider the diagram
$p_{2*}q_{1}^{*}\delta ^{*}=q_{d,e+f}^{*}\delta ^{*} p_{e,f*}$
. A similar argument shows that the lower left corner commutes. The lower right corner clearly commutes. For the upper left corner of diagram (12), consider the diagram

where we have slightly abused notation involving the maps above. The upper left corner of (13) clearly commutes. The upper right and lower left corners are base-change diagrams. The lower right corner of (13) commutes because all maps are base change of the map
along the maps in the Cartesian diagram

The diagram (13) commutes, and thus, diagram (12) commutes as well.
3.2 Comparison with the preprojective KHA
3.2.1
Consider a quiver
 $\widetilde {Q}=(I, \widetilde {E})$
and a decomposition of sets
$\widetilde {Q}=(I, \widetilde {E})$
and a decomposition of sets
![]() $\widetilde {E}=E^{d}\sqcup C$
. Let
$\widetilde {E}=E^{d}\sqcup C$
. Let
![]() $Q^{d}=(I,E^{d})$
and
$Q^{d}=(I,E^{d})$
and
![]() $Q^{\prime }=(I,C)$
. The group
$Q^{\prime }=(I,C)$
. The group
![]() $\mathbb {C}^{*}$
acts on representations of
$\mathbb {C}^{*}$
acts on representations of
![]() $\widetilde {Q}$
by scaling the linear maps corresponding to edges in C with weight
$\widetilde {Q}$
by scaling the linear maps corresponding to edges in C with weight
![]() $2$
. Consider a potential
$2$
. Consider a potential
![]() $\widetilde {W}$
of
$\widetilde {W}$
of
![]() $\widetilde {Q}$
on which
$\widetilde {Q}$
on which
![]() $\mathbb {C}^{*}$
acts with weight
$\mathbb {C}^{*}$
acts with weight
![]() $2$
. The set C is called a cut for
$2$
. The set C is called a cut for
 $(\widetilde{Q}, \widetilde{W})$
in the literature. Denote by
$(\widetilde{Q}, \widetilde{W})$
in the literature. Denote by
 $\widetilde {\mathcal {X}(a)}$
the moduli stack of representations of dimension a for the quiver
$\widetilde {\mathcal {X}(a)}$
the moduli stack of representations of dimension a for the quiver
![]() $\widetilde {Q}$
and by
$\widetilde {Q}$
and by
![]() $\mathcal {X}^{d}(a)=R^{d}(a)/G(a)$
the analogous stack for the quiver
$\mathcal {X}^{d}(a)=R^{d}(a)/G(a)$
the analogous stack for the quiver
![]() $Q^{d}$
. We consider the category of graded matrix factorizations
$Q^{d}$
. We consider the category of graded matrix factorizations
 $\text {MF}^{\text {gr}}(\widetilde {\mathcal {X}(a)}, \widetilde {W}_{a})$
with respect to the action of the group
$\text {MF}^{\text {gr}}(\widetilde {\mathcal {X}(a)}, \widetilde {W}_{a})$
with respect to the action of the group
![]() $\mathbb {C}^{*}$
mentioned above. Denote the representation space of
$\mathbb {C}^{*}$
mentioned above. Denote the representation space of
![]() $Q^{\prime }$
by
$Q^{\prime }$
by
![]() $C(a)$
. We abuse notation and denote by
$C(a)$
. We abuse notation and denote by
![]() $C(a)$
the natural vector bundle on
$C(a)$
the natural vector bundle on
![]() $\mathcal {X}^{d}(a)$
. Write
$\mathcal {X}^{d}(a)$
. Write
 $$ \begin{align*}\widetilde{W}=\sum_{c\in C}cW_{c},\end{align*} $$
$$ \begin{align*}\widetilde{W}=\sum_{c\in C}cW_{c},\end{align*} $$
where
![]() $W_{c}$
is a path of
$W_{c}$
is a path of
![]() $Q^{d}$
. Define the algebra
$Q^{d}$
. Define the algebra
 $$ \begin{align*}P:=\mathbb{C}\left[Q^{d}\right]/\mathcal{J},\end{align*} $$
$$ \begin{align*}P:=\mathbb{C}\left[Q^{d}\right]/\mathcal{J},\end{align*} $$
where
![]() $\mathcal {J}$
is the two-sided ideal generated by
$\mathcal {J}$
is the two-sided ideal generated by
![]() $W_{c}$
for
$W_{c}$
for
![]() $c\in C$
. The potential
$c\in C$
. The potential
![]() $\widetilde {W}$
induces a section
$\widetilde {W}$
induces a section
 $s\in \Gamma \left (\mathcal {X}^{d}(a), C(a)^{\vee }\right )$
, and thus a map
$s\in \Gamma \left (\mathcal {X}^{d}(a), C(a)^{\vee }\right )$
, and thus a map
![]() $\partial :C(a)\to \mathcal {O}_{\mathcal {X}^{d}(a)}$
. The corresponding regular function constructed in (8) is
$\partial :C(a)\to \mathcal {O}_{\mathcal {X}^{d}(a)}$
. The corresponding regular function constructed in (8) is
 $$ \begin{align*}\text{Tr}\,\widetilde{W}:\widetilde{\mathcal{X}(a)}\to\mathbb{A}^{1}_{\mathbb{C}}.\end{align*} $$
$$ \begin{align*}\text{Tr}\,\widetilde{W}:\widetilde{\mathcal{X}(a)}\to\mathbb{A}^{1}_{\mathbb{C}}.\end{align*} $$
The moduli stack of representations of P of dimension a is the Köszul stack
 $$ \begin{align} \mathfrak{P}(a):=\text{Spec}\left(\mathcal{O}_{R^{d}(a)}\left[C(a)[1];\partial\right]\right)\big/ G(a). \end{align} $$
$$ \begin{align} \mathfrak{P}(a):=\text{Spec}\left(\mathcal{O}_{R^{d}(a)}\left[C(a)[1];\partial\right]\right)\big/ G(a). \end{align} $$
By the dimensional reduction equivalence (9) (see also [Reference Davison4, Appendix A.3] for the argument in cohomology), we have an equivalence:
 $$ \begin{align} \Phi: D^{b}\left(\mathfrak{P}(a)\right)\cong \text{MF}^{\text{gr}}(\widetilde{\mathcal{X}(a)}, \widetilde{W}). \end{align} $$
$$ \begin{align} \Phi: D^{b}\left(\mathfrak{P}(a)\right)\cong \text{MF}^{\text{gr}}(\widetilde{\mathcal{X}(a)}, \widetilde{W}). \end{align} $$
3.2.2
Let
![]() $Q=(I,E)$
be a quiver, and consider the tripled quiver
$Q=(I,E)$
be a quiver, and consider the tripled quiver
 $(\widetilde{Q}, \widetilde{W})$
from Subsection 2.4.
$(\widetilde{Q}, \widetilde{W})$
from Subsection 2.4.
![]() $Q^{d}$
is the doubled quiver of Q. Let
$Q^{d}$
is the doubled quiver of Q. Let
![]() $C=\{\omega _{i}|\,i\in I\}$
. Then
$C=\{\omega _{i}|\,i\in I\}$
. Then
![]() $Q^{d}$
is the doubled quiver of Q. In this case, the ideal
$Q^{d}$
is the doubled quiver of Q. In this case, the ideal
![]() $\mathcal {J}$
is
$\mathcal {J}$
is
 $$ \begin{align*}\mathcal{J}=\left(\sum_{\substack{e\in E,\\[3pt] s(e)=i}}[\overline{e}, e], i\in I\right),\end{align*} $$
$$ \begin{align*}\mathcal{J}=\left(\sum_{\substack{e\in E,\\[3pt] s(e)=i}}[\overline{e}, e], i\in I\right),\end{align*} $$
so the algebra P is the preprojective algebra of Q, and thus,
![]() $\mathfrak {P}(a)$
is the stack of representation of P of dimension a. Consider the categorical preprojective Hall algebra studied by Varagnolo–Vasserot [Reference Varagnolo and Vasserot38]:
$\mathfrak {P}(a)$
is the stack of representation of P of dimension a. Consider the categorical preprojective Hall algebra studied by Varagnolo–Vasserot [Reference Varagnolo and Vasserot38]:
 $$ \begin{align*}\text{HA}_{T}(Q):=\bigoplus_{d\in\mathbb{N}^{I}}D^{b}_{T}\left(\mathfrak{P}(d)\right).\end{align*} $$
$$ \begin{align*}\text{HA}_{T}(Q):=\bigoplus_{d\in\mathbb{N}^{I}}D^{b}_{T}\left(\mathfrak{P}(d)\right).\end{align*} $$
We obtain an equivalence of Hall algebra categories
 $$ \begin{align*}\text{HA}_{T}(Q)\cong \text{HA}_{T}(\widetilde{Q}, \widetilde{W}).\end{align*} $$
$$ \begin{align*}\text{HA}_{T}(Q)\cong \text{HA}_{T}(\widetilde{Q}, \widetilde{W}).\end{align*} $$
3.2.3
Let
![]() $a,b,d\in \mathbb {N}^{I}$
with
$a,b,d\in \mathbb {N}^{I}$
with
![]() $d=a+b$
. We denote the multiplication maps for
$d=a+b$
. We denote the multiplication maps for
![]() $(a,b)$
for
$(a,b)$
for
![]() $\widetilde {Q}$
by
$\widetilde {Q}$
by
![]() $\widetilde {p}$
,
$\widetilde {p}$
,
![]() $\widetilde {q}$
and for
$\widetilde {q}$
and for
![]() $Q^{d}$
by p, q. Let
$Q^{d}$
by p, q. Let
![]() $\lambda $
be a cocharacter
$\lambda $
be a cocharacter
![]() $\lambda _{a,b}$
as in (11). Define the line bundle on
$\lambda _{a,b}$
as in (11). Define the line bundle on
 $\widetilde {\mathcal {X}(a)}\times \widetilde {\mathcal {X}(b)}$
:
$\widetilde {\mathcal {X}(a)}\times \widetilde {\mathcal {X}(b)}$
:
 $$ \begin{align} \omega_{a,b}:=\det (C(d)^{\lambda\leqslant 0}\big/C(d)^{\lambda}). \end{align} $$
$$ \begin{align} \omega_{a,b}:=\det (C(d)^{\lambda\leqslant 0}\big/C(d)^{\lambda}). \end{align} $$
We twist the multiplication
![]() $\widetilde {m}$
on
$\widetilde {m}$
on
 $\text {HA}_{T}(\widetilde{Q}, \widetilde{W})$
and define
$\text {HA}_{T}(\widetilde{Q}, \widetilde{W})$
and define
 $$ \begin{align*} \widetilde{m'}:=\widetilde{p}_{*}\widetilde{q}^{*}\left(-\otimes\omega_{a,b}\right)\,\text{TS}\,\delta^{*}: \text{MF}^{\text{gr}}_{T}(\widetilde{\mathcal{X}(a)}, \widetilde{W_{a}}) & \otimes \text{MF}^{\text{gr}}_{T}(\widetilde{\mathcal{X}(b)}, \widetilde{W_{b}})\\[3pt] &\qquad\qquad\qquad \to \text{MF}^{\text{gr}}_{T}(\widetilde{\mathcal{X}(d)}, \widetilde{W_{d}}). \end{align*} $$
$$ \begin{align*} \widetilde{m'}:=\widetilde{p}_{*}\widetilde{q}^{*}\left(-\otimes\omega_{a,b}\right)\,\text{TS}\,\delta^{*}: \text{MF}^{\text{gr}}_{T}(\widetilde{\mathcal{X}(a)}, \widetilde{W_{a}}) & \otimes \text{MF}^{\text{gr}}_{T}(\widetilde{\mathcal{X}(b)}, \widetilde{W_{b}})\\[3pt] &\qquad\qquad\qquad \to \text{MF}^{\text{gr}}_{T}(\widetilde{\mathcal{X}(d)}, \widetilde{W_{d}}). \end{align*} $$
Let m be the multiplication of the preprojective
![]() $\text {HA}_{T}(Q)$
. By a T-equivariant version of [Reference Pădurariu25, Proposition 2.2], the following diagram commutes:
$\text {HA}_{T}(Q)$
. By a T-equivariant version of [Reference Pădurariu25, Proposition 2.2], the following diagram commutes:

When passing to
![]() $K_{0}$
, the multiplication
$K_{0}$
, the multiplication
![]() $\widetilde {m^{\prime }}$
is conjugation of
$\widetilde {m^{\prime }}$
is conjugation of
![]() $\widetilde {m}$
by an explicit rational function; see [Reference Varagnolo and Vasserot38, Subsection 2.3.7].
$\widetilde {m}$
by an explicit rational function; see [Reference Varagnolo and Vasserot38, Subsection 2.3.7].
3.3 Examples of KHA
3.3.1 The potential zero case
Let Q be an arbitrary quiver. Let
![]() $i,i^{\prime }$
be vertices of Q, and let
$i,i^{\prime }$
be vertices of Q, and let
![]() $\{1,\cdots , \varepsilon (i,i^{\prime })\}$
be the set of edges from i to
$\{1,\cdots , \varepsilon (i,i^{\prime })\}$
be the set of edges from i to
![]() $i^{\prime }$
. Consider the action of
$i^{\prime }$
. Consider the action of
 $(\mathbb {C}^{*})^{\varepsilon (i,i^{\prime })}$
on
$(\mathbb {C}^{*})^{\varepsilon (i,i^{\prime })}$
on
![]() $R(d)$
whose jth copy acts on
$R(d)$
whose jth copy acts on
![]() $R(d)$
with weight
$R(d)$
with weight
![]() $1$
on the factor
$1$
on the factor
 $\text {Hom}\left (\mathbb {C}^{d_{s(j)}}, \mathbb {C}^{d_{t(j)}}\right )$
corresponding to the edge j. Denote by
$\text {Hom}\left (\mathbb {C}^{d_{s(j)}}, \mathbb {C}^{d_{t(j)}}\right )$
corresponding to the edge j. Denote by
![]() $q_{j}$
the weight corresponding to the jth copy of
$q_{j}$
the weight corresponding to the jth copy of
![]() $\mathbb {C}^{*}$
. Define
$\mathbb {C}^{*}$
. Define
 $$ \begin{align} \zeta_{ii^{\prime}}(z):= \frac{\left(1-q_{1}^{-1}z^{-1}\right)\cdots \left(1-q_{\varepsilon(i,i^{\prime})}^{-1}z^{-1}\right)}{\left(1-z^{-1}\right)^{\delta_{ii^{\prime}}}}, \end{align} $$
$$ \begin{align} \zeta_{ii^{\prime}}(z):= \frac{\left(1-q_{1}^{-1}z^{-1}\right)\cdots \left(1-q_{\varepsilon(i,i^{\prime})}^{-1}z^{-1}\right)}{\left(1-z^{-1}\right)^{\delta_{ii^{\prime}}}}, \end{align} $$
where
![]() $\delta _{ii^{\prime }}$
is
$\delta _{ii^{\prime }}$
is
![]() $1$
if
$1$
if
![]() $i=i^{\prime }$
and
$i=i^{\prime }$
and
![]() $0$
otherwise. Let T be a subtorus of
$0$
otherwise. Let T be a subtorus of
![]() $(\mathbb {C}^{*})^{E}$
which fixes W. We also use the notation
$(\mathbb {C}^{*})^{E}$
which fixes W. We also use the notation
![]() $q_{j}$
for the corresponding weight of T. For
$q_{j}$
for the corresponding weight of T. For
![]() $d\in \mathbb {N}^{I}$
, let
$d\in \mathbb {N}^{I}$
, let
![]() $\mathfrak {S}_{d}:=\times _{i\in I}\,\mathfrak {S}_{d_{i}}$
be the Weyl group of
$\mathfrak {S}_{d}:=\times _{i\in I}\,\mathfrak {S}_{d_{i}}$
be the Weyl group of
![]() $G(d)$
.
$G(d)$
.
Proposition 3.4. The
![]() $\mathbb {N}^{I}\!\!$
-graded vector space of
$\mathbb {N}^{I}\!\!$
-graded vector space of
![]() $\text {KHA}_{T}(Q,0)$
has d graded space
$\text {KHA}_{T}(Q,0)$
has d graded space
 $$ \begin{align*}K_{0}^{T}(\mathcal{X}(d))\cong K_{0}(BT)\left[z_{i,j}^{\pm 1}\right]^{\mathfrak{S}_{d}},\end{align*} $$
$$ \begin{align*}K_{0}^{T}(\mathcal{X}(d))\cong K_{0}(BT)\left[z_{i,j}^{\pm 1}\right]^{\mathfrak{S}_{d}},\end{align*} $$
where
![]() $i\in I$
and
$i\in I$
and
![]() $1\leqslant j\leqslant d_{i}$
. Let
$1\leqslant j\leqslant d_{i}$
. Let
![]() $f\in K_{0}^{T}(\mathcal {X}(a))$
,
$f\in K_{0}^{T}(\mathcal {X}(a))$
,
![]() $g\in K_{0}^{T}(\mathcal {X}(b))$
with
$g\in K_{0}^{T}(\mathcal {X}(b))$
with
![]() $a+b=d$
. Then the multiplication in
$a+b=d$
. Then the multiplication in
![]() $\text {KHA}_{T}(Q,0)$
is
$\text {KHA}_{T}(Q,0)$
is
 $$ \begin{align*}f\cdot g=\sum_{w\in \mathfrak{S}_{d}/\mathfrak{S}_{a}\times\mathfrak{S}_{b}} w\left(fg\prod_{\substack{i,i^{\prime}\in I\\[3pt] j\leqslant a_{i}\\[3pt] j^{\prime}>a_{i^{\prime}}}}\zeta_{ii^{\prime}}\left(\frac{z_{ij}}{z_{i^{\prime}j^{\prime}}}\right) \right).\end{align*} $$
$$ \begin{align*}f\cdot g=\sum_{w\in \mathfrak{S}_{d}/\mathfrak{S}_{a}\times\mathfrak{S}_{b}} w\left(fg\prod_{\substack{i,i^{\prime}\in I\\[3pt] j\leqslant a_{i}\\[3pt] j^{\prime}>a_{i^{\prime}}}}\zeta_{ii^{\prime}}\left(\frac{z_{ij}}{z_{i^{\prime}j^{\prime}}}\right) \right).\end{align*} $$
Proof. Consider the maps
 $$ \begin{align*} \iota_{a,b}&:R(a,b)/G(a,b)\hookrightarrow R(d)/G(a,b)\\[3pt] \pi_{a,b}&:R(d)/G(a,b)\to \mathcal{X}(d). \end{align*} $$
$$ \begin{align*} \iota_{a,b}&:R(a,b)/G(a,b)\hookrightarrow R(d)/G(a,b)\\[3pt] \pi_{a,b}&:R(d)/G(a,b)\to \mathcal{X}(d). \end{align*} $$
The multiplication is defined by the composition
 $$ \begin{align*}\mathcal{X}(a)\times\mathcal{X}(b)\xrightarrow{q_{a,b}^{*}} \mathcal{X}(a,b)\xrightarrow{\iota_{a,b*}} R(d)/G(a,b)\xrightarrow{\pi_{a,b*}} \mathcal{X}(d).\end{align*} $$
$$ \begin{align*}\mathcal{X}(a)\times\mathcal{X}(b)\xrightarrow{q_{a,b}^{*}} \mathcal{X}(a,b)\xrightarrow{\iota_{a,b*}} R(d)/G(a,b)\xrightarrow{\pi_{a,b*}} \mathcal{X}(d).\end{align*} $$
The pullback map is an isomorphism
 $$ \begin{align} q_{a,b}^{*}:K_{0}^{T}(\mathcal{X}(a)\times\mathcal{X}(b))\cong K_{0}^{T}(\mathcal{X}(a,b)). \end{align} $$
$$ \begin{align} q_{a,b}^{*}:K_{0}^{T}(\mathcal{X}(a)\times\mathcal{X}(b))\cong K_{0}^{T}(\mathcal{X}(a,b)). \end{align} $$
Let N be the normal bundle of the map
![]() $\iota _{a,b}$
. The weights of
$\iota _{a,b}$
. The weights of
![]() $N^{\vee }$
are
$N^{\vee }$
are
 $q^{-1}_{e}z_{ij}^{-1}z_{i^{\prime }j^{\prime }}$
, where
$q^{-1}_{e}z_{ij}^{-1}z_{i^{\prime }j^{\prime }}$
, where
![]() $j\leqslant a_{i}$
,
$j\leqslant a_{i}$
,
![]() $j^{\prime }>a_{i^{\prime }}$
, and
$j^{\prime }>a_{i^{\prime }}$
, and
![]() $e\in \{1,\cdots ,\varepsilon (i,i^{\prime })\}$
is an edge between i and
$e\in \{1,\cdots ,\varepsilon (i,i^{\prime })\}$
is an edge between i and
![]() $i^{\prime }$
. For
$i^{\prime }$
. For
![]() $h\in K_{0}^{T}(\mathcal {X}(a,b))$
, we thus have that
$h\in K_{0}^{T}(\mathcal {X}(a,b))$
, we thus have that
 $$ \begin{align} \iota_{a,b*}(h)=h\prod_{\substack{i,i^{\prime}\in I\\[3pt] j\leqslant a_{i}\\[3pt] j^{\prime}>a_{i^{\prime}}}}\left(1-q_{1}^{-1} z_{ij}^{-1}z_{i^{\prime}j^{\prime}}\right)\cdots (1-q_{\varepsilon(i,i^{\prime})}^{-1} z_{ij}^{-1}z_{i^{\prime}j^{\prime}}). \end{align} $$
$$ \begin{align} \iota_{a,b*}(h)=h\prod_{\substack{i,i^{\prime}\in I\\[3pt] j\leqslant a_{i}\\[3pt] j^{\prime}>a_{i^{\prime}}}}\left(1-q_{1}^{-1} z_{ij}^{-1}z_{i^{\prime}j^{\prime}}\right)\cdots (1-q_{\varepsilon(i,i^{\prime})}^{-1} z_{ij}^{-1}z_{i^{\prime}j^{\prime}}). \end{align} $$
Further, for
![]() $h\in K_{0}^{T}(R(d)/G(a,b))$
, we have that
$h\in K_{0}^{T}(R(d)/G(a,b))$
, we have that
 $$ \begin{align} \pi_{a,b*}(h)=\sum_{w\in\mathfrak{S}_{d}/\mathfrak{S}_{a}\times\mathfrak{S}_{b}} w\left(\frac{h}{\prod_{\substack{i\in I\\[3pt] j\leqslant a_{i}<k}}\left(1-z_{ij}^{-1}z_{ik}\right)}\right); \end{align} $$
$$ \begin{align} \pi_{a,b*}(h)=\sum_{w\in\mathfrak{S}_{d}/\mathfrak{S}_{a}\times\mathfrak{S}_{b}} w\left(\frac{h}{\prod_{\substack{i\in I\\[3pt] j\leqslant a_{i}<k}}\left(1-z_{ij}^{-1}z_{ik}\right)}\right); \end{align} $$
see, for example, [Reference Yang and Zhao39, Proposition 1.2 or the proof of Proposition 2.3]. The formula for the multiplication of the
![]() $\text {KHA}_{T}(Q,0)$
follows from (19), (20), and (21).
$\text {KHA}_{T}(Q,0)$
follows from (19), (20), and (21).
A shuffle formula for the product of
![]() $\text {CoHA}$
appears in [Reference Kontsevich and Soibelman16, Section 2.4] and for a general oriented cohomological theory in [Reference Yang and Zhao39].
$\text {CoHA}$
appears in [Reference Kontsevich and Soibelman16, Section 2.4] and for a general oriented cohomological theory in [Reference Yang and Zhao39].
Proposition 3.4 implies that:
Corollary 3.5. Let J be Jordan quiver. Consider the action of
![]() $\mathbb {C}^{*}$
which scales representations of J with weight
$\mathbb {C}^{*}$
which scales representations of J with weight
![]() $1$
. There is an isomorphism
$1$
. There is an isomorphism
 $$ \begin{align*}\text{KHA}_{\mathbb{C}^{*}}(J,0)\cong U_{q}^{>}(L\mathfrak{sl}_{2}).\end{align*} $$
$$ \begin{align*}\text{KHA}_{\mathbb{C}^{*}}(J,0)\cong U_{q}^{>}(L\mathfrak{sl}_{2}).\end{align*} $$
Proof. The dimension d graded component of
![]() $\text {KHA}_{\mathbb {C}^{*}}(J,0)$
is
$\text {KHA}_{\mathbb {C}^{*}}(J,0)$
is
 $$ \begin{align*}K_{0}^{\mathbb{C}^{*}}(\mathcal{X}(d))= \mathbb{Z}\left[q^{\pm 1}\right]\left[z_{1}^{\pm 1},\cdots, z_{d}^{\pm 1}\right]^{\mathfrak{S}_{d}}.\end{align*} $$
$$ \begin{align*}K_{0}^{\mathbb{C}^{*}}(\mathcal{X}(d))= \mathbb{Z}\left[q^{\pm 1}\right]\left[z_{1}^{\pm 1},\cdots, z_{d}^{\pm 1}\right]^{\mathfrak{S}_{d}}.\end{align*} $$
In this case,
 $$ \begin{align*}\zeta(z)=\frac{1-q^{-1}z^{-1}}{1-z^{-1}}.\end{align*} $$
$$ \begin{align*}\zeta(z)=\frac{1-q^{-1}z^{-1}}{1-z^{-1}}.\end{align*} $$
Consider dimension vectors
![]() $a,b,d\in \mathbb {N}$
such that
$a,b,d\in \mathbb {N}$
such that
![]() $a+b=d$
. The multiplication of
$a+b=d$
. The multiplication of
![]() $f\in K_{0}^{\mathbb {C}^{*}}(\mathcal {X}(a))$
and
$f\in K_{0}^{\mathbb {C}^{*}}(\mathcal {X}(a))$
and
![]() $g\in K_{0}^{\mathbb {C}^{*}}(\mathcal {X}(b))$
is
$g\in K_{0}^{\mathbb {C}^{*}}(\mathcal {X}(b))$
is
 $$ \begin{align*}(f\cdot g)(z_{1},\cdots, z_{d})=\sum_{\mathfrak{S}_{d}/\mathfrak{S}_{a}\times\mathfrak{S}_{b}} \left(f\left(z_{1},\cdots, z_{a}\right)g\left(z_{a+1},\cdots, z_{d}\right)\prod_{\substack{1\leqslant i\leqslant a,\\[3pt] a+1\leqslant j\leqslant d}} \zeta\left(\frac{z_{i}}{z_{j}}\right)\right).\end{align*} $$
$$ \begin{align*}(f\cdot g)(z_{1},\cdots, z_{d})=\sum_{\mathfrak{S}_{d}/\mathfrak{S}_{a}\times\mathfrak{S}_{b}} \left(f\left(z_{1},\cdots, z_{a}\right)g\left(z_{a+1},\cdots, z_{d}\right)\prod_{\substack{1\leqslant i\leqslant a,\\[3pt] a+1\leqslant j\leqslant d}} \zeta\left(\frac{z_{i}}{z_{j}}\right)\right).\end{align*} $$
By [Reference Tsymbaliuk37, Theorem 3.5], the quantum group
![]() $U_{q}^{>}(L\mathfrak {sl}_{2})$
has the same shuffle product description.
$U_{q}^{>}(L\mathfrak {sl}_{2})$
has the same shuffle product description.
3.3.2
Let
![]() $(Q,W)$
be an arbitrary quiver with potential, and let T be a torus preserving the potential W.
$(Q,W)$
be an arbitrary quiver with potential, and let T be a torus preserving the potential W.
Proposition 3.6. Assume that
![]() $R(d)^{T(d)\times T}$
is in the zero locus of
$R(d)^{T(d)\times T}$
is in the zero locus of
![]() $\text {Tr}\left (W_{d}\right )$
. The inclusion
$\text {Tr}\left (W_{d}\right )$
. The inclusion
![]() $\iota _{d}:\mathcal {X}(d)_{0}\to \mathcal {X}(d)$
induces an algebra morphism
$\iota _{d}:\mathcal {X}(d)_{0}\to \mathcal {X}(d)$
induces an algebra morphism
Proof. First, the morphism
![]() $\iota _{d*}: D^{b}_{T}(\mathcal {X}(d)_{0})\to D^{b}_{T}(\mathcal {X}(d))$
commutes with the maps used in the definition of multiplication. The attracting maps for the category of singularities are induced from
$\iota _{d*}: D^{b}_{T}(\mathcal {X}(d)_{0})\to D^{b}_{T}(\mathcal {X}(d))$
commutes with the maps used in the definition of multiplication. The attracting maps for the category of singularities are induced from
 $$ \begin{align*}(\mathcal{X}(a)\times\mathcal{X}(b))_{0}\xleftarrow{q}\mathcal{X}(a,b)_{0}\xrightarrow{p}\mathcal{X}(d)_{0}.\end{align*} $$
$$ \begin{align*}(\mathcal{X}(a)\times\mathcal{X}(b))_{0}\xleftarrow{q}\mathcal{X}(a,b)_{0}\xrightarrow{p}\mathcal{X}(d)_{0}.\end{align*} $$
Let
![]() $a,b,d\in \mathbb {N}^{I}$
with
$a,b,d\in \mathbb {N}^{I}$
with
![]() $d=a+b$
. For this, we need to check that the following diagram is commutative:
$d=a+b$
. For this, we need to check that the following diagram is commutative:

where
![]() $i:\mathcal {X}(a)_{0}\times \mathcal {X}(b)_{0}\to \mathcal {X}(d)_{0}$
. Recall that
$i:\mathcal {X}(a)_{0}\times \mathcal {X}(b)_{0}\to \mathcal {X}(d)_{0}$
. Recall that
![]() $i_{*}$
is the Thom–Sebastiani functor. It is enough to show that the following diagram commutes:
$i_{*}$
is the Thom–Sebastiani functor. It is enough to show that the following diagram commutes:

The left corner commutes from proper base change. The right corner clearly commutes.
We next show that
![]() $\iota _{d*}\, K^{T}_{0}(\mathcal {X}(d)_{0})=0$
. By Propositions 2.3 and 2.5, the restriction map is an isomorphism
$\iota _{d*}\, K^{T}_{0}(\mathcal {X}(d)_{0})=0$
. By Propositions 2.3 and 2.5, the restriction map is an isomorphism
 $$ \begin{align*}K_{0}^{T}(\mathcal{X}(d))_{\mathcal{I}}\xrightarrow{\sim} K_{0}^{T(d)\times T}(R(d)^{T(d)\times T})_{\mathcal{I}},\end{align*} $$
$$ \begin{align*}K_{0}^{T}(\mathcal{X}(d))_{\mathcal{I}}\xrightarrow{\sim} K_{0}^{T(d)\times T}(R(d)^{T(d)\times T})_{\mathcal{I}},\end{align*} $$
where
![]() ${\mathcal {I}}$
is the set in Proposition 2.5. The map
${\mathcal {I}}$
is the set in Proposition 2.5. The map
![]() $K_{0}^{T}(\mathcal {X}(d))\hookrightarrow K_{0}^{T}(\mathcal {X}(d))_{\mathcal {I}}$
is injective. By the assumption on
$K_{0}^{T}(\mathcal {X}(d))\hookrightarrow K_{0}^{T}(\mathcal {X}(d))_{\mathcal {I}}$
is injective. By the assumption on
![]() $(Q,W)$
and T, the map
$(Q,W)$
and T, the map
 $R(d)^{T\times T(d)}\big /T(d)\hookrightarrow \mathcal {X}(d)$
factors through
$R(d)^{T\times T(d)}\big /T(d)\hookrightarrow \mathcal {X}(d)$
factors through
 $$ \begin{align*}R(d)^{T\times T(d)}\big/T(d)\hookrightarrow \mathcal{X}(d)_{0}\hookrightarrow \mathcal{X}(d).\end{align*} $$
$$ \begin{align*}R(d)^{T\times T(d)}\big/T(d)\hookrightarrow \mathcal{X}(d)_{0}\hookrightarrow \mathcal{X}(d).\end{align*} $$
The following map is thus injective:
For any complex F in
![]() $\text {Perf}\,(\mathcal {X}(d)_{0})$
, we have an exact triangle
$\text {Perf}\,(\mathcal {X}(d)_{0})$
, we have an exact triangle
 $$ \begin{align*}F[1]\to\iota_{d}^{*}\iota_{d*}(F)\to F\xrightarrow{[1]};\end{align*} $$
$$ \begin{align*}F[1]\to\iota_{d}^{*}\iota_{d*}(F)\to F\xrightarrow{[1]};\end{align*} $$
see [Reference Halpern-Leistner and Pomerleano12, Remark 1.8], so
![]() $\iota _{d}^{*}\iota _{d*}(F)=0$
in
$\iota _{d}^{*}\iota _{d*}(F)=0$
in
![]() $K_{0}^{T}(\mathcal {X}(d)_{0})$
. Thus, the map
$K_{0}^{T}(\mathcal {X}(d)_{0})$
. Thus, the map
factors through
The induced maps
![]() $K^{T}_{0}\left (D_{\text {sg}}(\mathcal {X}(d)_{0})\right )\to K^{T}_{0}(\mathcal {X}(d))$
respect multiplication by (22), so
$K^{T}_{0}\left (D_{\text {sg}}(\mathcal {X}(d)_{0})\right )\to K^{T}_{0}(\mathcal {X}(d))$
respect multiplication by (22), so
is an algebra morphism.
Remark. Let Q be a quiver. Consider the tripled quiver
 $(\widetilde{Q}, \widetilde{W})$
. Using (2), (17) and Proposition 3.6, we obtain an algebra morphism from the preprojective KHA of Q to a shuffle algebra
$(\widetilde{Q}, \widetilde{W})$
. Using (2), (17) and Proposition 3.6, we obtain an algebra morphism from the preprojective KHA of Q to a shuffle algebra
 $$ \begin{align*}\text{KHA}_{T}(Q)\cong \text{KHA}^{\text{gr}}_{T}(\widetilde{Q}, \widetilde{W})\cong \text{KHA}_{T}(\widetilde{Q}, \widetilde{W}) \to \text{KHA}_{T}(\widetilde{Q}, 0).\end{align*} $$
$$ \begin{align*}\text{KHA}_{T}(Q)\cong \text{KHA}^{\text{gr}}_{T}(\widetilde{Q}, \widetilde{W})\cong \text{KHA}_{T}(\widetilde{Q}, \widetilde{W}) \to \text{KHA}_{T}(\widetilde{Q}, 0).\end{align*} $$
This allows for explicit computations in preprojective KHAs in conjunction with generation results and allows for checking Conjecture 1.2 in particular cases. The most general result in this direction is due to Varagnolo–Vasserot [Reference Varagnolo and Vasserot38], who checked the conjecture for finite and affine type quiver except
 $A_{1}^{(1)}$
.
$A_{1}^{(1)}$
.
4 Representations of KHA
4.1
Let
![]() $(Q^{\prime },W^{\prime })$
be a quiver with potential, let T be a torus as in Section 3.1 and let
$(Q^{\prime },W^{\prime })$
be a quiver with potential, let T be a torus as in Section 3.1 and let
![]() $\theta ^{\prime }\in \mathbb {Q}^{I^{\prime }}$
be a stability condition for
$\theta ^{\prime }\in \mathbb {Q}^{I^{\prime }}$
be a stability condition for
![]() $Q^{\prime }$
. Denote by
$Q^{\prime }$
. Denote by
![]() $\tau $
the slope function. Let
$\tau $
the slope function. Let
![]() $Q\subset Q^{\prime }$
be a subquiver with
$Q\subset Q^{\prime }$
be a subquiver with
![]() $I^{\prime }\setminus I=\{ \infty \}$
, and denote by
$I^{\prime }\setminus I=\{ \infty \}$
, and denote by
 $$ \begin{align*} W&:=W^{\prime}|_{Q},\\[3pt] \theta&:=\theta^{\prime}|_{Q}. \end{align*} $$
$$ \begin{align*} W&:=W^{\prime}|_{Q},\\[3pt] \theta&:=\theta^{\prime}|_{Q}. \end{align*} $$
Fix
![]() $\mu $
a slope for
$\mu $
a slope for
![]() $(Q, \theta )$
. Let
$(Q, \theta )$
. Let
![]() $d\in \Lambda _{\mu }$
be a dimension vector of Q. For any dimension vector
$d\in \Lambda _{\mu }$
be a dimension vector of Q. For any dimension vector
![]() $d\in \mathbb {N}^{I}$
, consider the dimension vectors
$d\in \mathbb {N}^{I}$
, consider the dimension vectors
 $$ \begin{align*} \widetilde{d}&:=(1,d),\\[3pt] d^{o}&:=(0,d) \end{align*} $$
$$ \begin{align*} \widetilde{d}&:=(1,d),\\[3pt] d^{o}&:=(0,d) \end{align*} $$
of
![]() $Q^{\prime }$
, where we identify
$Q^{\prime }$
, where we identify
![]() $\mathbb {N}\times \mathbb {N}^{I}\cong \mathbb {N}^{I^{\prime }}$
. We denote by
$\mathbb {N}\times \mathbb {N}^{I}\cong \mathbb {N}^{I^{\prime }}$
. We denote by
![]() $\mathcal {X}$
the moduli stacks for
$\mathcal {X}$
the moduli stacks for
![]() $Q^{\prime }$
. Then
$Q^{\prime }$
. Then
![]() $\mathcal {X}\left (d^{o}\right )$
is the moduli stack of representations of Q. We say that
$\mathcal {X}\left (d^{o}\right )$
is the moduli stack of representations of Q. We say that
![]() $\left (Q^{\prime }, Q, \theta ^{\prime }, \mu \right )$
satisfies Assumption B if
$\left (Q^{\prime }, Q, \theta ^{\prime }, \mu \right )$
satisfies Assumption B if
for
![]() $0<\varepsilon \ll 1$
. Then, for any
$0<\varepsilon \ll 1$
. Then, for any
![]() $d\in \Lambda _{\mu }$
, we have that
$d\in \Lambda _{\mu }$
, we have that
 $$ \begin{align*}\mu=\tau\left(d^{o}\right)<\tau(\widetilde{d}{\kern1pt})=\mu+\varepsilon^{\prime}\end{align*} $$
$$ \begin{align*}\mu=\tau\left(d^{o}\right)<\tau(\widetilde{d}{\kern1pt})=\mu+\varepsilon^{\prime}\end{align*} $$
for
![]() $0<\varepsilon ^{\prime }\ll 1$
. Let
$0<\varepsilon ^{\prime }\ll 1$
. Let
![]() $d,e\in \Lambda _{\mu }$
. Denote by
$d,e\in \Lambda _{\mu }$
. Denote by
![]() $\mathcal {X}\left (d^{o}, \widetilde{e}{\kern1pt}\right)^{\text {ss}}$
the stack of pairs
$\mathcal {X}\left (d^{o}, \widetilde{e}{\kern1pt}\right)^{\text {ss}}$
the stack of pairs
![]() $A\subset B$
such that A is
$A\subset B$
such that A is
![]() $\theta $
-semistable of dimension
$\theta $
-semistable of dimension
![]() $d^{o}$
and B is
$d^{o}$
and B is
![]() $\theta ^{\prime }$
-semistable of dimension
$\theta ^{\prime }$
-semistable of dimension
![]() $\widetilde {d+e}$
. Then
$\widetilde {d+e}$
. Then
![]() $B/A$
is
$B/A$
is
![]() $\theta ^{\prime }$
-semistable of dimension
$\theta ^{\prime }$
-semistable of dimension
![]() $\widetilde {e}$
, and A is
$\widetilde {e}$
, and A is
![]() $\theta ^{\prime }$
-semistable. There are maps
$\theta ^{\prime }$
-semistable. There are maps
 $$ \begin{align*} t_{d,e}&:\mathcal{X}\left(d^{o}, \widetilde{e}{\kern1pt}\right)^{\text{ss}}\to \mathcal{X}\left( d^{o}\right)^{\text{ss}}\times \mathcal{X}( \widetilde{e}{\kern1pt})^{\text{ss}},\\[3pt] s_{d,e}&:\mathcal{X}\left(d^{o}, \widetilde{e}{\kern1pt}\right)^{\text{ss}}\to \mathcal{X}( \widetilde{d+e})^{\text{ss}}. \end{align*} $$
$$ \begin{align*} t_{d,e}&:\mathcal{X}\left(d^{o}, \widetilde{e}{\kern1pt}\right)^{\text{ss}}\to \mathcal{X}\left( d^{o}\right)^{\text{ss}}\times \mathcal{X}( \widetilde{e}{\kern1pt})^{\text{ss}},\\[3pt] s_{d,e}&:\mathcal{X}\left(d^{o}, \widetilde{e}{\kern1pt}\right)^{\text{ss}}\to \mathcal{X}( \widetilde{d+e})^{\text{ss}}. \end{align*} $$
The map
![]() $t_{d,e}$
is an affine bundle map, and the map
$t_{d,e}$
is an affine bundle map, and the map
![]() $s_{d,e}$
is proper; see also the discussion in [Reference Soibelman32, Subsection 4.1]. Denote by
$s_{d,e}$
is proper; see also the discussion in [Reference Soibelman32, Subsection 4.1]. Denote by
 $$ \begin{align*}\text{R}_{T}\left(Q^{\prime},W^{\prime}\right)_{\mu}:=\bigoplus_{d\in\Lambda_{\mu}} \text{MF}^{\text{gr}}_{T}(\mathcal{X}(\widetilde{d}{\kern1pt}), W).\end{align*} $$
$$ \begin{align*}\text{R}_{T}\left(Q^{\prime},W^{\prime}\right)_{\mu}:=\bigoplus_{d\in\Lambda_{\mu}} \text{MF}^{\text{gr}}_{T}(\mathcal{X}(\widetilde{d}{\kern1pt}), W).\end{align*} $$
We denote its Grothendieck group by
 $\text {KR}_{T}\left (Q^{\prime },W^{\prime }\right )_{\mu }$
.
$\text {KR}_{T}\left (Q^{\prime },W^{\prime }\right )_{\mu }$
.
Proposition 4.1. In the above framework and under Assumption B,
![]() $\text {KHA}_{T}(Q,W)_{\mu }$
naturally acts on
$\text {KHA}_{T}(Q,W)_{\mu }$
naturally acts on
 $\text {KR}_{T}\left (Q^{\prime },W^{\prime }\right )_{\mu }$
via the functors
$\text {KR}_{T}\left (Q^{\prime },W^{\prime }\right )_{\mu }$
via the functors
 $$ \begin{align} p_{d,e*}q_{d,e}^{*}\,\text{TS}\,\delta: \text{MF}_{T}\left( \mathcal{X}\left(d^{o}\right)^{\text{ss}}, W\right) & \otimes \text{MF}_{T}\left(\mathcal{X}(\widetilde{e}{\kern1pt})^{\text{ss}}, W\right) \nonumber \\[3pt] &\qquad\qquad\qquad\quad \to \text{MF}_{T}(\mathcal{X}(\widetilde{d+e})^{\text{ss}}, W)\end{align} $$
$$ \begin{align} p_{d,e*}q_{d,e}^{*}\,\text{TS}\,\delta: \text{MF}_{T}\left( \mathcal{X}\left(d^{o}\right)^{\text{ss}}, W\right) & \otimes \text{MF}_{T}\left(\mathcal{X}(\widetilde{e}{\kern1pt})^{\text{ss}}, W\right) \nonumber \\[3pt] &\qquad\qquad\qquad\quad \to \text{MF}_{T}(\mathcal{X}(\widetilde{d+e})^{\text{ss}}, W)\end{align} $$
for
![]() $d,e\in \Lambda _{\mu }$
. If Assumption A is satisfied, we can consider graded categories
$d,e\in \Lambda _{\mu }$
. If Assumption A is satisfied, we can consider graded categories
![]() $\text {MF}^{\text {gr}}$
, and the analogous statement holds in that case as well.
$\text {MF}^{\text {gr}}$
, and the analogous statement holds in that case as well.
Proof. Same proof as in Theorem 3.3 works here.
4.2
Let
![]() $Q_{3}$
be the quiver with one vertex
$Q_{3}$
be the quiver with one vertex
![]() $0$
and three loops
$0$
and three loops
![]() $x,y,z,$
consider the potential
$x,y,z,$
consider the potential
![]() $W_{3}=xyz-xzy$
and consider the zero stability condition. Let
$W_{3}=xyz-xzy$
and consider the zero stability condition. Let
 $Q_{3}^{f}=\left (I^{f}, E^{f}\right )$
be the quiver with
$Q_{3}^{f}=\left (I^{f}, E^{f}\right )$
be the quiver with
![]() $I^{f}=\{0, \infty \}$
and
$I^{f}=\{0, \infty \}$
and
![]() $E^{f}=\{x,y,z,t\}$
. Consider the stability condition
$E^{f}=\{x,y,z,t\}$
. Consider the stability condition
![]() $\theta $
of
$\theta $
of
![]() $Q^{f}$
from Subsection 2.3. For
$Q^{f}$
from Subsection 2.3. For
![]() $d\in \mathbb {N}$
, denote by
$d\in \mathbb {N}$
, denote by
 $\widetilde {d}=(1,d)$
a dimension vector of
$\widetilde {d}=(1,d)$
a dimension vector of
![]() $Q^{f}$
. Assumption B is satisfied in this case by the construction of
$Q^{f}$
. Assumption B is satisfied in this case by the construction of
![]() $\theta $
. Let
$\theta $
. Let
![]() $T\subset (\mathbb {C}^{*})^{3}$
be a torus which fixes W. Consider the regular function
$T\subset (\mathbb {C}^{*})^{3}$
be a torus which fixes W. Consider the regular function
 $$ \begin{align*}\text{Tr}(W_{3,\widetilde{d}}): \mathcal{X}(\widetilde{d}{\kern1pt})^{\text{ss}}\to\mathbb{A}^{1}_{\mathbb{C}}.\end{align*} $$
$$ \begin{align*}\text{Tr}(W_{3,\widetilde{d}}): \mathcal{X}(\widetilde{d}{\kern1pt})^{\text{ss}}\to\mathbb{A}^{1}_{\mathbb{C}}.\end{align*} $$
Its critical locus is
 $\text {Hilb}\left (\mathbb {C}^{3},d\right )$
. Use the notation
$\text {Hilb}\left (\mathbb {C}^{3},d\right )$
. Use the notation
 $$ \begin{align*}K_{\text{crit}, T}(\text{Hilb}(\mathbb{A}^{3}_{\mathbb{C}}, d)):=K_{0}(\text{MF}_{T}(\mathcal{X}(\widetilde{d}{\kern1pt})^{\text{ss}}, W_{3,\widetilde{d}})).\end{align*} $$
$$ \begin{align*}K_{\text{crit}, T}(\text{Hilb}(\mathbb{A}^{3}_{\mathbb{C}}, d)):=K_{0}(\text{MF}_{T}(\mathcal{X}(\widetilde{d}{\kern1pt})^{\text{ss}}, W_{3,\widetilde{d}})).\end{align*} $$
Proposition 4.1 constructs an action of
![]() $\text {KHA}_{T}\left (Q_{3},W_{3}\right )$
on
$\text {KHA}_{T}\left (Q_{3},W_{3}\right )$
on
 $$ \begin{align*}\bigoplus_{d\geqslant 0}K_{\text{crit}, T}(\text{Hilb}(\mathbb{A}^{3}_{\mathbb{C}}, d)).\end{align*} $$
$$ \begin{align*}\bigoplus_{d\geqslant 0}K_{\text{crit}, T}(\text{Hilb}(\mathbb{A}^{3}_{\mathbb{C}}, d)).\end{align*} $$
4.3
We explain how Proposition 4.1 can be used to construct representations on K-theory of Nakajima quiver varieties following the analogous construction in cohomology [Reference Davison5, Section 6.3.]. Given a quiver
![]() $Q=(I,E)$
and
$Q=(I,E)$
and
![]() $f\in \mathbb {N}^{I}$
, denote by
$f\in \mathbb {N}^{I}$
, denote by
![]() $Q^{f}$
the framed quiver with vertices
$Q^{f}$
the framed quiver with vertices
![]() $I\cup \{\infty \}$
and
$I\cup \{\infty \}$
and
![]() $f_{i}$
new edges from
$f_{i}$
new edges from
![]() $\infty $
to
$\infty $
to
![]() $i\in I$
. Recall from Subsection 2.4 the construction of the double quiver
$i\in I$
. Recall from Subsection 2.4 the construction of the double quiver
![]() $\overline {Q}$
and tripled quiver with potential
$\overline {Q}$
and tripled quiver with potential
 $(\widetilde{Q}, \widetilde{W})$
. Let
$(\widetilde{Q}, \widetilde{W})$
. Let
![]() $\theta =0$
be the zero stability condition for Q. Consider the stability condition
$\theta =0$
be the zero stability condition for Q. Consider the stability condition
![]() $\theta ^{f}$
defined in Subsection 2.3 for the quiver
$\theta ^{f}$
defined in Subsection 2.3 for the quiver
![]() $Q^{f}$
.
$Q^{f}$
.
Define the torus
![]() $T^{\prime }\cong (\mathbb {C}^{*})^{E}$
, where for
$T^{\prime }\cong (\mathbb {C}^{*})^{E}$
, where for
![]() $e\in E$
the corresponding
$e\in E$
the corresponding
![]() $\mathbb {C}^{*}$
acts with weight
$\mathbb {C}^{*}$
acts with weight
![]() $1$
on the linear map corresponding to e, with weight
$1$
on the linear map corresponding to e, with weight
![]() $-1$
on the linear map corresponding to
$-1$
on the linear map corresponding to
![]() $\overline {e}$
and with weight
$\overline {e}$
and with weight
![]() $0$
on
$0$
on
![]() $\omega _{i}$
for any
$\omega _{i}$
for any
![]() $i\in I$
. We consider a torus
$i\in I$
. We consider a torus
![]() $T\subset T^{\prime }$
.
$T\subset T^{\prime }$
.
For
![]() $d\in \mathbb {N}^{I}$
, denote by
$d\in \mathbb {N}^{I}$
, denote by
 $\widetilde {d}=(1,d)\in \mathbb {N}\times \mathbb {N}^{I}$
. Consider the map that forgets the action of
$\widetilde {d}=(1,d)\in \mathbb {N}\times \mathbb {N}^{I}$
. Consider the map that forgets the action of
![]() $\omega _{i}$
:
$\omega _{i}$
:
 $$ \begin{align*}\pi: \mathcal{X}(\widetilde{Q^{f}},\widetilde{d}{\kern1pt})\to \mathcal{X}(\overline{Q^{f}},\widetilde{d}{\kern1pt}).\end{align*} $$
$$ \begin{align*}\pi: \mathcal{X}(\widetilde{Q^{f}},\widetilde{d}{\kern1pt})\to \mathcal{X}(\overline{Q^{f}},\widetilde{d}{\kern1pt}).\end{align*} $$
Observe that the doubled and tripled quivers considered above are for
![]() $Q^{f}$
. Ben Davison showed in [Reference Davison5, Lemma 6.5.] that the inclusion
$Q^{f}$
. Ben Davison showed in [Reference Davison5, Lemma 6.5.] that the inclusion
 $$ \begin{align*}\pi^{-1}(\mathcal{X}(\overline{Q^{f}},\widetilde{d}{\kern1pt})^{\text{ss}})\hookrightarrow \mathcal{X}(\widetilde{Q^{f}},\widetilde{d}{\kern1pt})^{\text{ss}}\end{align*} $$
$$ \begin{align*}\pi^{-1}(\mathcal{X}(\overline{Q^{f}},\widetilde{d}{\kern1pt})^{\text{ss}})\hookrightarrow \mathcal{X}(\widetilde{Q^{f}},\widetilde{d}{\kern1pt})^{\text{ss}}\end{align*} $$
induces an equality
 $$ \begin{align} \pi^{-1}(\mathcal{X}(\overline{Q^{f}},\widetilde{d}{\kern1pt})^{\text{ss}})\cap \text{crit}\,(\text{Tr}\,\widetilde{W^{f}})= \mathcal{X}(\widetilde{Q^{f}},\widetilde{d}{\kern1pt})^{\text{ss}}\cap \text{crit}\,(\text{Tr}\,\widetilde{W^{f}}).\end{align} $$
$$ \begin{align} \pi^{-1}(\mathcal{X}(\overline{Q^{f}},\widetilde{d}{\kern1pt})^{\text{ss}})\cap \text{crit}\,(\text{Tr}\,\widetilde{W^{f}})= \mathcal{X}(\widetilde{Q^{f}},\widetilde{d}{\kern1pt})^{\text{ss}}\cap \text{crit}\,(\text{Tr}\,\widetilde{W^{f}}).\end{align} $$
We consider the extra
![]() $\mathbb {C}^{*}$
-action induced by acting with weight
$\mathbb {C}^{*}$
-action induced by acting with weight
![]() $2$
on the linear maps corresponding to
$2$
on the linear maps corresponding to
![]() $\omega _{i}$
for
$\omega _{i}$
for
![]() $i\in I$
and with weight
$i\in I$
and with weight
![]() $0$
on the other linear maps. We consider
$0$
on the other linear maps. We consider
![]() $\text {MF}^{\text {gr}}$
with respect to this
$\text {MF}^{\text {gr}}$
with respect to this
![]() $\mathbb {C}^{*}$
-action. The equality (24) implies that
$\mathbb {C}^{*}$
-action. The equality (24) implies that
 $$ \begin{align*}\text{MF}^{\text{gr}}(\mathcal{X}(\widetilde{Q^{f}},\widetilde{d}{\kern1pt})^{\text{ss}}, W)\cong \text{MF}^{\text{gr}}(\pi^{-1}(\mathcal{X}(\overline{Q^{f}},\widetilde{d}{\kern1pt})^{\text{ss}}), W).\end{align*} $$
$$ \begin{align*}\text{MF}^{\text{gr}}(\mathcal{X}(\widetilde{Q^{f}},\widetilde{d}{\kern1pt})^{\text{ss}}, W)\cong \text{MF}^{\text{gr}}(\pi^{-1}(\mathcal{X}(\overline{Q^{f}},\widetilde{d}{\kern1pt})^{\text{ss}}), W).\end{align*} $$
Consider the stack
 $\mathcal {Y}:=\mathcal {X}(\overline {Q^{f}},\widetilde {d})^{\text {ss}}$
, the
$\mathcal {Y}:=\mathcal {X}(\overline {Q^{f}},\widetilde {d})^{\text {ss}}$
, the
 $\mathfrak {g}(\widetilde{d}{\kern1pt})$
-vector bundle
$\mathfrak {g}(\widetilde{d}{\kern1pt})$
-vector bundle
![]() $\pi ^{-1}\left (\mathcal {Y}\right )$
and the regular function
$\pi ^{-1}\left (\mathcal {Y}\right )$
and the regular function
![]() $\text {Tr}\,W_{\widetilde {d}}$
. We also denote the vector bundle by
$\text {Tr}\,W_{\widetilde {d}}$
. We also denote the vector bundle by
 $\mathfrak {g}(\widetilde{d}{\kern1pt})$
. The potential is constructed as in Subsection 2.11 via the section
$\mathfrak {g}(\widetilde{d}{\kern1pt})$
. The potential is constructed as in Subsection 2.11 via the section
![]() $s\in \Gamma \left (\mathcal {Y}, \mathfrak {g}(d)\right )$
corresponding to the natural moment map
$s\in \Gamma \left (\mathcal {Y}, \mathfrak {g}(d)\right )$
corresponding to the natural moment map
 $$ \begin{align*}s: T^{*}R(\widetilde{d}{\kern1pt})\cong \overline{R(\widetilde{d}{\kern1pt})}\to \mathfrak{g}(\widetilde{d}{\kern1pt}).\end{align*} $$
$$ \begin{align*}s: T^{*}R(\widetilde{d}{\kern1pt})\cong \overline{R(\widetilde{d}{\kern1pt})}\to \mathfrak{g}(\widetilde{d}{\kern1pt}).\end{align*} $$
It induces a map
 $\partial : \mathfrak {g}(\widetilde{d}{\kern1pt})\to \mathcal {O}_{\overline {R(\widetilde{d}{\kern1pt})}}$
. The diagonal
$\partial : \mathfrak {g}(\widetilde{d}{\kern1pt})\to \mathcal {O}_{\overline {R(\widetilde{d}{\kern1pt})}}$
. The diagonal
 $\mathbb {C}^{*}\hookrightarrow G(\widetilde{d}{\kern1pt})$
acts trivially on
$\mathbb {C}^{*}\hookrightarrow G(\widetilde{d}{\kern1pt})$
acts trivially on
 $\overline {R(\widetilde{d}{\kern1pt})}$
and
$\overline {R(\widetilde{d}{\kern1pt})}$
and
 $G(\widetilde{d}{\kern1pt})\big /\mathbb {C}^{*}\cong G(d)$
. Define
$G(\widetilde{d}{\kern1pt})\big /\mathbb {C}^{*}\cong G(d)$
. Define

Using dimensional reduction (see Subsections 2.11 and 3.2.1), we have that
 $$ \begin{align*}\text{MF}^{\text{gr}}_{T}\left(\pi^{-1}\left(\mathcal{Y}\right), W\right)\cong D^{b}_{T}(\mathfrak{P}(\widetilde{d}{\kern1pt})^{\text{ss}}).\end{align*} $$
$$ \begin{align*}\text{MF}^{\text{gr}}_{T}\left(\pi^{-1}\left(\mathcal{Y}\right), W\right)\cong D^{b}_{T}(\mathfrak{P}(\widetilde{d}{\kern1pt})^{\text{ss}}).\end{align*} $$
The moment map equations for
![]() $i\in I$
are the relations for the Nakajima quiver varieties
$i\in I$
are the relations for the Nakajima quiver varieties
![]() $N(f,d)$
, and the moment map equation for
$N(f,d)$
, and the moment map equation for
![]() $\infty $
is superfluous [Reference Davison5, page 33]. This means that
$\infty $
is superfluous [Reference Davison5, page 33]. This means that
 $\mathfrak {P}(\widetilde{d}{\kern1pt})^{\text {ss}}\cong N(f,d)$
.
$\mathfrak {P}(\widetilde{d}{\kern1pt})^{\text {ss}}\cong N(f,d)$
.
Assumption B is satisfied for
 $(\widetilde {Q^{f}}, \widetilde {Q}, \theta ^{f}, 0)$
. By Proposition 4.1 and by the discussion in Subsection 3.2, the algebra
$(\widetilde {Q^{f}}, \widetilde {Q}, \theta ^{f}, 0)$
. By Proposition 4.1 and by the discussion in Subsection 3.2, the algebra
 $\text {KHA}_{T}(Q)\cong \text {KHA}_{T}^{\text {gr}}(\widetilde{Q}, \widetilde{W})$
acts on
$\text {KHA}_{T}(Q)\cong \text {KHA}_{T}^{\text {gr}}(\widetilde{Q}, \widetilde{W})$
acts on
 $$ \begin{align*}\bigoplus_{d\in \mathbb{N}^{I}} K_{0}^{T}\left(N(f,d)\right).\end{align*} $$
$$ \begin{align*}\bigoplus_{d\in \mathbb{N}^{I}} K_{0}^{T}\left(N(f,d)\right).\end{align*} $$
4.4
Let J be the Jordan quiver. Its tripled quiver is
![]() $(Q_{3},W_{3})$
. Consider
$(Q_{3},W_{3})$
. Consider
![]() $T\subset (\mathbb {C}^{*})^{3}$
which fixes
$T\subset (\mathbb {C}^{*})^{3}$
which fixes
![]() $W_{3}$
. We obtain an action of
$W_{3}$
. We obtain an action of
![]() $\text {KHA}_{T}(J)\cong \text {KHA}_{T}^{\text {gr}}\left (Q_{3},W_{3}\right )$
on
$\text {KHA}_{T}(J)\cong \text {KHA}_{T}^{\text {gr}}\left (Q_{3},W_{3}\right )$
on
 $$ \begin{align} \bigoplus_{d\geqslant 0} K^{T}_{0}\left(\text{Hilb}\left(\mathbb{A}^{2}_{\mathbb{C}},d\right)\right). \end{align} $$
$$ \begin{align} \bigoplus_{d\geqslant 0} K^{T}_{0}\left(\text{Hilb}\left(\mathbb{A}^{2}_{\mathbb{C}},d\right)\right). \end{align} $$
The algebra
![]() $\text {KHA}_{T}(J)$
has a subalgebra isomorphic to
$\text {KHA}_{T}(J)$
has a subalgebra isomorphic to
 $U_{q, t}^{>}(\widehat {\widehat {\mathfrak {gl}_{1}}})$
[Reference Schiffmann and Vasserot30], [Reference Neguţ19]. In [Reference Feigin and Tsymbaliuk8], [Reference Schiffmann and Vasserot30], the authors construct a representation of the full quantum group
$U_{q, t}^{>}(\widehat {\widehat {\mathfrak {gl}_{1}}})$
[Reference Schiffmann and Vasserot30], [Reference Neguţ19]. In [Reference Feigin and Tsymbaliuk8], [Reference Schiffmann and Vasserot30], the authors construct a representation of the full quantum group
 $U_{q, t}(\widehat {\widehat {\mathfrak {gl}_{1}}})$
on the vector space (25).
$U_{q, t}(\widehat {\widehat {\mathfrak {gl}_{1}}})$
on the vector space (25).
5 The wall-crossing theorem
5.1
Let
![]() $\theta \in \mathbb {Q}^{I}$
be a stability condition for Q, and define the slope
$\theta \in \mathbb {Q}^{I}$
be a stability condition for Q, and define the slope
 $$ \begin{align*}\tau(d)=\frac{\sum_{i\in I} \theta^{i}d^{i}}{\sum_{i\in I} d^{i}}.\end{align*} $$
$$ \begin{align*}\tau(d)=\frac{\sum_{i\in I} \theta^{i}d^{i}}{\sum_{i\in I} d^{i}}.\end{align*} $$
For any partition
![]() $\underline {d}=(d_{1},\cdots , d_{k})$
of d with
$\underline {d}=(d_{1},\cdots , d_{k})$
of d with
![]() $d_{i}\in \mathbb {N}^{I}$
, consider the maps
$d_{i}\in \mathbb {N}^{I}$
, consider the maps
 $$ \begin{align*}\times_{i=1}^{k}\mathcal{X}(d_{i})\xleftarrow{q_{\underline{d}}}\mathcal{X}(d_{1},\cdots, d_{k})\xrightarrow{p_{\underline{d}}}\mathcal{X}(d).\end{align*} $$
$$ \begin{align*}\times_{i=1}^{k}\mathcal{X}(d_{i})\xleftarrow{q_{\underline{d}}}\mathcal{X}(d_{1},\cdots, d_{k})\xrightarrow{p_{\underline{d}}}\mathcal{X}(d).\end{align*} $$
The stack
![]() $\mathcal {X}(d)$
has a Harder–Narasimhan stratification with strata
$\mathcal {X}(d)$
has a Harder–Narasimhan stratification with strata
 $$ \begin{align*}p_{\underline{d}}(q_{\underline{d}}^{-1}(\times_{i=1}^{k}\mathcal{X}(d_{i})^{\text{ss}}))=:\mathcal{X}^{\prime}(\underline{d})\end{align*} $$
$$ \begin{align*}p_{\underline{d}}(q_{\underline{d}}^{-1}(\times_{i=1}^{k}\mathcal{X}(d_{i})^{\text{ss}}))=:\mathcal{X}^{\prime}(\underline{d})\end{align*} $$
corresponding to partitions
![]() $\underline {d}=(d_{1},\cdots ,d_{k})$
with
$\underline {d}=(d_{1},\cdots ,d_{k})$
with
![]() $k\geqslant 2$
,
$k\geqslant 2$
,
![]() $d_{i}$
nonzero for
$d_{i}$
nonzero for
![]() $1\leqslant i\leqslant k$
, and
$1\leqslant i\leqslant k$
, and
![]() $\mu _{1}>\cdots >\mu _{k}$
where
$\mu _{1}>\cdots >\mu _{k}$
where
![]() $\mu _{i}:=\tau (d_{i})$
.
$\mu _{i}:=\tau (d_{i})$
.
Let I be the set of such partitions. Consider two partitions
![]() $\underline {d}=(d_{1},\cdots , d_{k})$
and
$\underline {d}=(d_{1},\cdots , d_{k})$
and
![]() $\underline {e}=(e_{1},\cdots , e_{s})$
in I. We say that
$\underline {e}=(e_{1},\cdots , e_{s})$
in I. We say that
![]() $\underline {d}<\underline {e}$
if
$\underline {d}<\underline {e}$
if
![]() $k>s$
. Then
$k>s$
. Then
![]() $\mathcal {X}^{\prime }(\underline {d})$
with
$\mathcal {X}^{\prime }(\underline {d})$
with
![]() $\underline {d}\in I$
are a stratification as in Subsection 2.7.2.
$\underline {d}\in I$
are a stratification as in Subsection 2.7.2.
5.1.1
For
![]() $w\in \mathbb {Z}$
, let
$w\in \mathbb {Z}$
, let
![]() $D^{b}(\mathcal {X}(d))_{w}$
be the subcategory of
$D^{b}(\mathcal {X}(d))_{w}$
be the subcategory of
![]() $D^{b}(\mathcal {X}(d))$
of complexes on which the diagonal cocharacter
$D^{b}(\mathcal {X}(d))$
of complexes on which the diagonal cocharacter
![]() $\lambda :=z\cdot \text {Id}$
of
$\lambda :=z\cdot \text {Id}$
of
![]() $G(d)$
acts with weight w. The category
$G(d)$
acts with weight w. The category
![]() $D^{b}(\mathcal {X}(d))$
has an orthogonal decomposition in categories
$D^{b}(\mathcal {X}(d))$
has an orthogonal decomposition in categories
![]() $D^{b}(\mathcal {X}(d))_{w}$
for
$D^{b}(\mathcal {X}(d))_{w}$
for
![]() $w\in \mathbb {Z}$
.
$w\in \mathbb {Z}$
.
More generally, if
![]() $\mathcal {X}$
is a stack and T is a torus acting trivially on
$\mathcal {X}$
is a stack and T is a torus acting trivially on
![]() $\mathcal {X}$
, there is an orthogonal decomposition of
$\mathcal {X}$
, there is an orthogonal decomposition of
![]() $D^{b}_{T}(\mathcal {X})$
in categories
$D^{b}_{T}(\mathcal {X})$
in categories
![]() $D^{b}_{T}(\mathcal {X})_{\chi }$
, where
$D^{b}_{T}(\mathcal {X})_{\chi }$
, where
![]() $\chi $
is a weight of T and
$\chi $
is a weight of T and
![]() $D^{b}_{T}(\mathcal {X})_{\chi }$
is the subcategory of sheaves on
$D^{b}_{T}(\mathcal {X})_{\chi }$
is the subcategory of sheaves on
![]() $D^{b}_{T}(\mathcal {X})$
on which T acts with weight
$D^{b}_{T}(\mathcal {X})$
on which T acts with weight
![]() $\chi $
.
$\chi $
.
5.1.2
As a corollary of [Reference Halpern-Leistner11, Theorem 2.10, Amplification 2.11]—see the semiorthogonal decomposition (6)—we have that:
Proposition 5.1. The category
![]() $D^{b}(\mathcal {X}(d))$
has a semiorthogonal decomposition with summands
$D^{b}(\mathcal {X}(d))$
has a semiorthogonal decomposition with summands
 $$ \begin{align*}p_{\underline{d}*}q_{\underline{d}}^{*}( D^{b}(\times_{i=1}^{k}\mathcal{X}(d_{i})^{\text{ss}})_{\chi})\cong D^{b}(\times_{i=1}^{k}\mathcal{X}(d_{i})^{\text{ss}})_{\chi},\end{align*} $$
$$ \begin{align*}p_{\underline{d}*}q_{\underline{d}}^{*}( D^{b}(\times_{i=1}^{k}\mathcal{X}(d_{i})^{\text{ss}})_{\chi})\cong D^{b}(\times_{i=1}^{k}\mathcal{X}(d_{i})^{\text{ss}})_{\chi},\end{align*} $$
where
![]() $\underline {d}\in I$
and
$\underline {d}\in I$
and
![]() $\chi =(w_{1},\cdots ,w_{k})$
is a weight of
$\chi =(w_{1},\cdots ,w_{k})$
is a weight of
![]() $(\mathbb {C}^{*})^{k}$
. The analogous decomposition holds for
$(\mathbb {C}^{*})^{k}$
. The analogous decomposition holds for
![]() $D^{b}_{\mathbb {C}^{*}}(\mathcal {X}(d))$
where
$D^{b}_{\mathbb {C}^{*}}(\mathcal {X}(d))$
where
![]() $\mathbb {C}^{*}$
is a subgroup of
$\mathbb {C}^{*}$
is a subgroup of
![]() $(\mathbb {C}^{*})^{E}$
.
$(\mathbb {C}^{*})^{E}$
.
Using Propositions 2.1 and 2.2, we obtain the following corollary:
Corollary 5.2.
(a) The category
![]() $\text {MF}\left (\mathcal {X}(d), W\right )$
has a semiorthogonal decomposition with summands
$\text {MF}\left (\mathcal {X}(d), W\right )$
has a semiorthogonal decomposition with summands
 $$ \begin{align*}p_{\underline{d}*}q_{\underline{d}}^{*}(\text{MF}(\times_{i=1}^{k}\mathcal{X}^{\text{ss}}(d_{i}), W)_{\chi})\cong \text{MF}(\times_{i=1}^{k}\mathcal{X}^{\text{ss}}(d_{i}), W)_{\chi},\end{align*} $$
$$ \begin{align*}p_{\underline{d}*}q_{\underline{d}}^{*}(\text{MF}(\times_{i=1}^{k}\mathcal{X}^{\text{ss}}(d_{i}), W)_{\chi})\cong \text{MF}(\times_{i=1}^{k}\mathcal{X}^{\text{ss}}(d_{i}), W)_{\chi},\end{align*} $$
where
![]() $\underline {d}\in I$
and
$\underline {d}\in I$
and
![]() $\chi =(w_{1},\cdots , w_{k})$
is a weight of
$\chi =(w_{1},\cdots , w_{k})$
is a weight of
![]() $(\mathbb {C}^{*})^{k}$
.
$(\mathbb {C}^{*})^{k}$
.
(b) Assume that
![]() $(Q,W)$
satisfies Assumption A, and consider the corresponding
$(Q,W)$
satisfies Assumption A, and consider the corresponding
![]() $\text {MF}^{\text {gr}}$
. Then the category
$\text {MF}^{\text {gr}}$
. Then the category
![]() $\text {MF}^{\text {gr}}\left (\mathcal {X}(d), W\right )$
has a semiorthogonal decomposition with summands
$\text {MF}^{\text {gr}}\left (\mathcal {X}(d), W\right )$
has a semiorthogonal decomposition with summands
 $$ \begin{align*}p_{\underline{d}*}q_{\underline{d}}^{*}(\text{MF}^{\text{gr}}(\times_{i=1}^{k}\mathcal{X}(d_{i})^{\text{ss}}, W)_{\chi})\cong \text{MF}^{\text{gr}}(\times_{i=1}^{k}\mathcal{X}(d_{i})^{\text{ss}}, W)_{\chi},\end{align*} $$
$$ \begin{align*}p_{\underline{d}*}q_{\underline{d}}^{*}(\text{MF}^{\text{gr}}(\times_{i=1}^{k}\mathcal{X}(d_{i})^{\text{ss}}, W)_{\chi})\cong \text{MF}^{\text{gr}}(\times_{i=1}^{k}\mathcal{X}(d_{i})^{\text{ss}}, W)_{\chi},\end{align*} $$
where
![]() $\underline {d}\in I$
and
$\underline {d}\in I$
and
![]() $\chi =(w_{1},\cdots , w_{k})$
is a weight of
$\chi =(w_{1},\cdots , w_{k})$
is a weight of
![]() $(\mathbb {C}^{*})^{k}$
.
$(\mathbb {C}^{*})^{k}$
.
Proof. Let
![]() $\underline {d}\in I$
, and let
$\underline {d}\in I$
, and let
![]() $\chi $
be a weight as above. Let
$\chi $
be a weight as above. Let
![]() $\textbf {C}$
be a subcategory of
$\textbf {C}$
be a subcategory of
 $D^{b}\left (\times _{i=1}^{k}\mathcal {X}(d_{i})\right )_{\chi }$
on which
$D^{b}\left (\times _{i=1}^{k}\mathcal {X}(d_{i})\right )_{\chi }$
on which
![]() $p_{\underline {d}*}q_{\underline {d}}^{*}$
is fully faithful. Then
$p_{\underline {d}*}q_{\underline {d}}^{*}$
is fully faithful. Then
 $$ \begin{align*}\text{MF}(p_{\underline{d}*}q_{\underline{d}}^{*}\,\textbf{C}, W_{d})\cong p_{\underline{d}*}\text{MF}(q^{*}_{\underline{d}}\,\textbf{C}, p_{\underline{d}}^{*}W_{d})\cong p_{\underline{d}*}q_{\underline{d}}^{*}\,\text{MF}(\textbf{C}, \oplus_{i=1}^{k}W_{d_{i}}).\end{align*} $$
$$ \begin{align*}\text{MF}(p_{\underline{d}*}q_{\underline{d}}^{*}\,\textbf{C}, W_{d})\cong p_{\underline{d}*}\text{MF}(q^{*}_{\underline{d}}\,\textbf{C}, p_{\underline{d}}^{*}W_{d})\cong p_{\underline{d}*}q_{\underline{d}}^{*}\,\text{MF}(\textbf{C}, \oplus_{i=1}^{k}W_{d_{i}}).\end{align*} $$
The statement in part (a) follows from Proposition 2.1. The statement for
![]() $\text {MF}^{\text {gr}}$
follows similarly using Proposition 2.2.
$\text {MF}^{\text {gr}}$
follows similarly using Proposition 2.2.
5.1.3
We say that
![]() $(Q,W)$
satisfies Assumption C if. for all
$(Q,W)$
satisfies Assumption C if. for all
![]() $d,e\in \mathbb {N}^{I}$
and all stability conditions
$d,e\in \mathbb {N}^{I}$
and all stability conditions
![]() $\theta $
, the Thom–Sebastiani maps are isomorphisms:
$\theta $
, the Thom–Sebastiani maps are isomorphisms:
 $$ \begin{align*} \text{TS}:K_{0}\big(\text{MF}(\mathcal{X}(d)^{\text{ss}}, W_{d})\big) &\otimes K_{0}\big(\text{MF}(\mathcal{X}(e)^{\text{ss}}, W_{e})\big)\xrightarrow{\sim}\\[3pt] &\qquad\qquad\qquad\qquad K_{0}\big(\text{MF}(\mathcal{X}(d)^{\text{ss}}\times\mathcal{X}(e)^{\text{ss}}, W_{d}\oplus W_{e})\big). \end{align*} $$
$$ \begin{align*} \text{TS}:K_{0}\big(\text{MF}(\mathcal{X}(d)^{\text{ss}}, W_{d})\big) &\otimes K_{0}\big(\text{MF}(\mathcal{X}(e)^{\text{ss}}, W_{e})\big)\xrightarrow{\sim}\\[3pt] &\qquad\qquad\qquad\qquad K_{0}\big(\text{MF}(\mathcal{X}(d)^{\text{ss}}\times\mathcal{X}(e)^{\text{ss}}, W_{d}\oplus W_{e})\big). \end{align*} $$
Under Assumption A, we can formulate the analogous assumption for
![]() $\text {MF}^{\text {gr}}$
, which by [Reference Toda36, Corollary 3.13] is the same as the Assumption C above. Any pair
$\text {MF}^{\text {gr}}$
, which by [Reference Toda36, Corollary 3.13] is the same as the Assumption C above. Any pair
![]() $(Q,0)$
satisfies Assumption C. In [Reference Pădurariu24], we check that any tripled quiver
$(Q,0)$
satisfies Assumption C. In [Reference Pădurariu24], we check that any tripled quiver
 $(\widetilde{Q}, \widetilde{W})$
satisfies Assumption C.
$(\widetilde{Q}, \widetilde{W})$
satisfies Assumption C.
Theorem 5.3.
-
(a) Assume that
 $(Q,W)$
satisfies Assumption C. Let
$(Q,W)$
satisfies Assumption C. Let
 $\theta $
be a stability condition. There is an isomorphism of vector spaces
$\theta $
be a stability condition. There is an isomorphism of vector spaces  $$ \begin{align*}\text{KHA}(Q,W)\xrightarrow{\sim} \bigotimes_{\mu\in\mathbb{Q}} \text{KHA}(Q,W)_{\mu}.\end{align*} $$
$$ \begin{align*}\text{KHA}(Q,W)\xrightarrow{\sim} \bigotimes_{\mu\in\mathbb{Q}} \text{KHA}(Q,W)_{\mu}.\end{align*} $$
-
(b) Assume that
 $(Q,W)$
satisfies Assumptions A and C, and consider the corresponding
$(Q,W)$
satisfies Assumptions A and C, and consider the corresponding
 $\text {KHA}^{\text {gr}}$
. Let
$\text {KHA}^{\text {gr}}$
. Let
 $\theta $
be a stability condition. There is an isomorphism of vector spaces
$\theta $
be a stability condition. There is an isomorphism of vector spaces  $$ \begin{align*}\text{KHA}^{\text{gr}}(Q,W)\xrightarrow{\sim} \bigotimes_{\mu\in\mathbb{Q}} \text{KHA}^{\text{gr}}(Q,W)_{\mu}.\end{align*} $$
$$ \begin{align*}\text{KHA}^{\text{gr}}(Q,W)\xrightarrow{\sim} \bigotimes_{\mu\in\mathbb{Q}} \text{KHA}^{\text{gr}}(Q,W)_{\mu}.\end{align*} $$
The product on the right hand side on Theorem 5.3 is an ordered product taken after descending slopes; see also its analogue in cohomology [Reference Davison and Meinhardt6, Theorem B].
Proof. Let
![]() $d\in \mathbb {N}^{I}$
. We discuss the proof for part (a); part (b) follows from part (a). The statement follows from the isomorphism of vector spaces
$d\in \mathbb {N}^{I}$
. We discuss the proof for part (a); part (b) follows from part (a). The statement follows from the isomorphism of vector spaces
 $$ \begin{align} K_{0}\left(\text{MF}\left(\mathcal{X}(d), W\right)\right)\cong\bigoplus \bigotimes_{i=1}^{k} K_{0}\left(\text{MF}\left(\mathcal{X}(d_{i})^{\text{ss}}, W\right)\right), \end{align} $$
$$ \begin{align} K_{0}\left(\text{MF}\left(\mathcal{X}(d), W\right)\right)\cong\bigoplus \bigotimes_{i=1}^{k} K_{0}\left(\text{MF}\left(\mathcal{X}(d_{i})^{\text{ss}}, W\right)\right), \end{align} $$
where the sum is after all partitions
![]() $\underline {d}=(d_{1},\cdots ,d_{k})$
in I. For any
$\underline {d}=(d_{1},\cdots ,d_{k})$
in I. For any
![]() $d\in \mathbb {N}^{I}$
, there are decompositions
$d\in \mathbb {N}^{I}$
, there are decompositions
 $$ \begin{align*}K_{0}\left(\text{MF}\left(\mathcal{X}(d)^{\text{ss}}, W\right)\right)\cong\bigoplus_{w\in\mathbb{Z}}K_{0}\left(\text{MF}\left(\mathcal{X}(d)^{\text{ss}}, W\right)_{w}\right).\end{align*} $$
$$ \begin{align*}K_{0}\left(\text{MF}\left(\mathcal{X}(d)^{\text{ss}}, W\right)\right)\cong\bigoplus_{w\in\mathbb{Z}}K_{0}\left(\text{MF}\left(\mathcal{X}(d)^{\text{ss}}, W\right)_{w}\right).\end{align*} $$
The decomposition (26) now follows from Corollary 5.2 and the isomorphism from Assumption C.
5.2 Example
Let Q be a type A quiver with vertices labelled
![]() $1$
to n and edges from i to
$1$
to n and edges from i to
![]() $i+1$
for
$i+1$
for
![]() $1\leqslant i\leqslant n-1$
.
$1\leqslant i\leqslant n-1$
.
5.2.1
Consider first the stability condition
Denote by
![]() $\varepsilon _{i}$
the dimension vector with
$\varepsilon _{i}$
the dimension vector with
![]() $1$
in vertex i and zero everywhere else. The
$1$
in vertex i and zero everywhere else. The
![]() $\theta $
-semistable representations are at dimension vectors
$\theta $
-semistable representations are at dimension vectors
![]() $n\varepsilon _{i}$
for n a nonnegative integer. For
$n\varepsilon _{i}$
for n a nonnegative integer. For
![]() $1\leqslant i\leqslant n$
a vertex, let
$1\leqslant i\leqslant n$
a vertex, let
![]() $r_{i}$
be the unique representation of dimension
$r_{i}$
be the unique representation of dimension
![]() $\varepsilon _{i}$
. Then
$\varepsilon _{i}$
. Then
 $$ \begin{align*}\mathcal{X}(n\varepsilon_{i})^{\text{ss}}=\left(r_{i}^{\oplus n}\right)/ GL(n),\end{align*} $$
$$ \begin{align*}\mathcal{X}(n\varepsilon_{i})^{\text{ss}}=\left(r_{i}^{\oplus n}\right)/ GL(n),\end{align*} $$
so we have that
 $$ \begin{align*}S_{i}:=\bigoplus_{n\geqslant 0} K_{0}\left(\mathcal{X}(n\varepsilon_{i})^{\text{ss}}\right)\cong\bigoplus_{n\geqslant 0}K_{0}(BGL(n)).\end{align*} $$
$$ \begin{align*}S_{i}:=\bigoplus_{n\geqslant 0} K_{0}\left(\mathcal{X}(n\varepsilon_{i})^{\text{ss}}\right)\cong\bigoplus_{n\geqslant 0}K_{0}(BGL(n)).\end{align*} $$
As a corollary of Theorem 5.3, we obtain that:
Corollary 5.4.
![]() $\text {KHA}(Q, 0)$
is generated by the
$\text {KHA}(Q, 0)$
is generated by the
![]() $\varepsilon _{i}$
-graded pieces with
$\varepsilon _{i}$
-graded pieces with
![]() $1\leqslant i\leqslant n$
dimensional pieces under the multiplication map:
$1\leqslant i\leqslant n$
dimensional pieces under the multiplication map:
 $$ \begin{align*}\text{KHA}(Q, 0)\cong \bigotimes_{i=1}^{n} S_{i}.\end{align*} $$
$$ \begin{align*}\text{KHA}(Q, 0)\cong \bigotimes_{i=1}^{n} S_{i}.\end{align*} $$
5.2.2
Choose next the stability condition
The semistable representations are at the multiples of the roots
![]() $r_{1},\cdots , r_{N}$
of the Lie algebra associated to Q. Consider an algebra
$r_{1},\cdots , r_{N}$
of the Lie algebra associated to Q. Consider an algebra
 $S_{i}\cong \bigoplus _{n\geqslant 0}K_{0}(BGL(n))$
for any
$S_{i}\cong \bigoplus _{n\geqslant 0}K_{0}(BGL(n))$
for any
![]() $1\leqslant i\leqslant N$
. An analysis as above and Theorem 5.3 imply that:
$1\leqslant i\leqslant N$
. An analysis as above and Theorem 5.3 imply that:
Corollary 5.5. The
![]() $\text {KHA}(Q,0)$
is generated by the
$\text {KHA}(Q,0)$
is generated by the
![]() $r_{i}$
-graded pieces with
$r_{i}$
-graded pieces with
![]() $1\leqslant i\leqslant N$
under the multiplication map:
$1\leqslant i\leqslant N$
under the multiplication map:
 $$ \begin{align*}\text{KHA}(Q,0)\cong \bigotimes_{i=1}^{N} S_{i}.\end{align*} $$
$$ \begin{align*}\text{KHA}(Q,0)\cong \bigotimes_{i=1}^{N} S_{i}.\end{align*} $$
The analogues of Corollaries 5.4 and 5.5 for CoHA were proved by Rimanyi [Reference Rimanyi29]. The case of
![]() $A_{2}$
in cohomology has been treated by Kontsevich–Soibelman [Reference Kontsevich and Soibelman16, Section 2.8].
$A_{2}$
in cohomology has been treated by Kontsevich–Soibelman [Reference Kontsevich and Soibelman16, Section 2.8].
Acknowledgements
I would like to thank my PhD advisor Davesh Maulik for suggesting the problems discussed in the present paper and for his constant help and encouragement throughout the project. I would like to thank Ben Davison, Pavel Etingof, Daniel Halpern-Leistner, Andrei Neguţ, Andrei Okounkov, Yukinobu Toda and Eric Vasserot for useful conversations about the project. I thank the referees for many useful comments.
Competing Interests
None.