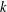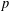2 results
16 - Interference, Diffraction, and Diffusion
-
- Book:
- Physics Behind Music
- Published online:
- 24 May 2023
- Print publication:
- 06 April 2023, pp 295-309
-
- Chapter
- Export citation
APPLICATIONS OF LERCH’S THEOREM TO PERMUTATIONS OF QUADRATIC RESIDUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 10 July 2019, pp. 362-371
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation