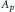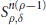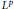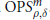In this paper we prove weighted norm inequalities with weights in the ${{A}_{p}}$ classes, for pseudodifferential operators with symbols in the class $S_{\rho ,\delta }^{n(\rho -1)}$ that fall outside the scope of Calderón–Zygmund theory. This is accomplished by controlling the sharp function of the pseudodifferential operator by Hardy–Littlewood type maximal functions. Our weighted norm inequalities also yield ${{L}^{p}}$ boundedness of commutators of functions of bounded mean oscillation with a wide class of operators in $\text{OPS}_{\rho ,\delta }^{m}$.

The algebra Ψ(M) of order zero pseudodifferential operators on a compact manifold M defines a well-known C*-extension of the algebra C(S*M) of continuous functions on the cospherical bundle S*M ⊂ T*M by the algebra К of compact operators. In his proof of the index theorem, Higson defined and used an asymptotic homomorphism T from C0(T*M) to К, which plays the role of a deformation for the commutative algebra C0(T*M). Similar constructions exist also for operators and symbols with coefficients in a C*-algebra. Recently we have shown that the image of the above extension under the Connes–Higson construction is T and that this extension can be reconstructed out of T. That is why the classical approach to the index theory coincides with the one based on asymptotic homomorphisms. But the image of the above extension is defined only outside the zero section of T*(M), so it may seem that the information encoded in the extension is not the same as that in the asymptotic homomorphism. We show that this is not the case.

We review basic notions and methods of noncommutative geometry and their applications to analysis and geometry on foliated manifolds.

We construct algebras of pseudodifferential operators on a continuous family groupoid $\mathcal{G}$ that are closed under holomorphic functional calculus, contain the algebra of all pseudodifferential operators of order 0 on $\mathcal{G}$ as a dense subalgebra and reflect the smooth structure of the groupoid $\mathcal{G}$, when $\mathcal{G}$ is smooth. As an application, we get a better understanding on the structure of inverses of elliptic pseudodifferential operators on classes of non-compact manifolds. For the construction of these algebras closed under holomorphic functional calculus, we develop three methods: one using semi-ideals, one using commutators and one based on Schwartz spaces on the groupoid.

One of our main results is to reduce the construction of spectrally invariant algebras of order 0 pseudodifferential operators to the analogous problem for regularizing operators. We then show that, in the case of the generalized ‘cusp’-calculi$c_n$, $n\ge2$, it is possible to construct algebras of regularizing operators that are closed under holomorphic functional calculus and consist of smooth kernels. For $n=1$, this was shown not to be possible by the first author in an earlier paper.

AMS 2000 Mathematics subject classification: Primary 35S05. Secondary 35J15; 47G30; 58J40; 46L87

On exhibe dans cette note une paramétrix (au sens faible) de l'opérateur sous-jacent à l'équation CFIE de l'électromagnétisme. L'intérêt de cetteparamétrix est de se prêter à différentes stratégies de discrétisationet ainsi de pouvoir être utilisée comme préconditionneur de la CFIE.On montre aussi que l'opérateur sous-jacent à la CFIE satisfait une conditionInf-Sup discrète uniforme, applicable aux espaces de discrétisation usuellement rencontrésen électromagnétisme, et qui permet d'établir un résultat inédit de convergencenumérique de la CFIE.