Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-04T19:30:33.677Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted Lp Boundedness of Pseudodifferential Operators and Applications

Published online by Cambridge University Press:  20 November 2018

Nicholas Michalowski ,
David J. Rule  and
Wolfgang Staubach
Nicholas Michalowski
Affiliation:
School of Mathematics and the Maxwell Institute of Mathematical Sciences, University of Edinburgh, Edinburgh, EH9 3JZ, Scotlande-mail: [email protected]
David J. Rule
Affiliation:
Department of Mathematics and the Maxwell Institute of Mathematical Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, Scotlande-mail: [email protected]: [email protected]
Wolfgang Staubach
Affiliation:
Department of Mathematics and the Maxwell Institute of Mathematical Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, Scotlande-mail: [email protected]: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

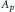In this paper we prove weighted norm inequalities with weights in the ${{A}_{p}}$ classes, for pseudodifferential operators with symbols in the class 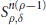$S_{\rho ,\delta }^{n(\rho -1)}$ that fall outside the scope of Calderón–Zygmund theory. This is accomplished by controlling the sharp function of the pseudodifferential operator by Hardy–Littlewood type maximal functions. Our weighted norm inequalities also yield 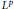${{L}^{p}}$ boundedness of commutators of functions of bounded mean oscillation with a wide class of operators in 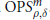$\text{OPS}_{\rho ,\delta }^{m}$.

Keywords

42B2042B2535S0547G30weighted norm inequalitypseudodifferential operatorcommutator estimates
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 3 , 01 September 2012 , pp. 555 - 570
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Álvarez, J. and Hounie, J., Estimates for the kernel and continuity properties of pseudo-differential operators. Ark. Mat. 28(1990), no. 1, 1–22. http://dx.doi.org/10.1007/BF02387364 Google Scholar
[2] Auscher, P. and Taylor, M., Paradifferential operators and commutator estimates. Comm. Partial Differential Equations 20(1995), no. 9–10, 1743–1775. http://dx.doi.org/10.1080/03605309508821150 Google Scholar
[3] Chanillo, S., Remarks on commutators of pseudo-differential operators. In: Multidimensional complex analysis and partial differential equations (São Carlos, 1995), Contemp. Math., 205, American Mathematical Society, Providence, RI, 1997, pp. 33–37.Google Scholar
[4] Chanillo, S. and Torchinsky, A., Sharp function and weighted Lp estimates for a class of pseudodifferential operators. Ark. Mat. 24(1986), no. 1, 1–25. http://dx.doi.org/10.1007/BF02384387 Google Scholar
[5] Coifman, R. R., Rochberg, R., and Weiss, G., Factorization theorems for Hardy spaces in several variables. Ann. of Math. (2) 103(1976), no. 3, 611–635. http://dx.doi.org/10.2307/1970954 Google Scholar
[6] Germain, P., Strong solutions and weak-strong uniqueness for the nonhomogeneous Navier-Stokes system. J. Anal. Math. 105(2008), 169–196. http://dx.doi.org/10.1007/s11854-008-0034-4 Google Scholar
[7] Grafakos, L., Classical and modern Fourier analysis. Pearson Education, Inc., Upper Saddle River, NJ, 2004.Google Scholar
[8] Hörmander, L., Pseudo-differential operators and hypoelliptic equations. Singular integrals (Proc. Sympos. Pure Math., Vol. X, Chicago, Ill., 1966), American Mathematical Society, Providence, RI, 1967, pp. 138–183.Google Scholar
[9] Kurtz, D. S. and Wheeden, R., Results on weighted norm inequalities for multipliers. Trans. Amer. Math. Soc. 255(1979), 343–362. http://dx.doi.org/10.1090/S0002-9947-1979-0542885-8 Google Scholar
[10] Miller, N., Weighted Sobolev spaces and pseudodifferential operators with smooth symbols. Trans. Amer.Math. Soc. 269(1982), no. 1, 91–109. http://dx.doi.org/10.1090/S0002-9947-1982-0637030-4 Google Scholar
[11] Stein, E. M., Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals. Princeton Mathematical Series, 43, Princeton University Press, Princeton, NJ, 1993.Google Scholar
[12] Stein, E. M. and Weiss, G., Interpolation of operators with change of measures. Trans. Amer. Math. Soc. 87(1958), 159–172. http://dx.doi.org/10.1090/S0002-9947-1958-0092943-6 Google Scholar
[13] Stein, E. M. and Weiss, G., Introduction to Fourier analysis on Euclidean spaces. Princeton Mathematical Series, 32, Princeton University Press, Princeton, NJ, 1971.Google Scholar
[14] Stroffolini, B., Elliptic systems of PDE with BMO-coefficients. Potential Anal. 15(2001), no. 3, 285–299. http://dx.doi.org/10.1023/A:1011290420956 Google Scholar