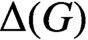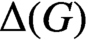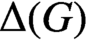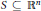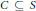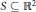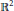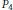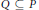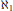3 results
THE CHARACTER GRAPH OF A FINITE GROUP IS PERFECT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 18 November 2020, pp. 127-131
- Print publication:
- August 2021
-
- Article
- Export citation
2-dimensional Convexity Numbers and P4-free Graphs
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 1 / 14 March 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 61-71
- Print publication:
- 14 March 2014
-
- Article
-
- You have access
- Export citation
A Note on Conjectures of F. Galvin and R. Rado
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 317-325
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation