Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T20:16:03.013Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Conjectures of F. Galvin and R. Rado

Published online by Cambridge University Press:  20 November 2018

François G. Dorais
François G. Dorais*
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1968, Galvin conjectured that an uncountable poset $P$ is the union of countably many chains if and only if this is true for every subposet 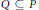$Q\,\subseteq \,P$ with size 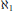${{\aleph }_{1}}$. In 1981, Rado formulated a similar conjecture that an uncountable interval graph $G$ is countably chromatic if and only if this is true for every induced subgraph 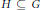$H\,\subseteq \,G$ with size 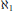${{\aleph }_{1}}$. Todorčević has shown that Rado's conjecture is consistent relative to the existence of a supercompact cardinal, while the consistency of Galvin's conjecture remains open. In this paper, we survey and collect a variety of results related to these two conjectures. We also show that the extension of Rado's conjecture to the class of all chordal graphs is relatively consistent with the existence of a supercompact cardinal.

Keywords

03E0503E3503E55Galvin conjectureRado conjectureperfect graphcomparability graphchordal graphclique-cover numberchromatic number
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 2 , 01 June 2013 , pp. 317 - 325
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Abraham, U., A note on Dilworth's theorem in the infinite case. Order 4(1987), no. 2, 107–125. http://dx.doi.org/10.1007/BF00337691 Google Scholar
[2] Berge, C., Les probl`emes de coloration en théorie des graphes. Publ. Inst. Statist. Univ. Paris 9(1960), 123–160.Google Scholar
[3] Chudnovsky, M., Robertson, N., Seymour, P., and Thomas, R., The strong perfect graph theorem. Ann. of Math. (2) 164(2006), no. 1, 51–229. http://dx.doi.org/10.4007/annals.2006.164.51Google Scholar
[4] Dilworth, R. P., A decomposition theorem for partially ordered sets. Ann. of Math. (2) 51(1950), 161–166. http://dx.doi.org/10.2307/1969503 Google Scholar
[5] Fulkerson, D. R. and Gross, O. A., Incidence matrices and interval graphs. Pacific J. Math. 15(1965), 835–855.Google Scholar
[6] Hajnal, A. and Surańyi, J., über die Auflösung von Graphen in vollstandige Teilgraphen, Ann. Univ. Sci. Budapest. Eotvos Sect. Math. 1(1958), 113–121.Google Scholar
[7] König, B., Generic compactness reformulated. Arch. Math. Logic 43(2004), no. 3, 311–326. http://dx.doi.org/10.1007/s00153-003-0211-1 Google Scholar
[8] Lovász, L., Normal hypergraphs and the perfect graph conjecture. Discrete Math. 2(1972), no. 3, 253–267. http://dx.doi.org/10.1016/0012-365X(72)90006-4 Google Scholar
[9] Lovász, L., A characterization of perfect graphs. J. Combinatorial Theory Ser. B 13(1972), 95–98. http://dx.doi.org/10.1016/0095-8956(72)90045-7Google Scholar
[10] Perles, M. A., On Dilworth's theorem in the infinite case. Israel J. Math. 1(1963), 108–109. http://dx.doi.org/10.1007/BF02759806 Google Scholar
[11] Pnueli, A., Lempel, A., and Even, S., Transitive orientation of graphs and identification of permutation graphs. Canad. J. Math. 23(1971), 160–175. http://dx.doi.org/10.4153/CJM-1971-016-5 Google Scholar
[12] Rado, R., Theorems on intervals of ordered sets. Discrete Math. 35(1981), 199–201. http://dx.doi.org/10.1016/0012-365X(81)90208-9 Google Scholar
[13] Todorčević, S., On a conjecture of R. Rado. J. London Math. Soc. (2) 27(1983), no. 1, 1–8. http://dx.doi.org/10.1112/jlms/s2-27.1.1 Google Scholar
[14] Todorčević, S., Conjectures of Rado and Chang and cardinal arithmetic. In: Finite and infinite combinatorics in sets and logic (Banff, AB, 1991), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 411, Kluwer Acad. Publ., Dordrecht, 1993, pp. 385–398.Google Scholar
[15] Todorčević, S., Combinatorial dichotomies in set theory, Bull. Symbolic Logic, 17(2011), no. 1, 1–72. http://dx.doi.org/10.2178/bsl/1294186662 Google Scholar
[16] Trotter, W. T. Jr., Moore, J. I. Jr., and Sumner, D. P., The dimension of a comparability graph. Proc. Amer. Math. Soc. 60(1976), 35–38. http://dx.doi.org/10.1090/S0002-9939-1976-0417001-6 Google Scholar
[17] Wagon, S., Infinite triangulated graphs. Discrete Math. 22(1978), no. 2, 183–189. http://dx.doi.org/10.1016/0012-365X(78)90123-1 Google Scholar