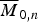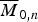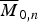1 results
Modular Interpretation of a Non-Reductive Chow Quotient
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 27 February 2018, pp. 457-477
-
- Article
-
- You have access
- Export citation
-
The space of n distinct points and adisjoint parametrized hyperplane in projective d-space up to projectivity – equivalently, configurations of n distinct points in affine d-space up to translation and homothety – has a beautiful compactification introduced by Chen, Gibney and Krashen. This variety, constructed inductively using the apparatus of Fulton–MacPherson configuration spaces, is a parameter space of certain pointed rational varieties whose dual intersection complex is a rooted tree. This generalizes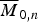
$\overline M _{0,n}$ and shares many properties with it. In this paper, we prove that the normalization of the Chow quotient of (ℙd)n by the diagonal action of the subgroup of projectivities fixing a hyperplane, pointwise, is isomorphic to this Chen–Gibney–Krashen space Td, n. This is a non-reductive analogue of Kapranov's famous quotient construction of 
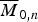$\overline M _{0,n}$, and indeed as a special case we show that 
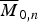$\overline M _{0,n}$ is the Chow quotient of (ℙ1)n−1 by an action of 𝔾m ⋊ 𝔾a.
