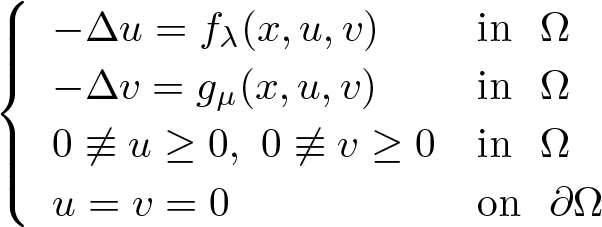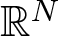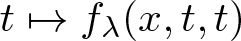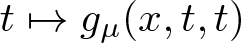In this work, we are interested in studying the following class of problems:(𝒫λμ)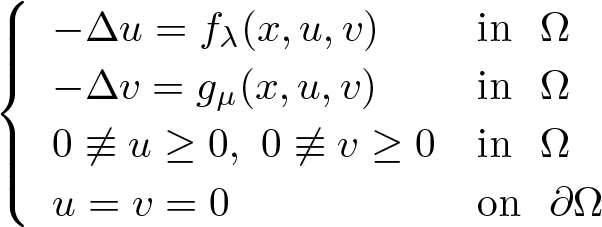 \begin{align}\left\{\begin{array}{ll}-\Delta u=f_\lambda(x,u,v)& \text{in}~~\Omega\\-\Delta v=g_\mu(x,u,v) & \text{in}~~\Omega\\0\not\equiv u\geq 0,\,\,0\not\equiv v\geq 0& \text{in}~~\Omega\\u=v=0&\text{on}~~\partial\Omega\end{array}\right.\end{align}
\begin{align}\left\{\begin{array}{ll}-\Delta u=f_\lambda(x,u,v)& \text{in}~~\Omega\\-\Delta v=g_\mu(x,u,v) & \text{in}~~\Omega\\0\not\equiv u\geq 0,\,\,0\not\equiv v\geq 0& \text{in}~~\Omega\\u=v=0&\text{on}~~\partial\Omega\end{array}\right.\end{align}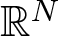 $\mathbb{R}^N$, λ > 0, µ > 0,
$\mathbb{R}^N$, λ > 0, µ > 0, 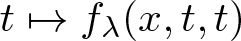 $t\mapsto f_\lambda(x,t,t)$ and
$t\mapsto f_\lambda(x,t,t)$ and 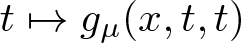 $t\mapsto g_\mu(x,t,t)$ have concave-convex type nonlinearities. We present results related to the existence and non-existence of solutions for problem
$t\mapsto g_\mu(x,t,t)$ have concave-convex type nonlinearities. We present results related to the existence and non-existence of solutions for problem  $(\mathcal{P}_{\lambda\mu})$.
$(\mathcal{P}_{\lambda\mu})$.