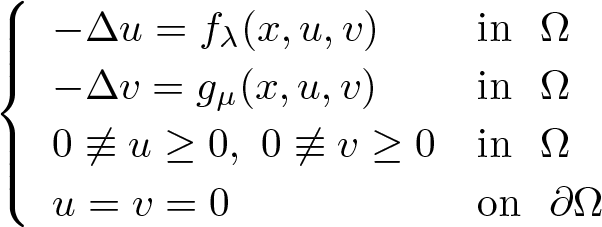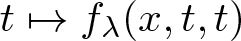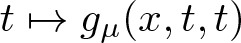1. Introduction
To contextualize our work, we will begin by discussing the scalar case (a single equation), which serves as motivation for the system addressed in our research. Let us consider the following problem:
 \begin{align}
\left\{
\begin{array}{ll}
-\Delta u=\lambda a(x)u^q+b(x)u^p& \text{in}~~\Omega\\
u=0&\text{on}~~\partial\Omega.
\end{array}
\right.
\end{align}
\begin{align}
\left\{
\begin{array}{ll}
-\Delta u=\lambda a(x)u^q+b(x)u^p& \text{in}~~\Omega\\
u=0&\text{on}~~\partial\Omega.
\end{array}
\right.
\end{align} Here, ![]() $\Omega \subset \mathbb{R}^N$ is a bounded domain,
$\Omega \subset \mathbb{R}^N$ is a bounded domain, ![]() $a, b \in L^\infty(\Omega)$, λ > 0 and
$a, b \in L^\infty(\Omega)$, λ > 0 and ![]() $0 \lt q \lt 1 \lt p$. When
$0 \lt q \lt 1 \lt p$. When ![]() $a \equiv b \equiv 1$, Ambrosetti, Brézis and Cerami in [Reference Ambrosetti, Brézis and Cerami4] studied this problem. The authors showed that there exists
$a \equiv b \equiv 1$, Ambrosetti, Brézis and Cerami in [Reference Ambrosetti, Brézis and Cerami4] studied this problem. The authors showed that there exists ![]() $\Lambda \gt 0$ such that
$\Lambda \gt 0$ such that ![]() $(\mathcal{P}_\lambda)$ has a positive solution when
$(\mathcal{P}_\lambda)$ has a positive solution when ![]() $0 \lt \lambda \leq \Lambda$, and there is no positive solution when
$0 \lt \lambda \leq \Lambda$, and there is no positive solution when ![]() $\lambda \gt \Lambda$. Moreover, if
$\lambda \gt \Lambda$. Moreover, if ![]() $p + 1 \leq 2^* := 2N/(N - 2)$, then the solutions of
$p + 1 \leq 2^* := 2N/(N - 2)$, then the solutions of ![]() $(\mathcal{P}_\lambda)$ correspond to critical points of the functional
$(\mathcal{P}_\lambda)$ correspond to critical points of the functional ![]() $I_\lambda \in C^1(H_0^1(\Omega), \mathbb{R})$ defined by
$I_\lambda \in C^1(H_0^1(\Omega), \mathbb{R})$ defined by
 \begin{equation*}
I_\lambda(u) = \int_\Omega |\nabla u|^2 - \frac{\lambda}{q + 1} \int_\Omega |u|^{q + 1} - \frac{1}{p + 1} \int_\Omega |u|^{p + 1}.
\end{equation*}
\begin{equation*}
I_\lambda(u) = \int_\Omega |\nabla u|^2 - \frac{\lambda}{q + 1} \int_\Omega |u|^{q + 1} - \frac{1}{p + 1} \int_\Omega |u|^{p + 1}.
\end{equation*} Using variational methods and techniques introduced by Brézis and Nirenberg in [Reference Brézis and Nirenberg12], they showed the existence of a second positive solution for ![]() $0 \lt \lambda \lt \Lambda$ (it is necessary to demand some regularity for the domain in order to guarantee the existence of the unit exterior normal vector to
$0 \lt \lambda \lt \Lambda$ (it is necessary to demand some regularity for the domain in order to guarantee the existence of the unit exterior normal vector to ![]() $\partial\Omega$. See, for example, [Reference Ambrosetti, Brézis and Cerami4, Lemma 4.1]). From a purely mathematical perspective, problems with concave-convex type nonlinearities have received great interest since the seminal work [Reference Ambrosetti, Brézis and Cerami4]. The list of references is extensive, among which we highlight [Reference Barrios, Colorado, De Pablo and Sánchez6–Reference Bartsch and Willem8, Reference Brändle, Colorado, De Pablo and Sánchez10, Reference García-Azorero and Peral28–Reference García-Azorero, Peral and Rossi30, Reference Hirano, Saccon and Shioji34, Reference Marano and Papageorgiou39, Reference Tang44, Reference Wang45, Reference Wu47]. Recently, there has been considerable interest in problems with indefinite weights, that is, problems where the weight functions
$\partial\Omega$. See, for example, [Reference Ambrosetti, Brézis and Cerami4, Lemma 4.1]). From a purely mathematical perspective, problems with concave-convex type nonlinearities have received great interest since the seminal work [Reference Ambrosetti, Brézis and Cerami4]. The list of references is extensive, among which we highlight [Reference Barrios, Colorado, De Pablo and Sánchez6–Reference Bartsch and Willem8, Reference Brändle, Colorado, De Pablo and Sánchez10, Reference García-Azorero and Peral28–Reference García-Azorero, Peral and Rossi30, Reference Hirano, Saccon and Shioji34, Reference Marano and Papageorgiou39, Reference Tang44, Reference Wang45, Reference Wu47]. Recently, there has been considerable interest in problems with indefinite weights, that is, problems where the weight functions ![]() $a(\cdot)$ or
$a(\cdot)$ or ![]() $b(\cdot)$ may change sign. De Figueiredo, Gossez and Ubilla in the work [Reference De Figueiredo, Gossez and Ubilla25, Corollary 2.2 and Corollary 2.7] showed existence and non-existence results for
$b(\cdot)$ may change sign. De Figueiredo, Gossez and Ubilla in the work [Reference De Figueiredo, Gossez and Ubilla25, Corollary 2.2 and Corollary 2.7] showed existence and non-existence results for ![]() $(\mathcal{P}_\lambda)$ when
$(\mathcal{P}_\lambda)$ when ![]() $a(\cdot)$ and
$a(\cdot)$ and ![]() $b(\cdot)$ satisfy certain conditions, including the possibility of
$b(\cdot)$ satisfy certain conditions, including the possibility of ![]() $a(\cdot)$ and
$a(\cdot)$ and ![]() $b(\cdot)$ changing sign. More specifically, they showed that there exists
$b(\cdot)$ changing sign. More specifically, they showed that there exists ![]() $\lambda_0 \gt 0$ and
$\lambda_0 \gt 0$ and ![]() $\overline{c} \gt 0$ such that
$\overline{c} \gt 0$ such that ![]() $(\mathcal{P}_\lambda)$ admits two solutions when
$(\mathcal{P}_\lambda)$ admits two solutions when ![]() $p\leq 2^*-1$ and
$p\leq 2^*-1$ and ![]() $0 \lt \lambda \lt \lambda_0$ and admits no solution if
$0 \lt \lambda \lt \lambda_0$ and admits no solution if ![]() $p\leq 2^*-1$ and
$p\leq 2^*-1$ and ![]() $\lambda \gt \overline{c}$. In a later work [Reference De Figueiredo, Gossez and Ubilla26, Theorem 4.1 and Theorem 4.2], assuming certain conditions, including:
$\lambda \gt \overline{c}$. In a later work [Reference De Figueiredo, Gossez and Ubilla26, Theorem 4.1 and Theorem 4.2], assuming certain conditions, including: ![]() $a,\,b\in L^\infty(\Omega)$,
$a,\,b\in L^\infty(\Omega)$, ![]() $0\not\equiv a(x)\geq 0$ in Ω, and
$0\not\equiv a(x)\geq 0$ in Ω, and ![]() $\inf_{B_1}a(x) \gt 0$ for some ball
$\inf_{B_1}a(x) \gt 0$ for some ball ![]() $B_1\subset\Omega$, the same authors recovered the results obtained by Ambrosetti et al. [Reference Ambrosetti, Brézis and Cerami4], that is, they showed that there exists
$B_1\subset\Omega$, the same authors recovered the results obtained by Ambrosetti et al. [Reference Ambrosetti, Brézis and Cerami4], that is, they showed that there exists ![]() $0 \lt \Lambda\leq\infty$ such that: If
$0 \lt \Lambda\leq\infty$ such that: If ![]() $0\leq q \lt 1 \lt p$, the problem
$0\leq q \lt 1 \lt p$, the problem ![]() $(\mathcal{P}_\lambda)$ has at least one solution when
$(\mathcal{P}_\lambda)$ has at least one solution when ![]() $0 \lt \lambda\leq\Lambda$ and admits no solution when
$0 \lt \lambda\leq\Lambda$ and admits no solution when ![]() $\lambda \gt \Lambda\neq+\infty$. If
$\lambda \gt \Lambda\neq+\infty$. If ![]() $0\leq q \lt 1 \lt p\leq 2^*-1$, the problem
$0\leq q \lt 1 \lt p\leq 2^*-1$, the problem ![]() $(\mathcal{P}_\lambda)$ admits at least two solutions when
$(\mathcal{P}_\lambda)$ admits at least two solutions when ![]() $0 \lt \lambda \lt \Lambda$.
$0 \lt \lambda \lt \Lambda$.
The results provided by the works [Reference Ambrosetti, Brézis and Cerami4, Reference De Figueiredo, Gossez and Ubilla26] include nonlinearities with supercritical growth. In the context of the Laplacian operator, when Ω is bounded, the problem ![]() $-\Delta u=f(x,u)$ in Ω and u = 0 on
$-\Delta u=f(x,u)$ in Ω and u = 0 on ![]() $\partial\Omega$, is said to have supercritical growth when there is no C > 0 such that
$\partial\Omega$, is said to have supercritical growth when there is no C > 0 such that  $|f(x,t)|\leq C(1+|t|^{2^{\ast}-1})$, a.e.
$|f(x,t)|\leq C(1+|t|^{2^{\ast}-1})$, a.e. ![]() $x\in\Omega$ and
$x\in\Omega$ and ![]() $t\in\mathbb{R}$, where
$t\in\mathbb{R}$, where ![]() $2^*=2N/(N-2)$ is the critical exponent of the Sobolev Embedding and
$2^*=2N/(N-2)$ is the critical exponent of the Sobolev Embedding and ![]() $N\geq 3$. In this sense, the problem
$N\geq 3$. In this sense, the problem ![]() $(\mathcal{P}_\lambda)$ has supercritical growth when
$(\mathcal{P}_\lambda)$ has supercritical growth when ![]() $p \gt 2^*-1$ and
$p \gt 2^*-1$ and ![]() $N\geq 3$.
$N\geq 3$.
The literature concerning problems with concave-convex type nonlinearities, as can be seen in the works we mentioned earlier, is rich in problems whose nonlinearity can have supercritical growth. For problems with supercritical growth and nonlinearities that are not concave-convex type, see for example [Reference Albalawi, Mercuri and Moroz3, Reference Arcoya, Boccardo and Orsina5, Reference Candela, Palmieri and Salvatore15, Reference Candela, Perera and Sportelli16, Reference Clapp and Tiwari21]. To the best of our knowledge, very few existence results have been determined for elliptic systems with supercritical growth (see [Reference Candela and Sportelli17, Reference Da Silva22]).
Consider the following system:
Although there is a substantial literature related to scalar problems involving concave-convex type nonlinearities, to this day the results of Ambrosetti et al. [Reference Ambrosetti, Brézis and Cerami4] have not been fully recovered for systems of type (1.1) in which:
 \begin{equation}
\left\{
\begin{array}{lcl}
f_\lambda(x,t,t)=\lambda a(x)t^{q_1}+c(x)t^{p_1}\,\,\mbox{and}\,\,g_\mu(x,t,t)=\mu b(x)t^{q_2}+d(x)t^{p_2}\\
a,b,c,d\in L^\infty(\Omega),\,\,0\leq q_i \lt 1 \lt p_i.
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{lcl}
f_\lambda(x,t,t)=\lambda a(x)t^{q_1}+c(x)t^{p_1}\,\,\mbox{and}\,\,g_\mu(x,t,t)=\mu b(x)t^{q_2}+d(x)t^{p_2}\\
a,b,c,d\in L^\infty(\Omega),\,\,0\leq q_i \lt 1 \lt p_i.
\end{array}
\right.
\end{equation} To date, issues such as non-existence of solution, as well as the existence of solutions for systems with nonlinearities exhibiting supercritical growth (i.e. ![]() $p_i \gt 2^*-1$ in Equation (1.2)), have not been addressed in the current literature. In general, research involving Equations (1.1)–(1.2) as well as its generalizations is almost entirely restricted to gradient-type systems, a concept we will explain next. Consider the following system:
$p_i \gt 2^*-1$ in Equation (1.2)), have not been addressed in the current literature. In general, research involving Equations (1.1)–(1.2) as well as its generalizations is almost entirely restricted to gradient-type systems, a concept we will explain next. Consider the following system:
 \begin{equation}
\left\{
\begin{array}{ll}
-\mathcal{L}_i u=\phi_i(x,u_1,u_2)& \mbox{in}~~\Omega \subset\mathbb{R}^N,\,\,i=1,2
\\
u_i=0&\mbox{on}~~\partial\Omega,
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{ll}
-\mathcal{L}_i u=\phi_i(x,u_1,u_2)& \mbox{in}~~\Omega \subset\mathbb{R}^N,\,\,i=1,2
\\
u_i=0&\mbox{on}~~\partial\Omega,
\end{array}
\right.
\end{equation} it will be called a gradient-type system if there exists ![]() $G(x,\cdot,\cdot)\in C^1(\mathbb{R}^2)$ a.e. in Ω, such that
$G(x,\cdot,\cdot)\in C^1(\mathbb{R}^2)$ a.e. in Ω, such that ![]() $\phi_i(x,t_1,t_2)=G_{t_i}(x,t_1,t_2)$. The importance of this type of system lies in the fact that it is possible to associate to them an Euler–Lagrange functional.
$\phi_i(x,t_1,t_2)=G_{t_i}(x,t_1,t_2)$. The importance of this type of system lies in the fact that it is possible to associate to them an Euler–Lagrange functional.
As far as we know, Wu in [Reference Wu46] was the first author to consider a system with nonlinearities of type (1.2) and Dirichlet boundary condition. The author studied the following gradient-type system: Equation (1.3) with ![]() $\mathcal{L}_i=\Delta$ and
$\mathcal{L}_i=\Delta$ and ![]() $\phi_i(x,u_1,u_2)=G_{u_i}(x,u_1,v_2)$ where
$\phi_i(x,u_1,u_2)=G_{u_i}(x,u_1,v_2)$ where
 \begin{equation*}
G(x,u_1,u_2)=\dfrac{\lambda a(x)}{q+1}|u_1|^{q+1}+\dfrac{\mu b(x)}{q+1}|u_2|^{q+1}
+\dfrac{c(x)}{\alpha+\beta}|u_1|^\alpha|u_2|^\beta.
\end{equation*}
\begin{equation*}
G(x,u_1,u_2)=\dfrac{\lambda a(x)}{q+1}|u_1|^{q+1}+\dfrac{\mu b(x)}{q+1}|u_2|^{q+1}
+\dfrac{c(x)}{\alpha+\beta}|u_1|^\alpha|u_2|^\beta.
\end{equation*} When ![]() $0 \lt q \lt 1$,
$0 \lt q \lt 1$, ![]() $2 \lt \alpha+\beta \lt 2^*$,
$2 \lt \alpha+\beta \lt 2^*$, ![]() $a^+(x):=\max\{a(x),0\}\not\equiv 0$,
$a^+(x):=\max\{a(x),0\}\not\equiv 0$, ![]() $b^+(x):=\max\{b(x),0\}\not\equiv 0$, and
$b^+(x):=\max\{b(x),0\}\not\equiv 0$, and ![]() $c\in C^0(\overline{\Omega})$ with
$c\in C^0(\overline{\Omega})$ with ![]() $0\not\equiv c(x)\geq 0$ in Ω, using variational methods and assuming certain conditions on the weight functions, the author provided results on existence and multiplicity of non-negative solutions, provided that λ > 0 and µ > 0 are sufficiently small.
$0\not\equiv c(x)\geq 0$ in Ω, using variational methods and assuming certain conditions on the weight functions, the author provided results on existence and multiplicity of non-negative solutions, provided that λ > 0 and µ > 0 are sufficiently small.
There are many works dealing with the existence or multiplicity of non-negative solutions for systems with concave-convex nonlinearities of type (1.2), or even for systems involving the p-Laplacian operator and nonlinearities that generalize Equation (1.2). However, the approach we encounter in these works, in general, is the same as that used to address the problem ![]() $(\mathcal{P}_\lambda)$ from a variational perspective, so they are restricted to cases where the system is of gradient type and the nonlinearities exhibit subcritical or critical growth, i.e.
$(\mathcal{P}_\lambda)$ from a variational perspective, so they are restricted to cases where the system is of gradient type and the nonlinearities exhibit subcritical or critical growth, i.e. ![]() $p_i\leq 2^*$ in Equation (1.2). Furthermore, the results are limited to local cases, in the sense that the existence of a solution is guaranteed only if the parameters λ > 0 and µ > 0 in Equation (1.1) are sufficiently small. The same applies to systems that generalize Equation (1.1) to more general operators. Regarding gradient-type systems (1.2)–(1.1), as well as their generalizations involving the operators: p-Laplacian (in this case
$p_i\leq 2^*$ in Equation (1.2). Furthermore, the results are limited to local cases, in the sense that the existence of a solution is guaranteed only if the parameters λ > 0 and µ > 0 in Equation (1.1) are sufficiently small. The same applies to systems that generalize Equation (1.1) to more general operators. Regarding gradient-type systems (1.2)–(1.1), as well as their generalizations involving the operators: p-Laplacian (in this case ![]() $0\leq q_i \lt p-1 \lt p_i$), fractional Laplacian and p&q-Laplacian, we refer to the following works and the references contained therein [Reference Afrouzi and Rasouli2, 3.2, Reference Batkam and Colin9, Reference Chen and Deng18, Reference Cheng, Feng and Wei19, Reference He, Squassina and Zou32, Reference Li and Yang38, Reference Song, Chen and Yan42, Reference Yin48] (see also [Reference Brown and Wu14, Reference Rasouli and Afrouzi41] for nonlinearities on
$0\leq q_i \lt p-1 \lt p_i$), fractional Laplacian and p&q-Laplacian, we refer to the following works and the references contained therein [Reference Afrouzi and Rasouli2, 3.2, Reference Batkam and Colin9, Reference Chen and Deng18, Reference Cheng, Feng and Wei19, Reference He, Squassina and Zou32, Reference Li and Yang38, Reference Song, Chen and Yan42, Reference Yin48] (see also [Reference Brown and Wu14, Reference Rasouli and Afrouzi41] for nonlinearities on ![]() $\partial\Omega$).
$\partial\Omega$).
As mentioned earlier, the current literature involving Equations (1.1)–(1.2) and their generalizations is almost entirely restricted to gradient-type systems. This implies that the exponent pi appearing in Equation (1.2) is bounded by a power associated with the space in which the Euler–Lagrange functional is well-defined.
Some works involving systems require additional comments. In [Reference Da Silva22], the author of the present work studied the system (1.1)–(1.2) with:
 \begin{equation}
\left\{
\begin{array}{lcl}
f_\lambda(x,u,v)&=&\lambda a(x)u^{q_1}-\tau c(x)u^{\alpha-1}v^\beta
\\
g_\mu(x,u,v)&=&\mu b(x)v^{q_2}-\delta d(x)u^\alpha v^{\beta-1},
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{lcl}
f_\lambda(x,u,v)&=&\lambda a(x)u^{q_1}-\tau c(x)u^{\alpha-1}v^\beta
\\
g_\mu(x,u,v)&=&\mu b(x)v^{q_2}-\delta d(x)u^\alpha v^{\beta-1},
\end{array}
\right.
\end{equation} where ![]() $\lambda,\mu,\delta,\tau \gt 0$,
$\lambda,\mu,\delta,\tau \gt 0$, ![]() $0 \lt q_i \lt 1$,
$0 \lt q_i \lt 1$, ![]() $a^+(\cdot)\not\equiv0$,
$a^+(\cdot)\not\equiv0$, ![]() $b^+(\cdot)\not\equiv0$ in Ω and
$b^+(\cdot)\not\equiv0$ in Ω and ![]() $c(x)\equiv d(x)\geq 0$ in Ω. In said work, we showed the existence of a solution (u, v) such that
$c(x)\equiv d(x)\geq 0$ in Ω. In said work, we showed the existence of a solution (u, v) such that ![]() $0\not\equiv u\geq 0$ and
$0\not\equiv u\geq 0$ and ![]() $0\not\equiv v\geq 0$ in Ω, provided that
$0\not\equiv v\geq 0$ in Ω, provided that ![]() $\alpha,\beta\geq 1$ and
$\alpha,\beta\geq 1$ and ![]() $\alpha+\beta \gt 2$ (in this case
$\alpha+\beta \gt 2$ (in this case ![]() $p_i=\alpha+\beta-1 \lt +\infty$). This system, although only of gradient type for specific values of τ > 0 and δ > 0, can be converted into a gradient-type system for all
$p_i=\alpha+\beta-1 \lt +\infty$). This system, although only of gradient type for specific values of τ > 0 and δ > 0, can be converted into a gradient-type system for all ![]() $\tau,\delta \gt 0$ (see [Reference Da Silva22,
Proof of Theorem 1.1 ]). However, the approach of this work cannot be applied to systems that do not have the specific form (1.4) or for cases where
$\tau,\delta \gt 0$ (see [Reference Da Silva22,
Proof of Theorem 1.1 ]). However, the approach of this work cannot be applied to systems that do not have the specific form (1.4) or for cases where ![]() $c(\cdot)$ or
$c(\cdot)$ or ![]() $d(\cdot)$ in Equation (1.2) may change sign, or for cases where
$d(\cdot)$ in Equation (1.2) may change sign, or for cases where ![]() $c(\cdot)\not\equiv d(\cdot)$ in Ω.
$c(\cdot)\not\equiv d(\cdot)$ in Ω.
The only work we are aware of that deals with a class of systems that are not of gradient type is [Reference Chhetri, Raynor and Robinson20]; in this work, Chhetri et al. showed the existence of a solution (u, v) for Equation (1.1) such that u and v are positive in Ω, without necessarily requiring the system to be of gradient type. However, fλ and gµ, by assumption, must have subcritical growth (see [Reference Chhetri, Raynor and Robinson20, Theorem 2.8 and Condition (H1)]). The conditions on fλ and gµ are more restrictive than those addressed in the present paper; for instance, it is required that there exists ![]() $R_0 \gt 0$ such that
$R_0 \gt 0$ such that ![]() $f_\lambda(x,t,s) \gt \lambda_1(\Omega)s+1$ for every
$f_\lambda(x,t,s) \gt \lambda_1(\Omega)s+1$ for every ![]() $t\geq0$ and
$t\geq0$ and ![]() $s \gt R_0$, and
$s \gt R_0$, and ![]() $g_\mu(x,t,s) \gt \lambda_1(\Omega)t+1$ for every
$g_\mu(x,t,s) \gt \lambda_1(\Omega)t+1$ for every ![]() $s\geq0$ and
$s\geq0$ and ![]() $t \gt R_0$ (see [Reference Chhetri, Raynor and Robinson20, p. 43]), where
$t \gt R_0$ (see [Reference Chhetri, Raynor and Robinson20, p. 43]), where ![]() $\lambda_1(\Omega)$ is the first eigenvalue of
$\lambda_1(\Omega)$ is the first eigenvalue of ![]() $(-\Delta, H_0^1(\Omega))$. In the present work, fλ and gµ do not necessarily need to satisfy the latter condition nor Condition (H1) from [Reference Chhetri, Raynor and Robinson20]; the class of nonlinearities addressed in this paper is more general and allows for nonlinearities with supercritical growth.
$(-\Delta, H_0^1(\Omega))$. In the present work, fλ and gµ do not necessarily need to satisfy the latter condition nor Condition (H1) from [Reference Chhetri, Raynor and Robinson20]; the class of nonlinearities addressed in this paper is more general and allows for nonlinearities with supercritical growth.
Candela and Sportelli in [Reference Candela and Sportelli17] considered the following system:
 \begin{equation}
\begin{cases}
-\text{div}(a(x, u, \nabla u)) + A_t(x, u, \nabla u) = G_u(x, u, v) & \text{in } \Omega, \\
-\text{div}(b(x, v, \nabla v)) + B_t(x, v, \nabla v) = G_v (x, u, v) & \text{in } \Omega, \\
u = v = 0 & \text{on } \partial\Omega,
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
-\text{div}(a(x, u, \nabla u)) + A_t(x, u, \nabla u) = G_u(x, u, v) & \text{in } \Omega, \\
-\text{div}(b(x, v, \nabla v)) + B_t(x, v, \nabla v) = G_v (x, u, v) & \text{in } \Omega, \\
u = v = 0 & \text{on } \partial\Omega,
\end{cases}
\end{equation} where ![]() $a(x,t,\xi)=(\partial_{\xi_1}A,\ldots,\partial_{\xi_N}A)$ and
$a(x,t,\xi)=(\partial_{\xi_1}A,\ldots,\partial_{\xi_N}A)$ and ![]() $b(x,t,\xi)=(\partial_{\xi_1}B,\ldots,\partial_{\xi_N}B)$, and the Euler–Lagrange functional associated with this system is defined on the Banach space
$b(x,t,\xi)=(\partial_{\xi_1}B,\ldots,\partial_{\xi_N}B)$, and the Euler–Lagrange functional associated with this system is defined on the Banach space  $X:=(W^{1,p_1}_0(\Omega)\cap L^\infty(\Omega))\times(W^{1,p_2}_0(\Omega)\cap L^\infty(\Omega))$ (see [Reference Candela and Sportelli17, (1.6)]). Assuming certain conditions (see [Reference Candela and Sportelli17,
$X:=(W^{1,p_1}_0(\Omega)\cap L^\infty(\Omega))\times(W^{1,p_2}_0(\Omega)\cap L^\infty(\Omega))$ (see [Reference Candela and Sportelli17, (1.6)]). Assuming certain conditions (see [Reference Candela and Sportelli17, ![]() $(h_0)-(h_7)$ and
$(h_0)-(h_7)$ and ![]() $(g_0)-(g_4)$]), among which
$(g_0)-(g_4)$]), among which ![]() $A(x,t,\xi)$ and
$A(x,t,\xi)$ and ![]() $B(x,t,\xi)$ grow at least as fast as
$B(x,t,\xi)$ grow at least as fast as ![]() $(1 + |t|^{s_{1}p_{1}})|\xi|^{p_{1}}$ and
$(1 + |t|^{s_{1}p_{1}})|\xi|^{p_{1}}$ and ![]() $(1 + |t|^{s_{2}p_{2}})|\xi|^{p_{2}}$ respectively, where
$(1 + |t|^{s_{2}p_{2}})|\xi|^{p_{2}}$ respectively, where ![]() $p_i \gt 1$,
$p_i \gt 1$, ![]() $s_i\geq 0$, the authors showed that if
$s_i\geq 0$, the authors showed that if
 \begin{equation}
\limsup_{(u,v) \rightarrow (0,0)} \dfrac{G(x, u, v)}{|u|^{p_1} + |v|^{p_2}} \lt \alpha_2 \min\{\lambda_{1,1}, \lambda_{2,1}\} \quad \text{uniformly a.e. in } \Omega,
\end{equation}
\begin{equation}
\limsup_{(u,v) \rightarrow (0,0)} \dfrac{G(x, u, v)}{|u|^{p_1} + |v|^{p_2}} \lt \alpha_2 \min\{\lambda_{1,1}, \lambda_{2,1}\} \quad \text{uniformly a.e. in } \Omega,
\end{equation} where ![]() $\lambda_{i,1}$ is the first eigenvalue of
$\lambda_{i,1}$ is the first eigenvalue of  $(-\Delta_{p_i},W_0^{1,p_i})$ and
$(-\Delta_{p_i},W_0^{1,p_i})$ and ![]() $\alpha_2 \gt 0$ is a constant related to the growth of A and B (see [Reference Candela and Sportelli17, Theorem 4.1]), then Equation (1.5) admits a non-trivial solution (see [Reference Candela and Sportelli17, Theorems 1.1 and 4.1]), assuming additional conditions they showed the existence of infinitely many solutions for Equation (1.5). The notable characteristic of the work of these authors is that they provided an existence result for the system (1.5) with the possibility of
$\alpha_2 \gt 0$ is a constant related to the growth of A and B (see [Reference Candela and Sportelli17, Theorem 4.1]), then Equation (1.5) admits a non-trivial solution (see [Reference Candela and Sportelli17, Theorems 1.1 and 4.1]), assuming additional conditions they showed the existence of infinitely many solutions for Equation (1.5). The notable characteristic of the work of these authors is that they provided an existence result for the system (1.5) with the possibility of ![]() $G(x,u,v)$ having a supercritical growth, in the sense of, the exponents q 1 and q 2 that appear in the growth of Gu and Gv respectively (see [Reference Candela and Sportelli17,
$G(x,u,v)$ having a supercritical growth, in the sense of, the exponents q 1 and q 2 that appear in the growth of Gu and Gv respectively (see [Reference Candela and Sportelli17, ![]() $(g_1)$]), satisfy:
$(g_1)$]), satisfy:
In this case, depending on the choice of si, it is possible to have ![]() $p_i^* \lt q_i \lt p^*_i(s_i+1)$ where
$p_i^* \lt q_i \lt p^*_i(s_i+1)$ where ![]() $p^*_i$ is the critical Sobolev exponent associated with
$p^*_i$ is the critical Sobolev exponent associated with  $W^{1,p_i}_0(\Omega)$; the multiplicity result provided by these authors also allows for supercritical growth for G. However, no information about the sign of the solutions was given. When
$W^{1,p_i}_0(\Omega)$; the multiplicity result provided by these authors also allows for supercritical growth for G. However, no information about the sign of the solutions was given. When ![]() $A=(1/p_1)|\xi|^{p_1}$ and
$A=(1/p_1)|\xi|^{p_1}$ and ![]() $B=(1/p_2)|\xi|^{p_2}$, the system (1.5) becomes
$B=(1/p_2)|\xi|^{p_2}$, the system (1.5) becomes
Thus ![]() $s_1=s_2=0$ and the nonlinearities Gu and Gv only have subcritical growth (see [Reference Candela and Sportelli17, Remark 3.1]). Although the techniques we employ in this work are not only directed at gradient-type systems, our results include nonlinearities that do not satisfy Equation (1.6). For example, if
$s_1=s_2=0$ and the nonlinearities Gu and Gv only have subcritical growth (see [Reference Candela and Sportelli17, Remark 3.1]). Although the techniques we employ in this work are not only directed at gradient-type systems, our results include nonlinearities that do not satisfy Equation (1.6). For example, if ![]() $\gamma_1,\gamma_2 \gt 0$ and
$\gamma_1,\gamma_2 \gt 0$ and ![]() $\gamma_1+\gamma_2 \lt p_i$ (or
$\gamma_1+\gamma_2 \lt p_i$ (or ![]() $\gamma_i \lt p_i$), condition (1.6) prevents G, near the origin, from having nonlinearities that grow like
$\gamma_i \lt p_i$), condition (1.6) prevents G, near the origin, from having nonlinearities that grow like ![]() $|u|^{\gamma_1}|v|^{\gamma_2}$ (or
$|u|^{\gamma_1}|v|^{\gamma_2}$ (or ![]() $|u|^{\gamma_1}+|v|^{\gamma_2}$), which is a common type of nonlinearity in systems that generalize the results of [Reference Ambrosetti, Brézis and Cerami4].
$|u|^{\gamma_1}+|v|^{\gamma_2}$), which is a common type of nonlinearity in systems that generalize the results of [Reference Ambrosetti, Brézis and Cerami4].
The work of Adriouch and El Hamidi [Reference Adriouch and El Hamidi1] arose before [Reference Wu46]. In their work, the authors consider Equation (1.3) as a gradient-type system with subcritical growth, where ![]() $\mathcal{L}_1=-\Delta_{p}$ and
$\mathcal{L}_1=-\Delta_{p}$ and ![]() $\mathcal{L}_2=-\Delta_{q}$. However, the nonlinearity the authors considered is concave-convex only in one of the equations. For example, when
$\mathcal{L}_2=-\Delta_{q}$. However, the nonlinearity the authors considered is concave-convex only in one of the equations. For example, when ![]() $p=q=2$, system (1.3) takes the form (1.1), the exponents of the nonlinearities in Equation (1.2) satisfy
$p=q=2$, system (1.3) takes the form (1.1), the exponents of the nonlinearities in Equation (1.2) satisfy ![]() $0 \lt q_1 \lt 1 \lt p_1=p_2 \lt 2^*$ and
$0 \lt q_1 \lt 1 \lt p_1=p_2 \lt 2^*$ and ![]() $0 \lt q_2=1 \lt p_1=p_2 \lt 2^*$. That is, the second equation has a linear term instead of a concave one.
$0 \lt q_2=1 \lt p_1=p_2 \lt 2^*$. That is, the second equation has a linear term instead of a concave one.
Another fact worth mentioning is that, as in Equation (1.1), in general, the nonlinearity ![]() $\phi_i(x,u,v)$ of Equation (1.3) also depends on a parameter. Typically, we have
$\phi_i(x,u,v)$ of Equation (1.3) also depends on a parameter. Typically, we have ![]() $\phi_1(x,u,v)=\phi_{1,\lambda}(x,u,v)$ and
$\phi_1(x,u,v)=\phi_{1,\lambda}(x,u,v)$ and ![]() $\phi_2(x,u,v)=\phi_{2,\mu}(x,u,v)$. In all the works we are aware of, the authors ensure the existence of a solution only if the parameters λ > 0 and µ > 0 are sufficiently small. In other words, regarding the parameters, there are only local existence results. This raises an important question, for example: when
$\phi_2(x,u,v)=\phi_{2,\mu}(x,u,v)$. In all the works we are aware of, the authors ensure the existence of a solution only if the parameters λ > 0 and µ > 0 are sufficiently small. In other words, regarding the parameters, there are only local existence results. This raises an important question, for example: when ![]() $\phi_1=\phi_{1,\lambda}$ and
$\phi_1=\phi_{1,\lambda}$ and ![]() $\phi_2=\phi_{2,\mu}$ are nonlinearities that generalize Equation (1.2), is the set
$\phi_2=\phi_{2,\mu}$ are nonlinearities that generalize Equation (1.2), is the set ![]() $\mathcal{O}:=\{(\lambda,\mu)\in\mathbb{R}_+^2|$ (1.3) has a solution
$\mathcal{O}:=\{(\lambda,\mu)\in\mathbb{R}_+^2|$ (1.3) has a solution ![]() $(u,v)\,\,\mbox{with}\,\,u,v \gt 0\,\,\mbox{in}\,\Omega\,\}$ bounded or unbounded? We will show in this work that, surprisingly, this set can be unbounded. In relation to the non-existence of a positive solutions for Equations (1.1)–(1.2) (as well as for Equation (1.3) equipped with a condition that generalizes Equation (1.2)), while there is ample literature for the scalar case, there are no studies involving the non-existence issue for systems. None of the previously mentioned works addresses the non-existence of solutions for systems.
$(u,v)\,\,\mbox{with}\,\,u,v \gt 0\,\,\mbox{in}\,\Omega\,\}$ bounded or unbounded? We will show in this work that, surprisingly, this set can be unbounded. In relation to the non-existence of a positive solutions for Equations (1.1)–(1.2) (as well as for Equation (1.3) equipped with a condition that generalizes Equation (1.2)), while there is ample literature for the scalar case, there are no studies involving the non-existence issue for systems. None of the previously mentioned works addresses the non-existence of solutions for systems.
Although our work is inspired by that of Ambrosetti–Brézis–Cerami, our present contribution addresses interesting cases which, to the best of our knowledge, have not been considered before, such as non-gradient type systems. We will also consider nonlinearities with supercritical growth and present novel existence results even for critical and subcritical cases, as well as providing both existence and non-existence results.
In this work, we are dealing with the following systems:
 \begin{equation*}
(\mathcal{P}_1)\,\,\left\{
\begin{array}{ll}
-\Delta u=\lambda a(x)u^q+c(x)u^\alpha v^\beta & \mbox{in}~~\Omega
\\
-\Delta v=\mu b(x)u^p+d(x)u^\theta v^\gamma & \mbox{in}~~\Omega
\\
0\not\equiv u\geq 0,\,\,0\not\equiv v\geq 0& \mbox{in}~~\Omega
\\
u=v=0&\mbox{on}~~\partial\Omega
\end{array}
\right.
\end{equation*}
\begin{equation*}
(\mathcal{P}_1)\,\,\left\{
\begin{array}{ll}
-\Delta u=\lambda a(x)u^q+c(x)u^\alpha v^\beta & \mbox{in}~~\Omega
\\
-\Delta v=\mu b(x)u^p+d(x)u^\theta v^\gamma & \mbox{in}~~\Omega
\\
0\not\equiv u\geq 0,\,\,0\not\equiv v\geq 0& \mbox{in}~~\Omega
\\
u=v=0&\mbox{on}~~\partial\Omega
\end{array}
\right.
\end{equation*}or
 \begin{equation*}
(\mathcal{P}_2)\,\,\left\{
\begin{array}{ll}
-\Delta u=a(x)u^q+\lambda c(x)u^\alpha v^\beta& \mbox{in}~~\Omega
\\
-\Delta v=b(x)v^p+\mu d(x)u^\theta v^\gamma & \mbox{in}~~\Omega
\\
0\not\equiv u\geq 0,\,\,0\not\equiv v\geq 0& \mbox{in}~~\Omega
\\
u=v=0&\mbox{on}~~\partial\Omega
\end{array}
\right.
\end{equation*}
\begin{equation*}
(\mathcal{P}_2)\,\,\left\{
\begin{array}{ll}
-\Delta u=a(x)u^q+\lambda c(x)u^\alpha v^\beta& \mbox{in}~~\Omega
\\
-\Delta v=b(x)v^p+\mu d(x)u^\theta v^\gamma & \mbox{in}~~\Omega
\\
0\not\equiv u\geq 0,\,\,0\not\equiv v\geq 0& \mbox{in}~~\Omega
\\
u=v=0&\mbox{on}~~\partial\Omega
\end{array}
\right.
\end{equation*} where ![]() $p,\,q\in(0,1)$, concerning the exponents, throughout this work, we will always assume that
$p,\,q\in(0,1)$, concerning the exponents, throughout this work, we will always assume that ![]() $\max\{\alpha,\,\beta\} \gt 1$ and
$\max\{\alpha,\,\beta\} \gt 1$ and ![]() $\max\{\theta,\,\gamma\} \gt 1$. More specifically, we have the following hypotheses:
$\max\{\theta,\,\gamma\} \gt 1$. More specifically, we have the following hypotheses:
(PW1)
 $\alpha,\,\gamma\geq1$ and
$\alpha,\,\gamma\geq1$ and  $\beta,\,\theta\, \gt 0$;
$\beta,\,\theta\, \gt 0$;(PW2)
 $0 \lt \alpha \lt 1 \lt \beta$ and
$0 \lt \alpha \lt 1 \lt \beta$ and  $0 \lt \gamma \lt 1 \lt \theta$;
$0 \lt \gamma \lt 1 \lt \theta$;(PW3)
 $\alpha\geq 1,\,\,\beta \gt 0$ and
$\alpha\geq 1,\,\,\beta \gt 0$ and  $0 \lt \gamma \lt 1 \lt \theta$.
$0 \lt \gamma \lt 1 \lt \theta$.
We will comment on the differences between ![]() $(\mathcal{P}_1)$ and
$(\mathcal{P}_1)$ and ![]() $(\mathcal{P}_2)$ by comparing them with their scalar versions. Observe that u is a solution of
$(\mathcal{P}_2)$ by comparing them with their scalar versions. Observe that u is a solution of ![]() $(\mathcal{P}_\lambda)$ if and only if
$(\mathcal{P}_\lambda)$ if and only if  $\overline{u}=\lambda^\frac{-1}{1-q}u$ is a solution to
$\overline{u}=\lambda^\frac{-1}{1-q}u$ is a solution to  $(\mathcal{P}^{\overline{\lambda}})$ where
$(\mathcal{P}^{\overline{\lambda}})$ where  $\overline{\lambda}=\lambda^\frac{p-1}{1-q}$, and
$\overline{\lambda}=\lambda^\frac{p-1}{1-q}$, and
 \begin{align}
\left\{
\begin{array}{ll}
-\Delta u=a(x)u^q+\lambda b(x)u^p& \text{in}~~\Omega
\\
u=v=0&\text{on}~~\partial\Omega.
\end{array}
\right.
\end{align}
\begin{align}
\left\{
\begin{array}{ll}
-\Delta u=a(x)u^q+\lambda b(x)u^p& \text{in}~~\Omega
\\
u=v=0&\text{on}~~\partial\Omega.
\end{array}
\right.
\end{align} When ![]() $a(x)\geq 0$, the global results provided by [Reference De Figueiredo, Gossez and Ubilla26] imply global results for
$a(x)\geq 0$, the global results provided by [Reference De Figueiredo, Gossez and Ubilla26] imply global results for ![]() $(\mathcal{P}^\lambda)$. Here, global means that it is possible to establish for which parameters λ > 0 the problem has a solution and for which it does not, which contrasts with the local case where existence can only be established for small parameters. However, when
$(\mathcal{P}^\lambda)$. Here, global means that it is possible to establish for which parameters λ > 0 the problem has a solution and for which it does not, which contrasts with the local case where existence can only be established for small parameters. However, when ![]() $b(x)\geq 0$ and a(x) change sign, we cannot derive global results for
$b(x)\geq 0$ and a(x) change sign, we cannot derive global results for ![]() $(\mathcal{P}^\lambda)$ from the results of [Reference De Figueiredo, Gossez and Ubilla26]. Global results for
$(\mathcal{P}^\lambda)$ from the results of [Reference De Figueiredo, Gossez and Ubilla26]. Global results for ![]() $(\mathcal{P}^\lambda)$ were obtained by De Paiva in [Reference De Paiva27] when
$(\mathcal{P}^\lambda)$ were obtained by De Paiva in [Reference De Paiva27] when ![]() $b(x)\geq 0$ and
$b(x)\geq 0$ and ![]() $1 \lt p\leq 2^*-1$.
$1 \lt p\leq 2^*-1$.
Now, suppose that ![]() $(\alpha-1)(\gamma-1)\neq\theta\beta$. Then, for all
$(\alpha-1)(\gamma-1)\neq\theta\beta$. Then, for all ![]() $\overline{\lambda} \gt 0$ and
$\overline{\lambda} \gt 0$ and ![]() $\overline{\mu} \gt 0$, the following system has a solution
$\overline{\mu} \gt 0$, the following system has a solution
 \begin{equation}
\left\{
\begin{array}{lcl}
(\alpha-1) x+\beta y&=&\ln\overline{\lambda}
\\
\theta x+(\gamma-1) y&=&\ln{\overline{\mu}}.
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{lcl}
(\alpha-1) x+\beta y&=&\ln\overline{\lambda}
\\
\theta x+(\gamma-1) y&=&\ln{\overline{\mu}}.
\end{array}
\right.
\end{equation} Then, ![]() $\lambda:=e^{x(1-q)} \gt 0$ and
$\lambda:=e^{x(1-q)} \gt 0$ and ![]() $\mu:=e^{y(1-p)} \gt 0$ satisfy
$\mu:=e^{y(1-p)} \gt 0$ satisfy  $\overline{\lambda}=\lambda^\frac{\alpha-1}{1-q}\mu^\frac{\beta}{1-p}$ and
$\overline{\lambda}=\lambda^\frac{\alpha-1}{1-q}\mu^\frac{\beta}{1-p}$ and  $\overline{\mu}=\lambda^\frac{\theta}{1-q}\mu^\frac{\gamma-1}{1-p}$. Setting
$\overline{\mu}=\lambda^\frac{\theta}{1-q}\mu^\frac{\gamma-1}{1-p}$. Setting  $t=\lambda^\frac{-1}{1-q}$ and
$t=\lambda^\frac{-1}{1-q}$ and  $s=\mu^\frac{-1}{1-p}$, we see that u and v are solutions for
$s=\mu^\frac{-1}{1-p}$, we see that u and v are solutions for ![]() $(\mathcal{P}_1)$ with
$(\mathcal{P}_1)$ with ![]() $\lambda,\mu \gt 0$ if and only if
$\lambda,\mu \gt 0$ if and only if ![]() $\overline{u}=tu$ and
$\overline{u}=tu$ and ![]() $\overline{v}=sv$ are solutions for
$\overline{v}=sv$ are solutions for ![]() $(\mathcal{P}_2)$ with
$(\mathcal{P}_2)$ with ![]() $\overline{\lambda},\overline{\mu} \gt 0$. Therefore, the global results for
$\overline{\lambda},\overline{\mu} \gt 0$. Therefore, the global results for ![]() $(\mathcal{P}_1)$ with certain hypotheses on the weights yield global results for
$(\mathcal{P}_1)$ with certain hypotheses on the weights yield global results for ![]() $(\mathcal{P}_2)$ with the same hypotheses.
$(\mathcal{P}_2)$ with the same hypotheses.
But when the system (1.8) has no solution, this approach does not work. Therefore, even in the case that all weights are non-negative, we cannot obtain a solution ![]() $(u_2,v_2)$ to
$(u_2,v_2)$ to ![]() $(\mathcal{P}_2)$ with
$(\mathcal{P}_2)$ with ![]() $u_2=tu_1$ and
$u_2=tu_1$ and ![]() $v_2=sv_1$ for some
$v_2=sv_1$ for some ![]() $t,s \gt 0$ and
$t,s \gt 0$ and ![]() $(u_1,v_1)$ solution to
$(u_1,v_1)$ solution to ![]() $(\mathcal{P}_1)$. This does not happen in the scalar case, since when the weights are non-negative, global results for
$(\mathcal{P}_1)$. This does not happen in the scalar case, since when the weights are non-negative, global results for ![]() $(\mathcal{P}_\lambda)$ guarantee global results for
$(\mathcal{P}_\lambda)$ guarantee global results for ![]() $(\mathcal{P}^\lambda)$.
$(\mathcal{P}^\lambda)$.
We will see that the conditions ![]() $(PW_1)$–
$(PW_1)$–![]() $(PW_3)$ affect the set of values
$(PW_3)$ affect the set of values ![]() $\lambda,\mu \gt 0$ for which the system has a solution (u, v). Before formalizing the concept of the solution we will employ, it is pertinent to note that since the weight functions lie in
$\lambda,\mu \gt 0$ for which the system has a solution (u, v). Before formalizing the concept of the solution we will employ, it is pertinent to note that since the weight functions lie in ![]() ${L^\infty(\Omega)}$, our optimal expectation is that solutions belong to
${L^\infty(\Omega)}$, our optimal expectation is that solutions belong to ![]() ${C^1(\overline{\Omega})}$. Thus, we shall consider the following definition:
${C^1(\overline{\Omega})}$. Thus, we shall consider the following definition:
Definition 1.1. We will say that ![]() ${(u,v)}$ is a solution to
${(u,v)}$ is a solution to ![]() ${(\mathcal{P}_i)}$ if, for all s > 1,
${(\mathcal{P}_i)}$ if, for all s > 1,  ${u,\,v \in W^{2,s}(\Omega) \cap W^{1,s}_0(\Omega)\cap C^1(\overline{\Omega})}$ and
${u,\,v \in W^{2,s}(\Omega) \cap W^{1,s}_0(\Omega)\cap C^1(\overline{\Omega})}$ and ![]() ${u,\,v}$ satisfy
${u,\,v}$ satisfy ![]() ${(\mathcal{P}_i)}$.
${(\mathcal{P}_i)}$.
Concerning the existence of solutions, throughout this work, we will assume that ![]() ${\Omega \subset \mathbb{R}^N}$ is a bounded domain such that
${\Omega \subset \mathbb{R}^N}$ is a bounded domain such that ![]() ${\partial \Omega \in C^{1,1}}$. Except for the solution of item (v) of Theorem 1.4, this regularity is sufficient to obtain solutions in
${\partial \Omega \in C^{1,1}}$. Except for the solution of item (v) of Theorem 1.4, this regularity is sufficient to obtain solutions in  ${W^{2,s}(\Omega) \cap W^{1,s}_0(\Omega) \cap C^1(\overline{\Omega})}$ for all s > 1. To this end, we will invoke the following classical results from elliptic regularity theory: Theorems 7.26 and 9.15 of [Reference Gilbarg and Trudinger31], which require that
${W^{2,s}(\Omega) \cap W^{1,s}_0(\Omega) \cap C^1(\overline{\Omega})}$ for all s > 1. To this end, we will invoke the following classical results from elliptic regularity theory: Theorems 7.26 and 9.15 of [Reference Gilbarg and Trudinger31], which require that ![]() ${\Omega \subset \mathbb{R}^N}$ be a domain such that
${\Omega \subset \mathbb{R}^N}$ be a domain such that ![]() ${\partial \Omega\in C^{0,1}}$ and
${\partial \Omega\in C^{0,1}}$ and ![]() ${\partial \Omega\in C^{1,1}}$, respectively. Regarding the non-existence of solutions, we require the existence of
${\partial \Omega\in C^{1,1}}$, respectively. Regarding the non-existence of solutions, we require the existence of ![]() ${\Omega_0 \subset \Omega}$ such that
${\Omega_0 \subset \Omega}$ such that ![]() ${\partial \Omega_0 \in C^{1,1}}$, so that we can use Green’s identities (which require
${\partial \Omega_0 \in C^{1,1}}$, so that we can use Green’s identities (which require ![]() ${\partial \Omega_0 \in C^1}$) and the results of [Reference Gilbarg and Trudinger31, Theorems 9.15 and Lemma 9.17] in Proposition 2.7 (which require
${\partial \Omega_0 \in C^1}$) and the results of [Reference Gilbarg and Trudinger31, Theorems 9.15 and Lemma 9.17] in Proposition 2.7 (which require ![]() ${\partial \Omega_0 \in C^{1,1}})$.
${\partial \Omega_0 \in C^{1,1}})$.
Let ![]() $\Omega_0\subset\Omega$ be open and connected. We say that a function
$\Omega_0\subset\Omega$ be open and connected. We say that a function ![]() $h:\overline{\Omega}\rightarrow\mathbb{R}$ satisfies the condition
$h:\overline{\Omega}\rightarrow\mathbb{R}$ satisfies the condition ![]() $(P_{\Omega_0})$ if
$(P_{\Omega_0})$ if ![]() $h(x)\geq 0$ for all
$h(x)\geq 0$ for all ![]() $x\in\Omega_0$, and the set
$x\in\Omega_0$, and the set ![]() $\{x\in\Omega_0\,\,|\,\,h(x) \gt 0\}$ has positive Lebesgue measure. The conditions on the weights are stated below.
$\{x\in\Omega_0\,\,|\,\,h(x) \gt 0\}$ has positive Lebesgue measure. The conditions on the weights are stated below.
(P1)
 $a,b,c,d\in L^\infty(\Omega)\setminus\{0\}$;
$a,b,c,d\in L^\infty(\Omega)\setminus\{0\}$;(P2)
 $a(x)\geq 0$ and
$a(x)\geq 0$ and  $b(x)\geq 0$ in Ω;
$b(x)\geq 0$ in Ω;
Regarding condition ![]() $(P_1)$, we do not know if the results of the present work are valid for the case where the weight functions are in an appropriate Lp space. We have not delved into this issue.
$(P_1)$, we do not know if the results of the present work are valid for the case where the weight functions are in an appropriate Lp space. We have not delved into this issue.
Certain constants will appear in the form of powers associated with the questions of existence and non-existence. To better organize the presentation of our first theorem, we present these constants in the table below.

In our first result, we show that there exist ![]() $\tau,\sigma,\overline{\tau},\overline{\sigma}\geq0$ satisfying
$\tau,\sigma,\overline{\tau},\overline{\sigma}\geq0$ satisfying ![]() $\tau+\sigma \gt 0$,
$\tau+\sigma \gt 0$, ![]() $\overline{\tau}+\overline{\sigma} \gt 0$, and
$\overline{\tau}+\overline{\sigma} \gt 0$, and ![]() $\Lambda^*_1,\Lambda^*_2 \gt 0$ such that problem
$\Lambda^*_1,\Lambda^*_2 \gt 0$ such that problem ![]() $(\mathcal{P}_1)$ has no solution if
$(\mathcal{P}_1)$ has no solution if ![]() $\lambda^\tau\mu^\sigma \gt \Lambda^*_1$ or
$\lambda^\tau\mu^\sigma \gt \Lambda^*_1$ or ![]() $\lambda^{\overline{\tau}}\mu^{\overline{\sigma}} \gt \Lambda^*_2$. The same occurs with
$\lambda^{\overline{\tau}}\mu^{\overline{\sigma}} \gt \Lambda^*_2$. The same occurs with ![]() $(\mathcal{P}_2)$. Specifically, we prove the following:
$(\mathcal{P}_2)$. Specifically, we prove the following:
Theorem 1.2 (Non-existence)
Consider the system ![]() $(\mathcal{P}_i)$, where
$(\mathcal{P}_i)$, where ![]() ${\Omega\subset\mathbb{R}^N}$ is a bounded domain, and suppose that the weights
${\Omega\subset\mathbb{R}^N}$ is a bounded domain, and suppose that the weights ![]() $a(\cdot)$,
$a(\cdot)$, ![]() $b(\cdot)$,
$b(\cdot)$, ![]() $c(\cdot)$,
$c(\cdot)$, ![]() $d(\cdot)$ satisfy the
$d(\cdot)$ satisfy the ![]() $(P_{\Omega_0})$ condition for some
$(P_{\Omega_0})$ condition for some ![]() $C^{1,1}$ domain
$C^{1,1}$ domain ![]() $\Omega_0\subset\Omega$, and that
$\Omega_0\subset\Omega$, and that ![]() $(PW_j)$ holds. Then, there are positive numbers
$(PW_j)$ holds. Then, there are positive numbers ![]() $\Lambda_{1ij}^* \gt 0$ and
$\Lambda_{1ij}^* \gt 0$ and ![]() $\Lambda_{2ij}^* \gt 0$, possibly depending on
$\Lambda_{2ij}^* \gt 0$, possibly depending on ![]() $a(\cdot)$,
$a(\cdot)$, ![]() $b(\cdot)$,
$b(\cdot)$, ![]() $c(\cdot)$,
$c(\cdot)$, ![]() $d(\cdot)$, α, β, γ, θ, Ω0, Ω, such that there are no solutions (u, v) for
$d(\cdot)$, α, β, γ, θ, Ω0, Ω, such that there are no solutions (u, v) for ![]() $(\mathcal{P}_i)$ in the sense of Definition 1.1, with u > 0 and v > 0 in Ω0 when
$(\mathcal{P}_i)$ in the sense of Definition 1.1, with u > 0 and v > 0 in Ω0 when ![]() $\lambda^{\tau_{ij}}\mu^{\sigma_{ij}} \gt \Lambda_{1ij}^*$ or
$\lambda^{\tau_{ij}}\mu^{\sigma_{ij}} \gt \Lambda_{1ij}^*$ or  $\lambda^{\overline{\tau}_{ij}}\mu^{\overline{\sigma}_{ij}} \gt \Lambda_{2ij}^*$.
$\lambda^{\overline{\tau}_{ij}}\mu^{\overline{\sigma}_{ij}} \gt \Lambda_{2ij}^*$.
In [Reference Ambrosetti, Brézis and Cerami4], the non-existence of positive solutions to ![]() $(\mathcal{P}_\lambda)$ is a consequence of the simple inequality: Given c > 0, there exists
$(\mathcal{P}_\lambda)$ is a consequence of the simple inequality: Given c > 0, there exists ![]() $\lambda=\lambda_c \gt 0$ such that
$\lambda=\lambda_c \gt 0$ such that ![]() $\lambda t^q+t^p \gt ct$,
$\lambda t^q+t^p \gt ct$, ![]() $\forall \,t \gt 0$ (see [Reference Ambrosetti, Brézis and Cerami4, (3.1) with
$\forall \,t \gt 0$ (see [Reference Ambrosetti, Brézis and Cerami4, (3.1) with ![]() $c=\lambda_1(\Omega)$]). However, even for the case
$c=\lambda_1(\Omega)$]). However, even for the case ![]() $f_\lambda=\lambda t^q \,+\, t^\alpha s^\beta$ and
$f_\lambda=\lambda t^q \,+\, t^\alpha s^\beta$ and ![]() $g_\mu=\mu s^p \,+\, t^\theta s^\gamma$, for all
$g_\mu=\mu s^p \,+\, t^\theta s^\gamma$, for all ![]() $\lambda,\mu \gt 0$, there is no c > 0 satisfying
$\lambda,\mu \gt 0$, there is no c > 0 satisfying ![]() $f_\lambda(x,t,s) \gt ct$ and
$f_\lambda(x,t,s) \gt ct$ and ![]() $g_\mu(x,t,s) \gt cs$ simultaneously for all
$g_\mu(x,t,s) \gt cs$ simultaneously for all ![]() $t,s \gt 0$. Hence, the approach for the non-existence of solutions is different in the context of systems. Lemma 2.1 plays a key role in our proof. It is a slight adaptation of [Reference Ambrosetti, Brézis and Cerami4, Lemma 3.3]. (Observe that in the work [Reference Ambrosetti, Brézis and Cerami4], this lemma is not relevant to show the result of non-existence.) Our proof is based on technical arguments, and in some cases, we use the Krein–Rutman theorem [Reference Krein and Rutman37].
$t,s \gt 0$. Hence, the approach for the non-existence of solutions is different in the context of systems. Lemma 2.1 plays a key role in our proof. It is a slight adaptation of [Reference Ambrosetti, Brézis and Cerami4, Lemma 3.3]. (Observe that in the work [Reference Ambrosetti, Brézis and Cerami4], this lemma is not relevant to show the result of non-existence.) Our proof is based on technical arguments, and in some cases, we use the Krein–Rutman theorem [Reference Krein and Rutman37].
The problem ![]() $(\mathcal{P}_2)$ is related to
$(\mathcal{P}_2)$ is related to ![]() $(\mathcal{P}^\lambda)$. In [Reference De Paiva27, Theorem 1], the author showed a global non-existence result when
$(\mathcal{P}^\lambda)$. In [Reference De Paiva27, Theorem 1], the author showed a global non-existence result when ![]() $0 \lt q \lt 1 \lt p\leq 2^*-1$,
$0 \lt q \lt 1 \lt p\leq 2^*-1$, ![]() $b(x)\geq 0$ in Ω, and
$b(x)\geq 0$ in Ω, and ![]() $\overline{\{x\in\Omega\,\,|\,\,a(x) \gt 0\}}\cap\overline{\{x\in\Omega\,\,|\,\,a(x) \lt 0\}}=\emptyset$ with other conditions. Therefore, concerning the non-existence question, Theorem 1.2 complements this result since the hypotheses considered are weaker than [Reference De Paiva27, Theorem 1] and we are considering supercritical powers, that is,
$\overline{\{x\in\Omega\,\,|\,\,a(x) \gt 0\}}\cap\overline{\{x\in\Omega\,\,|\,\,a(x) \lt 0\}}=\emptyset$ with other conditions. Therefore, concerning the non-existence question, Theorem 1.2 complements this result since the hypotheses considered are weaker than [Reference De Paiva27, Theorem 1] and we are considering supercritical powers, that is, ![]() $\alpha+\beta \gt 2^*-1$ or
$\alpha+\beta \gt 2^*-1$ or ![]() $\theta+\gamma \gt 2^*-1$ in
$\theta+\gamma \gt 2^*-1$ in ![]() $(\mathcal{P}_2)$.
$(\mathcal{P}_2)$.
Definition 1.3. We say that (u, v) satisfying ![]() $(\mathcal{P}_i)$, in the sense of Definition 1.1, is a minimal positive solution when u > 0 and v > 0 in Ω. Moreover, if
$(\mathcal{P}_i)$, in the sense of Definition 1.1, is a minimal positive solution when u > 0 and v > 0 in Ω. Moreover, if ![]() $u^* \gt 0$ and
$u^* \gt 0$ and ![]() $v^* \gt 0$ in Ω, and
$v^* \gt 0$ in Ω, and ![]() $(u^*,v^*)$ is another solution for
$(u^*,v^*)$ is another solution for ![]() $(\mathcal{P}_i)$, then
$(\mathcal{P}_i)$, then ![]() $u\leq u^*$ and
$u\leq u^*$ and ![]() $v\leq v^*$ in Ω.
$v\leq v^*$ in Ω.
In order to present our next theorem, we define the following hypothesis:
 \begin{equation*}
\begin{array}{ll}
(H_1) c(x)\geq 0 \mbox{ in } \Omega; & (H_4) d(x)\geq 0 \mbox{ in } \Omega; \\
(H_2) \alpha\geq 1; & (H_5) \gamma\geq 1; \\
(H_3) q \lt \alpha \lt 1 \mbox{ and } \inf\limits_\Omega a(x) \gt 0; & (H_6) p \lt \gamma \lt 1 \mbox{ and } \inf\limits_\Omega b(x) \gt 0. \\
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ll}
(H_1) c(x)\geq 0 \mbox{ in } \Omega; & (H_4) d(x)\geq 0 \mbox{ in } \Omega; \\
(H_2) \alpha\geq 1; & (H_5) \gamma\geq 1; \\
(H_3) q \lt \alpha \lt 1 \mbox{ and } \inf\limits_\Omega a(x) \gt 0; & (H_6) p \lt \gamma \lt 1 \mbox{ and } \inf\limits_\Omega b(x) \gt 0. \\
\end{array}
\end{equation*} In our second result, in the main item, we show that there exist ![]() $\tau,\sigma,\overline{\tau},\overline{\sigma}\geq0$ satisfying
$\tau,\sigma,\overline{\tau},\overline{\sigma}\geq0$ satisfying ![]() $\tau+\sigma \gt 0$,
$\tau+\sigma \gt 0$, ![]() $\overline{\tau}+\overline{\sigma} \gt 0$, and
$\overline{\tau}+\overline{\sigma} \gt 0$, and ![]() $\Lambda_1,\Lambda_2 \gt 0$ such that problem
$\Lambda_1,\Lambda_2 \gt 0$ such that problem ![]() $(\mathcal{P}_1)$ has at least one solution if
$(\mathcal{P}_1)$ has at least one solution if ![]() $\lambda^\tau\mu^\sigma\leq\Lambda_1$ and
$\lambda^\tau\mu^\sigma\leq\Lambda_1$ and ![]() $\lambda^{\overline{\tau}}\mu^{\overline{\sigma}}\leq\Lambda_2$. The same occurs with
$\lambda^{\overline{\tau}}\mu^{\overline{\sigma}}\leq\Lambda_2$. The same occurs with ![]() $(\mathcal{P}_2)$. Specifically, we prove the following:
$(\mathcal{P}_2)$. Specifically, we prove the following:
Theorem 1.4 (Positive Solution)
Consider the system ![]() $(\mathcal{P}_i)$ with
$(\mathcal{P}_i)$ with ![]() ${\Omega\subset\mathbb{R}^N}$ being a
${\Omega\subset\mathbb{R}^N}$ being a ![]() ${C^{1,1}}$ bounded domain. Suppose that
${C^{1,1}}$ bounded domain. Suppose that ![]() $(PW_j)$ and
$(PW_j)$ and ![]() $(P_1)$–
$(P_1)$–![]() $(P_2)$ hold. In regard to the existence of solutions for
$(P_2)$ hold. In regard to the existence of solutions for ![]() ${(\mathcal{P}_i)}$ in the sense of Definition 1.1, there are positive numbers
${(\mathcal{P}_i)}$ in the sense of Definition 1.1, there are positive numbers ![]() $\Lambda_{1ij} \gt 0$ and
$\Lambda_{1ij} \gt 0$ and ![]() $\Lambda_{2ij} \gt 0$, possibly depending on
$\Lambda_{2ij} \gt 0$, possibly depending on ![]() $a(\cdot), b(\cdot), c(\cdot), d(\cdot), p, q, \alpha, \beta, \gamma, \theta, \Omega$, such that:
$a(\cdot), b(\cdot), c(\cdot), d(\cdot), p, q, \alpha, \beta, \gamma, \theta, \Omega$, such that:
(i) Suppose that
 $(H_l)$ and
$(H_l)$ and  $(H_k)$ hold with
$(H_k)$ hold with  $1\leq l\leq 3$ and
$1\leq l\leq 3$ and  $4\leq k\leq 6$. Then
$4\leq k\leq 6$. Then  $(\mathcal{P}_i)$ has a positive solution when
$(\mathcal{P}_i)$ has a positive solution when  $\lambda^{\tau_{ij}}\mu^{\sigma_{ij}}\leq \Lambda_{1ij}$ and
$\lambda^{\tau_{ij}}\mu^{\sigma_{ij}}\leq \Lambda_{1ij}$ and  $\lambda^{\overline{\tau}_{ij}}\mu^{\overline{\sigma}_{ij}}\leq \Lambda_{2ij}$;
$\lambda^{\overline{\tau}_{ij}}\mu^{\overline{\sigma}_{ij}}\leq \Lambda_{2ij}$;(ii) If
 $c(x) \geq 0$ and
$c(x) \geq 0$ and  $d(x) \geq 0$ in Ω, there exists
$d(x) \geq 0$ in Ω, there exists  $0 \lt L^*_{ij} \leq +\infty$ such that for all
$0 \lt L^*_{ij} \leq +\infty$ such that for all  $\lambda \in (0, L^*_{ij})$, there is
$\lambda \in (0, L^*_{ij})$, there is  $0 \lt \Lambda_\lambda \lt +\infty$ such that for all
$0 \lt \Lambda_\lambda \lt +\infty$ such that for all  $\mu \in (0, \Lambda_\lambda)$, problem
$\mu \in (0, \Lambda_\lambda)$, problem  $(\mathcal{P}_i)$ has a minimal positive solution. If
$(\mathcal{P}_i)$ has a minimal positive solution. If  $\mu \in (\Lambda_\lambda, +\infty)$, then there is no positive solution for
$\mu \in (\Lambda_\lambda, +\infty)$, then there is no positive solution for  $(\mathcal{P}_i)$. Moreover,
$(\mathcal{P}_i)$. Moreover,  $L^*_{11} = L^*_{22} = +\infty$, and
$L^*_{11} = L^*_{22} = +\infty$, and  $L^*_{ij} \lt +\infty$ for the other cases;
$L^*_{ij} \lt +\infty$ for the other cases;(iii) If
 $c(x)\geq 0$ and
$c(x)\geq 0$ and  $d(x)\geq 0$ in Ω, there exists
$d(x)\geq 0$ in Ω, there exists  $0 \lt M^*_{ij} \leq +\infty$ such that for all
$0 \lt M^*_{ij} \leq +\infty$ such that for all  $\mu \in (0, M^*_{ij})$, there is
$\mu \in (0, M^*_{ij})$, there is  $\Lambda_\mu$ such that for all
$\Lambda_\mu$ such that for all  $\lambda \in (0, \Lambda_\mu)$, problem
$\lambda \in (0, \Lambda_\mu)$, problem  $(\mathcal{P}_i)$ has a minimal positive solution. If
$(\mathcal{P}_i)$ has a minimal positive solution. If  $\lambda \in (\Lambda_\mu, +\infty)$, then there is no positive solution for
$\lambda \in (\Lambda_\mu, +\infty)$, then there is no positive solution for  $(\mathcal{P}_i)$. Moreover,
$(\mathcal{P}_i)$. Moreover,  $M^*_{11} = M^*_{22} = M^*_{13} = M^*_{23} = +\infty$, and
$M^*_{11} = M^*_{22} = M^*_{13} = M^*_{23} = +\infty$, and  $M^*_{ij} \lt +\infty$ for the other cases;
$M^*_{ij} \lt +\infty$ for the other cases;(iv) If
 $c(x) \geq 0$ and
$c(x) \geq 0$ and  $d(x) \geq 0$ in Ω, and
$d(x) \geq 0$ in Ω, and  $(u_{\lambda\mu},v_{\lambda\mu})$ is a minimal positive solution for
$(u_{\lambda\mu},v_{\lambda\mu})$ is a minimal positive solution for  $(\mathcal{P}_i)$ with the parameters
$(\mathcal{P}_i)$ with the parameters  $\lambda, \mu \gt 0$, then for all
$\lambda, \mu \gt 0$, then for all  $0 \lt \lambda_1 \leq \lambda$ and
$0 \lt \lambda_1 \leq \lambda$ and  $0 \lt \mu_1 \leq \mu$, problem
$0 \lt \mu_1 \leq \mu$, problem  $(\mathcal{P}_i)$ has a minimal positive solution
$(\mathcal{P}_i)$ has a minimal positive solution  $(u_{\lambda_1\mu_1},v_{\lambda_1\mu_1})$ with the parameters
$(u_{\lambda_1\mu_1},v_{\lambda_1\mu_1})$ with the parameters  $\lambda_1, \mu_1 \gt 0$. Moreover,
$\lambda_1, \mu_1 \gt 0$. Moreover,  $u_{\lambda_1\mu_1} \leq u_{\lambda\mu}$ and
$u_{\lambda_1\mu_1} \leq u_{\lambda\mu}$ and  $v_{\lambda_1\mu_1} \leq v_{\lambda\mu}$ in Ω.
$v_{\lambda_1\mu_1} \leq v_{\lambda\mu}$ in Ω.(v) Suppose that
 $c(x)\geq 0$ and
$c(x)\geq 0$ and  $d(x)\geq 0$ in Ω. Then, if α > 1 and γ > 1, we have a positive weak solution for
$d(x)\geq 0$ in Ω. Then, if α > 1 and γ > 1, we have a positive weak solution for  $(\mathcal{P}_i)$ when
$(\mathcal{P}_i)$ when  $\lambda\in(0,L^*_{ij})$ and
$\lambda\in(0,L^*_{ij})$ and  $\mu=\Lambda_\lambda$. Similarly, we have a positive weak solution for
$\mu=\Lambda_\lambda$. Similarly, we have a positive weak solution for  $(\mathcal{P}_i)$ when
$(\mathcal{P}_i)$ when  $\mu\in(0,L^*_{ij})$ and
$\mu\in(0,L^*_{ij})$ and  $\lambda=\Lambda_\mu$.
$\lambda=\Lambda_\mu$.
With the purpose of exemplifying the previous theorem, let us consider the following system:
 \begin{equation}
\left\{
\begin{array}{ll}
-\Delta u=\lambda u^q+u^\alpha v^\beta & \mbox{in}~~\Omega
\\
-\Delta v=\mu u^p+u^\theta v^\gamma & \mbox{in}~~\Omega
\\
u \gt 0,\,\,v \gt 0& \mbox{in}~~\Omega
\\
u=v=0&\mbox{on}~~\partial\Omega.
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{ll}
-\Delta u=\lambda u^q+u^\alpha v^\beta & \mbox{in}~~\Omega
\\
-\Delta v=\mu u^p+u^\theta v^\gamma & \mbox{in}~~\Omega
\\
u \gt 0,\,\,v \gt 0& \mbox{in}~~\Omega
\\
u=v=0&\mbox{on}~~\partial\Omega.
\end{array}
\right.
\end{equation} Supposing that ![]() $p,q\in(0,1)$ and
$p,q\in(0,1)$ and ![]() $\lambda,\mu \gt 0$. Regarding existence, Theorem 1.4-(i) ensures the existence of
$\lambda,\mu \gt 0$. Regarding existence, Theorem 1.4-(i) ensures the existence of ![]() $\Lambda_i \gt 0$ such that:
$\Lambda_i \gt 0$ such that:
(E1) Assuming that
 $\alpha\geq1,\,\gamma\geq 1,\,\beta \gt 0,\,\theta \gt 0$, then Equation (1.9) has a solution if:
$\alpha\geq1,\,\gamma\geq 1,\,\beta \gt 0,\,\theta \gt 0$, then Equation (1.9) has a solution if:
 \begin{equation*}
\lambda^\frac{\alpha-1}{1-q}\mu^\frac{\beta}{1-p}\leq\Lambda_1
\,\,\,\mbox{and}\,\,
\lambda^\frac{\theta}{1-q}\mu^\frac{\gamma-1}{1-p}\leq\Lambda_2
\end{equation*}
\begin{equation*}
\lambda^\frac{\alpha-1}{1-q}\mu^\frac{\beta}{1-p}\leq\Lambda_1
\,\,\,\mbox{and}\,\,
\lambda^\frac{\theta}{1-q}\mu^\frac{\gamma-1}{1-p}\leq\Lambda_2
\end{equation*}(E2) Assuming that
 $0 \lt \alpha \lt 1 \lt \beta$ and
$0 \lt \alpha \lt 1 \lt \beta$ and  $0 \lt \gamma \lt 1 \lt \theta$, then Equation (1.9) has a solution if:
$0 \lt \gamma \lt 1 \lt \theta$, then Equation (1.9) has a solution if:
 \begin{equation*}
\lambda\leq \Lambda_1\,\,\,\mbox{and}\,\,\,\mu\leq\Lambda_2
\end{equation*}
\begin{equation*}
\lambda\leq \Lambda_1\,\,\,\mbox{and}\,\,\,\mu\leq\Lambda_2
\end{equation*}(E3) Assuming that
 $\alpha\geq 1$, β > 0, and
$\alpha\geq 1$, β > 0, and  $0 \lt \gamma \lt 1 \lt \theta$, then Equation (1.9) has a solution if:
$0 \lt \gamma \lt 1 \lt \theta$, then Equation (1.9) has a solution if:
 \begin{equation*}
\lambda\leq\Lambda_1\,\,\,\mbox{and}\,\,\,\lambda^\frac{\alpha-1}{1-q}\mu^\frac{\beta}{1-p}
\leq\Lambda_2.
\end{equation*}
\begin{equation*}
\lambda\leq\Lambda_1\,\,\,\mbox{and}\,\,\,\lambda^\frac{\alpha-1}{1-q}\mu^\frac{\beta}{1-p}
\leq\Lambda_2.
\end{equation*}
Note that if α > 1 or γ > 1, then the result of ![]() $(E_1)$ ensures that the set
$(E_1)$ ensures that the set ![]() $\mathcal{E}:=$
$\mathcal{E}:=$ ![]() $\{(\lambda,\mu)\in\mathbb{R}^2_+ |$ (1.9)
$\{(\lambda,\mu)\in\mathbb{R}^2_+ |$ (1.9) ![]() $\mbox{has a solution}\,\}$ is unbounded. Furthermore, if α > 1, then the result of
$\mbox{has a solution}\,\}$ is unbounded. Furthermore, if α > 1, then the result of ![]() $(E_3)$ also implies that
$(E_3)$ also implies that ![]() $\mathcal{E}$ is unbounded. These results contrast with the scalar case, since
$\mathcal{E}$ is unbounded. These results contrast with the scalar case, since ![]() $\left\{\lambda\in\mathbb{R}_+\,\,|\,\,{(\mathcal{P}_\lambda)}\,\,\mbox{has a solution}\,\right\}=(0,\Lambda]$ and
$\left\{\lambda\in\mathbb{R}_+\,\,|\,\,{(\mathcal{P}_\lambda)}\,\,\mbox{has a solution}\,\right\}=(0,\Lambda]$ and ![]() $\Lambda \lt +\infty$ for the case where the weight functions of
$\Lambda \lt +\infty$ for the case where the weight functions of ![]() $(\mathcal{P}_\lambda)$ are constants.
$(\mathcal{P}_\lambda)$ are constants.
To prove Theorem 1.4, we use the sub-super solution method. The way we define the concept of sub-super solution for systems is somewhat different than in the scalar case. For example, a solution of ![]() $(\mathcal{P}_i)$ may not be a sub-solution or a super-solution for
$(\mathcal{P}_i)$ may not be a sub-solution or a super-solution for ![]() $(\mathcal{P}_i)$ (see Remarks 3.1 and 3.5).
$(\mathcal{P}_i)$ (see Remarks 3.1 and 3.5).
The super-solutions are obtained by solving the systems Equation (3.1) and (3.2). The greatest difficulty lies in obtaining solutions when one of the parameters λ > 0 or µ > 0 can be arbitrarily large. The sub-solutions come in two types of functions. To obtain the first, we use the theory of principal eigenfunction for operators with indefinite weight functions. For that, we choose an appropriate weight function (see, for instance, Equation (3.4)). To obtain the second sub-solution, we solve an auxiliary problem employing variational techniques (see Proposition 3.6).
The novelty of this theorem lies in the fact that we solve the problem of the existence of a solution for a more general class of systems (not just gradient systems and not just with critical or subcritical growth powers), and we prove that the set of solutions  $\mathcal{O}_i:=\left\{(\lambda,\mu)\in\mathbb{R}_+^2\,\,|\,\,(\mathcal{P}_i)\,\,\mbox{has solution}\,\right\}$ is unbounded in some cases. To prove (v), we use the same approach as in [Reference Ambrosetti, Brézis and Cerami4, p. 528]. However, the same idea does not work when
$\mathcal{O}_i:=\left\{(\lambda,\mu)\in\mathbb{R}_+^2\,\,|\,\,(\mathcal{P}_i)\,\,\mbox{has solution}\,\right\}$ is unbounded in some cases. To prove (v), we use the same approach as in [Reference Ambrosetti, Brézis and Cerami4, p. 528]. However, the same idea does not work when ![]() $\alpha\leq 1$ or
$\alpha\leq 1$ or ![]() $\gamma\leq 1$, although we believe that this statement holds for other cases. Unfortunately, we cannot prove it. Despite this, in [Reference Da Silva23], we have a complete proof for when the system is of the gradient type.
$\gamma\leq 1$, although we believe that this statement holds for other cases. Unfortunately, we cannot prove it. Despite this, in [Reference Da Silva23], we have a complete proof for when the system is of the gradient type.
Originally, this work contained a study involving the multiplicity of solutions for gradient-type systems, as well as analyzing cases where all weights change sign and the nonlinearities have supercritical growth terms. However, we decided to address this in another paper [Reference Da Silva23]. The issue of local minimization for functionals with two variables was also addressed in another paper [Reference Da Silva24]. However, the question of multiplicity for a system that is not of the gradient type remains open. A major difficulty is that if the system cannot be studied via variational methods, we do not know how to approach the issue of multiplicity. Unfortunately, we were unable to answer some other questions. For example, can we have the maps ![]() $\mu\mapsto\Lambda_\mu$ and
$\mu\mapsto\Lambda_\mu$ and ![]() $\lambda\mapsto\Lambda_\lambda$ continuous? Is it possible that
$\lambda\mapsto\Lambda_\lambda$ continuous? Is it possible that ![]() $\Lambda_{1ij}=\Lambda^*_{1ij}$ and
$\Lambda_{1ij}=\Lambda^*_{1ij}$ and ![]() $\Lambda_{2ij}=\Lambda^*_{2ij}$? If
$\Lambda_{2ij}=\Lambda^*_{2ij}$? If ![]() $0 \lt \lambda=L^*_{ij} \lt +\infty$, can we have
$0 \lt \lambda=L^*_{ij} \lt +\infty$, can we have ![]() $\Lambda_\lambda \gt 0$? If
$\Lambda_\lambda \gt 0$? If ![]() $0 \lt \mu=M^*_{ij} \lt +\infty$, can we have
$0 \lt \mu=M^*_{ij} \lt +\infty$, can we have ![]() $\Lambda_\mu \gt 0$?
$\Lambda_\mu \gt 0$?
After the introduction, this work is divided into three other sections. The second section is dedicated to the question of non-existence of solutions for ![]() $(\mathcal{P}_i)$. In the third section, we present the method of sub-super solution, and finally, in the fourth and last section, we present the proof of Theorem 1.4.
$(\mathcal{P}_i)$. In the third section, we present the method of sub-super solution, and finally, in the fourth and last section, we present the proof of Theorem 1.4.
2. Non-existence results
This section is dedicated to non-existence issues for the problems ![]() $(\mathcal{P}_1)$ and
$(\mathcal{P}_1)$ and ![]() $(\mathcal{P}_2)$. The proof of the following lemma is an adaptation of [Reference Ambrosetti, Brézis and Cerami4, Lemma 3.3].
$(\mathcal{P}_2)$. The proof of the following lemma is an adaptation of [Reference Ambrosetti, Brézis and Cerami4, Lemma 3.3].
Lemma 2.1. Let ![]() $\Omega_0\subset\mathbb{R}^N$ be a C 1 bounded domain,
$\Omega_0\subset\mathbb{R}^N$ be a C 1 bounded domain, ![]() $m\in L^\infty(\Omega_0)$ which satisfies
$m\in L^\infty(\Omega_0)$ which satisfies ![]() $0\leq m(x)\not\equiv 0$ in Ω0, assume that f(t) is a function such that
$0\leq m(x)\not\equiv 0$ in Ω0, assume that f(t) is a function such that ![]() $t^{-1}f(t)$ is decreasing for t > 0. Suppose that
$t^{-1}f(t)$ is decreasing for t > 0. Suppose that ![]() $\phi,\,\varphi\in W^{2,s}(\Omega_0)\cap C^1(\overline{\Omega}_0)$ and
$\phi,\,\varphi\in W^{2,s}(\Omega_0)\cap C^1(\overline{\Omega}_0)$ and ![]() $Q \gt -\lambda_1(\Omega_0)$ satisfies
$Q \gt -\lambda_1(\Omega_0)$ satisfies
 \begin{equation*}
\left\{
\begin{array}{lll}
-\Delta \varphi+Q\varphi\geq m(x)f(\varphi),&x\in\Omega_0\\
\varphi \gt 0 ,&x\in\Omega_0
\end{array}
\right.
\,\,\,\,\mbox{and}\,\,\,\,
\left\{
\begin{array}{lll}
-\Delta \phi+Q\phi\leq m(x)f(\phi),&x\in\Omega_0\\
\phi \gt 0,&x\in\Omega_0\\
\phi=0,&x\in\partial\Omega_0
\end{array}
\right.
\end{equation*}
\begin{equation*}
\left\{
\begin{array}{lll}
-\Delta \varphi+Q\varphi\geq m(x)f(\varphi),&x\in\Omega_0\\
\varphi \gt 0 ,&x\in\Omega_0
\end{array}
\right.
\,\,\,\,\mbox{and}\,\,\,\,
\left\{
\begin{array}{lll}
-\Delta \phi+Q\phi\leq m(x)f(\phi),&x\in\Omega_0\\
\phi \gt 0,&x\in\Omega_0\\
\phi=0,&x\in\partial\Omega_0
\end{array}
\right.
\end{equation*} then ![]() $\varphi\geq\phi$ in Ω0.
$\varphi\geq\phi$ in Ω0.
Proof. Let ![]() $\Theta\in C^1(\mathbb{R})$ be a nondecreasing function such that
$\Theta\in C^1(\mathbb{R})$ be a nondecreasing function such that ![]() $\Theta(t)=0$ for
$\Theta(t)=0$ for ![]() $t\leq 0$ and
$t\leq 0$ and ![]() $\Theta(x)=1$ for
$\Theta(x)=1$ for ![]() $t\geq 1$. Setting
$t\geq 1$. Setting  $\Theta_\varepsilon(t)=\Theta(\frac{t}{\varepsilon})$, as
$\Theta_\varepsilon(t)=\Theta(\frac{t}{\varepsilon})$, as ![]() ${\Omega_0}$ is a
${\Omega_0}$ is a ![]() ${C^1}$ bounded domain, we can then invoke the Green’s formula and proceed as in [Reference Ambrosetti, Brézis and Cerami4, Lemma 3.3] to get
${C^1}$ bounded domain, we can then invoke the Green’s formula and proceed as in [Reference Ambrosetti, Brézis and Cerami4, Lemma 3.3] to get
 \begin{equation*}
\begin{array}{lll}
\int_{\Omega_0}m(x)\phi\varphi\left[\dfrac{f(\varphi)}{\varphi}
-\dfrac{f(\phi)}{\phi}\right]\Theta_\varepsilon(\phi-\varphi)\leq-\int_{\Omega_0}\widehat{\Theta}_\varepsilon(\phi-\varphi)\Delta\phi,
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lll}
\int_{\Omega_0}m(x)\phi\varphi\left[\dfrac{f(\varphi)}{\varphi}
-\dfrac{f(\phi)}{\phi}\right]\Theta_\varepsilon(\phi-\varphi)\leq-\int_{\Omega_0}\widehat{\Theta}_\varepsilon(\phi-\varphi)\Delta\phi,
\end{array}
\end{equation*} where  $\widehat{\Theta}_\varepsilon(t):=\int_0^ts \Theta'_\varepsilon(s)ds$. Since
$\widehat{\Theta}_\varepsilon(t):=\int_0^ts \Theta'_\varepsilon(s)ds$. Since  $0\leq \widehat{\Theta}_\varepsilon(t)\leq\varepsilon$, then
$0\leq \widehat{\Theta}_\varepsilon(t)\leq\varepsilon$, then
 \begin{equation*}
0\leq\int_{\Omega_0}m(x)\phi\varphi\left[\dfrac{f(\varphi)}{\varphi}
-\dfrac{f(\phi)}{\phi}\right]\Theta_\varepsilon(\phi-\varphi)dx\leq\varepsilon
\left(-\int_{\Omega_0}\Delta\phi\right).
\end{equation*}
\begin{equation*}
0\leq\int_{\Omega_0}m(x)\phi\varphi\left[\dfrac{f(\varphi)}{\varphi}
-\dfrac{f(\phi)}{\phi}\right]\Theta_\varepsilon(\phi-\varphi)dx\leq\varepsilon
\left(-\int_{\Omega_0}\Delta\phi\right).
\end{equation*} Since ![]() $t^{-1}f(t)$ is decreasing for t > 0, taking
$t^{-1}f(t)$ is decreasing for t > 0, taking ![]() $\varepsilon\rightarrow 0^+$ in the above expression, we obtain that
$\varepsilon\rightarrow 0^+$ in the above expression, we obtain that
 \begin{equation*}
\int_{\Omega_1}m(x)\phi\varphi\left[\dfrac{f(\varphi)}{\varphi}
-\dfrac{f(\phi)}{\phi}\right]dx=0
\end{equation*}
\begin{equation*}
\int_{\Omega_1}m(x)\phi\varphi\left[\dfrac{f(\varphi)}{\varphi}
-\dfrac{f(\phi)}{\phi}\right]dx=0
\end{equation*} where ![]() $\Omega_1:=\left\{x\in\Omega_0\,\,|\,\,\phi(x) \gt \varphi(x)\right\}\subset\subset\Omega_0$, which is an open set. Since
$\Omega_1:=\left\{x\in\Omega_0\,\,|\,\,\phi(x) \gt \varphi(x)\right\}\subset\subset\Omega_0$, which is an open set. Since ![]() $t^{-1}f(t)$ is decreasing for t > 0, if
$t^{-1}f(t)$ is decreasing for t > 0, if ![]() $\Omega_1\neq\emptyset$, we have that
$\Omega_1\neq\emptyset$, we have that ![]() $m(x)=0 \,\,\forall x\in\Omega_1$, so
$m(x)=0 \,\,\forall x\in\Omega_1$, so ![]() $-\Delta(\varphi-\phi)+Q(\varphi-\phi)\geq 0$ in Ω1 and
$-\Delta(\varphi-\phi)+Q(\varphi-\phi)\geq 0$ in Ω1 and ![]() $\varphi-\phi=0$ on
$\varphi-\phi=0$ on ![]() $\partial\Omega_1$. Thus,
$\partial\Omega_1$. Thus, ![]() $\varphi\geq\phi$ in Ω1, which is a contradiction. Therefore,
$\varphi\geq\phi$ in Ω1, which is a contradiction. Therefore, ![]() $\Omega_1=\emptyset$, and the lemma is proved.
$\Omega_1=\emptyset$, and the lemma is proved.
Remark 2.2. Let Ω be a ![]() $C^{1,1}$ bounded domain and
$C^{1,1}$ bounded domain and ![]() $m\in L^\infty(\Omega)$ with
$m\in L^\infty(\Omega)$ with ![]() $m^+(x)\not\equiv 0$ in Ω. From [Reference Hess and Kato33], we can define
$m^+(x)\not\equiv 0$ in Ω. From [Reference Hess and Kato33], we can define ![]() $\lambda_{1m}(\Omega)$ and
$\lambda_{1m}(\Omega)$ and ![]() $\varphi_{1m\Omega}$ respectively as the principal eigenvalue and first eigenfunction to the problem
$\varphi_{1m\Omega}$ respectively as the principal eigenvalue and first eigenfunction to the problem
 \begin{equation*}
\left\{
\begin{array}{lll}
-\Delta\varphi=\lambda m(x)\varphi&,x\in\Omega
\\
\varphi=0&,x\in\partial\Omega.
\end{array}
\right.
\end{equation*}
\begin{equation*}
\left\{
\begin{array}{lll}
-\Delta\varphi=\lambda m(x)\varphi&,x\in\Omega
\\
\varphi=0&,x\in\partial\Omega.
\end{array}
\right.
\end{equation*}Moreover,
 \begin{equation*}
0 \lt \dfrac{1}{\lambda_{1m}(\Omega)}=\sup_{w\in H_0^1(\Omega)}\frac{\int_{\Omega}m(x)w^2\,\mathrm{d}x}{\int_{\Omega}|\nabla w|^2\,\mathrm{d}x}
\end{equation*}
\begin{equation*}
0 \lt \dfrac{1}{\lambda_{1m}(\Omega)}=\sup_{w\in H_0^1(\Omega)}\frac{\int_{\Omega}m(x)w^2\,\mathrm{d}x}{\int_{\Omega}|\nabla w|^2\,\mathrm{d}x}
\end{equation*} and ![]() $\varphi_{1m\Omega} \gt 0$ in Ω. Observe that by the standard regularity theory, we have
$\varphi_{1m\Omega} \gt 0$ in Ω. Observe that by the standard regularity theory, we have  $\varphi_{1m\Omega}\in W^{2,s}(\Omega)\cap W^{1,s}_0(\Omega)\cap C^1(\overline{\Omega})$ for s > 1.
$\varphi_{1m\Omega}\in W^{2,s}(\Omega)\cap W^{1,s}_0(\Omega)\cap C^1(\overline{\Omega})$ for s > 1.
In what follows, for the set ![]() $\Omega_0\subset\Omega$ and
$\Omega_0\subset\Omega$ and ![]() $m\in L^\infty(\Omega_0)$ with
$m\in L^\infty(\Omega_0)$ with ![]() $m^+(x)\not\equiv 0$ in Ω0, we will write
$m^+(x)\not\equiv 0$ in Ω0, we will write ![]() $\lambda_{1m}$ and
$\lambda_{1m}$ and ![]() $\varphi_{1m}$ instead of
$\varphi_{1m}$ instead of ![]() $\lambda_{1m\Omega_0}$ and
$\lambda_{1m\Omega_0}$ and ![]() $\varphi_{1m\Omega_0}$. We will also consider throughout this work that
$\varphi_{1m\Omega_0}$. We will also consider throughout this work that ![]() $\|\varphi_{1m}\|_\infty=1$.
$\|\varphi_{1m}\|_\infty=1$.
Corollary 2.3. Suppose that for some C 1 bounded domain ![]() $\Omega_0\subset\Omega$, we have
$\Omega_0\subset\Omega$, we have ![]() $-\Delta w\geq tm(x)w^r$ in Ω0, where
$-\Delta w\geq tm(x)w^r$ in Ω0, where ![]() $w\in W^{2,s}(\Omega)\cap C^1(\overline{\Omega})$, t > 0,
$w\in W^{2,s}(\Omega)\cap C^1(\overline{\Omega})$, t > 0, ![]() $0 \lt r \lt 1$,
$0 \lt r \lt 1$, ![]() $0\leq m(x)\not\equiv 0$,
$0\leq m(x)\not\equiv 0$, ![]() $x\in\Omega_0$, and w > 0 in Ω0. Then we have
$x\in\Omega_0$, and w > 0 in Ω0. Then we have
 \begin{equation*}
w(x)\geq \left(\dfrac{t}{\lambda_{1m}}\right)^{\frac{1}{1-r}}\varphi_{1m}(x),\,\,\,\,\,\forall x\in\Omega_0.
\end{equation*}
\begin{equation*}
w(x)\geq \left(\dfrac{t}{\lambda_{1m}}\right)^{\frac{1}{1-r}}\varphi_{1m}(x),\,\,\,\,\,\forall x\in\Omega_0.
\end{equation*}Proof. It is easy to verify that  $\overline{\varphi}_{1m}(x)=\left(\dfrac{t}{\lambda_{1m}}\right)^{\frac{1}{1-r}}\varphi_{1m}(x)$ satisfies
$\overline{\varphi}_{1m}(x)=\left(\dfrac{t}{\lambda_{1m}}\right)^{\frac{1}{1-r}}\varphi_{1m}(x)$ satisfies ![]() $-\Delta\overline{\varphi}_{1m}\leq tg(x)\overline{\varphi}_{1m}^r$, so the corollary is a direct consequence of Lemma 2.1.
$-\Delta\overline{\varphi}_{1m}\leq tg(x)\overline{\varphi}_{1m}^r$, so the corollary is a direct consequence of Lemma 2.1.
The following two propositions will provide sufficient conditions for systems ![]() ${(\mathcal{P}_1)}$ and
${(\mathcal{P}_1)}$ and ![]() ${(\mathcal{P}_2)}$ to have no solution, in the sense of Definition 1.1. In this section,
${(\mathcal{P}_2)}$ to have no solution, in the sense of Definition 1.1. In this section, ![]() ${\Omega \subset \mathbb{R}^N}$ is a bounded domain, and
${\Omega \subset \mathbb{R}^N}$ is a bounded domain, and ![]() ${\Omega_0 \subset \Omega}$ is a domain whose boundary will have regularity
${\Omega_0 \subset \Omega}$ is a domain whose boundary will have regularity ![]() ${C^1}$ or
${C^1}$ or ![]() ${C^{1,1}}$.
${C^{1,1}}$.
The only requirement we will impose on the signs of the weight functions is that they must satisfy condition ![]() $(P_{\Omega_0})$, where
$(P_{\Omega_0})$, where ![]() $\Omega_0\subset\Omega$. That is, these functions must be non-negative and non-zero in Ω0. Outside of Ω0, we are not imposing any specific behavior regarding the sign; in other words, the functions may or may not have an indefinite sign in Ω.
$\Omega_0\subset\Omega$. That is, these functions must be non-negative and non-zero in Ω0. Outside of Ω0, we are not imposing any specific behavior regarding the sign; in other words, the functions may or may not have an indefinite sign in Ω.
Proposition 2.4. Suppose that for some C 1 domain ![]() $\Omega_0\subset\Omega$, the weights
$\Omega_0\subset\Omega$, the weights ![]() $a(\cdot)$,
$a(\cdot)$, ![]() $b(\cdot)$,
$b(\cdot)$, ![]() $c(\cdot)$,
$c(\cdot)$, ![]() $d(\cdot)$ satisfy the condition
$d(\cdot)$ satisfy the condition ![]() $(P_{\Omega_0})$, and
$(P_{\Omega_0})$, and ![]() $\alpha\geq 1$, β, γ, θ > 0. Then there is a number
$\alpha\geq 1$, β, γ, θ > 0. Then there is a number ![]() $\Lambda^*_1 := \Lambda_1(a(\cdot),b(\cdot),c(\cdot),d(\cdot), p,q,\alpha,\beta) \gt 0$ such that:
$\Lambda^*_1 := \Lambda_1(a(\cdot),b(\cdot),c(\cdot),d(\cdot), p,q,\alpha,\beta) \gt 0$ such that:
(i) There are no solutions for
 $(\mathcal{P}_1)$ with
$(\mathcal{P}_1)$ with  $\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}} \gt \Lambda^*_1$;
$\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}} \gt \Lambda^*_1$;(ii) There are no solutions for
 $(\mathcal{P}_2)$ with
$(\mathcal{P}_2)$ with  $\lambda \gt \Lambda^*_1$.
$\lambda \gt \Lambda^*_1$.
Proof. In what follows we will consider ![]() $x\in\Omega_0$.
$x\in\Omega_0$.
Case (i): Since ![]() $-\Delta u\geq \lambda a(x)u^q$ and
$-\Delta u\geq \lambda a(x)u^q$ and ![]() $-\Delta v\geq \mu b(x)v^p$ by Corollary 2.3, we have
$-\Delta v\geq \mu b(x)v^p$ by Corollary 2.3, we have
 \begin{equation}
u\geq \left(\frac{\lambda}{\lambda_{1a}}\right)^{\frac{1}{1-q}}\varphi_{1a}
\,\,\,\,
\mbox{and}
\,\,\,\,
v\geq \left(\frac{\mu}{\lambda_{1b}}\right)^{\frac{1}{1-p}}\varphi_{1b}.
\end{equation}
\begin{equation}
u\geq \left(\frac{\lambda}{\lambda_{1a}}\right)^{\frac{1}{1-q}}\varphi_{1a}
\,\,\,\,
\mbox{and}
\,\,\,\,
v\geq \left(\frac{\mu}{\lambda_{1b}}\right)^{\frac{1}{1-p}}\varphi_{1b}.
\end{equation} Since ![]() $-\Delta u\geq c(x)u^\alpha v^\beta $ by Equation (2.1), we get
$-\Delta u\geq c(x)u^\alpha v^\beta $ by Equation (2.1), we get  $
-\Delta u\geq \lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}}\overline{c}(x)u$, where
$
-\Delta u\geq \lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}}\overline{c}(x)u$, where  $
\overline{c}(x):=\lambda_{1a}^{\frac{1-\alpha}{1-q}}\lambda_{1b}^{\frac{-\beta}{1-p}}
\varphi_{1a}^{\alpha-1}(x)\varphi_{1b}^\beta(x)c(x)
$ so
$
\overline{c}(x):=\lambda_{1a}^{\frac{1-\alpha}{1-q}}\lambda_{1b}^{\frac{-\beta}{1-p}}
\varphi_{1a}^{\alpha-1}(x)\varphi_{1b}^\beta(x)c(x)
$ so  $-\varphi_{1\overline{c}}\Delta u\geq \lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}}\overline{c}(x)\varphi_{1\overline{c}}u$, a simple computation provides
$-\varphi_{1\overline{c}}\Delta u\geq \lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}}\overline{c}(x)\varphi_{1\overline{c}}u$, a simple computation provides  $\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}}\leq \lambda_{1\overline{c}}$.
$\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}}\leq \lambda_{1\overline{c}}$.
Case (ii): In this case, we have  $u\geq \lambda_{1a}^{\frac{-1}{1-q}}\varphi_{1a}$ and
$u\geq \lambda_{1a}^{\frac{-1}{1-q}}\varphi_{1a}$ and  $v\geq \lambda_{1b}^{\frac{-1}{1-p}}\varphi_{1b}$, since
$v\geq \lambda_{1b}^{\frac{-1}{1-p}}\varphi_{1b}$, since ![]() $-\Delta u\geq \lambda c(x) u^\alpha v^\beta$ then
$-\Delta u\geq \lambda c(x) u^\alpha v^\beta$ then ![]() $-\Delta u\geq \lambda \overline{c}(x)u$, as in the last case we have
$-\Delta u\geq \lambda \overline{c}(x)u$, as in the last case we have ![]() $\lambda \leq \lambda_{1\overline{c}}$.
$\lambda \leq \lambda_{1\overline{c}}$.
Remark 2.5. Suppose that ![]() $(PW_1)$ holds, and
$(PW_1)$ holds, and ![]() $a(\cdot)$,
$a(\cdot)$, ![]() $b(\cdot)$,
$b(\cdot)$, ![]() $c(\cdot)$ and
$c(\cdot)$ and ![]() $d(\cdot)$ satisfy the
$d(\cdot)$ satisfy the ![]() $(P_{\Omega_0})$ condition,for some C 1 domain
$(P_{\Omega_0})$ condition,for some C 1 domain ![]() ${\Omega_0\subset\Omega}$. From Proposition 2.4, there are numbers
${\Omega_0\subset\Omega}$. From Proposition 2.4, there are numbers ![]() $\Lambda^*_i \gt 0$,
$\Lambda^*_i \gt 0$, ![]() $i=1,\,2$, such that:
$i=1,\,2$, such that:
(i) There is no solution (u, v) for
 $(\mathcal{P}_1)$ with
$(\mathcal{P}_1)$ with  $
\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}} \gt \Lambda^*_1
\,\,\,\,\mbox{or}\,\,\,\,
\mu^{\frac{\gamma-1}{1-p}}\lambda^{\frac{\theta}{1-q}} \gt \Lambda^*_2
$;
$
\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}} \gt \Lambda^*_1
\,\,\,\,\mbox{or}\,\,\,\,
\mu^{\frac{\gamma-1}{1-p}}\lambda^{\frac{\theta}{1-q}} \gt \Lambda^*_2
$;(ii) There is no solution (u, v) for
 $(\mathcal{P}_2)$ with
$(\mathcal{P}_2)$ with  $\lambda \gt \Lambda^*_1$ or
$\lambda \gt \Lambda^*_1$ or  $\mu \gt \Lambda^*_2$.
$\mu \gt \Lambda^*_2$.
Before we present the next non-existence theorem, we will present a version of the Krein–Rutman theorem [Reference Krein and Rutman37]. The proof of this result can be found in [Reference Rabinowitz40] or [Reference Brézis11, Problem 41, p. 499]. This theorem plays a crucial role in the proof of our non-existence theorem.
Theorem 2.6 (Krein–Rutman)
Let E be a Banach space and let P be a convex cone with vertex at 0, i.e. ![]() $\lambda u+\mu v\in P,\,\,\forall
\lambda,\,\mu\geq 0,\,\forall u,\,v\in P$. Assume that P is closed, Int
$\lambda u+\mu v\in P,\,\,\forall
\lambda,\,\mu\geq 0,\,\forall u,\,v\in P$. Assume that P is closed, Int![]() $P\neq\emptyset$ and P ≠ E. Let
$P\neq\emptyset$ and P ≠ E. Let ![]() $T:E\rightarrow E$ be a compact operator such that
$T:E\rightarrow E$ be a compact operator such that ![]() $T(P\setminus\{0\})\subset \mbox{Int}P$. Then there exists some
$T(P\setminus\{0\})\subset \mbox{Int}P$. Then there exists some ![]() $u_0\in {int}P$ and some
$u_0\in {int}P$ and some ![]() $\lambda_0 \gt 0$ such that
$\lambda_0 \gt 0$ such that ![]() $T u_0 = \lambda_0 u_0$.
$T u_0 = \lambda_0 u_0$.
Proposition 2.7. Suppose that ![]() $(PW_2)$ holds, and for some
$(PW_2)$ holds, and for some ![]() $C^{1,1}$ bounded domain
$C^{1,1}$ bounded domain ![]() $\Omega_0\subset\Omega$, the weights
$\Omega_0\subset\Omega$, the weights ![]() $a(\cdot),b(\cdot),c(\cdot), d(\cdot)$ satisfy the
$a(\cdot),b(\cdot),c(\cdot), d(\cdot)$ satisfy the ![]() $(P_{\Omega_0})$ condition. Then there are positive numbers
$(P_{\Omega_0})$ condition. Then there are positive numbers ![]() $\Lambda^*_i:=\Lambda^*_i(a(\cdot),b(\cdot),c(\cdot),d(\cdot),p,q,\alpha,\beta,\theta,\gamma)$ such that:
$\Lambda^*_i:=\Lambda^*_i(a(\cdot),b(\cdot),c(\cdot),d(\cdot),p,q,\alpha,\beta,\theta,\gamma)$ such that:
(i) There is no solution (u, v) for
 $(\mathcal{P}_1)$, in the sense of Definition 1.1, with
$(\mathcal{P}_1)$, in the sense of Definition 1.1, with  $u(x),v(x) \gt 0,\,\,\forall x\in\Omega_0$, and
$u(x),v(x) \gt 0,\,\,\forall x\in\Omega_0$, and  $\lambda \gt \Lambda_1^*$ or
$\lambda \gt \Lambda_1^*$ or  $\mu \gt \Lambda^*_2$;
$\mu \gt \Lambda^*_2$;(ii) There is no solution (u, v) for
 $(\mathcal{P}_2)$, in the sense of Definition 1.1, with
$(\mathcal{P}_2)$, in the sense of Definition 1.1, with  $u(x),v(x) \gt 0,\,\,\forall x\in\Omega_0$, and
$u(x),v(x) \gt 0,\,\,\forall x\in\Omega_0$, and  $\lambda^{1-\gamma}\mu^{\beta} \gt \Lambda^*_3$ or
$\lambda^{1-\gamma}\mu^{\beta} \gt \Lambda^*_3$ or  $\lambda^\theta\mu^{1-\alpha} \gt \Lambda^*_4$.
$\lambda^\theta\mu^{1-\alpha} \gt \Lambda^*_4$.
Proof. In what follows, we will consider ![]() $x\in\Omega_0$.
$x\in\Omega_0$.
Case (i): Suppose that (u, v) is a solution for ![]() $(\mathcal{P}_1)$ with
$(\mathcal{P}_1)$ with ![]() $u(x),v(x) \gt 0,\,\,\forall x\in\Omega_0$. From Corollary 2.3, we have
$u(x),v(x) \gt 0,\,\,\forall x\in\Omega_0$. From Corollary 2.3, we have
 \begin{equation}
u\geq \left(\frac{\lambda}{\lambda_{1a}}\right)^{\frac{1}{1-q}}\varphi_{1a}.
\end{equation}
\begin{equation}
u\geq \left(\frac{\lambda}{\lambda_{1a}}\right)^{\frac{1}{1-q}}\varphi_{1a}.
\end{equation} Since ![]() $-\Delta v\geq d(x)u^\theta v^\gamma$ by Equation (2.2), we get
$-\Delta v\geq d(x)u^\theta v^\gamma$ by Equation (2.2), we get
 \begin{equation*}
-\Delta v\geq \lambda^{\frac{\theta}{1-q}} \sigma(x) v^\gamma
\end{equation*}
\begin{equation*}
-\Delta v\geq \lambda^{\frac{\theta}{1-q}} \sigma(x) v^\gamma
\end{equation*} where  $\sigma(x):=\lambda_{1a}^{\frac{-\theta}{1-q}} d(x)\varphi^\theta_{1a}(x)$. Since
$\sigma(x):=\lambda_{1a}^{\frac{-\theta}{1-q}} d(x)\varphi^\theta_{1a}(x)$. Since ![]() $0 \lt \gamma \lt 1$, from Corollary 2.3, we obtain
$0 \lt \gamma \lt 1$, from Corollary 2.3, we obtain
 \begin{equation}
v(x)\geq \lambda^{\frac{\theta}{(1-q)(1-\gamma)}}\lambda_{1\sigma}^{\frac{-1}{1-\gamma}} \varphi_{1\sigma}(x).
\end{equation}
\begin{equation}
v(x)\geq \lambda^{\frac{\theta}{(1-q)(1-\gamma)}}\lambda_{1\sigma}^{\frac{-1}{1-\gamma}} \varphi_{1\sigma}(x).
\end{equation} Since ![]() $-\Delta u\geq c(x)u^\alpha v^\beta$, Equations (2.2) and (2.3) provide
$-\Delta u\geq c(x)u^\alpha v^\beta$, Equations (2.2) and (2.3) provide
where  $\sigma_1(x)=\lambda_{1a}^{\frac{-\alpha}{1-q}} \lambda_{1\sigma}^{\frac{-(\beta-1)}{1-\gamma}} c(x)\varphi_{1a}^\alpha(x)\varphi_{1\sigma}^{\beta-1}(x)$ and
$\sigma_1(x)=\lambda_{1a}^{\frac{-\alpha}{1-q}} \lambda_{1\sigma}^{\frac{-(\beta-1)}{1-\gamma}} c(x)\varphi_{1a}^\alpha(x)\varphi_{1\sigma}^{\beta-1}(x)$ and  $\tau_1=\frac{\alpha}{1-q}+\frac{\theta(\beta-1)}{(1-q)(1-\gamma)}$. Once again using
$\tau_1=\frac{\alpha}{1-q}+\frac{\theta(\beta-1)}{(1-q)(1-\gamma)}$. Once again using ![]() $-\Delta v\geq d(x)u^\theta v^\gamma$ with Equations (2.2) and (2.3), we get
$-\Delta v\geq d(x)u^\theta v^\gamma$ with Equations (2.2) and (2.3), we get
where  $\sigma_2(x)=\lambda_{1a}^{\frac{1-\theta}{q-1}}\lambda_{1\sigma}^{\frac{-\gamma}{1-\gamma}} d(x)\varphi_{1\sigma}^\gamma(x)\varphi_{1a}^{\theta-1}(x)$ and
$\sigma_2(x)=\lambda_{1a}^{\frac{1-\theta}{q-1}}\lambda_{1\sigma}^{\frac{-\gamma}{1-\gamma}} d(x)\varphi_{1\sigma}^\gamma(x)\varphi_{1a}^{\theta-1}(x)$ and  $\tau_2=\frac{\theta-1}{1-q}+\frac{\theta\gamma}{(1-q)(1-\gamma)}.$
$\tau_2=\frac{\theta-1}{1-q}+\frac{\theta\gamma}{(1-q)(1-\gamma)}.$
Claim: There is a principal eigenvalue ![]() $\lambda_{12} \gt 0$ and principal eigenfunctions
$\lambda_{12} \gt 0$ and principal eigenfunctions ![]() $\phi_1,\,\,\phi_2 \gt 0,\,\,\forall x\in\Omega_0$ belonging to
$\phi_1,\,\,\phi_2 \gt 0,\,\,\forall x\in\Omega_0$ belonging to  $W^{2,s}(\Omega)\cap W_0^{1,s}(\Omega_0)\cap C^1(\overline{\Omega}_0),\,\,\forall s \gt 1$ for the problem:
$W^{2,s}(\Omega)\cap W_0^{1,s}(\Omega_0)\cap C^1(\overline{\Omega}_0),\,\,\forall s \gt 1$ for the problem:
 \begin{align}
\left\{
\begin{array}{rlc}
-\Delta\phi_1&=&\lambda_{12}\sigma_1(x)\phi_2,\,\,\Omega_0
\\
-\Delta\phi_2&=&\lambda_{12}\sigma_2(x)\phi_1,\,\,\Omega_0.
\end{array}
\right.
\end{align}
\begin{align}
\left\{
\begin{array}{rlc}
-\Delta\phi_1&=&\lambda_{12}\sigma_1(x)\phi_2,\,\,\Omega_0
\\
-\Delta\phi_2&=&\lambda_{12}\sigma_2(x)\phi_1,\,\,\Omega_0.
\end{array}
\right.
\end{align}From Equation (2.4), we get
 \begin{equation*}
\lambda_{12}\int_{\Omega_0}\sigma_2(x)u\phi_1\,\mathrm{d}x=
\int_{\Omega_0}-u\Delta\phi_2\,\mathrm{d}x\geq -\int_{\Omega_0}\phi_2\Delta u\,\mathrm{d}x\geq \lambda^{\tau_1}\int_{\Omega_0}\sigma_1(x)v\phi_2\,\mathrm{d}x.
\end{equation*}
\begin{equation*}
\lambda_{12}\int_{\Omega_0}\sigma_2(x)u\phi_1\,\mathrm{d}x=
\int_{\Omega_0}-u\Delta\phi_2\,\mathrm{d}x\geq -\int_{\Omega_0}\phi_2\Delta u\,\mathrm{d}x\geq \lambda^{\tau_1}\int_{\Omega_0}\sigma_1(x)v\phi_2\,\mathrm{d}x.
\end{equation*}Therefore,
 \begin{equation}
\lambda_{12}\int_{\Omega_0}\sigma_2(x)u\phi_1\,\mathrm{d}x\geq \lambda^{\tau_1}
\int_{\Omega_0}\sigma_1(x)v\phi_2\,\mathrm{d}x.
\end{equation}
\begin{equation}
\lambda_{12}\int_{\Omega_0}\sigma_2(x)u\phi_1\,\mathrm{d}x\geq \lambda^{\tau_1}
\int_{\Omega_0}\sigma_1(x)v\phi_2\,\mathrm{d}x.
\end{equation}Similarly, we get
 \begin{equation}
\lambda_{12}\int_{\Omega_0}\sigma_1(x)v\phi_2\,\mathrm{d}x\geq \lambda^{\tau_2}
\int_{\Omega_0}\sigma_2(x)u\phi_1\,\mathrm{d}x.
\end{equation}
\begin{equation}
\lambda_{12}\int_{\Omega_0}\sigma_1(x)v\phi_2\,\mathrm{d}x\geq \lambda^{\tau_2}
\int_{\Omega_0}\sigma_2(x)u\phi_1\,\mathrm{d}x.
\end{equation} Follows from Equations (2.6) and (2.7) that ![]() $\lambda^{\tau_1+\tau_2}\leq \lambda_{12}^2$, so it is enough to consider
$\lambda^{\tau_1+\tau_2}\leq \lambda_{12}^2$, so it is enough to consider  $\Lambda^*_1=\lambda_{12}^{\frac{2}{\tau_1+\tau_2}}$. Now we will prove the Claim. Let
$\Lambda^*_1=\lambda_{12}^{\frac{2}{\tau_1+\tau_2}}$. Now we will prove the Claim. Let ![]() $E=C^1(\overline{\Omega}_0)\cap H_0^1(\Omega_0)$ and
$E=C^1(\overline{\Omega}_0)\cap H_0^1(\Omega_0)$ and ![]() $P=\{u\in E\,\,|\,\,u(x)\geq 0,\,x\in\Omega_0\}$. It is known that
$P=\{u\in E\,\,|\,\,u(x)\geq 0,\,x\in\Omega_0\}$. It is known that
 \begin{equation*}
\text{int } P=\left\{u\in E\,\,|\,\,u(x) \gt 0,\,x\in\Omega_0,\,\,\frac{\partial u}{\partial
\nu} \lt 0,\,x\in\partial\Omega_0\right\}.
\end{equation*}
\begin{equation*}
\text{int } P=\left\{u\in E\,\,|\,\,u(x) \gt 0,\,x\in\Omega_0,\,\,\frac{\partial u}{\partial
\nu} \lt 0,\,x\in\partial\Omega_0\right\}.
\end{equation*} For ![]() $i=1,2$, we set the operators
$i=1,2$, we set the operators ![]() $T_i:E\rightarrow E$ by
$T_i:E\rightarrow E$ by ![]() $T_i(u)=v$, where
$T_i(u)=v$, where  $v\in W^{2,s}(\Omega_0)\cap W^{1,s}_0(\Omega_0)\cap C^1(\overline{\Omega_0})$ is the unique solution of the problem
$v\in W^{2,s}(\Omega_0)\cap W^{1,s}_0(\Omega_0)\cap C^1(\overline{\Omega_0})$ is the unique solution of the problem
from [Reference Gilbarg and Trudinger31, Theorems 7.26, 9.15 and Lemma 9.17], we have that ![]() ${T_i}$ is well-defined and
${T_i}$ is well-defined and ![]() ${T:=T_2\circ T_1}$ is a compact operator. Moreover, utilizing the maximum principles [Reference Gilbarg and Trudinger31, Theorems 8.1 and 8.19] along with Hopf’s lemma [Reference Hopf35] (see also [Reference Gilbarg and Trudinger31, Lemma 3.4] and Remark 2.8), we have
${T:=T_2\circ T_1}$ is a compact operator. Moreover, utilizing the maximum principles [Reference Gilbarg and Trudinger31, Theorems 8.1 and 8.19] along with Hopf’s lemma [Reference Hopf35] (see also [Reference Gilbarg and Trudinger31, Lemma 3.4] and Remark 2.8), we have ![]() $T(P\setminus\{0\})\subset \text{int }P$; therefore, Theorem 2.6 provides
$T(P\setminus\{0\})\subset \text{int }P$; therefore, Theorem 2.6 provides ![]() $u_0\in \text{int }P$ and
$u_0\in \text{int }P$ and ![]() $\lambda_0 \gt 0$ such that
$\lambda_0 \gt 0$ such that ![]() $Tu_0=\lambda_0u_0$, hence
$Tu_0=\lambda_0u_0$, hence  $\lambda_{12}=\lambda_0^{-1/2}$,
$\lambda_{12}=\lambda_0^{-1/2}$,  $\phi_1=\lambda_0^{-1/2}T_1u_0$ and
$\phi_1=\lambda_0^{-1/2}T_1u_0$ and ![]() $\phi_2=u_0$ are solutions for
$\phi_2=u_0$ are solutions for ![]() $(\mathcal{LP})$. In a similar way, we prove that for some
$(\mathcal{LP})$. In a similar way, we prove that for some ![]() $\Lambda^*_2$, there are no solutions for
$\Lambda^*_2$, there are no solutions for ![]() $\mu \gt \Lambda^*_2$.
$\mu \gt \Lambda^*_2$.
Case (ii): In what follows, we consider ![]() $x\in\Omega_0$. Suppose that (u, v) is a solution for
$x\in\Omega_0$. Suppose that (u, v) is a solution for ![]() $(\mathcal{P}_2)$. Since
$(\mathcal{P}_2)$. Since ![]() $-\Delta u\geq a(x)u^q$ and
$-\Delta u\geq a(x)u^q$ and ![]() $-\Delta v\geq b(x)v^p$, we have
$-\Delta v\geq b(x)v^p$, we have
 \begin{equation}
u\geq \lambda^{\frac{-1}{1-q}}_{1a}\varphi_{1a}
\,\,\,\,\,\mbox{and}\,\,\,\,\,
v\geq \lambda^{\frac{-1}{1-p}}_{1b}\varphi_{1b}.
\end{equation}
\begin{equation}
u\geq \lambda^{\frac{-1}{1-q}}_{1a}\varphi_{1a}
\,\,\,\,\,\mbox{and}\,\,\,\,\,
v\geq \lambda^{\frac{-1}{1-p}}_{1b}\varphi_{1b}.
\end{equation} Since ![]() $-\Delta u\geq \lambda c(x)u^\alpha v^\beta$ and
$-\Delta u\geq \lambda c(x)u^\alpha v^\beta$ and ![]() $-\Delta v\geq \mu d(x)u^\theta v^\gamma$, we have
$-\Delta v\geq \mu d(x)u^\theta v^\gamma$, we have
where  $\sigma(x)=\lambda_{1b}^{\frac{-\beta}{1-p}}c(x)\varphi_{1b}^\beta(x)$ and
$\sigma(x)=\lambda_{1b}^{\frac{-\beta}{1-p}}c(x)\varphi_{1b}^\beta(x)$ and  $\overline{\sigma}(x)=\lambda_{1a}^{\frac{-\theta}{1-q}}d(x)\varphi_{1a}^\theta(x)$. By Equation (2.9), we get
$\overline{\sigma}(x)=\lambda_{1a}^{\frac{-\theta}{1-q}}d(x)\varphi_{1a}^\theta(x)$. By Equation (2.9), we get
 \begin{equation}
u\geq \left(\frac{\lambda}{\lambda_{1\sigma}}\right)^{\frac{1}{1-\alpha}}\varphi_{1\sigma}
\,\,\,\,\,\mbox{and}\,\,\,\,\,
v\geq \left(\frac{\mu}{\lambda_{1\overline{\sigma}}}\right)^{\frac{1}{1-\gamma}}\varphi_{1
\overline{\sigma}}.
\end{equation}
\begin{equation}
u\geq \left(\frac{\lambda}{\lambda_{1\sigma}}\right)^{\frac{1}{1-\alpha}}\varphi_{1\sigma}
\,\,\,\,\,\mbox{and}\,\,\,\,\,
v\geq \left(\frac{\mu}{\lambda_{1\overline{\sigma}}}\right)^{\frac{1}{1-\gamma}}\varphi_{1
\overline{\sigma}}.
\end{equation} From Equations (2.8) and (2.10), ![]() $-\Delta u\geq \lambda c(x)u^\alpha v^\beta$ and
$-\Delta u\geq \lambda c(x)u^\alpha v^\beta$ and ![]() $-\Delta v\geq \mu d(x)u^\theta v^\gamma$, we obtain
$-\Delta v\geq \mu d(x)u^\theta v^\gamma$, we obtain
 \begin{equation}
\left\{
\begin{array}{lcl}
-\Delta u\geq \lambda^{\frac{1}{1-\alpha}}\overline{c}(x) v
\\
-\Delta v\geq \lambda^{\frac{\theta-1}{1-\alpha}}\mu\overline{d}(x) u
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{lcl}
-\Delta u\geq \lambda^{\frac{1}{1-\alpha}}\overline{c}(x) v
\\
-\Delta v\geq \lambda^{\frac{\theta-1}{1-\alpha}}\mu\overline{d}(x) u
\end{array}
\right.
\end{equation} where  $\overline{c}(x)=\lambda_{1\sigma}^{\frac{-\alpha}{1-\alpha}}
\lambda_{1b}^{\frac{1-\beta}{1-p}}\varphi_{1\sigma}^\alpha(x)\varphi_{1b}^{\beta-1}(x)c(x)$ and
$\overline{c}(x)=\lambda_{1\sigma}^{\frac{-\alpha}{1-\alpha}}
\lambda_{1b}^{\frac{1-\beta}{1-p}}\varphi_{1\sigma}^\alpha(x)\varphi_{1b}^{\beta-1}(x)c(x)$ and  $\overline{d}(x)=\lambda_{1\sigma}^{\frac{1-\theta}{1-\alpha}}
\lambda_{1b}^{\frac{-\gamma}{1-p}}\sigma_{1\sigma}^{\theta-1}(x)\varphi_{1b}^\gamma(x)d(x)
$. From Equation (2.11), we can proceed as in the proof of Case (i) to obtain
$\overline{d}(x)=\lambda_{1\sigma}^{\frac{1-\theta}{1-\alpha}}
\lambda_{1b}^{\frac{-\gamma}{1-p}}\sigma_{1\sigma}^{\theta-1}(x)\varphi_{1b}^\gamma(x)d(x)
$. From Equation (2.11), we can proceed as in the proof of Case (i) to obtain ![]() $\Lambda_3^*$ such that
$\Lambda_3^*$ such that
 \begin{equation*}
(\Lambda_3^*)^{\frac{1}{1-\alpha}}\geq\lambda^{\frac{1}{1-\alpha}}\lambda^{\frac{\theta-1}{1-\alpha}}\mu
=\lambda^{\frac{\theta}{1-\alpha}}\mu\,\,\,\Longrightarrow\,\,\, \Lambda_3^*\geq\lambda^\theta\mu^{1-\alpha}.
\end{equation*}
\begin{equation*}
(\Lambda_3^*)^{\frac{1}{1-\alpha}}\geq\lambda^{\frac{1}{1-\alpha}}\lambda^{\frac{\theta-1}{1-\alpha}}\mu
=\lambda^{\frac{\theta}{1-\alpha}}\mu\,\,\,\Longrightarrow\,\,\, \Lambda_3^*\geq\lambda^\theta\mu^{1-\alpha}.
\end{equation*}In a similar way, we get ![]() $\Lambda^*_4 \gt 0$ such that
$\Lambda^*_4 \gt 0$ such that ![]() $\Lambda_4^*\geq \lambda^{1-\gamma}\mu^\beta$.
$\Lambda_4^*\geq \lambda^{1-\gamma}\mu^\beta$.
Remark 2.8. Traditionally, the Hopf Lemma [Reference Hopf35] is presented for functions of class C 2. However, this result can be easily extended to functions in ![]() $W^{2,s}(\Omega)\cap C^1(\overline{\Omega})$ with
$W^{2,s}(\Omega)\cap C^1(\overline{\Omega})$ with ![]() $\partial\Omega\in C^{1,1}$. Indeed, although the proof given in [Reference Gilbarg and Trudinger31, Lemma 3.4] is for functions in
$\partial\Omega\in C^{1,1}$. Indeed, although the proof given in [Reference Gilbarg and Trudinger31, Lemma 3.4] is for functions in ![]() $C^2(\Omega)$, it essentially employs comparison principles for functions in
$C^2(\Omega)$, it essentially employs comparison principles for functions in ![]() $C^2(\Omega)\cap C^0(\overline{\Omega})$. Since
$C^2(\Omega)\cap C^0(\overline{\Omega})$. Since ![]() $\partial\Omega\in C^{1,1}$, Ω satisfies the interior sphere condition, ensuring that the proof of this result remains unchanged if we use the comparison principles for functions in
$\partial\Omega\in C^{1,1}$, Ω satisfies the interior sphere condition, ensuring that the proof of this result remains unchanged if we use the comparison principles for functions in ![]() $W^{1,2}(\Omega)$ (see [Reference Gilbarg and Trudinger31, Theorems 8.1 and 8.19], and also [Reference Gilbarg and Trudinger31, Sections 9.7–9.9] for maximum principles for functions in
$W^{1,2}(\Omega)$ (see [Reference Gilbarg and Trudinger31, Theorems 8.1 and 8.19], and also [Reference Gilbarg and Trudinger31, Sections 9.7–9.9] for maximum principles for functions in ![]() $W^{2,N}(\Omega)$).
$W^{2,N}(\Omega)$).
Following the same idea of Proposition 2.4, part (i), and Proposition 2.7, part (ii), we have
Corollary 2.9. Suppose that ![]() $a(\cdot),\,b(\cdot),\,c(\cdot),\,d(\cdot)$ satisfy the
$a(\cdot),\,b(\cdot),\,c(\cdot),\,d(\cdot)$ satisfy the ![]() $(P_{\Omega_0})$ condition for some
$(P_{\Omega_0})$ condition for some ![]() ${C^{1,1}}$ domain
${C^{1,1}}$ domain ![]() ${\Omega_0 \subset \Omega}$, and
${\Omega_0 \subset \Omega}$, and ![]() $(PW_3)$ holds. Then there are
$(PW_3)$ holds. Then there are ![]() $\Lambda_i^* \gt 0$,
$\Lambda_i^* \gt 0$, ![]() $i = 1, 2, 3, 4$, satisfying:
$i = 1, 2, 3, 4$, satisfying:
(i) There is no solution (u, v) for
 $(\mathcal{P}_1)$ with
$(\mathcal{P}_1)$ with  $\lambda \gt \Lambda_1^*$ or
$\lambda \gt \Lambda_1^*$ or  $\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}} \gt \Lambda^*_2$;
$\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}} \gt \Lambda^*_2$;(ii) There is no solution (u, v) for
 $(\mathcal{P}_2)$ with
$(\mathcal{P}_2)$ with  $\lambda \gt \Lambda_3^*$ or
$\lambda \gt \Lambda_3^*$ or  $\lambda^{1-\gamma}\mu^\beta \gt \Lambda^*_4$.
$\lambda^{1-\gamma}\mu^\beta \gt \Lambda^*_4$.
3. The sub-supersolution method
In this section, we write ![]() $\phi^\pm(x):=\max\{0,\pm \phi(x)\}$ and
$\phi^\pm(x):=\max\{0,\pm \phi(x)\}$ and ![]() $\|\phi\|_\infty:=|\phi|_{L^\infty(\Omega)}$. We always assume that
$\|\phi\|_\infty:=|\phi|_{L^\infty(\Omega)}$. We always assume that ![]() ${\Omega \subset \mathbb{R}^N}$ is a bounded domain with
${\Omega \subset \mathbb{R}^N}$ is a bounded domain with ![]() ${\partial \Omega \in C^{1,1}}$. The following notation is of fundamental importance for the definition of sub and super-solutions: If
${\partial \Omega \in C^{1,1}}$. The following notation is of fundamental importance for the definition of sub and super-solutions: If ![]() $\phi\in L^\infty(\Omega)$, we set
$\phi\in L^\infty(\Omega)$, we set
We define ![]() ${(\overline{u}, \overline{v})}$ as a supersolution for
${(\overline{u}, \overline{v})}$ as a supersolution for ![]() ${(\mathcal{P}_i)}$ if, for all s > 1,
${(\mathcal{P}_i)}$ if, for all s > 1, ![]() $\overline{u}, \overline{v} \in W^{2,s}(\Omega) \cap$
$\overline{u}, \overline{v} \in W^{2,s}(\Omega) \cap$  $W_0^{1,s}(\Omega) \cap C^1(\overline{\Omega})$, and
$W_0^{1,s}(\Omega) \cap C^1(\overline{\Omega})$, and ![]() ${\overline{u}, \overline{v}}$ satisfy:
${\overline{u}, \overline{v}}$ satisfy:
 \begin{align}
\left\{
\begin{array}{ll}
-\Delta \overline{u}\geq f_\lambda(x,z,w)& \mbox{in}~~\Omega,\,\,\,\, \forall z\in[0,\overline{u}],\,\,\forall w\in[0,\overline{v}]
\\
-\Delta \overline{v}\geq g_\mu(x,z,w) &\mbox{in}~~\Omega,\,\,\,\,\forall z\in[0,\overline{u}],\,\,\forall w\in[0,\overline{v}]
\\
\overline{u},\,\,\overline{v} \gt 0& \mbox{in}~~\Omega
\\
\overline{u}=\overline{v}=0&\mbox{on}~~\partial\Omega
\end{array}
\right.
\end{align}
\begin{align}
\left\{
\begin{array}{ll}
-\Delta \overline{u}\geq f_\lambda(x,z,w)& \mbox{in}~~\Omega,\,\,\,\, \forall z\in[0,\overline{u}],\,\,\forall w\in[0,\overline{v}]
\\
-\Delta \overline{v}\geq g_\mu(x,z,w) &\mbox{in}~~\Omega,\,\,\,\,\forall z\in[0,\overline{u}],\,\,\forall w\in[0,\overline{v}]
\\
\overline{u},\,\,\overline{v} \gt 0& \mbox{in}~~\Omega
\\
\overline{u}=\overline{v}=0&\mbox{on}~~\partial\Omega
\end{array}
\right.
\end{align}where ![]() $f_\lambda(x,z,w)=\lambda a(x)z^q+c(x)z^\alpha w^\beta$ and
$f_\lambda(x,z,w)=\lambda a(x)z^q+c(x)z^\alpha w^\beta$ and ![]() $g_\mu(x,z,w)=\mu b(x)w^p+d(x)z^\theta w^\gamma$ for
$g_\mu(x,z,w)=\mu b(x)w^p+d(x)z^\theta w^\gamma$ for ![]() $(\mathcal{P}_1)$, and
$(\mathcal{P}_1)$, and ![]() $f_\lambda(x,z,w)=a(x)z^q+\lambda c(x)z^\alpha w^\beta$ and
$f_\lambda(x,z,w)=a(x)z^q+\lambda c(x)z^\alpha w^\beta$ and ![]() $g_\mu(x,z,w)=b(x)w^p+\mu d(x)z^\theta w^\gamma$ for
$g_\mu(x,z,w)=b(x)w^p+\mu d(x)z^\theta w^\gamma$ for ![]() $(\mathcal{P}_2)$.
$(\mathcal{P}_2)$.
Remark 3.1. When all weight functions ![]() $a,b,c,d\in L^\infty(\Omega)$ are non-negative, then a solution (u, v) to
$a,b,c,d\in L^\infty(\Omega)$ are non-negative, then a solution (u, v) to ![]() $(\mathcal{P}_i)$ with
$(\mathcal{P}_i)$ with ![]() $\lambda,\mu \gt 0$ is also a super-solution satisfying
$\lambda,\mu \gt 0$ is also a super-solution satisfying ![]() $(\overline{\mathcal{S}} _{\lambda\mu})$. However, if at least one of the weight functions changes sign in Ω or is negative on a set of positive measure, then a solution (u, v) to
$(\overline{\mathcal{S}} _{\lambda\mu})$. However, if at least one of the weight functions changes sign in Ω or is negative on a set of positive measure, then a solution (u, v) to ![]() $(\mathcal{P}_i)$ may not be a super-solution satisfying
$(\mathcal{P}_i)$ may not be a super-solution satisfying ![]() $(\overline{\mathcal{S}}_{\lambda\mu})$. This is a very relevant difference for the concept of super-solutions for systems, since in the scalar case, a solution is always a super-solution.
$(\overline{\mathcal{S}}_{\lambda\mu})$. This is a very relevant difference for the concept of super-solutions for systems, since in the scalar case, a solution is always a super-solution.
In the scalar case ![]() $(\mathcal{P}_\lambda)$ with
$(\mathcal{P}_\lambda)$ with ![]() $a\equiv b\equiv 1$, the authors of [Reference Ambrosetti, Brézis and Cerami4] obtained the first solution via the method of sub-super solutions. The super-solution for
$a\equiv b\equiv 1$, the authors of [Reference Ambrosetti, Brézis and Cerami4] obtained the first solution via the method of sub-super solutions. The super-solution for ![]() $(\mathcal{P}_\lambda)$ provided by these authors takes the form Me, where
$(\mathcal{P}_\lambda)$ provided by these authors takes the form Me, where ![]() $e\in C^2(\Omega)\cap C(\overline{\Omega})$ satisfies
$e\in C^2(\Omega)\cap C(\overline{\Omega})$ satisfies ![]() $-\Delta e=1$ in Ω and e = 0 on
$-\Delta e=1$ in Ω and e = 0 on ![]() $\partial\Omega$. For this super-solution to exist, it is sufficient that the inequality
$\partial\Omega$. For this super-solution to exist, it is sufficient that the inequality ![]() $M\geq \lambda M^q\|e\|^q_\infty+M^p\|e\|^p_\infty$ admits a solution
$M\geq \lambda M^q\|e\|^q_\infty+M^p\|e\|^p_\infty$ admits a solution ![]() $M=M(\lambda) \gt 0$ (see [Reference Ambrosetti, Brézis and Cerami4, Lemma 3.1]). In our approach, the super-solutions take the form
$M=M(\lambda) \gt 0$ (see [Reference Ambrosetti, Brézis and Cerami4, Lemma 3.1]). In our approach, the super-solutions take the form ![]() $\overline{u}=Xe$ and
$\overline{u}=Xe$ and ![]() $\overline{v}=Ye$, where
$\overline{v}=Ye$, where ![]() $X=X(\lambda,\mu) \gt 0$ and
$X=X(\lambda,\mu) \gt 0$ and ![]() $Y=Y(\lambda,\mu) \gt 0$ are real numbers, which depending on
$Y=Y(\lambda,\mu) \gt 0$ are real numbers, which depending on ![]() $(\mathcal{P}_1)$ or
$(\mathcal{P}_1)$ or ![]() $(\mathcal{P}_2)$, satisfy one of the following systems:
$(\mathcal{P}_2)$, satisfy one of the following systems:
 \begin{equation}
\left\{
\begin{array}{lcl}
X&\geq& \lambda AX^q+CX^\alpha Y^\beta
\\
Y&\geq& \mu BY^p+DX^\theta Y^\gamma
\\
&&X \gt 0,\,\,Y \gt 0
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{lcl}
X&\geq& \lambda AX^q+CX^\alpha Y^\beta
\\
Y&\geq& \mu BY^p+DX^\theta Y^\gamma
\\
&&X \gt 0,\,\,Y \gt 0
\end{array}
\right.
\end{equation} \begin{equation}
\left\{
\begin{array}{lcl}
X&\geq& AX^q+ \lambda CX^\alpha Y^\beta
\\
Y&\geq& BY^p+ \mu DX^\theta Y^\gamma
\\
&&X \gt 0,\,\,Y \gt 0,
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{lcl}
X&\geq& AX^q+ \lambda CX^\alpha Y^\beta
\\
Y&\geq& BY^p+ \mu DX^\theta Y^\gamma
\\
&&X \gt 0,\,\,Y \gt 0,
\end{array}
\right.
\end{equation} where ![]() $A,B,C,D\in \mathbb{R}$,
$A,B,C,D\in \mathbb{R}$, ![]() $p,q\in(0,1)$,
$p,q\in(0,1)$, ![]() $\alpha,\beta,\gamma,\theta \gt 0$,
$\alpha,\beta,\gamma,\theta \gt 0$, ![]() $\max\{\alpha,\beta\} \gt 1$ and
$\max\{\alpha,\beta\} \gt 1$ and ![]() $\max\{\gamma,\theta\} \gt 1$. For which values of λ > 0 and µ > 0 do the systems (3.1) and (3.2) have a solution (X, Y)? In Lemma 3.3, we will delve into this question; however, it should be noted that systems (3.1) and (3.2) always have a solution when λ > 0 and µ > 0 are sufficiently small. We will register this fact in a brief remark.
$\max\{\gamma,\theta\} \gt 1$. For which values of λ > 0 and µ > 0 do the systems (3.1) and (3.2) have a solution (X, Y)? In Lemma 3.3, we will delve into this question; however, it should be noted that systems (3.1) and (3.2) always have a solution when λ > 0 and µ > 0 are sufficiently small. We will register this fact in a brief remark.
Remark 3.2. If we look for solutions of type ![]() $X=Y \gt 0$, since
$X=Y \gt 0$, since ![]() $p,q\in (0,1)$,
$p,q\in (0,1)$, ![]() $\max\{\alpha,\beta\} \gt 1$, and
$\max\{\alpha,\beta\} \gt 1$, and ![]() $\max\{\theta,\gamma\} \gt 1$, it is easy to see that
$\max\{\theta,\gamma\} \gt 1$, it is easy to see that
 \begin{equation*}
X=Y=\max\{(2A\lambda)^{\frac{1}{1-q}},(2B\mu)^{\frac{1}{1-p}}\}
\end{equation*}
\begin{equation*}
X=Y=\max\{(2A\lambda)^{\frac{1}{1-q}},(2B\mu)^{\frac{1}{1-p}}\}
\end{equation*} with  $\max\{(2A\lambda)^{\frac{1}{1-q}},(2B\mu)^{\frac{1}{1-p}}\}\leq
\min\{(2C)^{\frac{-1}{\alpha+\beta-1}},(2D)^{\frac{-1}{\theta+\gamma-1}}\}$ satisfies Equation (3.1) and
$\max\{(2A\lambda)^{\frac{1}{1-q}},(2B\mu)^{\frac{1}{1-p}}\}\leq
\min\{(2C)^{\frac{-1}{\alpha+\beta-1}},(2D)^{\frac{-1}{\theta+\gamma-1}}\}$ satisfies Equation (3.1) and
 \begin{equation*}
X=Y=\min\{(2\lambda C)^{\frac{-1}{\alpha+\beta-1}},(2\mu D)^{\frac{-1}{\theta+\gamma-1}}\}
\end{equation*}
\begin{equation*}
X=Y=\min\{(2\lambda C)^{\frac{-1}{\alpha+\beta-1}},(2\mu D)^{\frac{-1}{\theta+\gamma-1}}\}
\end{equation*} with  $\max\{(2A)^{\frac{1}{1-q}},(2B)^{\frac{1}{1-p}}\}\leq
\min\{(2\lambda C)^{\frac{-1}{\alpha+\beta-1}},(2\mu D)^{\frac{-1}{\theta+\gamma-1}}\}$ satisfies Equation (3.2). Then, there is
$\max\{(2A)^{\frac{1}{1-q}},(2B)^{\frac{1}{1-p}}\}\leq
\min\{(2\lambda C)^{\frac{-1}{\alpha+\beta-1}},(2\mu D)^{\frac{-1}{\theta+\gamma-1}}\}$ satisfies Equation (3.2). Then, there is ![]() $\Lambda \gt 0$ such that Equations (3.1) and (3.2) always have solutions for all
$\Lambda \gt 0$ such that Equations (3.1) and (3.2) always have solutions for all ![]() $\lambda,\mu\in (0,\Lambda]$, so we are interested in analyzing cases where λ > 0 or µ > 0 can be arbitrarily large.
$\lambda,\mu\in (0,\Lambda]$, so we are interested in analyzing cases where λ > 0 or µ > 0 can be arbitrarily large.
Lemma 3.3. Suppose that ![]() $A,\,B,\,C,\,D \gt 0$, then there are
$A,\,B,\,C,\,D \gt 0$, then there are ![]() $\Lambda_{kij}=\Lambda_{kij}(A,B,C,D,$
$\Lambda_{kij}=\Lambda_{kij}(A,B,C,D,$ ![]() $\alpha,\beta,\gamma,\theta) \gt 0$ such that
$\alpha,\beta,\gamma,\theta) \gt 0$ such that
(i) If
 $(PW_1)$ holds, then the system (3.1) has a solution (X, Y) if
$(PW_1)$ holds, then the system (3.1) has a solution (X, Y) if
 \begin{equation*}
\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}}\leq\Lambda_{111}
\,\,\,\mbox{and}\,\,\,
\lambda^{\frac{\theta}{1-q}}\mu^{\frac{\gamma-1}{1-p}}\leq\Lambda_{211};
\end{equation*}
\begin{equation*}
\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}}\leq\Lambda_{111}
\,\,\,\mbox{and}\,\,\,
\lambda^{\frac{\theta}{1-q}}\mu^{\frac{\gamma-1}{1-p}}\leq\Lambda_{211};
\end{equation*}(ii) If
 $(PW_1)$ holds, then the system (3.2) has a solution if
$(PW_1)$ holds, then the system (3.2) has a solution if  $\lambda\leq\Lambda_{121}$ and
$\lambda\leq\Lambda_{121}$ and  $\mu\leq\Lambda_{221}$;
$\mu\leq\Lambda_{221}$;(iii) If
 $(PW_2)$ holds, then the system (3.1) has a solution if
$(PW_2)$ holds, then the system (3.1) has a solution if  $\lambda\leq\Lambda_{112}$ and
$\lambda\leq\Lambda_{112}$ and  $\mu\leq\Lambda_{212}$;
$\mu\leq\Lambda_{212}$;(iv) If
 $(PW_2)$ holds, then the system (3.2) has a solution if
$(PW_2)$ holds, then the system (3.2) has a solution if  $\lambda^{1-\gamma}
\mu^{\beta}\leq\Lambda_{122}$ and
$\lambda^{1-\gamma}
\mu^{\beta}\leq\Lambda_{122}$ and  $\lambda^\theta
\mu^{1-\alpha}\leq\Lambda_{222}$;
$\lambda^\theta
\mu^{1-\alpha}\leq\Lambda_{222}$;(v) If
 $(PW_3)$ holds, then the system (3.1) has a solution if
$(PW_3)$ holds, then the system (3.1) has a solution if  $\lambda\leq\Lambda_{113}$ and
$\lambda\leq\Lambda_{113}$ and  $\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}}\leq\Lambda_{213}$;
$\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}}\leq\Lambda_{213}$;(vi) If
 $(PW_3)$ holds, then the system (3.2) has a solution if
$(PW_3)$ holds, then the system (3.2) has a solution if  $\lambda\leq\Lambda_{123}$ and
$\lambda\leq\Lambda_{123}$ and  $\lambda^{1-\gamma}\mu^\beta\leq\Lambda_{223}. $
$\lambda^{1-\gamma}\mu^\beta\leq\Lambda_{223}. $
Proof. The Case (ii) and Case (iii) follow from Remark 3.2.
Case (i): It is enough to take  $X=(2A\lambda)^{\frac{1}{1-q}}$ and
$X=(2A\lambda)^{\frac{1}{1-q}}$ and  $Y=(2B\mu)^{\frac{1}{1-p}}$. Thus, we have
$Y=(2B\mu)^{\frac{1}{1-p}}$. Thus, we have ![]() $(X/2)=\lambda AX^q$ and
$(X/2)=\lambda AX^q$ and ![]() $(Y/2)= \mu BY^p$. On the other hand, if
$(Y/2)= \mu BY^p$. On the other hand, if  $\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}}\leq\Lambda_{111}:=(2A)^{\frac{-(\alpha-1)}{1-q}}(2B)^{\frac{-\beta}{1-p}}(2C)^{-1}$ and
$\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}}\leq\Lambda_{111}:=(2A)^{\frac{-(\alpha-1)}{1-q}}(2B)^{\frac{-\beta}{1-p}}(2C)^{-1}$ and
 \begin{equation*}
\lambda^{\frac{\theta}{1-q}}\mu^{\frac{\gamma-1}{1-p}}\leq\Lambda_{211}:=(2A)^{\frac{-\theta}{1-q}}(2B)^{\frac{-(\gamma-1)}{1-p}}(2D)^{-1},
\end{equation*}
\begin{equation*}
\lambda^{\frac{\theta}{1-q}}\mu^{\frac{\gamma-1}{1-p}}\leq\Lambda_{211}:=(2A)^{\frac{-\theta}{1-q}}(2B)^{\frac{-(\gamma-1)}{1-p}}(2D)^{-1},
\end{equation*} then ![]() $(X/2)\geq CX^\alpha Y^\beta$ and
$(X/2)\geq CX^\alpha Y^\beta$ and ![]() $(Y/2)\geq DX^\theta Y^\gamma$, and therefore X and Y satisfy Equation (3.1).
$(Y/2)\geq DX^\theta Y^\gamma$, and therefore X and Y satisfy Equation (3.1).
Case (iv): If
 \begin{equation*}
X:=((2D)^\beta(2C)^{1-\gamma}\lambda^{1-\gamma}\mu^\beta)^{\frac{-1}{\beta\theta-(1-\alpha)(1-\gamma)}}
\end{equation*}
\begin{equation*}
X:=((2D)^\beta(2C)^{1-\gamma}\lambda^{1-\gamma}\mu^\beta)^{\frac{-1}{\beta\theta-(1-\alpha)(1-\gamma)}}
\end{equation*}and
 \begin{equation*}
Y:=((2D)^{1-\alpha}(2C)^\theta\lambda^\theta\mu^{1-\alpha})^{\frac{-1}{\beta\theta-(1-\alpha)(1-\gamma)}},
\end{equation*}
\begin{equation*}
Y:=((2D)^{1-\alpha}(2C)^\theta\lambda^\theta\mu^{1-\alpha})^{\frac{-1}{\beta\theta-(1-\alpha)(1-\gamma)}},
\end{equation*} then we see that ![]() $X/2=\lambda C X^\alpha Y^\beta$ and
$X/2=\lambda C X^\alpha Y^\beta$ and ![]() $Y/2=\mu D X^\theta Y^\gamma$. Since
$Y/2=\mu D X^\theta Y^\gamma$. Since ![]() $\beta\theta-(1-\alpha)(1-\gamma) \gt 0$, we can choose
$\beta\theta-(1-\alpha)(1-\gamma) \gt 0$, we can choose ![]() $\Lambda_{122} \gt 0$ and
$\Lambda_{122} \gt 0$ and ![]() $\Lambda_{222} \gt 0$ such that
$\Lambda_{222} \gt 0$ such that ![]() $\lambda^{1-\gamma}\mu^\beta\leq\Lambda_{122}$ and
$\lambda^{1-\gamma}\mu^\beta\leq\Lambda_{122}$ and ![]() $\lambda^\theta\mu^{1-\alpha}\leq\Lambda_{222}$ imply
$\lambda^\theta\mu^{1-\alpha}\leq\Lambda_{222}$ imply ![]() $X/2\geq AX^q$ and
$X/2\geq AX^q$ and ![]() $Y/2\geq BY^p$. Therefore, X and Y satisfy Equation (3.2). Case (v): If we take
$Y/2\geq BY^p$. Therefore, X and Y satisfy Equation (3.2). Case (v): If we take  $X=(2A\lambda)^{\frac{1}{1-q}}$ and
$X=(2A\lambda)^{\frac{1}{1-q}}$ and  $Y=\max\{(2B\mu)^{\frac{1}{1-p}},\,(2D(2A\lambda)^{\frac{\theta}{1-q}})^{\frac{1}{1-\gamma}}\}$, then we have
$Y=\max\{(2B\mu)^{\frac{1}{1-p}},\,(2D(2A\lambda)^{\frac{\theta}{1-q}})^{\frac{1}{1-\gamma}}\}$, then we have ![]() $X/2=\lambda AX^q$ and
$X/2=\lambda AX^q$ and ![]() $Y\geq\mu BY^p +DX^\theta Y^\gamma$. Now we choose
$Y\geq\mu BY^p +DX^\theta Y^\gamma$. Now we choose ![]() $\Lambda_{113} \gt 0$ and
$\Lambda_{113} \gt 0$ and ![]() $\Lambda_{213} \gt 0$, in such a way that for
$\Lambda_{213} \gt 0$, in such a way that for ![]() $\lambda\leq\Lambda_{15}$ and
$\lambda\leq\Lambda_{15}$ and  $\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}}\leq\Lambda_{25}$ we have
$\lambda^{\frac{\alpha-1}{1-q}}\mu^{\frac{\beta}{1-p}}\leq\Lambda_{25}$ we have ![]() $X/2\geq CX^\alpha Y^\beta$, and therefore X and Y satisfy Equation (3.1).
$X/2\geq CX^\alpha Y^\beta$, and therefore X and Y satisfy Equation (3.1).
Case (vi): First of all, take ![]() $\overline{B}=\overline{B}(B,\gamma,p)$ such that
$\overline{B}=\overline{B}(B,\gamma,p)$ such that ![]() $Y\geq \overline{B} Y^\gamma \Rightarrow Y\geq 2BY^p$. Then, the solutions of the system
$Y\geq \overline{B} Y^\gamma \Rightarrow Y\geq 2BY^p$. Then, the solutions of the system
 \begin{equation}
\left\{
\begin{array}{lcl}
X &\geq& AX^q + \lambda CX^\alpha Y^\beta
\\
Y &\geq& \overline{B}Y^\gamma + 2\mu DX^\theta Y^\gamma
\\
&& X \gt 0, \,\, Y \gt 0,
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{lcl}
X &\geq& AX^q + \lambda CX^\alpha Y^\beta
\\
Y &\geq& \overline{B}Y^\gamma + 2\mu DX^\theta Y^\gamma
\\
&& X \gt 0, \,\, Y \gt 0,
\end{array}
\right.
\end{equation} are solutions of Equation (3.2). Since ![]() $\alpha\geq 1$, there are
$\alpha\geq 1$, there are ![]() $\Lambda_{123} \gt 0$ and
$\Lambda_{123} \gt 0$ and ![]() $\Lambda_{223} \gt 0$ such that, for all
$\Lambda_{223} \gt 0$ such that, for all ![]() $\lambda\leq\Lambda_{123}$ and
$\lambda\leq\Lambda_{123}$ and  $\lambda\mu^{\frac{\beta}{1-\gamma}}\leq\Lambda_{223}^{\frac{1}{1-\gamma}}$ (
$\lambda\mu^{\frac{\beta}{1-\gamma}}\leq\Lambda_{223}^{\frac{1}{1-\gamma}}$ (![]() $\lambda^{1-\gamma}\mu^\beta\leq\Lambda_{223}$), there is X > 0 satisfying
$\lambda^{1-\gamma}\mu^\beta\leq\Lambda_{223}$), there is X > 0 satisfying
 \begin{equation*}
X \geq AX^q + \lambda 2^{\frac{\beta}{1-\gamma}}\overline{B}^{\frac{\beta}{1-\gamma}}CX^\alpha +
\lambda\mu^{\frac{\beta}{1-\gamma}}2^{\frac{\beta}{1-\gamma}}(2D)^{\frac{\beta}{1-\gamma}}C
X^{\alpha+\frac{\beta\theta}{1-\gamma}}.
\end{equation*}
\begin{equation*}
X \geq AX^q + \lambda 2^{\frac{\beta}{1-\gamma}}\overline{B}^{\frac{\beta}{1-\gamma}}CX^\alpha +
\lambda\mu^{\frac{\beta}{1-\gamma}}2^{\frac{\beta}{1-\gamma}}(2D)^{\frac{\beta}{1-\gamma}}C
X^{\alpha+\frac{\beta\theta}{1-\gamma}}.
\end{equation*}So
 \begin{equation*}
\dfrac{X-AX^q}{\lambda CX^\alpha} \geq
2^{\frac{\beta}{1-\gamma}}\left(\overline{B}^{\frac{\beta}{1-\gamma}}+(2D\mu)^{\frac{\beta}{1-\gamma}}
X^{\frac{\beta\theta}{1-\gamma}}\right)\geq
\left(\overline{B}+2\mu D X^\theta\right)^{\frac{\beta}{1-\gamma}}.
\end{equation*}
\begin{equation*}
\dfrac{X-AX^q}{\lambda CX^\alpha} \geq
2^{\frac{\beta}{1-\gamma}}\left(\overline{B}^{\frac{\beta}{1-\gamma}}+(2D\mu)^{\frac{\beta}{1-\gamma}}
X^{\frac{\beta\theta}{1-\gamma}}\right)\geq
\left(\overline{B}+2\mu D X^\theta\right)^{\frac{\beta}{1-\gamma}}.
\end{equation*}Hence, if we take Y > 0 in such a way
 \begin{equation*}
\dfrac{X-AX^q}{\lambda CX^\alpha} \geq Y^\beta \geq
\left(\overline{B}+2\mu D X^\theta\right)^{\frac{\beta}{1-\gamma}},
\end{equation*}
\begin{equation*}
\dfrac{X-AX^q}{\lambda CX^\alpha} \geq Y^\beta \geq
\left(\overline{B}+2\mu D X^\theta\right)^{\frac{\beta}{1-\gamma}},
\end{equation*}then X > 0 and Y > 0 satisfy Equation (3.3).
Corollary 3.4. (Existence of super-solution)
Let  ${{e\in W^{2,s}(\overline{\Omega})\cap W_0^{1,s}(\Omega)\cap C^1(\overline{\Omega})}}$ be the unique positive solution of the problem
${{e\in W^{2,s}(\overline{\Omega})\cap W_0^{1,s}(\Omega)\cap C^1(\overline{\Omega})}}$ be the unique positive solution of the problem ![]() $-\Delta e=1$ in Ω, where e = 0 on
$-\Delta e=1$ in Ω, where e = 0 on ![]() $\partial\Omega$ (see [Reference Gilbarg and Trudinger31, Theorems 7.26 and 9.15]). Define
$\partial\Omega$ (see [Reference Gilbarg and Trudinger31, Theorems 7.26 and 9.15]). Define ![]() $A:=\|a\|_\infty \|e\|_\infty^q$,
$A:=\|a\|_\infty \|e\|_\infty^q$, ![]() $B:=\|b\|_\infty \|e\|_\infty^p$,
$B:=\|b\|_\infty \|e\|_\infty^p$, ![]() $C=\|c\|_\infty \|e\|_\infty^{\alpha+\beta}$ and
$C=\|c\|_\infty \|e\|_\infty^{\alpha+\beta}$ and ![]() $D:=\|d\|_\infty \|e\|_\infty^{\theta+\gamma}$. For
$D:=\|d\|_\infty \|e\|_\infty^{\theta+\gamma}$. For ![]() $\Lambda_{kij}$ found in Lemma 3.3, in each of the cases
$\Lambda_{kij}$ found in Lemma 3.3, in each of the cases ![]() $(i)-(vi)$, where
$(i)-(vi)$, where ![]() $\lambda,\,\mu\, \gt 0$ satisfy these conditions, there are
$\lambda,\,\mu\, \gt 0$ satisfy these conditions, there are  $\overline{u},\,\overline{v}\in W^{2,s}(\overline{\Omega})\cap W_0^{1,s}(\Omega)\cap C^1(\overline{\Omega})$ satisfying
$\overline{u},\,\overline{v}\in W^{2,s}(\overline{\Omega})\cap W_0^{1,s}(\Omega)\cap C^1(\overline{\Omega})$ satisfying ![]() $(\overline{\mathcal{S}}_{\lambda\mu})$.
$(\overline{\mathcal{S}}_{\lambda\mu})$.
Proof. If X > 0 and Y > 0 are solutions for Equation (3.1) or (3.2), then we see that ![]() $\overline{u}=Xe$ and
$\overline{u}=Xe$ and ![]() $\overline{v}=Ye$ satisfy
$\overline{v}=Ye$ satisfy ![]() $(\overline{\mathcal{S}}_{\lambda\mu})$.
$(\overline{\mathcal{S}}_{\lambda\mu})$.
In a manner akin to the definition of a super-solution, we define ![]() ${(\underline{u}, \underline{v})}$ as a sub-solution for
${(\underline{u}, \underline{v})}$ as a sub-solution for ![]() ${(\mathcal{P}_i)}$ subordinate to
${(\mathcal{P}_i)}$ subordinate to ![]() ${\overline{u}, \overline{v} \in L^\infty(\Omega) \setminus \{0\}}$ when
${\overline{u}, \overline{v} \in L^\infty(\Omega) \setminus \{0\}}$ when  $
{\underline{u}, \underline{v} \in W^{2,s}(\Omega) \cap W_0^{1,s}(\Omega) \cap C^1(\overline{\Omega})}
$ for all s > 1 and
$
{\underline{u}, \underline{v} \in W^{2,s}(\Omega) \cap W_0^{1,s}(\Omega) \cap C^1(\overline{\Omega})}
$ for all s > 1 and ![]() ${\underline{u}, \underline{v}}$ satisfy:
${\underline{u}, \underline{v}}$ satisfy:
 \begin{align}
\left\{
\begin{array}{ll}
-\Delta \underline{u}\leq f_\lambda(x,\underline{u},w)& \mbox{in}~~\Omega,\,\,\forall w\in[0,\overline{v}]
\\
-\Delta \underline{v}\leq g_\mu(x,z,\underline{v}) & \mbox{in}~~\Omega,\,\,\forall z\in[0,\overline{u}]
\\
\underline{v},\,\,\underline{v}\geq0& \mbox{in}~~\Omega
\\
\underline{u}=\underline{v}=0&\mbox{on}~~\partial\Omega
\\
\underline{u}\not\equiv 0,\,\underline{v}\not\equiv 0&\mbox{in}~~\Omega.
\end{array}
\right.
\end{align}
\begin{align}
\left\{
\begin{array}{ll}
-\Delta \underline{u}\leq f_\lambda(x,\underline{u},w)& \mbox{in}~~\Omega,\,\,\forall w\in[0,\overline{v}]
\\
-\Delta \underline{v}\leq g_\mu(x,z,\underline{v}) & \mbox{in}~~\Omega,\,\,\forall z\in[0,\overline{u}]
\\
\underline{v},\,\,\underline{v}\geq0& \mbox{in}~~\Omega
\\
\underline{u}=\underline{v}=0&\mbox{on}~~\partial\Omega
\\
\underline{u}\not\equiv 0,\,\underline{v}\not\equiv 0&\mbox{in}~~\Omega.
\end{array}
\right.
\end{align}Remark 3.5. A similar observation to that in Remark 3.1 holds for sub-solutions.
The sets ![]() $\mathcal{A}:=\{x\in\Omega\,\,|\,\,a(x) \gt a_1:=\|a\|_\infty/2\}$ and
$\mathcal{A}:=\{x\in\Omega\,\,|\,\,a(x) \gt a_1:=\|a\|_\infty/2\}$ and ![]() $\mathcal{B}:=\{x\in\Omega\,\,|\,\,b(x) \gt b_1:=\|b\|_\infty/2\}$ have positive Lebesgue measure. Furthermore,
$\mathcal{B}:=\{x\in\Omega\,\,|\,\,b(x) \gt b_1:=\|b\|_\infty/2\}$ have positive Lebesgue measure. Furthermore, ![]() $\Omega\setminus\mathcal{A}$ and
$\Omega\setminus\mathcal{A}$ and ![]() $\Omega\setminus\mathcal{B}$ can have zero Lebesgue measure, despite that we can set
$\Omega\setminus\mathcal{B}$ can have zero Lebesgue measure, despite that we can set ![]() $h,\,r\in L^\infty(\Omega)$ by
$h,\,r\in L^\infty(\Omega)$ by
 \begin{equation}
h(x)=
\left\{
\begin{array}{lll}
a_1&,&x\in \mathcal{A}
\\
-1&,&x\in\Omega\setminus\mathcal{A}
\end{array}
\right.
\,\,\,\,\,\,\,\,\,
r(x)=
\left\{
\begin{array}{lll}
b_1&,&x\in \mathcal{B}
\\
-1&,&x\in\Omega\setminus\mathcal{B}.
\end{array}
\right.
\end{equation}
\begin{equation}
h(x)=
\left\{
\begin{array}{lll}
a_1&,&x\in \mathcal{A}
\\
-1&,&x\in\Omega\setminus\mathcal{A}
\end{array}
\right.
\,\,\,\,\,\,\,\,\,
r(x)=
\left\{
\begin{array}{lll}
b_1&,&x\in \mathcal{B}
\\
-1&,&x\in\Omega\setminus\mathcal{B}.
\end{array}
\right.
\end{equation} We will see that in some cases, for a small ɛ > 0, we have sub-solutions of the type ![]() $\underline{u}=\varepsilon\varphi_{1h\Omega}$ and
$\underline{u}=\varepsilon\varphi_{1h\Omega}$ and ![]() $\underline{v}=\varepsilon\varphi_{1r\Omega}$. However, this approach does not work when
$\underline{v}=\varepsilon\varphi_{1r\Omega}$. However, this approach does not work when ![]() $c^-(x) \not\equiv 0$,
$c^-(x) \not\equiv 0$, ![]() $d^-(x) \not\equiv 0$,
$d^-(x) \not\equiv 0$, ![]() $q \lt \alpha \lt 1$, or
$q \lt \alpha \lt 1$, or ![]() $p \lt \gamma \lt 1$. In order to overcome this obstacle, we will obtain another type of sub-solution. For that, we will use the variational method.
$p \lt \gamma \lt 1$. In order to overcome this obstacle, we will obtain another type of sub-solution. For that, we will use the variational method.
Proposition 3.6. Let ![]() $m\in L^\infty(\Omega)\setminus\{0\}$ with
$m\in L^\infty(\Omega)\setminus\{0\}$ with ![]() $m(x)\geq 0$ in Ω. For all
$m(x)\geq 0$ in Ω. For all ![]() $0 \lt r_1 \lt r_2\leq 1$,
$0 \lt r_1 \lt r_2\leq 1$, ![]() $K\geq 0$, and ɛ > 0, the auxiliary problem
$K\geq 0$, and ɛ > 0, the auxiliary problem ![]() $(\mathcal{P}_\varepsilon)$:
$(\mathcal{P}_\varepsilon)$:
 \begin{align}
\left\{
\begin{array}{ll}
-\Delta u=\varepsilon m(x)u^{r_1}-Ku^{r_2}& \text{in}~~\Omega
\\
0\not\equiv u\geq 0& \text{in}~~\Omega
\\
u=0&\text{on}~~\partial\Omega,
\end{array}
\right.
\end{align}
\begin{align}
\left\{
\begin{array}{ll}
-\Delta u=\varepsilon m(x)u^{r_1}-Ku^{r_2}& \text{in}~~\Omega
\\
0\not\equiv u\geq 0& \text{in}~~\Omega
\\
u=0&\text{on}~~\partial\Omega,
\end{array}
\right.
\end{align} has a solution  $u\in W^{2,s}(\Omega)\cap W_0^{1,s}(\Omega)\cap C^1(\overline{\Omega})$, for all s > 1. Moreover, we have
$u\in W^{2,s}(\Omega)\cap W_0^{1,s}(\Omega)\cap C^1(\overline{\Omega})$, for all s > 1. Moreover, we have  $u\leq \varepsilon^{\frac{1}{1-r_1}}Me$ in Ω, where
$u\leq \varepsilon^{\frac{1}{1-r_1}}Me$ in Ω, where  ${{e\in W^{2,s}(\Omega)\cap W_0^{1,s}(\Omega)\cap C^1(\overline{\Omega})}}$ is the unique solution of
${{e\in W^{2,s}(\Omega)\cap W_0^{1,s}(\Omega)\cap C^1(\overline{\Omega})}}$ is the unique solution of ![]() $-\Delta e=1$ in Ω, and
$-\Delta e=1$ in Ω, and ![]() $M=M(r_1,\|m\|_\infty,\|e\|_\infty)$.
$M=M(r_1,\|m\|_\infty,\|e\|_\infty)$.
Proof. Let ![]() $I_\varepsilon:H_0^1(\Omega)\rightarrow\mathbb{R}$,
$I_\varepsilon:H_0^1(\Omega)\rightarrow\mathbb{R}$, ![]() $I_\varepsilon\in C^1$ given by
$I_\varepsilon\in C^1$ given by
 \begin{equation*}
I_\varepsilon(u):=\dfrac{1}{2}\int_\Omega\left(|\nabla u|^2+\dfrac{2K}{r_2+1}|u|^{r_2+1}\right)\,\mathrm{d}x
-\dfrac{\lambda}{r_1+1}\int_\Omega m(x)|u|^{r_1+1}\,\mathrm{d}x.
\end{equation*}
\begin{equation*}
I_\varepsilon(u):=\dfrac{1}{2}\int_\Omega\left(|\nabla u|^2+\dfrac{2K}{r_2+1}|u|^{r_2+1}\right)\,\mathrm{d}x
-\dfrac{\lambda}{r_1+1}\int_\Omega m(x)|u|^{r_1+1}\,\mathrm{d}x.
\end{equation*} Since ![]() $H_0^1(\Omega)\hookrightarrow L^{r_1+1}(\Omega)$, then for some R > 0, we have
$H_0^1(\Omega)\hookrightarrow L^{r_1+1}(\Omega)$, then for some R > 0, we have
 \begin{equation}
I_\varepsilon(u)\geq 0,\,\,\,\,\text{for all}\,\,\,\,\|u\|:=\|u\|_{H_0^1(\Omega)}=\left(\int_\Omega|\nabla u|^2dx\right)^{\frac{1}{2}}=R.
\end{equation}
\begin{equation}
I_\varepsilon(u)\geq 0,\,\,\,\,\text{for all}\,\,\,\,\|u\|:=\|u\|_{H_0^1(\Omega)}=\left(\int_\Omega|\nabla u|^2dx\right)^{\frac{1}{2}}=R.
\end{equation} Choosing ![]() $\varphi\in H_0^1(\Omega)$ with
$\varphi\in H_0^1(\Omega)$ with  $\int_\Omega m(x)\varphi\,\mathrm{d}x \gt 0$, we see that
$\int_\Omega m(x)\varphi\,\mathrm{d}x \gt 0$, we see that  $\lim_{t\rightarrow 0^+}t^{-(r_1+1)}I_\varepsilon(t\varphi) \lt 0$, then we get
$\lim_{t\rightarrow 0^+}t^{-(r_1+1)}I_\varepsilon(t\varphi) \lt 0$, then we get
 \begin{equation*}
c_0:=\inf \left\{I_\varepsilon(u)\,|\, u\in H_0^1(\Omega)\,\text{and}\, \|u\|\leq R\right\} \lt 0.
\end{equation*}
\begin{equation*}
c_0:=\inf \left\{I_\varepsilon(u)\,|\, u\in H_0^1(\Omega)\,\text{and}\, \|u\|\leq R\right\} \lt 0.
\end{equation*} A standard compactness argument provides ![]() $u_0\in H_0^1(\Omega)$ with
$u_0\in H_0^1(\Omega)$ with ![]() $\|u_0\|\leq R$ such that
$\|u_0\|\leq R$ such that ![]() $I_\varepsilon(u_0)=c_0 \lt 0$, so
$I_\varepsilon(u_0)=c_0 \lt 0$, so ![]() $u_0\not\equiv 0$. Since
$u_0\not\equiv 0$. Since ![]() $I_\varepsilon(u_0)=I_\varepsilon(|u_0|)$, we will suppose
$I_\varepsilon(u_0)=I_\varepsilon(|u_0|)$, we will suppose ![]() $u_0\geq 0$. From Equation (3.5), we get
$u_0\geq 0$. From Equation (3.5), we get ![]() $\|u_0\| \lt R$. Then
$\|u_0\| \lt R$. Then ![]() $I'_\varepsilon(u_0)=0$, hence u 0 is a weak solution for
$I'_\varepsilon(u_0)=0$, hence u 0 is a weak solution for ![]() $(\mathcal{P}_\varepsilon)$. From [Reference Struwe43, Lemma B3, p. 270], we obtain
$(\mathcal{P}_\varepsilon)$. From [Reference Struwe43, Lemma B3, p. 270], we obtain ![]() ${u_0 \in L^s(\Omega)}$ for all s > 1 (since
${u_0 \in L^s(\Omega)}$ for all s > 1 (since ![]() ${r_2 \leq 1}$, this can also be derived using a bootstrap argument). By [Reference Gilbarg and Trudinger31, Theorems 7.26 and 9.15], it follows that
${r_2 \leq 1}$, this can also be derived using a bootstrap argument). By [Reference Gilbarg and Trudinger31, Theorems 7.26 and 9.15], it follows that  ${u_0 \in W^{2,s}(\Omega) \cap W_0^{1,s}(\Omega) \cap C^1(\overline{\Omega})}$ for all s > 1. Now observe that for
${u_0 \in W^{2,s}(\Omega) \cap W_0^{1,s}(\Omega) \cap C^1(\overline{\Omega})}$ for all s > 1. Now observe that for  $t=\varepsilon^{\frac{1}{1-r_1}}(\|m\|_\infty \|e\|_\infty^{r_1})^{\frac{1}{1-r_1}}$, we have
$t=\varepsilon^{\frac{1}{1-r_1}}(\|m\|_\infty \|e\|_\infty^{r_1})^{\frac{1}{1-r_1}}$, we have ![]() $-\Delta (te)\geq \varepsilon m(x)(t e)^{r_1}$ in Ω. Since
$-\Delta (te)\geq \varepsilon m(x)(t e)^{r_1}$ in Ω. Since ![]() $-\Delta u_0\leq \varepsilon m(x) u_0^{r_1}$ in Ω, we can invoke Lemma 2.1 to obtain
$-\Delta u_0\leq \varepsilon m(x) u_0^{r_1}$ in Ω, we can invoke Lemma 2.1 to obtain ![]() $u_0\leq t e$.
$u_0\leq t e$.
Remark 3.7. Although we do not know if the solution u 0 is positive, observe that the set ![]() $\Omega_0:=\left\{x\in\overline{\Omega}\,|\,u_0(x)=0\right\}$ has empty interior. Otherwise, if there is
$\Omega_0:=\left\{x\in\overline{\Omega}\,|\,u_0(x)=0\right\}$ has empty interior. Otherwise, if there is ![]() $B_r\subset\overline{\Omega}_0$, then we can take
$B_r\subset\overline{\Omega}_0$, then we can take ![]() $\varphi\in C_c^\infty(\Omega)$ with
$\varphi\in C_c^\infty(\Omega)$ with ![]() $\text{supp}\,\varphi\subset B_r$. Therefore, for a small t > 0, we obtain
$\text{supp}\,\varphi\subset B_r$. Therefore, for a small t > 0, we obtain ![]() $I_\varepsilon(u_0+t\varphi)=I_\varepsilon(u_0)+I_\varepsilon(t\varphi) \lt I_\varepsilon(u_0)$, which is a contradiction.
$I_\varepsilon(u_0+t\varphi)=I_\varepsilon(u_0)+I_\varepsilon(t\varphi) \lt I_\varepsilon(u_0)$, which is a contradiction.
Remark 3.8. If ![]() $m_0:=\inf_\Omega m(x) \gt 0$, since
$m_0:=\inf_\Omega m(x) \gt 0$, since ![]() $r_2 \gt r_1$, then we get for M > 0 large
$r_2 \gt r_1$, then we get for M > 0 large ![]() $-\Delta u=\varepsilon m(x)u^{r_1}-Ku^{r_2}\geq \varepsilon m_0 u^{r_1}-Ku^{r_2}\geq -Mu$ in Ω, so the strong maximum principle provides u > 0 in Ω (see [Reference Gilbarg and Trudinger31, Theorem 8.19]).
$-\Delta u=\varepsilon m(x)u^{r_1}-Ku^{r_2}\geq \varepsilon m_0 u^{r_1}-Ku^{r_2}\geq -Mu$ in Ω, so the strong maximum principle provides u > 0 in Ω (see [Reference Gilbarg and Trudinger31, Theorem 8.19]).
Lemma 3.9. (Existence of sub-solutions)
Let ![]() $(\overline{u},\overline{v})=(\overline{u}_{\lambda\mu},\overline{v}_{\lambda\mu})$ be the super-solution obtained in Corollary 3.4 under the conditions (i)–(vi) of Lemma 3.3. Suppose that
$(\overline{u},\overline{v})=(\overline{u}_{\lambda\mu},\overline{v}_{\lambda\mu})$ be the super-solution obtained in Corollary 3.4 under the conditions (i)–(vi) of Lemma 3.3. Suppose that ![]() $(P_1)$–
$(P_1)$–![]() $(P_2)$ hold. Consider the following hypotheses:
$(P_2)$ hold. Consider the following hypotheses:
 \begin{equation*}
\begin{array}{ll}
(\underline{H}_1) c(x)\geq 0 \mbox{ in } \Omega; & (\underline{H}_3) d(x)\geq 0 \mbox{ in } \Omega; \\
(\underline{H}_2) \alpha \gt q; & (\underline{H}_4) \gamma \gt p.\\
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ll}
(\underline{H}_1) c(x)\geq 0 \mbox{ in } \Omega; & (\underline{H}_3) d(x)\geq 0 \mbox{ in } \Omega; \\
(\underline{H}_2) \alpha \gt q; & (\underline{H}_4) \gamma \gt p.\\
\end{array}
\end{equation*} If ![]() $(\underline{H}_1)$ or
$(\underline{H}_1)$ or ![]() $(\underline{H}_2)$ holds and if
$(\underline{H}_2)$ holds and if ![]() $(\underline{H}_3)$ or
$(\underline{H}_3)$ or ![]() $(\underline{H}_4)$ holds, then there are
$(\underline{H}_4)$ holds, then there are ![]() $\underline{u}$ and
$\underline{u}$ and ![]() $\underline{v}$ satisfying
$\underline{v}$ satisfying ![]() $(\underline{\mathcal{S}}_{\lambda\mu})$.
$(\underline{\mathcal{S}}_{\lambda\mu})$.
Proof. Without loss of generality, we will only obtain sub-solutions to ![]() $(\mathcal{P}_1)$. To illustrate the other cases, let us initially consider that α > 1 and γ > 1. Let h and r be defined in Equation (3.4). We set
$(\mathcal{P}_1)$. To illustrate the other cases, let us initially consider that α > 1 and γ > 1. Let h and r be defined in Equation (3.4). We set ![]() $\varphi_{1h}:=\varphi_{1h\Omega}$ and
$\varphi_{1h}:=\varphi_{1h\Omega}$ and ![]() $\varphi_{1r}:=\varphi_{1r\Omega}$. We can choose ɛ > 0 small in such a way:
$\varphi_{1r}:=\varphi_{1r\Omega}$. We can choose ɛ > 0 small in such a way:
 \begin{equation}
\left\{
\begin{array}{rll}
\varepsilon\lambda_{1h} \varphi_{1h}&\leq\lambda a_1(\varepsilon\varphi_{1h})^q-\|c\|_\infty (\varepsilon\varphi_{1h})^\alpha\|\overline{v}\|_\infty^\beta & x\in \mathcal{A}
\\
-\varepsilon\lambda_{1h} \varphi_{1h}&\leq-\|c\|_\infty (\varepsilon\varphi_{1h})^\alpha \|\overline{v}\|_\infty^\beta & x\in\Omega\setminus \mathcal{A}
\\
\varepsilon\lambda_{1r} \varphi_{1r}&\leq\mu b_1(\varepsilon\varphi_{1r})^p-\|d\|_\infty\|\overline{u}\|_\infty^\theta(\varepsilon\varphi_{1r})^\gamma & x\in \mathcal{B}
\\
-\varepsilon\lambda_{1r} \varphi_{1r}&\leq-\|d\|_\infty\|\overline{u}\|_\infty^\theta(\varepsilon\varphi_{1r})^\gamma & x\in\Omega\setminus \mathcal{B}.
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{rll}
\varepsilon\lambda_{1h} \varphi_{1h}&\leq\lambda a_1(\varepsilon\varphi_{1h})^q-\|c\|_\infty (\varepsilon\varphi_{1h})^\alpha\|\overline{v}\|_\infty^\beta & x\in \mathcal{A}
\\
-\varepsilon\lambda_{1h} \varphi_{1h}&\leq-\|c\|_\infty (\varepsilon\varphi_{1h})^\alpha \|\overline{v}\|_\infty^\beta & x\in\Omega\setminus \mathcal{A}
\\
\varepsilon\lambda_{1r} \varphi_{1r}&\leq\mu b_1(\varepsilon\varphi_{1r})^p-\|d\|_\infty\|\overline{u}\|_\infty^\theta(\varepsilon\varphi_{1r})^\gamma & x\in \mathcal{B}
\\
-\varepsilon\lambda_{1r} \varphi_{1r}&\leq-\|d\|_\infty\|\overline{u}\|_\infty^\theta(\varepsilon\varphi_{1r})^\gamma & x\in\Omega\setminus \mathcal{B}.
\end{array}
\right.
\end{equation} Taking ![]() $\underline{u}=\varepsilon\varphi_{1h}$ and
$\underline{u}=\varepsilon\varphi_{1h}$ and ![]() $\underline{v}=\varepsilon\varphi_{1r}$ in view of Equation (3.6), we have that
$\underline{v}=\varepsilon\varphi_{1r}$ in view of Equation (3.6), we have that ![]() $\underline{u}$ and
$\underline{u}$ and ![]() $\underline{v}$ satisfy
$\underline{v}$ satisfy ![]() $(\underline{\mathcal{S}}_{\lambda\mu})$.
$(\underline{\mathcal{S}}_{\lambda\mu})$.
If ![]() $q \lt \alpha\leq 1$ for ɛ > 0, we set uɛ as the solution of the problem
$q \lt \alpha\leq 1$ for ɛ > 0, we set uɛ as the solution of the problem ![]() $(\mathcal{P}_\varepsilon)$ with
$(\mathcal{P}_\varepsilon)$ with ![]() $K=\|c\|_\infty \|\overline{v}\|^\beta_\infty$ (see Proposition 3.6),
$K=\|c\|_\infty \|\overline{v}\|^\beta_\infty$ (see Proposition 3.6), ![]() $r_1=q$, and
$r_1=q$, and ![]() $r_2=\alpha$. Then for ɛ > 0 sufficiently small, we have
$r_2=\alpha$. Then for ɛ > 0 sufficiently small, we have
Since  $u_\varepsilon\leq \varepsilon^{\frac{1}{1-q}}Me$ in Ω, then for ɛ > 0 sufficiently small, we have
$u_\varepsilon\leq \varepsilon^{\frac{1}{1-q}}Me$ in Ω, then for ɛ > 0 sufficiently small, we have ![]() $u_\varepsilon\leq \overline{u}$, so we set
$u_\varepsilon\leq \overline{u}$, so we set ![]() $\underline{u}=u_\varepsilon$. If
$\underline{u}=u_\varepsilon$. If ![]() $p \lt \gamma\leq 1$, in the same way we set
$p \lt \gamma\leq 1$, in the same way we set  $0\leq v_\varepsilon \in W^{2,s}(\Omega)\cap W_0^{1,s}(\Omega)\cap C^1(\overline{\Omega})$ as the non-trivial solution of the problem
$0\leq v_\varepsilon \in W^{2,s}(\Omega)\cap W_0^{1,s}(\Omega)\cap C^1(\overline{\Omega})$ as the non-trivial solution of the problem  $-\Delta v_\varepsilon=\varepsilon b(x)v_\varepsilon^p-\widehat{K} v_\varepsilon^\gamma$ with
$-\Delta v_\varepsilon=\varepsilon b(x)v_\varepsilon^p-\widehat{K} v_\varepsilon^\gamma$ with  $\widehat{K}=\|d\|_\infty \|\overline{u}\|^\theta_\infty$. So, we set
$\widehat{K}=\|d\|_\infty \|\overline{u}\|^\theta_\infty$. So, we set ![]() $\underline{v}=v_\varepsilon$ for a sufficiently small ɛ > 0. If
$\underline{v}=v_\varepsilon$ for a sufficiently small ɛ > 0. If ![]() $c(x)\geq 0$ in Ω, then it is easy to check that
$c(x)\geq 0$ in Ω, then it is easy to check that ![]() $\varepsilon\varphi_{1a\Omega}$ satisfies the first inequality of
$\varepsilon\varphi_{1a\Omega}$ satisfies the first inequality of ![]() $(\underline{\mathcal{S}}_{\lambda\mu})$ for ɛ > 0 sufficiently small. If
$(\underline{\mathcal{S}}_{\lambda\mu})$ for ɛ > 0 sufficiently small. If ![]() $d(x)\geq 0$ in Ω, then
$d(x)\geq 0$ in Ω, then ![]() $\varepsilon\varphi_{1b\Omega}$ satisfies the second inequality of
$\varepsilon\varphi_{1b\Omega}$ satisfies the second inequality of ![]() $(\underline{\mathcal{S}}_{\lambda\mu})$. In short, we have that
$(\underline{\mathcal{S}}_{\lambda\mu})$. In short, we have that ![]() $\underline{u}$ assumes one of the following forms:
$\underline{u}$ assumes one of the following forms: ![]() $\varepsilon\varphi_{1a\Omega}$,
$\varepsilon\varphi_{1a\Omega}$, ![]() $\varepsilon\varphi_{1h}$, uɛ, and
$\varepsilon\varphi_{1h}$, uɛ, and ![]() $\underline{v}$ assumes one of the following forms:
$\underline{v}$ assumes one of the following forms: ![]() $\varepsilon\varphi_{1b\Omega}$,
$\varepsilon\varphi_{1b\Omega}$, ![]() $\varepsilon\varphi_{1r}$, vɛ.
$\varepsilon\varphi_{1r}$, vɛ.
4. Existence of positive solution: global and local results
This section is devoted to the proof of Theorem 1.4.
Proof of Theorem 1.4-(i)
Suppose that ![]() $(PW_j)$ holds and take
$(PW_j)$ holds and take ![]() $\Lambda_{1ij}, \,\Lambda_{2ij} \gt 0$ given by Lemma 3.3 with
$\Lambda_{1ij}, \,\Lambda_{2ij} \gt 0$ given by Lemma 3.3 with ![]() $A=\|a\|_\infty+1$,
$A=\|a\|_\infty+1$, ![]() $B=\|b\|_\infty+1$,
$B=\|b\|_\infty+1$, ![]() $C=\|c\|_\infty$ and
$C=\|c\|_\infty$ and ![]() $D=\|d\|_\infty$. Under conditions
$D=\|d\|_\infty$. Under conditions ![]() $(H_l)$ and
$(H_l)$ and ![]() $(H_s)$, we will get positive solutions for the problem
$(H_s)$, we will get positive solutions for the problem ![]() $(\mathcal{P}_i)$ when
$(\mathcal{P}_i)$ when ![]() $\lambda^{\tau_{1j}}\mu^{\sigma_{1j}}\leq \Lambda_{1ij}$ and
$\lambda^{\tau_{1j}}\mu^{\sigma_{1j}}\leq \Lambda_{1ij}$ and  $\lambda^{\overline{\tau}_{2j}}\mu^{\overline{\sigma}_{2j}}\leq \Lambda_{2ij}$. We will obtain the solutions by an iteration argument. In order to do this, for Q > 0 we define
$\lambda^{\overline{\tau}_{2j}}\mu^{\overline{\sigma}_{2j}}\leq \Lambda_{2ij}$. We will obtain the solutions by an iteration argument. In order to do this, for Q > 0 we define
 \begin{equation*}
\begin{array}{lcl}
\mathcal{F}_\lambda(x,u,v)&:=&Qu+f_\lambda(x,u,v)
\\
\mathcal{G}_\mu(x,u,v)&:=&Qv+g_\mu(x,u,v),
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lcl}
\mathcal{F}_\lambda(x,u,v)&:=&Qu+f_\lambda(x,u,v)
\\
\mathcal{G}_\mu(x,u,v)&:=&Qv+g_\mu(x,u,v),
\end{array}
\end{equation*} where fλ and gµ were defined in § 3. The main difficulty here is that if ![]() $x\in\Omega$ satisfies
$x\in\Omega$ satisfies ![]() $a(x)=0$,
$a(x)=0$, ![]() $q \lt \alpha \lt 1$,
$q \lt \alpha \lt 1$, ![]() $c(x) \lt 0$ and
$c(x) \lt 0$ and ![]() $v(x) \gt 0$, then for all Q > 0 the function
$v(x) \gt 0$, then for all Q > 0 the function ![]() $t\mapsto \mathcal{F}_\lambda(x,t,v(x))$ is strictly decreasing for t > 0 close to zero, while if
$t\mapsto \mathcal{F}_\lambda(x,t,v(x))$ is strictly decreasing for t > 0 close to zero, while if ![]() $a(x) \gt 0$ and
$a(x) \gt 0$ and ![]() $v(x) \gt 0$, for all
$v(x) \gt 0$, for all ![]() $t_0 \gt 0$ there is Q > 0 large such that the function
$t_0 \gt 0$ there is Q > 0 large such that the function ![]() $t\mapsto \mathcal{F}_\lambda(x,t,v(x))$ is non-decreasing for t > 0 in
$t\mapsto \mathcal{F}_\lambda(x,t,v(x))$ is non-decreasing for t > 0 in ![]() $[0,t_0]$. The same phenomenon occurs with the function
$[0,t_0]$. The same phenomenon occurs with the function ![]() $t\mapsto\mathcal{G}_\mu(x,u(x),t)$. In this situation, we cannot guarantee that the functions are non-decreasing uniformly in
$t\mapsto\mathcal{G}_\mu(x,u(x),t)$. In this situation, we cannot guarantee that the functions are non-decreasing uniformly in ![]() $x\in\Omega$. Therefore, the iteration argument does not work. In order to get around this problem, we defined
$x\in\Omega$. Therefore, the iteration argument does not work. In order to get around this problem, we defined ![]() $a_k(x):=a(x)+1/k$ and
$a_k(x):=a(x)+1/k$ and ![]() $b_k(x):=b(x)+1/k$. The functions
$b_k(x):=b(x)+1/k$. The functions ![]() $f^k_\lambda(x,u,v)$ and
$f^k_\lambda(x,u,v)$ and  $g^k_\mu(x,u,v)$ are the functions
$g^k_\mu(x,u,v)$ are the functions ![]() $f_\lambda(x,u,v)$ and
$f_\lambda(x,u,v)$ and ![]() $g_\mu(x,u,v)$ with
$g_\mu(x,u,v)$ with ![]() $a_k(x)$ and
$a_k(x)$ and ![]() $b_k(x)$ instead of a(x) and b(x). In view of our choice of
$b_k(x)$ instead of a(x) and b(x). In view of our choice of ![]() $A,B,C,D$, Corollary 3.4 provides
$A,B,C,D$, Corollary 3.4 provides  $\overline{u},\overline{v}\in W^{2,s}(\Omega)\cap W_0^{1,s}(\Omega)\cap C^1(\overline{\Omega})$ for all s > 1, satisfying
$\overline{u},\overline{v}\in W^{2,s}(\Omega)\cap W_0^{1,s}(\Omega)\cap C^1(\overline{\Omega})$ for all s > 1, satisfying  $(\overline{\mathcal{S}}^k_{\lambda\mu})$ where
$(\overline{\mathcal{S}}^k_{\lambda\mu})$ where
 \begin{align}
\mbox{for all }\,\,k\in\mathbb{N}\,\,
\left\{
\begin{array}{ll}
-\Delta \overline{u}\geq f^k_\lambda(x,z,w)& \mbox{in}~~\Omega,\,\,\,\, \forall z\in[0,\overline{u}],\,\,w\in[0,\overline{v}]
\\
-\Delta \overline{v}\geq g^k_\mu(x,z,w) &\mbox{in}~~\Omega,\,\,\,\,\forall z\in[0,\overline{u}],\,\,w\in[0,\overline{v}]
\\
\overline{u},\,\,\overline{v} \gt 0& \mbox{in}~~\Omega
\\
\overline{u}=\overline{v}=0&\mbox{on}~~\partial\Omega.
\end{array}
\right.\\[-24pt] \nonumber
\end{align}
\begin{align}
\mbox{for all }\,\,k\in\mathbb{N}\,\,
\left\{
\begin{array}{ll}
-\Delta \overline{u}\geq f^k_\lambda(x,z,w)& \mbox{in}~~\Omega,\,\,\,\, \forall z\in[0,\overline{u}],\,\,w\in[0,\overline{v}]
\\
-\Delta \overline{v}\geq g^k_\mu(x,z,w) &\mbox{in}~~\Omega,\,\,\,\,\forall z\in[0,\overline{u}],\,\,w\in[0,\overline{v}]
\\
\overline{u},\,\,\overline{v} \gt 0& \mbox{in}~~\Omega
\\
\overline{u}=\overline{v}=0&\mbox{on}~~\partial\Omega.
\end{array}
\right.\\[-24pt] \nonumber
\end{align} Since ![]() $(H_l)$ and
$(H_l)$ and ![]() $(H_s)$ hold, then
$(H_s)$ hold, then  $(\underline{H}_{l_1})$ and
$(\underline{H}_{l_1})$ and  $(\underline{H}_{l_2})$ hold for some
$(\underline{H}_{l_2})$ hold for some ![]() $l_1\in\{1,2\}$ and
$l_1\in\{1,2\}$ and ![]() $l_2\in\{3,4\}$. Then we are under the hypotheses of Lemma 3.9. Therefore, there are
$l_2\in\{3,4\}$. Then we are under the hypotheses of Lemma 3.9. Therefore, there are ![]() $\underline{u}\leq\overline{u}$ and
$\underline{u}\leq\overline{u}$ and ![]() $\underline{v}\leq \overline{v}$ satisfying
$\underline{v}\leq \overline{v}$ satisfying ![]() $(\underline{\mathcal{S}}_{\lambda\mu})$ (now we are considering the problem with
$(\underline{\mathcal{S}}_{\lambda\mu})$ (now we are considering the problem with ![]() $f_\lambda(x,u,v)$ and
$f_\lambda(x,u,v)$ and ![]() $g_\mu(x,u,v)$). For all Q > 0, we define
$g_\mu(x,u,v)$). For all Q > 0, we define
 \begin{equation*}
\begin{array}{lcl}
\mathcal{F}^k_\lambda(x,u,v) &:=& Qu + f_\lambda^k (x,u,v) \\
\mathcal{G}^k_\mu(x,u,v) &:=& Qv + g_\mu^k(x,u,v).
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lcl}
\mathcal{F}^k_\lambda(x,u,v) &:=& Qu + f_\lambda^k (x,u,v) \\
\mathcal{G}^k_\mu(x,u,v) &:=& Qv + g_\mu^k(x,u,v).
\end{array}
\end{equation*} If ![]() $c(x)\geq 0$ (i.e.
$c(x)\geq 0$ (i.e. ![]() $(\underline{H}_1)$ holds), then
$(\underline{H}_1)$ holds), then ![]() $\partial_t\mathcal{F}^k_\lambda(x,t,s)\geq 0$ for all Q > 0. If
$\partial_t\mathcal{F}^k_\lambda(x,t,s)\geq 0$ for all Q > 0. If ![]() $(\underline{H}_2)$ holds, then
$(\underline{H}_2)$ holds, then ![]() $\alpha \gt q$. Therefore, for all
$\alpha \gt q$. Therefore, for all ![]() $t_0 \gt 0$ and
$t_0 \gt 0$ and ![]() $s_0 \gt 0$, for Q > 0 sufficiently large, we have
$s_0 \gt 0$, for Q > 0 sufficiently large, we have ![]() $\partial_t\mathcal{F}^k_\lambda(x,t,s)\geq 0$ for
$\partial_t\mathcal{F}^k_\lambda(x,t,s)\geq 0$ for ![]() $x\in\Omega$,
$x\in\Omega$, ![]() $t\in[0,t_0]$ and
$t\in[0,t_0]$ and ![]() $s\in[0,s_0]$. Analogously, we can suppose for the same Q > 0 that
$s\in[0,s_0]$. Analogously, we can suppose for the same Q > 0 that  $\partial_s\mathcal{G}_\mu^k(x,t,s) \gt 0$ for
$\partial_s\mathcal{G}_\mu^k(x,t,s) \gt 0$ for ![]() $x\in\Omega$,
$x\in\Omega$, ![]() $t\in[0,t_0]$ and
$t\in[0,t_0]$ and ![]() $s_0\in[0,s_0]$. The last two expressions give us for some Q > 0
$s_0\in[0,s_0]$. The last two expressions give us for some Q > 0
 \begin{equation}
\left\{
\begin{array}{lcl}
0\leq s_1\leq s_2\leq \|\overline{u}\|_\infty&
\\
0\leq t_1\leq t_2\leq \|\overline{v}\|_\infty&
\\
0\leq s\leq \|\overline{u}\|_\infty&
\\
0\leq t\leq \|\overline{v}\|_\infty&
\end{array}
\right.
\Longrightarrow\,\,\,
\left\{
\begin{array}{lcl}
0\leq \mathcal{F}_\lambda^k(x,s_1,t)&\leq& \mathcal{F}^k_\lambda(x,s_2,t)
\\
0\leq \mathcal{G}_\mu^k(x,s,t_1)&\leq& \mathcal{G}^k_\mu(x,s,t_2).
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{lcl}
0\leq s_1\leq s_2\leq \|\overline{u}\|_\infty&
\\
0\leq t_1\leq t_2\leq \|\overline{v}\|_\infty&
\\
0\leq s\leq \|\overline{u}\|_\infty&
\\
0\leq t\leq \|\overline{v}\|_\infty&
\end{array}
\right.
\Longrightarrow\,\,\,
\left\{
\begin{array}{lcl}
0\leq \mathcal{F}_\lambda^k(x,s_1,t)&\leq& \mathcal{F}^k_\lambda(x,s_2,t)
\\
0\leq \mathcal{G}_\mu^k(x,s,t_1)&\leq& \mathcal{G}^k_\mu(x,s,t_2).
\end{array}
\right.
\end{equation} We define the monotone iteration for ![]() $n\geq 0$, with
$n\geq 0$, with ![]() $u_0=\underline{u}$ and
$u_0=\underline{u}$ and ![]() $v_0=\underline{v}$ as follows:
$v_0=\underline{v}$ as follows:
 \begin{align}
\left\{
\begin{array}{ll}
-\Delta u_{n+1}+Qu_{n+1}=\mathcal{F}^k_\lambda(x,u_n,v_n) & \text{in}~~\Omega \\
-\Delta v_{n+1}+Q v_{n+1}=\mathcal{G}^k_\mu(x,u_n,v_n) & \text{in}~~\Omega \\
u_{n+1},\,\,v_{n+1} \gt 0 & \text{in}~~\Omega \\
u_{n+1}=v_{n+1}=0 & \text{on}~~\partial\Omega.
\end{array}
\right.
\end{align}
\begin{align}
\left\{
\begin{array}{ll}
-\Delta u_{n+1}+Qu_{n+1}=\mathcal{F}^k_\lambda(x,u_n,v_n) & \text{in}~~\Omega \\
-\Delta v_{n+1}+Q v_{n+1}=\mathcal{G}^k_\mu(x,u_n,v_n) & \text{in}~~\Omega \\
u_{n+1},\,\,v_{n+1} \gt 0 & \text{in}~~\Omega \\
u_{n+1}=v_{n+1}=0 & \text{on}~~\partial\Omega.
\end{array}
\right.
\end{align} From Equation (4.1),  $(\overline{\mathcal{S}}^k_{\lambda\mu})$,
$(\overline{\mathcal{S}}^k_{\lambda\mu})$, ![]() $(\underline{\mathcal{S}}_{\lambda\mu})$ and the maximum principle, by induction, we get
$(\underline{\mathcal{S}}_{\lambda\mu})$ and the maximum principle, by induction, we get ![]() $0\leq \underline{u}\leq u_n\leq u_{n+1}\leq \overline{u}$ and
$0\leq \underline{u}\leq u_n\leq u_{n+1}\leq \overline{u}$ and ![]() $0\leq \underline{v}\leq v_n\leq v_{n+1}\leq \overline{v}$ in Ω. Thus, there are
$0\leq \underline{v}\leq v_n\leq v_{n+1}\leq \overline{v}$ in Ω. Thus, there are  $u_{\lambda\mu}^k,\,v_{\lambda\mu}^k\in C^1_0(\overline{\Omega})\cap W^{2,s}(\Omega)$ such that
$u_{\lambda\mu}^k,\,v_{\lambda\mu}^k\in C^1_0(\overline{\Omega})\cap W^{2,s}(\Omega)$ such that  $\underline{u}\leq u^k_{\lambda\mu}\leq \overline{u}$ and
$\underline{u}\leq u^k_{\lambda\mu}\leq \overline{u}$ and  $\underline{v}\leq v^k_{\lambda\mu}\leq \overline{v}$ in Ω with
$\underline{v}\leq v^k_{\lambda\mu}\leq \overline{v}$ in Ω with  $-\Delta u^k_{\lambda\mu} + Qu^k_{\lambda\mu}=\mathcal{F}^k_\lambda(x,u^k_{\lambda\mu},v^k_{\lambda\mu})$ and
$-\Delta u^k_{\lambda\mu} + Qu^k_{\lambda\mu}=\mathcal{F}^k_\lambda(x,u^k_{\lambda\mu},v^k_{\lambda\mu})$ and  $-\Delta v^k_{\lambda\mu} + Qv^k_{\lambda\mu}=\mathcal{G}^k_\mu(x,u^k_{\lambda\mu},v^k_{\lambda\mu})$ in Ω. So, we have
$-\Delta v^k_{\lambda\mu} + Qv^k_{\lambda\mu}=\mathcal{G}^k_\mu(x,u^k_{\lambda\mu},v^k_{\lambda\mu})$ in Ω. So, we have
 \begin{equation*}
-\Delta u^k_{\lambda\mu}=f_\lambda^k(x,u^k_{\lambda\mu},v^k_{\lambda\mu}) \quad \mbox{and} \quad -\Delta v^k_{\lambda\mu}=g_\mu^k(x,u^k_{\lambda\mu},v^k_{\lambda\mu}) \quad \mbox{in} \quad \Omega.
\end{equation*}
\begin{equation*}
-\Delta u^k_{\lambda\mu}=f_\lambda^k(x,u^k_{\lambda\mu},v^k_{\lambda\mu}) \quad \mbox{and} \quad -\Delta v^k_{\lambda\mu}=g_\mu^k(x,u^k_{\lambda\mu},v^k_{\lambda\mu}) \quad \mbox{in} \quad \Omega.
\end{equation*} Therefore, we have  $\|u^k_{\lambda\mu}\|$ and
$\|u^k_{\lambda\mu}\|$ and  $\|v^k_{\lambda\mu}\|$ bounded. Then, for some
$\|v^k_{\lambda\mu}\|$ bounded. Then, for some ![]() $u_{\lambda\mu},\,v_{\lambda\mu}\in H_0^1(\Omega)$,
$u_{\lambda\mu},\,v_{\lambda\mu}\in H_0^1(\Omega)$,  $u^k_{\lambda\mu}\rightharpoonup u_{\lambda\mu}$ and
$u^k_{\lambda\mu}\rightharpoonup u_{\lambda\mu}$ and  $v^k_{\lambda\mu}\rightharpoonup v_{\lambda\mu}$ weakly in
$v^k_{\lambda\mu}\rightharpoonup v_{\lambda\mu}$ weakly in ![]() $H_0^1(\Omega)$ when
$H_0^1(\Omega)$ when ![]() $k\rightarrow+\infty$. Up to a subsequence, we have
$k\rightarrow+\infty$. Up to a subsequence, we have ![]() $\underline{u}\leq u_{\lambda\mu}\leq \overline{u}$ and
$\underline{u}\leq u_{\lambda\mu}\leq \overline{u}$ and ![]() $\underline{v}\leq v_{\lambda\mu}\leq \overline{v}$ in Ω. For
$\underline{v}\leq v_{\lambda\mu}\leq \overline{v}$ in Ω. For ![]() $\varphi\in C_c^\infty(\Omega)$, we have
$\varphi\in C_c^\infty(\Omega)$, we have
 \begin{equation*}
\int_\Omega\nabla u_{\lambda\mu}\nabla\varphi=
\lim_{k\rightarrow\infty}\int_\Omega-\Delta u^k_{\lambda\mu}\varphi
= \lim_{k\rightarrow\infty}f_\lambda^k(x,u^k_{\lambda\mu},v^k_{\lambda\mu})\varphi
=\int_\Omega f_\lambda(x,u_{\lambda\mu},v_{\lambda\mu})\varphi.
\end{equation*}
\begin{equation*}
\int_\Omega\nabla u_{\lambda\mu}\nabla\varphi=
\lim_{k\rightarrow\infty}\int_\Omega-\Delta u^k_{\lambda\mu}\varphi
= \lim_{k\rightarrow\infty}f_\lambda^k(x,u^k_{\lambda\mu},v^k_{\lambda\mu})\varphi
=\int_\Omega f_\lambda(x,u_{\lambda\mu},v_{\lambda\mu})\varphi.
\end{equation*}In the same way, we have
 \begin{equation*}
\int_\Omega\nabla v_{\lambda\mu}\nabla\varphi=
\lim_{k\rightarrow\infty}\int_\Omega-\Delta v^k_{\lambda\mu}\varphi
= \lim_{k\rightarrow\infty}g_\mu^k(x,u^k_{\lambda\mu},v^k_{\lambda\mu})\varphi
=\int_\Omega g_\mu(x,u_{\lambda\mu},v_{\lambda\mu})\varphi.
\end{equation*}
\begin{equation*}
\int_\Omega\nabla v_{\lambda\mu}\nabla\varphi=
\lim_{k\rightarrow\infty}\int_\Omega-\Delta v^k_{\lambda\mu}\varphi
= \lim_{k\rightarrow\infty}g_\mu^k(x,u^k_{\lambda\mu},v^k_{\lambda\mu})\varphi
=\int_\Omega g_\mu(x,u_{\lambda\mu},v_{\lambda\mu})\varphi.
\end{equation*} So, ![]() $(u_{\lambda\mu},v_{\lambda\mu})$ are weak solutions for
$(u_{\lambda\mu},v_{\lambda\mu})$ are weak solutions for ![]() $(\mathcal{P}_i)$. Since
$(\mathcal{P}_i)$. Since ![]() ${u_{\lambda\mu},v_{\lambda\mu}\in L^\infty(\Omega)}$, from [Reference Gilbarg and Trudinger31, Theorems 7.26 and 9.15]) one has
${u_{\lambda\mu},v_{\lambda\mu}\in L^\infty(\Omega)}$, from [Reference Gilbarg and Trudinger31, Theorems 7.26 and 9.15]) one has ![]() ${u_{\lambda\mu},v_{\lambda\mu}\in C^1_0(\overline{\Omega})\cap W^{2,s}(\Omega)}$, where
${u_{\lambda\mu},v_{\lambda\mu}\in C^1_0(\overline{\Omega})\cap W^{2,s}(\Omega)}$, where ![]() $C_0^1(\overline{\Omega}):=C^1(\overline{\Omega})\cap H_0^1(\Omega)$. To finish the proof, we need to show that solutions are positive. The sub-solution
$C_0^1(\overline{\Omega}):=C^1(\overline{\Omega})\cap H_0^1(\Omega)$. To finish the proof, we need to show that solutions are positive. The sub-solution ![]() $\underline{u}$ assumes one of the forms
$\underline{u}$ assumes one of the forms ![]() $\varepsilon\varphi_{1a\Omega}$,
$\varepsilon\varphi_{1a\Omega}$, ![]() $\varepsilon\varphi_{1h}$, uɛ (see the final comments in Lemma 3.9). In the first two cases, we have
$\varepsilon\varphi_{1h}$, uɛ (see the final comments in Lemma 3.9). In the first two cases, we have ![]() $\underline{u} \gt 0$ in Ω. If
$\underline{u} \gt 0$ in Ω. If ![]() $\underline{u}=u_\varepsilon$, by Remark 3.8, we get
$\underline{u}=u_\varepsilon$, by Remark 3.8, we get ![]() $\underline{u} \gt 0$ in Ω. Similarly,
$\underline{u} \gt 0$ in Ω. Similarly, ![]() $\underline{v} \gt 0$ in Ω, therefore
$\underline{v} \gt 0$ in Ω, therefore ![]() $u_{\lambda\mu},\,v_{\lambda\mu} \gt 0$ in Ω.
$u_{\lambda\mu},\,v_{\lambda\mu} \gt 0$ in Ω.
Proof of Theorem 1.4-(ii)
We define  $(\mathcal{P}^i_{\lambda\mu})$ as the problem
$(\mathcal{P}^i_{\lambda\mu})$ as the problem ![]() $(\mathcal{P}_i)$ with λ > 0 and µ > 0. Let
$(\mathcal{P}_i)$ with λ > 0 and µ > 0. Let
 \begin{equation*}
\mathcal{O}:=\left\{(\lambda
,\mu)\in\mathbb{R}^2_+\,\,:\,\,(\mathcal{P}^i_{\lambda\mu})\,\,\mbox{has a solution}\,\right\}.
\end{equation*}
\begin{equation*}
\mathcal{O}:=\left\{(\lambda
,\mu)\in\mathbb{R}^2_+\,\,:\,\,(\mathcal{P}^i_{\lambda\mu})\,\,\mbox{has a solution}\,\right\}.
\end{equation*} By statement ![]() ${\text{(i)}}$, the set
${\text{(i)}}$, the set ![]() $\mathcal{O}$ is nonempty. Let
$\mathcal{O}$ is nonempty. Let ![]() $(\overline{\lambda},\overline{\mu})\in\mathcal{O}$ and
$(\overline{\lambda},\overline{\mu})\in\mathcal{O}$ and ![]() $(\overline{u},\overline{v})$ be some solution of
$(\overline{u},\overline{v})$ be some solution of  $(\mathcal{P}^i_{\overline{\lambda}\overline{\mu}})$. We take
$(\mathcal{P}^i_{\overline{\lambda}\overline{\mu}})$. We take ![]() $\lambda,\mu \gt 0$ in such a way that
$\lambda,\mu \gt 0$ in such a way that ![]() $0 \lt \lambda\leq\overline{\lambda}$,
$0 \lt \lambda\leq\overline{\lambda}$, ![]() $0 \lt \mu\leq\overline{\mu}$. From [Reference Brézis and Oswald13], we can set
$0 \lt \mu\leq\overline{\mu}$. From [Reference Brézis and Oswald13], we can set ![]() $u_{\lambda 0} \gt 0$ and
$u_{\lambda 0} \gt 0$ and ![]() $v_{0\mu} \gt 0$ as the unique positive solutions of
$v_{0\mu} \gt 0$ as the unique positive solutions of
 \begin{equation*}
\left\{
\begin{array}{lcl}
-\Delta u=f_\lambda(x,u,0)&\text{in}~~\Omega
\\
u=0&\text{on}~~\partial\Omega
\end{array}
\right.
\quad\quad
\left\{
\begin{array}{lcl}
-\Delta v=g_\mu(x,0,v)&\text{in}~~\Omega
\\
v=0&\text{on}~~\partial\Omega.
\end{array}
\right.
\end{equation*}
\begin{equation*}
\left\{
\begin{array}{lcl}
-\Delta u=f_\lambda(x,u,0)&\text{in}~~\Omega
\\
u=0&\text{on}~~\partial\Omega
\end{array}
\right.
\quad\quad
\left\{
\begin{array}{lcl}
-\Delta v=g_\mu(x,0,v)&\text{in}~~\Omega
\\
v=0&\text{on}~~\partial\Omega.
\end{array}
\right.
\end{equation*} From Lemma 2.1, we have ![]() $0 \lt u_{\lambda 0}\leq \overline{u}\,\,\mbox{and}\,\, 0 \lt v_{0\mu}\leq \overline{v}\,\,\mbox{in }\,\, \Omega$. We define the monotone iteration for
$0 \lt u_{\lambda 0}\leq \overline{u}\,\,\mbox{and}\,\, 0 \lt v_{0\mu}\leq \overline{v}\,\,\mbox{in }\,\, \Omega$. We define the monotone iteration for ![]() $n\geq 0$, with
$n\geq 0$, with ![]() $u_0=u_{\lambda 0}$ and
$u_0=u_{\lambda 0}$ and ![]() $v_0=v_{0\mu}$ as follows:
$v_0=v_{0\mu}$ as follows:
 \begin{align}
\left\{
\begin{array}{ll}
-\Delta u_{n+1}=f_\lambda(x,u_n,v_n)& \mbox{in}~~\Omega
\\
-\Delta v_{n+1}=g_\mu(x,u_n,v_n) & \mbox{in}~~\Omega
\\
u_{n+1},\,\,v_{n+1} \gt 0& \mbox{in}~~\Omega
\\
u_{n+1}=v_{n+1}=0&\mbox{on}~~\partial\Omega.
\end{array}
\right. \\[-24pt] \nonumber
\end{align}
\begin{align}
\left\{
\begin{array}{ll}
-\Delta u_{n+1}=f_\lambda(x,u_n,v_n)& \mbox{in}~~\Omega
\\
-\Delta v_{n+1}=g_\mu(x,u_n,v_n) & \mbox{in}~~\Omega
\\
u_{n+1},\,\,v_{n+1} \gt 0& \mbox{in}~~\Omega
\\
u_{n+1}=v_{n+1}=0&\mbox{on}~~\partial\Omega.
\end{array}
\right. \\[-24pt] \nonumber
\end{align} Since all weights ![]() $a(\cdot),b(\cdot),c(\cdot),d(\cdot)$ are nonnegative, as in statement (i), by the maximum principle and induction on
$a(\cdot),b(\cdot),c(\cdot),d(\cdot)$ are nonnegative, as in statement (i), by the maximum principle and induction on ![]() $n\geq 0$, we get
$n\geq 0$, we get ![]() $0 \lt u_{\lambda 0}\leq u_n\leq u_{n+1}\leq\overline{u}$ and
$0 \lt u_{\lambda 0}\leq u_n\leq u_{n+1}\leq\overline{u}$ and ![]() $0 \lt v_{0\mu}\leq v_n\leq v_{n+1}\leq\overline{v}$ in Ω. Then,
$0 \lt v_{0\mu}\leq v_n\leq v_{n+1}\leq\overline{v}$ in Ω. Then, ![]() $(u_n,v_n)$ converge strongly in
$(u_n,v_n)$ converge strongly in ![]() $H_0^1\times H_0^1$ to some solution
$H_0^1\times H_0^1$ to some solution ![]() $(u_{\lambda\mu},v_{\lambda\mu})$ of
$(u_{\lambda\mu},v_{\lambda\mu})$ of  $(\mathcal{P}^i_{\lambda\mu})$. Furthermore,
$(\mathcal{P}^i_{\lambda\mu})$. Furthermore, ![]() $0 \lt u_{\lambda 0}\leq u_{\lambda\mu}\leq\overline{u}$ and
$0 \lt u_{\lambda 0}\leq u_{\lambda\mu}\leq\overline{u}$ and ![]() $0 \lt v_{0\mu}\leq v_{\lambda\mu}\leq\overline{v}$, so this solution is a minimal positive solution as defined in Equation (1.3).
$0 \lt v_{0\mu}\leq v_{\lambda\mu}\leq\overline{v}$, so this solution is a minimal positive solution as defined in Equation (1.3).
If ![]() $(\widetilde{u},\widetilde{v})$ is a solution of
$(\widetilde{u},\widetilde{v})$ is a solution of  $(\mathcal{P}^i_{\lambda\mu})$, by Lemma 2.1, we have
$(\mathcal{P}^i_{\lambda\mu})$, by Lemma 2.1, we have ![]() $0 \lt u_{\lambda 0}\leq \widetilde{u}\,\,\mbox{and}\,\, 0 \lt v_{0\mu}\leq \widetilde{v}\,\,\mbox{in }\,\, \Omega$. Therefore,
$0 \lt u_{\lambda 0}\leq \widetilde{u}\,\,\mbox{and}\,\, 0 \lt v_{0\mu}\leq \widetilde{v}\,\,\mbox{in }\,\, \Omega$. Therefore, ![]() $0 \lt u_{\lambda 0}\leq u_n\leq \widetilde{u}\,\,\mbox{and}\,\, 0 \lt v_{0\mu}\leq v_n\leq \widetilde{v}\,\,\mbox{in }\,\, \Omega$, and so we get
$0 \lt u_{\lambda 0}\leq u_n\leq \widetilde{u}\,\,\mbox{and}\,\, 0 \lt v_{0\mu}\leq v_n\leq \widetilde{v}\,\,\mbox{in }\,\, \Omega$, and so we get ![]() $u_{\lambda\mu}\leq \widetilde{u}$ and
$u_{\lambda\mu}\leq \widetilde{u}$ and ![]() $v_{\lambda\mu}\leq \widetilde{v}$. In this way, we prove the existence of minimal solutions for all
$v_{\lambda\mu}\leq \widetilde{v}$. In this way, we prove the existence of minimal solutions for all ![]() $(\lambda,\mu)\in\mathcal{O}$ and
$(\lambda,\mu)\in\mathcal{O}$ and ![]() $(0,\lambda]\times(0,\mu]\subset\mathcal{O}$. Now we define
$(0,\lambda]\times(0,\mu]\subset\mathcal{O}$. Now we define ![]() $\mathcal{O}_1:=\left\{\lambda \gt 0\,\,:\,\,\mbox{for some}\,\,\mu \gt 0\,\,\mbox{we have }\,\,(\lambda,\mu)\in\mathcal{O}\right\}$. From the last observation,
$\mathcal{O}_1:=\left\{\lambda \gt 0\,\,:\,\,\mbox{for some}\,\,\mu \gt 0\,\,\mbox{we have }\,\,(\lambda,\mu)\in\mathcal{O}\right\}$. From the last observation, ![]() $\mathcal{O}_1$ is a nonempty interval. Let
$\mathcal{O}_1$ is a nonempty interval. Let ![]() $L_{ij}^*:=\sup\mathcal{O}_1$. From statement (i), we see that
$L_{ij}^*:=\sup\mathcal{O}_1$. From statement (i), we see that ![]() $L_{ij}^*=+\infty$ if and only if
$L_{ij}^*=+\infty$ if and only if ![]() $\sigma_{ij} \gt 0$ and
$\sigma_{ij} \gt 0$ and ![]() $\overline{\sigma}_{ij} \gt 0$, which only holds when
$\overline{\sigma}_{ij} \gt 0$, which only holds when ![]() $i=j=1$ and
$i=j=1$ and ![]() $i=j=2$. Taking
$i=j=2$. Taking ![]() $\lambda\in (0,L_{ij}^*)$, we set the nonempty interval
$\lambda\in (0,L_{ij}^*)$, we set the nonempty interval ![]() $\mathcal{O}_\lambda=\left\{\mu \gt 0\,\,:\,\,(\lambda,\mu)\in\mathcal{O}\right\}$ and
$\mathcal{O}_\lambda=\left\{\mu \gt 0\,\,:\,\,(\lambda,\mu)\in\mathcal{O}\right\}$ and ![]() $\Lambda_\lambda:=\sup\mathcal{O}_\lambda$. From Theorem 1.2,
$\Lambda_\lambda:=\sup\mathcal{O}_\lambda$. From Theorem 1.2, ![]() $\Lambda_\lambda \lt +\infty$, and this ends the proof of
$\Lambda_\lambda \lt +\infty$, and this ends the proof of ![]() ${(ii)}$.
${(ii)}$.
If ![]() $(\widetilde{u},\widetilde{v})$ is a solution of
$(\widetilde{u},\widetilde{v})$ is a solution of  $(\mathcal{P}^i_{\lambda\mu})$, by Lemma 2.1, we have
$(\mathcal{P}^i_{\lambda\mu})$, by Lemma 2.1, we have ![]() $0 \lt u_{\lambda 0}\leq \widetilde{u}\,\,\mbox{and}\,\, 0 \lt v_{0\mu}\leq \widetilde{v}\,\,\mbox{in }\,\, \Omega$. Therefore,
$0 \lt u_{\lambda 0}\leq \widetilde{u}\,\,\mbox{and}\,\, 0 \lt v_{0\mu}\leq \widetilde{v}\,\,\mbox{in }\,\, \Omega$. Therefore, ![]() $0 \lt u_{\lambda 0}\leq u_n\leq \widetilde{u}\,\,\mbox{and}\,\, 0 \lt v_{0\mu}\leq v_n\leq \widetilde{v}\,\,\mbox{in }\,\, \Omega$, and so we get
$0 \lt u_{\lambda 0}\leq u_n\leq \widetilde{u}\,\,\mbox{and}\,\, 0 \lt v_{0\mu}\leq v_n\leq \widetilde{v}\,\,\mbox{in }\,\, \Omega$, and so we get ![]() $u_{\lambda\mu}\leq \widetilde{u}$ and
$u_{\lambda\mu}\leq \widetilde{u}$ and ![]() $v_{\lambda\mu}\leq \widetilde{v}$. In this way, we prove the existence of minimal solutions for all
$v_{\lambda\mu}\leq \widetilde{v}$. In this way, we prove the existence of minimal solutions for all ![]() $(\lambda,\mu)\in\mathcal{O}$ and
$(\lambda,\mu)\in\mathcal{O}$ and ![]() $(0,\lambda]\times(0,\mu]\subset\mathcal{O}$. Now we define
$(0,\lambda]\times(0,\mu]\subset\mathcal{O}$. Now we define ![]() $\mathcal{O}_1:=\left\{\lambda \gt 0\,\,:\,\,\mbox{for some}\,\,\mu \gt 0\,\,\mbox{we have }\,\,(\lambda,\mu)\in\mathcal{O}\right\}$. From the last observation,
$\mathcal{O}_1:=\left\{\lambda \gt 0\,\,:\,\,\mbox{for some}\,\,\mu \gt 0\,\,\mbox{we have }\,\,(\lambda,\mu)\in\mathcal{O}\right\}$. From the last observation, ![]() $\mathcal{O}_1$ is a nonempty interval. Let
$\mathcal{O}_1$ is a nonempty interval. Let ![]() $L_{ij}^*:=\sup\mathcal{O}_1$. From statement (i), we see that
$L_{ij}^*:=\sup\mathcal{O}_1$. From statement (i), we see that ![]() $L_{ij}^*=+\infty$ if and only if
$L_{ij}^*=+\infty$ if and only if ![]() $\sigma_{ij} \gt 0$ and
$\sigma_{ij} \gt 0$ and ![]() $\overline{\sigma}_{ij} \gt 0$, which only holds when
$\overline{\sigma}_{ij} \gt 0$, which only holds when ![]() $i=j=1$ and
$i=j=1$ and ![]() $i=j=2$. Taking
$i=j=2$. Taking ![]() $\lambda\in (0,L_{ij}^*)$, we set the nonempty interval
$\lambda\in (0,L_{ij}^*)$, we set the nonempty interval ![]() $\mathcal{O}_\lambda=\left\{\mu \gt 0\,\,:\,\,(\lambda,\mu)\in\mathcal{O}\right\}$ and
$\mathcal{O}_\lambda=\left\{\mu \gt 0\,\,:\,\,(\lambda,\mu)\in\mathcal{O}\right\}$ and ![]() $\Lambda_\lambda:=\sup\mathcal{O}_\lambda$. From Theorem 1.2,
$\Lambda_\lambda:=\sup\mathcal{O}_\lambda$. From Theorem 1.2, ![]() $\Lambda_\lambda \lt +\infty$, and this ends the proof of
$\Lambda_\lambda \lt +\infty$, and this ends the proof of ![]() ${(ii)}$.
${(ii)}$.
Proof of Theorem 1.4-(iii) and (iv)
Follows immediately from ![]() ${(ii)}$.
${(ii)}$.
Proof of Theorem 1.4-(v)
The proof of the existence of a solution to ![]() $0 \lt \lambda \lt L^*_{ij}$ and
$0 \lt \lambda \lt L^*_{ij}$ and ![]() $\mu = \Lambda_\lambda$ is similar to the proof of [Reference Ambrosetti, Brézis and Cerami4, Lemma 3.5]. We will only deal with the case related to the system
$\mu = \Lambda_\lambda$ is similar to the proof of [Reference Ambrosetti, Brézis and Cerami4, Lemma 3.5]. We will only deal with the case related to the system ![]() $(\mathcal{P}_i)$ with i = 1, as the case i = 2 is quite similar. We will do a very short proof. For all λ > 0 and
$(\mathcal{P}_i)$ with i = 1, as the case i = 2 is quite similar. We will do a very short proof. For all λ > 0 and ![]() $\mu \lt \Lambda_\lambda$, we define
$\mu \lt \Lambda_\lambda$, we define  $A_{\lambda\mu}(x) = \lambda a(x)u_{\lambda\mu}^{q-1} + \alpha c(x)u_{\lambda\mu}^{\alpha-1} v_{\lambda\mu}^\beta$. Despite the fact that the possibility of
$A_{\lambda\mu}(x) = \lambda a(x)u_{\lambda\mu}^{q-1} + \alpha c(x)u_{\lambda\mu}^{\alpha-1} v_{\lambda\mu}^\beta$. Despite the fact that the possibility of ![]() $A_{\lambda\mu}(x) = +\infty$ for some values
$A_{\lambda\mu}(x) = +\infty$ for some values ![]() $x \in \partial\Omega$, the spectral theory for
$x \in \partial\Omega$, the spectral theory for ![]() $-\Delta-A_{\lambda\mu}(x)$ can still be carried over in
$-\Delta-A_{\lambda\mu}(x)$ can still be carried over in ![]() $H_0^1(\Omega)$ (see [Reference Ambrosetti, Brézis and Cerami4, Remark 2.1]). We claim that ν 1, the first eigenvalue of
$H_0^1(\Omega)$ (see [Reference Ambrosetti, Brézis and Cerami4, Remark 2.1]). We claim that ν 1, the first eigenvalue of ![]() $\mathcal{(LP)}$, is nonnegative.
$\mathcal{(LP)}$, is nonnegative.
 \begin{align}
\left\{
\begin{array}{ll}
-\Delta \phi-A_{\lambda\mu}(x)\phi=\nu\phi & \mbox{in}~~\Omega
\\
\phi=0&\mbox{on}~~\partial\Omega.
\end{array}
\right.
\end{align}
\begin{align}
\left\{
\begin{array}{ll}
-\Delta \phi-A_{\lambda\mu}(x)\phi=\nu\phi & \mbox{in}~~\Omega
\\
\phi=0&\mbox{on}~~\partial\Omega.
\end{array}
\right.
\end{align} In fact, suppose that ![]() $\nu_1 \lt 0$, and let
$\nu_1 \lt 0$, and let ![]() $\phi_1 \gt 0$ be the first eigenfunction of
$\phi_1 \gt 0$ be the first eigenfunction of ![]() $\mathcal{(LP)}$. Following the proof of Lemma 3.5 in [Reference Ambrosetti, Brézis and Cerami4, p. 528], we obtain for a small ɛ > 0:
$\mathcal{(LP)}$. Following the proof of Lemma 3.5 in [Reference Ambrosetti, Brézis and Cerami4, p. 528], we obtain for a small ɛ > 0:
On the other hand, we have:
Then, ![]() $(u_{\lambda\mu}-\varepsilon\phi_1,v_{\lambda\mu})$ satisfies
$(u_{\lambda\mu}-\varepsilon\phi_1,v_{\lambda\mu})$ satisfies ![]() $(\overline{\mathcal{S}}_{\lambda\mu})$. The iteration
$(\overline{\mathcal{S}}_{\lambda\mu})$. The iteration ![]() $(\mathcal{P}^n_{\lambda\mu})$ gives us:
$(\mathcal{P}^n_{\lambda\mu})$ gives us:
which is not possible because ![]() $\phi_1 \gt 0$. Therefore, we have
$\phi_1 \gt 0$. Therefore, we have ![]() $\nu_1\geq 0$. From
$\nu_1\geq 0$. From ![]() $(\mathcal{LP})$ we get:
$(\mathcal{LP})$ we get:
 \begin{equation*}
\int_\Omega |\nabla \phi|^2-A_{\lambda\mu}(x)\phi^2 \geq 0,\,\,\,\forall\phi\in H_0^1(\Omega).
\end{equation*}
\begin{equation*}
\int_\Omega |\nabla \phi|^2-A_{\lambda\mu}(x)\phi^2 \geq 0,\,\,\,\forall\phi\in H_0^1(\Omega).
\end{equation*} Taking ![]() $\phi=u_{\lambda\mu}$, we get:
$\phi=u_{\lambda\mu}$, we get:
 \begin{equation}
\|u_{\lambda\mu}\|^2 \geq \lambda q\int_\Omega a(x)u_{\lambda\mu}^{q+1}+\alpha \int_\Omega c(x)u_{\lambda\mu}^{\alpha+1}v_{\lambda\mu}^\beta.
\end{equation}
\begin{equation}
\|u_{\lambda\mu}\|^2 \geq \lambda q\int_\Omega a(x)u_{\lambda\mu}^{q+1}+\alpha \int_\Omega c(x)u_{\lambda\mu}^{\alpha+1}v_{\lambda\mu}^\beta.
\end{equation} Since ![]() $(u_{\lambda\mu},v_{\lambda\mu})$ is a solution to
$(u_{\lambda\mu},v_{\lambda\mu})$ is a solution to  $(\mathcal{P}^i_{\lambda\mu})$, we have
$(\mathcal{P}^i_{\lambda\mu})$, we have
 \begin{equation}
\|u_{\lambda\mu}\|^2= \lambda \int_\Omega a(x)u_{\lambda\mu}^{q+1}+
\int_\Omega c(x)u_{\lambda\mu}^{\alpha+1}v_{\lambda\mu}^\beta.
\end{equation}
\begin{equation}
\|u_{\lambda\mu}\|^2= \lambda \int_\Omega a(x)u_{\lambda\mu}^{q+1}+
\int_\Omega c(x)u_{\lambda\mu}^{\alpha+1}v_{\lambda\mu}^\beta.
\end{equation} Everything we have done so far works for the case ![]() $0 \lt \alpha\leq 1$. The only moment that we have used α > 1 is now. By Equations (4.2) and (4.3), we get
$0 \lt \alpha\leq 1$. The only moment that we have used α > 1 is now. By Equations (4.2) and (4.3), we get
 \begin{equation*}
\|u_{\lambda\mu}\|^2\leq\lambda\left(\dfrac{\alpha-p}{\alpha-1}\right)\int_\Omega a(x)u_{\lambda\mu}^{q+1}.
\end{equation*}
\begin{equation*}
\|u_{\lambda\mu}\|^2\leq\lambda\left(\dfrac{\alpha-p}{\alpha-1}\right)\int_\Omega a(x)u_{\lambda\mu}^{q+1}.
\end{equation*} Then for some ![]() $C_q \gt 0$, we have
$C_q \gt 0$, we have
 \begin{equation}
\|u_{\lambda\mu}\|^{1-q}\leq \lambda C_q\left(\dfrac{\alpha-q}{\alpha-1}\right).
\end{equation}
\begin{equation}
\|u_{\lambda\mu}\|^{1-q}\leq \lambda C_q\left(\dfrac{\alpha-q}{\alpha-1}\right).
\end{equation} In the same way, if γ > 1 we get for some ![]() $C_p \gt 0$
$C_p \gt 0$
 \begin{equation}
\|v_{\lambda\mu}\|^{1-p}\leq \mu C_p\left(\dfrac{\gamma-p}{\gamma-1}\right).
\end{equation}
\begin{equation}
\|v_{\lambda\mu}\|^{1-p}\leq \mu C_p\left(\dfrac{\gamma-p}{\gamma-1}\right).
\end{equation} Now we will prove the existence of a solution for the case λ > 0 and ![]() $\mu=\Lambda_\lambda$. In order to do this, we take a sequence
$\mu=\Lambda_\lambda$. In order to do this, we take a sequence ![]() $\mu_n \lt \mu_{n+1} \lt \Lambda_\lambda$ such that
$\mu_n \lt \mu_{n+1} \lt \Lambda_\lambda$ such that ![]() $\mu_n\rightarrow\Lambda_\lambda$. We define
$\mu_n\rightarrow\Lambda_\lambda$. We define ![]() $u_n=u_{\lambda\mu_n}$ and
$u_n=u_{\lambda\mu_n}$ and ![]() $v_n=v_{\lambda\mu_n}$ as the minimal solutions for
$v_n=v_{\lambda\mu_n}$ as the minimal solutions for  $(\mathcal{P}^i_{\lambda\mu_n})$. Moreover, we have
$(\mathcal{P}^i_{\lambda\mu_n})$. Moreover, we have
Since α > 1 and γ > 1, by Equations (4.4) and (4.5), we have that un and vn are bounded in ![]() $H_0^1(\Omega)$. Then, we have for some
$H_0^1(\Omega)$. Then, we have for some ![]() $u,\,v\in H_0^1(\Omega)$,
$u,\,v\in H_0^1(\Omega)$,
From Equation (4.6), we get
 \begin{equation}
u_n\leq u=\lim_{n\rightarrow\infty}u_n\,\,\,\,\mbox{and}\,\,\,\,v_n\leq v=\lim_{n\rightarrow\infty}v_n.
\end{equation}
\begin{equation}
u_n\leq u=\lim_{n\rightarrow\infty}u_n\,\,\,\,\mbox{and}\,\,\,\,v_n\leq v=\lim_{n\rightarrow\infty}v_n.
\end{equation}It is not hard to see that
 \begin{equation}
\left\{
\begin{array}{lcll}
\displaystyle\lim_{n\rightarrow+\infty}\int_\Omega c(x)u_n^\alpha v_n^\beta\varphi&=&
\displaystyle\int_\Omega c(x)u^\alpha v^\beta\varphi,&\forall \varphi\in C_c^\infty(\Omega)
\\[12pt]
\displaystyle\lim_{n\rightarrow+\infty}\int_\Omega d(x)u_n^\theta v_n^\gamma\varphi&=&
\displaystyle\int_\Omega d(x)u^\theta v^\gamma\varphi,&\forall \varphi\in C_c^\infty(\Omega).
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{lcll}
\displaystyle\lim_{n\rightarrow+\infty}\int_\Omega c(x)u_n^\alpha v_n^\beta\varphi&=&
\displaystyle\int_\Omega c(x)u^\alpha v^\beta\varphi,&\forall \varphi\in C_c^\infty(\Omega)
\\[12pt]
\displaystyle\lim_{n\rightarrow+\infty}\int_\Omega d(x)u_n^\theta v_n^\gamma\varphi&=&
\displaystyle\int_\Omega d(x)u^\theta v^\gamma\varphi,&\forall \varphi\in C_c^\infty(\Omega).
\end{array}
\right.
\end{equation} Since ![]() $(u_n,v_n)$ is a solution for
$(u_n,v_n)$ is a solution for  $(\mathcal{P}^i_{\lambda\mu_n})$ and
$(\mathcal{P}^i_{\lambda\mu_n})$ and ![]() $\mu_n\rightarrow\Lambda_\lambda$, by Equations (4.6)–(4.9), we have that (u, v) is a weak solution for
$\mu_n\rightarrow\Lambda_\lambda$, by Equations (4.6)–(4.9), we have that (u, v) is a weak solution for  $(\mathcal{P}^i_{\lambda\mu})$ with
$(\mathcal{P}^i_{\lambda\mu})$ with ![]() $0 \lt \lambda \lt L^*_{ij}$ and
$0 \lt \lambda \lt L^*_{ij}$ and ![]() $\mu=\Lambda_\lambda$. The other case is similar.
$\mu=\Lambda_\lambda$. The other case is similar.
Acknowledgements
The author is grateful to the anonymous referee for her/his comments and suggestions, which contributed significantly to improving the manuscript’s quality.
Funding Statement
The author was partially supported by CNPq/Brazil 104432/2020-9 and FAP-DF/Brazil 00193-00001820/2022-86.