A real variety whose real locus achieves the Smith–Thom equality is called maximal. This paper introduces new constructions of maximal real varieties, by using moduli spaces of geometric objects. We establish the maximality of the following real varieties:

• – moduli spaces of stable vector bundles of coprime rank and degree over a maximal real curve (recovering Brugallé–Schaffhauser’s theorem with a short new proof), which extends to moduli spaces of parabolic vector bundles;

• – moduli spaces of stable Higgs bundles of coprime rank and degree over a maximal real curve, providing maximal hyper-Kähler manifolds in every even dimension;

• – if a real variety has maximal Hilbert square, then the variety and its Hilbert cube are maximal, which happens for all maximal real cubic 3-folds, but never for maximal real cubic 4-folds;

• – punctual Hilbert schemes on a maximal real surface with vanishing first 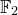$\mathbb {F}_2$-Betti number and connected real locus, such as 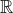$\mathbb {R}$-rational maximal real surfaces and some generalized Dolgachev surfaces;

• – moduli spaces of stable sheaves on an 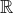$\mathbb {R}$-rational maximal Poisson surface (e.g. the real projective plane).